苏科版数学七下9.2单项式乘多项式(共17张PPT)
文档属性
| 名称 | 苏科版数学七下9.2单项式乘多项式(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 350.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-12 16:11:36 | ||
图片预览



文档简介
(共17张PPT)
9.2单项式乘多项式
1.根据单项式乘单项式的法则填空:
2.已知3xn-3y5-n与-8x3my2n的积
是2x4y9的同类项,求m、n的值.
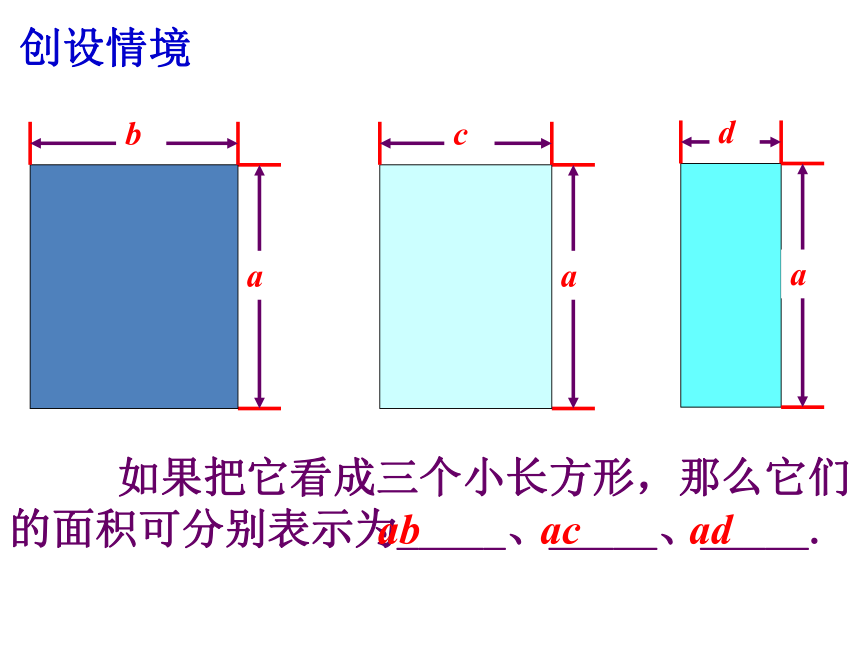
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
a
a
b
c
a
d
ab
ad
ac
创设情境
a
a
b
c
a
d
d
c
b
a
d
c
b
a
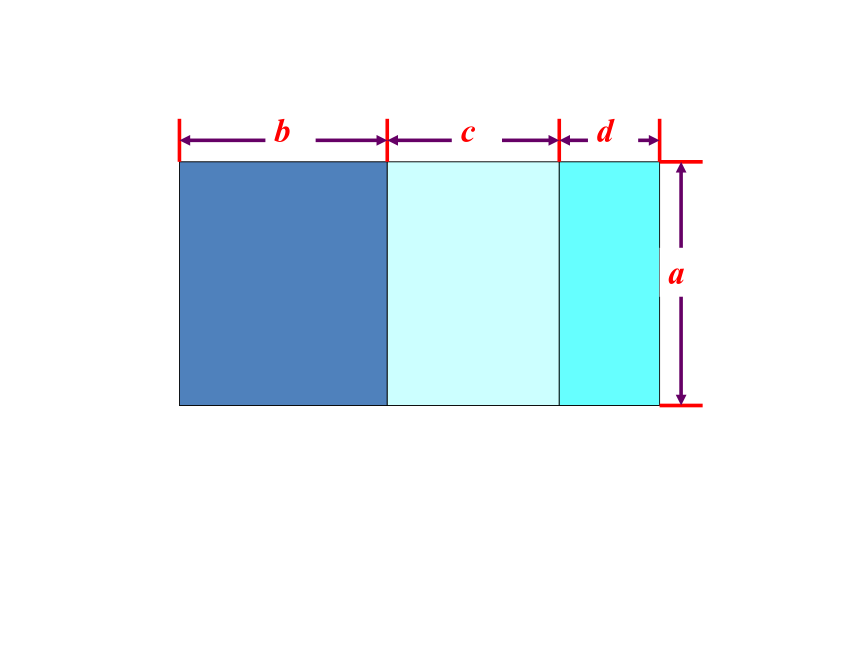
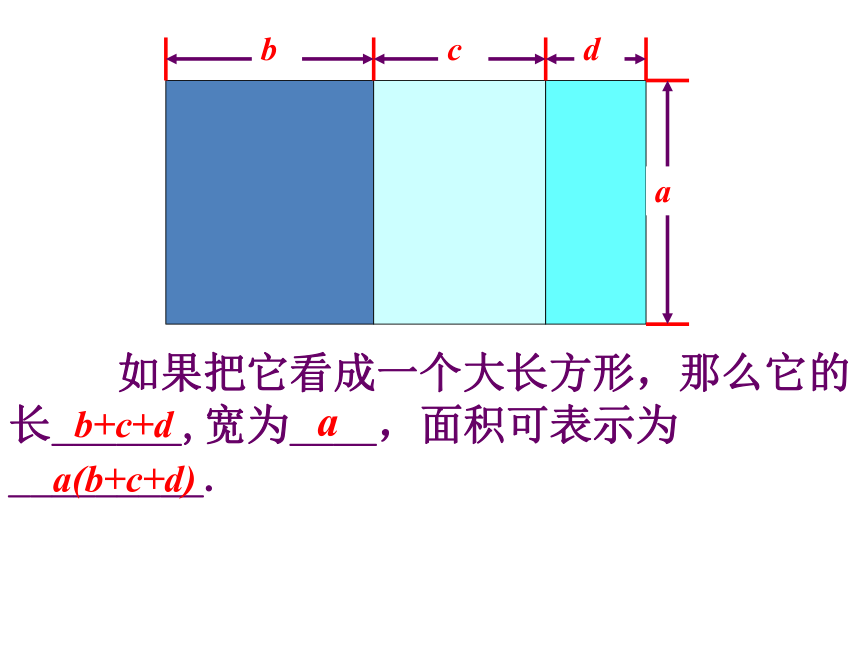
如果把它看成一个大长方形,那么它的长______,宽为____,面积可表示为_________.
b+c+d
a(b+c+d)
a
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
如果把它看成一个大长方形,那么它的面积可表示为_________.
d
c
b
a
ab
ad
ac
a(b+c+d)
ab+ac+ad
a(b+c+d)
ab+ac+ad
a(b+c+d)
a(b+c+d)
ac
+
ad
ab
+
根据乘法的分配律
如何计算下列各式,请说明理由。
(1)a(5a+3b)
(2)(x-2y)·2x
做一做
如何进行单项式乘多项式的乘法运算?
单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.
单项式乘多项式的运算法则
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.
例1 计算:
(1) (-3x2)·(4x-3)
(2)
(3)
(4)
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
例2:如图:一块长方形地用来建造住宅、广场、商厦,求这块地的面积.
4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab
答:这块地的面积为20a2+4ab.
完成书P70练一练
例3.
其中y=-3,n=2
2. 已知:xy2=-6,求-xy(x3y7-3x2y5-y)
1.已知:xy2=-2,求-xy(x3y7-3x2y5-y)
思考:要使
的结果中不含
项,则
等于多少?
知识延伸
知识延伸
3.已知M,N分别表示不同的单项式,且3x(M-5x)=6x2y3+N,求M,N.
2.已知A=-3xy2,B=2xy(x-y),求A·B
1.单项式与多项式相乘的依据是乘法对加法的分配律.
2.单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项.
3.积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意运用去括号法则.
9.2单项式乘多项式
1.根据单项式乘单项式的法则填空:
2.已知3xn-3y5-n与-8x3my2n的积
是2x4y9的同类项,求m、n的值.
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
a
a
b
c
a
d
ab
ad
ac
创设情境
a
a
b
c
a
d
d
c
b
a
d
c
b
a
如果把它看成一个大长方形,那么它的长______,宽为____,面积可表示为_________.
b+c+d
a(b+c+d)
a
如果把它看成三个小长方形,那么它们的面积可分别表示为_____、_____、_____.
如果把它看成一个大长方形,那么它的面积可表示为_________.
d
c
b
a
ab
ad
ac
a(b+c+d)
ab+ac+ad
a(b+c+d)
ab+ac+ad
a(b+c+d)
a(b+c+d)
ac
+
ad
ab
+
根据乘法的分配律
如何计算下列各式,请说明理由。
(1)a(5a+3b)
(2)(x-2y)·2x
做一做
如何进行单项式乘多项式的乘法运算?
单项式与多项式相乘,就是依据乘法分配律,用单项式乘多项式的每一项,再把所得的积相加.
单项式乘多项式的运算法则
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加.
例1 计算:
(1) (-3x2)·(4x-3)
(2)
(3)
(4)
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
例2:如图:一块长方形地用来建造住宅、广场、商厦,求这块地的面积.
4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab
答:这块地的面积为20a2+4ab.
完成书P70练一练
例3.
其中y=-3,n=2
2. 已知:xy2=-6,求-xy(x3y7-3x2y5-y)
1.已知:xy2=-2,求-xy(x3y7-3x2y5-y)
思考:要使
的结果中不含
项,则
等于多少?
知识延伸
知识延伸
3.已知M,N分别表示不同的单项式,且3x(M-5x)=6x2y3+N,求M,N.
2.已知A=-3xy2,B=2xy(x-y),求A·B
1.单项式与多项式相乘的依据是乘法对加法的分配律.
2.单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数相同,注意不要漏乘项.
3.积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意运用去括号法则.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
