4.3探索三角形全等的条件(用“边角边”判定三角形全等)课件(共17张PPT) 2024-2025学年北师大版七年级数学下册
文档属性
| 名称 | 4.3探索三角形全等的条件(用“边角边”判定三角形全等)课件(共17张PPT) 2024-2025学年北师大版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-19 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
第四章 三角形
4.3.3 探索三角形全等的条件
(第3课时)用“边角边”判定三角形全等
1.理解并掌握三角形全等判定“边角边”条件的内容并增强学生的探索 能力.(重点)
2.熟练利用“边角边”条件证明两个三角形全等及理解边边角不能判定三 角形全等。(难点)
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
目标学习
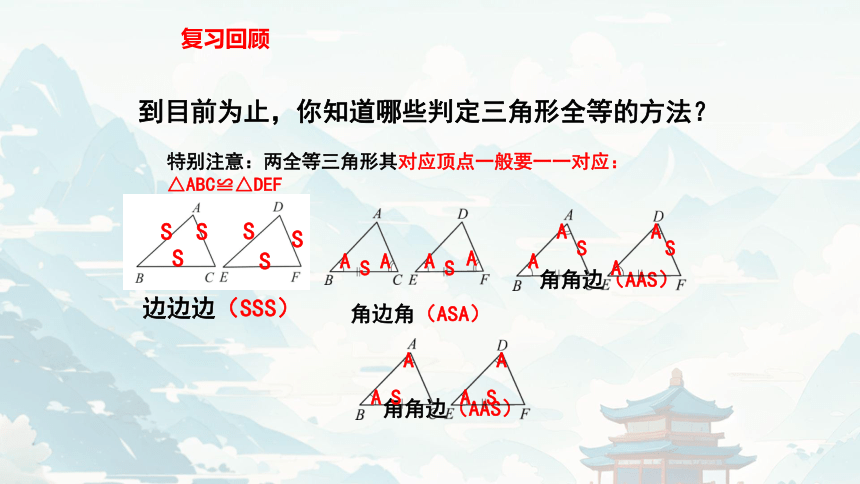
到目前为止,你知道哪些判定三角形全等的方法?
边边边(SSS)
复习回顾
S
S
S
S
S
S
角边角(ASA)
A
A
S
S
A
A
角角边(AAS)
A
A
A
A
S
S
角角边(AAS)
A
A
A
A
S
S
特别注意:两全等三角形其对应顶点一般要一一对应:△ABC≌△DEF
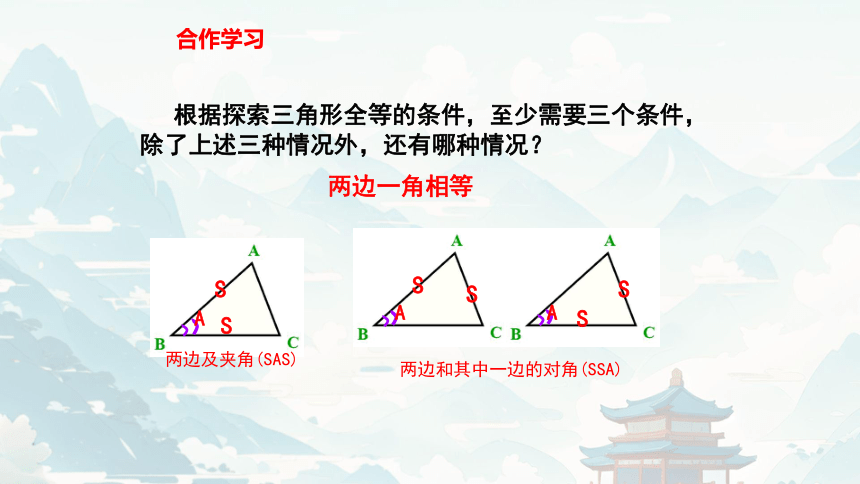
根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?
两边一角相等
合作学习
两边及夹角(SAS)
S
A
S
两边和其中一边的对角(SSA)
S
S
A
S
S
A
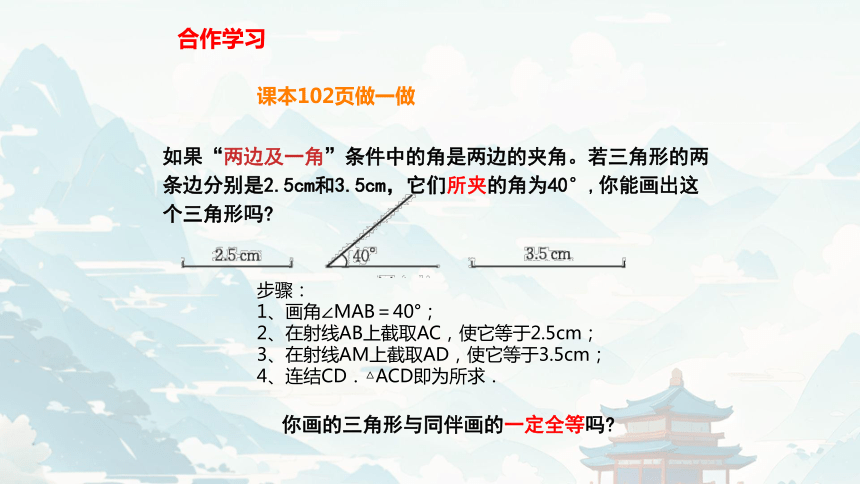
如果“两边及一角”条件中的角是两边的夹角。若三角形的两条边分别是2.5cm和3.5cm,它们所夹的角为40°,你能画出这个三角形吗
你画的三角形与同伴画的一定全等吗
课本102页做一做
合作学习
步骤:
1、画角∠MAB=40°;
2、在射线AB上截取AC,使它等于2.5cm;
3、在射线AM上截取AD,使它等于3.5cm;
4、连结CD.△ACD即为所求.
合作学习
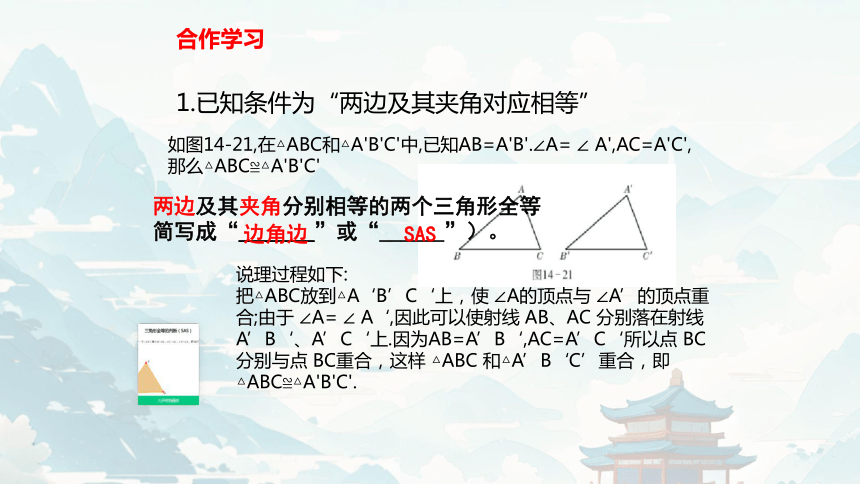
1.已知条件为“两边及其夹角对应相等”
如图14-21,在△ABC和△A'B'C'中,已知AB=A'B'.∠A= ∠ A',AC=A'C',那么△ABC≌△A'B'C'
说理过程如下:
把△ABC放到△A‘B’C‘上,使 ∠A的顶点与 ∠A’的顶点重合;由于 ∠A= ∠ A‘,因此可以使射线 AB、AC 分别落在射线A’B‘、A’C‘上.因为AB=A’B‘,AC=A’C‘所以点 BC分别与点 BC重合,这样 △ABC 和△A’B‘C’重合,即△ABC≌△A'B'C'.
两边及其夹角分别相等的两个三角形全等
简写成“_______”或“______”)。
边角边
SAS
合作学习
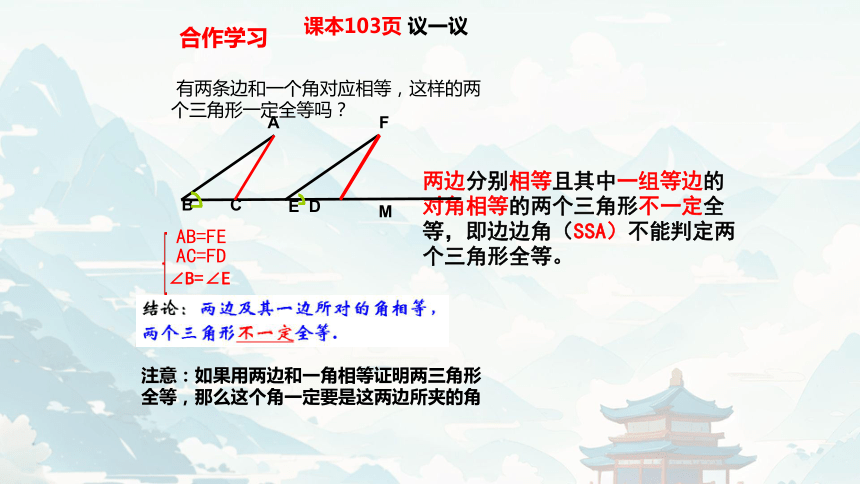
课本103页 议一议
两边分别相等且其中一组等边的对角相等的两个三角形不一定全等,即边边角(SSA)不能判定两个三角形全等。
有两条边和一个角对应相等,这样的两个三角形一定全等吗?
注意:如果用两边和一角相等证明两三角形全等,那么这个角一定要是这两边所夹的角
B
A
C
E
F
D
AB=FE
AC=FD
∠B=∠E
M
两边及其夹角分别相等的两个三角形全等
简写成“_______”或“______”)。
边角边
SAS
总结归纳
课本103页
几何语言
请在课本103页上书写
在△ABC 和△DEF中
AB=DE
S
S
∠B=∠E
A
A
BC=EF
S
S
∴△ABC ≌△DEF
(SAS)
特别注意:两三角形全等其对应顶点一般要一一对应:△ABC≌△DEF
特别注意: 两边分别相等且其中一组等边的对角相等的两个三角形不一定全等,即边边角(SSA)不能判定两个三角形全等。
例题学习
零障碍82页例1
(对顶角相等)
(SAS)
S
S
(已知)
A
A
S
S
(已知)
随堂练习
1.在下列图中找出全等三角形,并把它们用线连起来.
5cm
5cm
)
⑼
)
5cm
5cm
35°
⑴
35°
)
⑺
3cm
4cm
)
⑵
3cm
4cm
⑹
6cm
5cm
⑸
2cm
3cm
⑶
5cm
4cm
⑻
2cm
5cm
⑽
4cm
5cm
⑷
4cm
3cm
随堂练习
2.小明做了一个如图所示的风筝,其中∠ 1=∠2,ED=FD,将上述条件标注在图 中,小明不用测量就能知道EH=FH吗?与同伴 进行交流.
解:是,理由如下:
∵在△EDH和△FDH中
ED=FD(已知)
∠1=∠2(已知)
DH=DH(公共边)
∴△DEH≌△DFH(SAS)
∴EH=FH(全等三角形的对应边相等)
)
)
1
2
随堂练习
3.如图,已知AB=AC,AD=AE
能说明△BOE≌△COD吗?为什么?
解:在△ABD和△ACE中
AB=AC(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴△ABD≌△ACE(SAS)
∴∠B=∠C
(全等三角形对应角相等)
随堂练习
4.如图,两个三角形绕点A旋转,已知AB=AD,AC=AE,∠1=∠2,
试说明:BC=DE.
解:∵∠1= ∠2
∴ ∠1+ ∠ EAC=∠2 +∠EAC
即∠ BAC=∠DAE
在△ABC和△ADE中
AB=AD
∠ BAC=∠DAE
AC=AE
∴△ABC≌△ADE(SAS)
∴BC=DE(全等三角形的对应边相等)
)
)
1
2
随堂练习
5.两个三角形绕点A旋转至如图所示位置若AB=AD,AC=AE,∠BAE=∠DAE,
试说明:BC=DE.
∴△ABC≌△ADE(SAS)
∴BC=DE(全等三角形的对应边相等).
解:∵ ∠BAE=∠DAE
∴ ∠BAE -∠ EAC=∠DAE -∠EAC
即∠ 1=∠2
在△ABC和△ADE中
AB=AD
∠ 1=∠2
AC=AE
随堂练习
6.如图,已知AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,试说明:BQ=CP.
解:∵ ∠QAP=∠BAC(已知)
∴ ∠QAP-∠BAP=∠BAC-∠BAP
∴∠1=∠2(等式性质)
在△ABQ和△ACP中
AB=AC(已知)
∵ ∠1=∠2(已证)
AQ=QP(已知)
∴ △ABQ≌△ACP(SAS)
∴BQ=CP(全等三角形对应边相等)
1
2
课堂总结
课堂总结
课本P104
习题4.8
第四章 三角形
4.3.3 探索三角形全等的条件
(第3课时)用“边角边”判定三角形全等
1.理解并掌握三角形全等判定“边角边”条件的内容并增强学生的探索 能力.(重点)
2.熟练利用“边角边”条件证明两个三角形全等及理解边边角不能判定三 角形全等。(难点)
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
目标学习
到目前为止,你知道哪些判定三角形全等的方法?
边边边(SSS)
复习回顾
S
S
S
S
S
S
角边角(ASA)
A
A
S
S
A
A
角角边(AAS)
A
A
A
A
S
S
角角边(AAS)
A
A
A
A
S
S
特别注意:两全等三角形其对应顶点一般要一一对应:△ABC≌△DEF
根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?
两边一角相等
合作学习
两边及夹角(SAS)
S
A
S
两边和其中一边的对角(SSA)
S
S
A
S
S
A
如果“两边及一角”条件中的角是两边的夹角。若三角形的两条边分别是2.5cm和3.5cm,它们所夹的角为40°,你能画出这个三角形吗
你画的三角形与同伴画的一定全等吗
课本102页做一做
合作学习
步骤:
1、画角∠MAB=40°;
2、在射线AB上截取AC,使它等于2.5cm;
3、在射线AM上截取AD,使它等于3.5cm;
4、连结CD.△ACD即为所求.
合作学习
1.已知条件为“两边及其夹角对应相等”
如图14-21,在△ABC和△A'B'C'中,已知AB=A'B'.∠A= ∠ A',AC=A'C',那么△ABC≌△A'B'C'
说理过程如下:
把△ABC放到△A‘B’C‘上,使 ∠A的顶点与 ∠A’的顶点重合;由于 ∠A= ∠ A‘,因此可以使射线 AB、AC 分别落在射线A’B‘、A’C‘上.因为AB=A’B‘,AC=A’C‘所以点 BC分别与点 BC重合,这样 △ABC 和△A’B‘C’重合,即△ABC≌△A'B'C'.
两边及其夹角分别相等的两个三角形全等
简写成“_______”或“______”)。
边角边
SAS
合作学习
课本103页 议一议
两边分别相等且其中一组等边的对角相等的两个三角形不一定全等,即边边角(SSA)不能判定两个三角形全等。
有两条边和一个角对应相等,这样的两个三角形一定全等吗?
注意:如果用两边和一角相等证明两三角形全等,那么这个角一定要是这两边所夹的角
B
A
C
E
F
D
AB=FE
AC=FD
∠B=∠E
M
两边及其夹角分别相等的两个三角形全等
简写成“_______”或“______”)。
边角边
SAS
总结归纳
课本103页
几何语言
请在课本103页上书写
在△ABC 和△DEF中
AB=DE
S
S
∠B=∠E
A
A
BC=EF
S
S
∴△ABC ≌△DEF
(SAS)
特别注意:两三角形全等其对应顶点一般要一一对应:△ABC≌△DEF
特别注意: 两边分别相等且其中一组等边的对角相等的两个三角形不一定全等,即边边角(SSA)不能判定两个三角形全等。
例题学习
零障碍82页例1
(对顶角相等)
(SAS)
S
S
(已知)
A
A
S
S
(已知)
随堂练习
1.在下列图中找出全等三角形,并把它们用线连起来.
5cm
5cm
)
⑼
)
5cm
5cm
35°
⑴
35°
)
⑺
3cm
4cm
)
⑵
3cm
4cm
⑹
6cm
5cm
⑸
2cm
3cm
⑶
5cm
4cm
⑻
2cm
5cm
⑽
4cm
5cm
⑷
4cm
3cm
随堂练习
2.小明做了一个如图所示的风筝,其中∠ 1=∠2,ED=FD,将上述条件标注在图 中,小明不用测量就能知道EH=FH吗?与同伴 进行交流.
解:是,理由如下:
∵在△EDH和△FDH中
ED=FD(已知)
∠1=∠2(已知)
DH=DH(公共边)
∴△DEH≌△DFH(SAS)
∴EH=FH(全等三角形的对应边相等)
)
)
1
2
随堂练习
3.如图,已知AB=AC,AD=AE
能说明△BOE≌△COD吗?为什么?
解:在△ABD和△ACE中
AB=AC(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴△ABD≌△ACE(SAS)
∴∠B=∠C
(全等三角形对应角相等)
随堂练习
4.如图,两个三角形绕点A旋转,已知AB=AD,AC=AE,∠1=∠2,
试说明:BC=DE.
解:∵∠1= ∠2
∴ ∠1+ ∠ EAC=∠2 +∠EAC
即∠ BAC=∠DAE
在△ABC和△ADE中
AB=AD
∠ BAC=∠DAE
AC=AE
∴△ABC≌△ADE(SAS)
∴BC=DE(全等三角形的对应边相等)
)
)
1
2
随堂练习
5.两个三角形绕点A旋转至如图所示位置若AB=AD,AC=AE,∠BAE=∠DAE,
试说明:BC=DE.
∴△ABC≌△ADE(SAS)
∴BC=DE(全等三角形的对应边相等).
解:∵ ∠BAE=∠DAE
∴ ∠BAE -∠ EAC=∠DAE -∠EAC
即∠ 1=∠2
在△ABC和△ADE中
AB=AD
∠ 1=∠2
AC=AE
随堂练习
6.如图,已知AB=AC,P是△ABC内部任意一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,试说明:BQ=CP.
解:∵ ∠QAP=∠BAC(已知)
∴ ∠QAP-∠BAP=∠BAC-∠BAP
∴∠1=∠2(等式性质)
在△ABQ和△ACP中
AB=AC(已知)
∵ ∠1=∠2(已证)
AQ=QP(已知)
∴ △ABQ≌△ACP(SAS)
∴BQ=CP(全等三角形对应边相等)
1
2
课堂总结
课堂总结
课本P104
习题4.8
同课章节目录
