2024-2025学年八年级下学期数学期考末试(浙江金华市专用)[含答案]
文档属性
| 名称 | 2024-2025学年八年级下学期数学期考末试(浙江金华市专用)[含答案] |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 13:54:12 | ||
图片预览




文档简介
保密★启用前
2024-2025学年八年级下册期末测试卷(金华市专用)
数 学
考试范围:八下全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.请选出各题中一个最符合题意的选项,并在答题卷上将相应题次中对应字母的方框涂黑,不选、多选、错选均不给分.
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.等式成立的条件是( )
A. B. C. D.
3.如图,新疆伊犁特克斯城因八卦布局而被称为“八卦城”,“八卦城”的形状是一个八边形,则八边形的内角和是( )
A. B. C. D.
4.用配方法解方程,变形后结果正确的是( )
A. B. C. D.
5.下列说法正确的是( )
A.矩形的邻边相等
B.菱形的对角线相等
C.平行四边形的对角互补
D.对角线互相垂直的矩形是正方形
6.用反证法证明“若,则”时,应先假设( )
A. B. C. D.
7.在一次主题为“畅想未来”的比赛中,某班5名参赛成员的成绩(单位:分)分别为92,87,94,87,90.关于这组数据,下列说法错误的是( )
A.平均数是89 B.中位数是90 C.众数是87 D.方差是
8. 某建筑工程队在工地一边靠墙处,用81米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为440平方米.为了方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门.若设AB=x米,则可列方程( )
A.x(81﹣4x)=440 B.x(78﹣2x)=440
C.x(84﹣2x)=440 D.x(84﹣4x)=440
9.如图,在平行四边形中,按下列条件得到的四边形不一定是平行四边形的是( )
A.,是过对角线交点的两条线段
B.,,,是四边形各边中点
C.,
D.,,,是角平分线
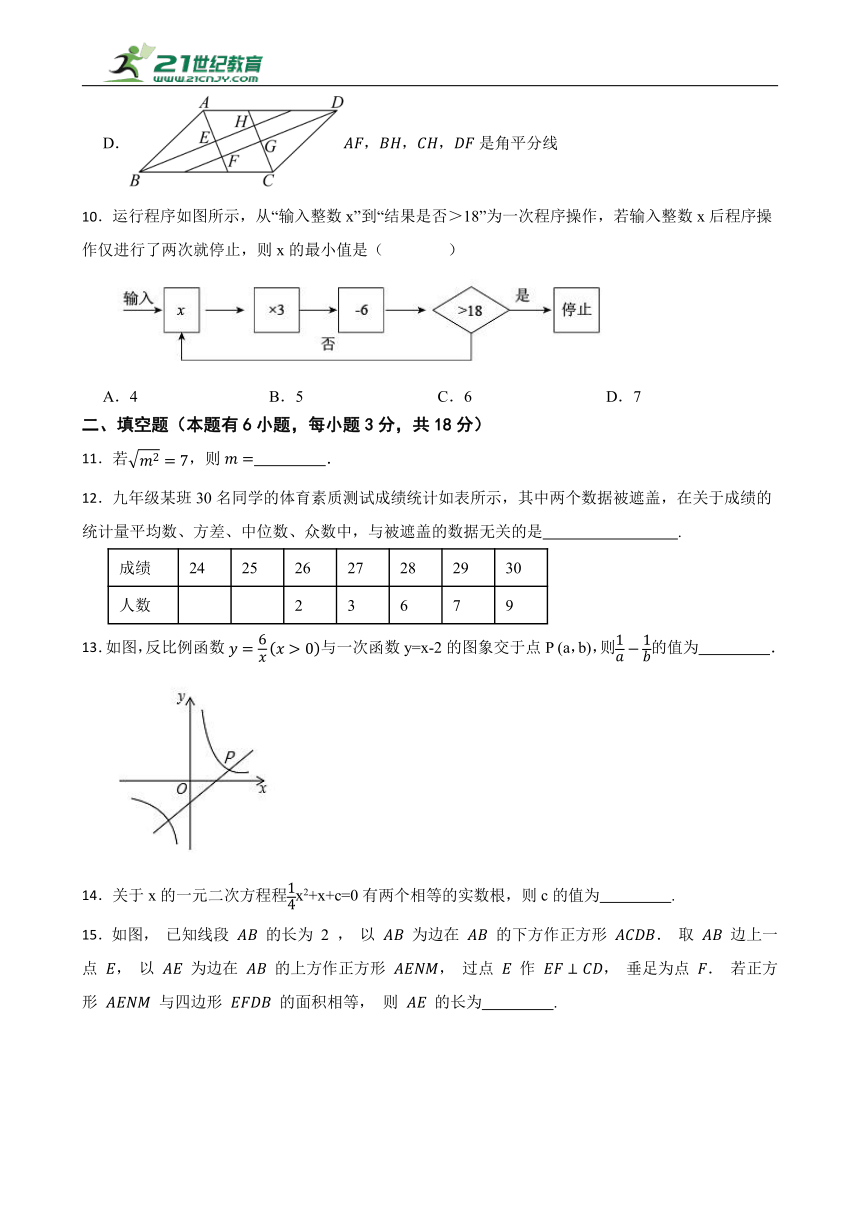
10.运行程序如图所示,从“输入整数x”到“结果是否>18”为一次程序操作,若输入整数x后程序操作仅进行了两次就停止,则x的最小值是( )
A.4 B.5 C.6 D.7
二、填空题(本题有6小题,每小题3分,共18分)
11.若,则 .
12.九年级某班30名同学的体育素质测试成绩统计如表所示,其中两个数据被遮盖,在关于成绩的统计量平均数、方差、中位数、众数中,与被遮盖的数据无关的是 .
成绩 24 25 26 27 28 29 30
人数 2 3 6 7 9
13.如图,反比例函数与一次函数y=x-2的图象交于点P (a,b),则的值为 .
14.关于x的一元二次方程程x2+x+c=0有两个相等的实数根,则c的值为 .
15.如图, 已知线段 的长为 2 , 以 为边在 的下方作正方形 . 取 边上一点 , 以 为边在 的上方作正方形 , 过点 作 , 垂足为点 . 若正方形 与四边形 的面积相等, 则 的长为 .
16.如图,在平行四边形中,,,,,分别是边,上的动点,连结,,为的中点,为的中点,连结,则长的最小值为 .
三、解答题(本题有8小题,共72分)
17.(1)计算:.
(2)计算:.
18.在实数范围内,对于任意实数m、规定一种新运算:,例如:.
(1)计算:;
(2)若的值为4,求的值.
19.如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点均为格点,只用无刻度的直尺,分别在给定的网格中按下列要求作图.
(1)在图①中,以为边作一个菱形(正方形除外),菱形的顶点是格点;
(2)在图②中,以为对角线作一个菱形(正方形除外),菱形的顶点是格点;
(3)在图③中,在上确定一个点,在的内部确定一个非格点,在上确定一个点,连接,使得四边形是平行四边形(保留作图痕迹).
20.如图1,和是的对角线,.点为射线上的一点,连接.
(1)当点在线段的延长线上,且时,
①依题意补全图1;
②求证:;
(2)如图2,当点在线段上,且时,用等式表示线段,和的数量关系,并证明.
21.某校甲乙两班联合举办了“经典阅读”竞赛,从甲班和乙班各随机抽取10名学生.统计这部分学生的竞赛成绩,并对数据(成绩)进行了收集、整理、分析.(成绩得分用x表示,共分成四组:A.;B.;C.;D.)下面给出了部分信息.
【收集数据】
甲班10名学生竞赛成绩:85,78,88,79,72,96,79,69,65,89
乙班10名学生竞赛成绩:85,80,77,85,80,69,99,74,75,81
【整理数据】
【分析数据】
班级 平均数 中位数 众数 方差 C组所占百分比
甲班 80 n 79 84.2
乙班 80 80 a 27
【解决问题】根据以上信息,回答下列问题:
(1)填空: , , ;
(2)请你根据【分析数据】中的信息,判断哪个班成绩比较稳定
(3)按竞赛规定,达到D组成绩可获得一等奖.若甲、乙班两班各有学生50人:请估计这两个班可以获得一等奖的总人数是多少
22.随着电池技术的创新和国家政策的支持,新能源汽车行业正迎来前所未有的发展机遇.某品牌新能源汽车企业从2021年到2023年新能源汽车的销售总量增长了.由于新能源汽车销量的逐年上升,公司仅有的2个工厂无法满足市场需求.公司决定加建工厂,经调研发现,受公司各方资源因素影响,一个工厂的最大产能是6万辆/季度,若每增加1个工厂,每个工厂的最大产能将减少万辆/季度.
(1)求该品牌汽车企业2021年到2023年新能源汽车销售总量的平均年增长率;
(2)现该企业要保证每季度生产汽车27万辆,在增加产能同时又要节省投入成本的条件下,应该再增加几个工厂?
23.如图,在平面直角坐标系中,点 ,把线段绕点逆时针旋转到,交轴于点,反比例函数的图象经过点.
(1)求的值;
(2)连接,若点在反比例函数的图象上,求点的坐标.
24.定义新概念、有一组邻边相等,且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形,,.
①若,于点,求的长;
②若,,求的长;
(2)如图②,在矩形中,,点是对角线上的一点,且,过点作直线分别交边,于点,,要使四边形是等腰直角四边形,求的长.
答案解析部分
1.D
2.C
3.C
4.C
5.D
6.C
解:用反证法证明“若a>b,则-3a<-3b”时,应先假设-3a≥-3b,
故答案:C.
反证法的步骤中,第一步是假设结论不成立,反面成立。
7.A
解:A、这组数据的平均数是(分),所以选项A错误,符合题意;
B、将这组数据从小到大排列为87, 87, 90, 92,94.则中位数是90分,所以选项B正确,不符合题意;
C、组数据的众数是87,选项C正确,不符合题意;
D、这组数据的方差是 90)2+(90-90)2]=7.6(分),所以选项D正确,不符合题意.
故答案为:A.
根据平均数,中位数,众数及方差的计算方法计算即可判断答案.
8.D
解:设仓库的宽为x米 米),则仓库的长为 米,
根据题意得:
故答案为:D.
设仓库的宽为x米( 米),由铁栅栏的长度结合图形,可求出仓库的长为 (84-4x)米,再根据矩形的面积公式即可列出关于x的一元二次方程,此题得解.
9.C
10.B
11.
12.中位数和众数
解:根据表格,成绩为24分和25分的人数和为:30-2-3-6-7-9=3(人)
中位数是成绩从小到大排列后第15和第16人的平均数,故中位数与被遮盖的数据无关.
众数是出现次数最多的数,30分的人数最多,故众数是30,即众数与被遮盖的数据无关.
平均数为所有数据的和÷总人数,方差在平均数基础上进行计算,故都需要知道被遮盖的数据.
故答案为:中位数和众数
根据平均数、方差、中位数、众数的计算公式进行判断即可.
13.
解:,
将P (a,b)分别代入和y=x-2,得
,
,
故答案为:.
根据一次函数和反比例函数图象上的点的坐标特征,将P (a,b)代入反比例函数和一次函数的解析式求得,整体代入代数式计算即可求解.
14.1
解:∵方程 有两个相等的实数根,
则判别式 ,
即
解得,
故答案为:1.
根据方程根的情况得到,然后解方程求出c的值即可.
15.
解:设,
∵四边形和四边形都为正方形,
∴,,四边形为矩形,
∴,
∴,.
∵正方形与四边形的面积相等,
∴,
解得:,(舍),
∴.
故答案为:
设,先根据正方形的性质得到,,四边形为矩形,进而根据矩形的性质得到,从而得到,,再根据面积相等结合题意列出一元二次方程,从而即可求解。
16.
解:如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.
∵四边形ABCD是平行四边形,∠BCD=120°,
∴∠D=180°-∠BCD=60°,AB=CD=2,
∵AM=DM=DC=2,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,CM=DM=AM,
∴∠MAC=∠MCA=30°,
∴∠ACD=90°,
∴AC=2,
在Rt△ACN中,
∵AC=2,∠ACN=∠DAC=30°,
∴AN=AC=,
∵AE=EH,GF=FH,
∴EF=AG,
∵AG≤AC,
∴AG的最大值为AC的长,最小值为AN的长,
∴AG的最大值为2,最小值为,
∴EF的最小值为,
故答案为:.
如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.首先证明∠ACD=90°,求出AC,AN,利用三角形中位线定理,可知EF=AG,求出AG的最最小值即可解决问题。
17.(1),(2).
18.(1)
(2)
19.(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:如图所示,即为所求;
∵,,
∴四边形是平行四边形.
(1)利用勾股定理画出四边形,且满足即可;
(2)利用勾股定理画出四边形,且满足即可;
(3)作出、的平行线即可获得答案.
20.(1)解:① 依题意补全图形
②证明:∵,
∴.
∵ 四边形是平行四边形,
∴
∴.
∵,
∴
∵,
∴.
在和中,
,
∴
∴.
(2)解:线段,和的数量关系为.
证明:延长至点,使得,连接.
由(1)②可得
∴.
∵,
∴.
∵,
∴.
∴.
.
(1)①先根据题意作出图形即可;
②先利用等角对等边及等量代换可得,再利用“SAS”证出,最后利用全等三角形的性质可得;
(2)延长至点,使得,连接,先利用等角对等边及等量代换可得,再利用线段的和差及等量代换可得.
(1)解:① 依题意补全图形
②证明:∵,
∴.
∵ 四边形是平行四边形,
∴
∴.
∵,
∴
∵,
∴.
在和中,
,
∴
∴.
(2)解:线段,和的数量关系为.
证明:延长至点,使得,连接.
由(1)②可得
∴.
∵,
∴.
∵,
∴.
∴.
.
21.(1)40,79,80或85;
(2)乙班的成绩相对稳定
(3)10人
22.(1)
(2)应该再增加3个工厂.
23.(1)解:作轴,垂足为点,
把线段绕点逆时针旋转到,
,,
,
即,
在和中,
,
(),
,,
点,
,,
点的坐标为,,
反比例函数的图象经过点,
;
(2)解:设的解析式为,
点,
,
解得,
的解析式为,
令,则,
点的坐标为,
,
,
,
设点坐标为,
,
,
解得,
点坐标为.
(1)作轴,垂足为点,根据旋转的性质得到,,进而得到即可利用"AAS"证明,得到即可得到点C的坐标,继而求出k的值;
(2)设的解析式为,利用待定系数法即可求出AC的解析式,然后令x=0,得到点D的坐标,然后利用勾股定理即可求出AB的长度,的面积,设点坐标为,根据题意列方程即可求解.
24.(1)解:①连接,如图所示:
∵,,
∴,
∵,
∴,
∴;
②连接、,交于点,过点C作,交于点E,如图所示:
则,
∵,,
∴,
∴,
∵,,
∴、在线段的垂直平分线上,
∴垂直平分,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,,
∴.
(2)解:∵四边形为矩形,∴,,,;
若时,如图所示:
则四边形和为矩形,
∴,,,
∵,
∴,
∴,
∵,
∴,,
∴,
∴,;
∴四边形不可能是等腰直角四边形;
若与不垂直,当时,如图所示:
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴此时点F不在边上,不符合题意;
若与不垂直,当时,如图所示:
此时四边形是等腰直角四边形,
∴,
∵,
∴,
∴,
∴,
∴,
综上所述,满足条件的的长为.
(1)①根据勾股定理求出,再根据勾股定理求出的值;
②连接、,交于点,过点C作,交于点E,证明垂直平分,得出,证明,得出,证明,得出,根据勾股定理求出,即可得出答案;
(2)若,则,,推出四边形不是等腰直角四边形,不符合条件.若与不垂直,当时,此时四边形是等腰直角四边形,当时,此时四边形是等腰直角四边形,分别求解即可.
(1)解:①连接,如图所示:
∵,,
∴,
∵,
∴,
∴;
②连接、,交于点,过点C作,交于点E,如图所示:
则,
∵,,
∴,
∴,
∵,,
∴、在线段的垂直平分线上,
∴垂直平分,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,,
∴.
(2)解:∵四边形为矩形,
∴,,,;
若时,如图所示:
则四边形和为矩形,
∴,,,
∵,
∴,
∴,
∵,
∴,,
∴,
∴,;
∴四边形不可能是等腰直角四边形;
若与不垂直,当时,如图所示:
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴此时点F不在边上,不符合题意;
若与不垂直,当时,如图所示:
此时四边形是等腰直角四边形,
∴,
∵,
∴,
∴,
∴,
∴,
综上所述,满足条件的的长为.
2024-2025学年八年级下册期末测试卷(金华市专用)
数 学
考试范围:八下全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.请选出各题中一个最符合题意的选项,并在答题卷上将相应题次中对应字母的方框涂黑,不选、多选、错选均不给分.
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.等式成立的条件是( )
A. B. C. D.
3.如图,新疆伊犁特克斯城因八卦布局而被称为“八卦城”,“八卦城”的形状是一个八边形,则八边形的内角和是( )
A. B. C. D.
4.用配方法解方程,变形后结果正确的是( )
A. B. C. D.
5.下列说法正确的是( )
A.矩形的邻边相等
B.菱形的对角线相等
C.平行四边形的对角互补
D.对角线互相垂直的矩形是正方形
6.用反证法证明“若,则”时,应先假设( )
A. B. C. D.
7.在一次主题为“畅想未来”的比赛中,某班5名参赛成员的成绩(单位:分)分别为92,87,94,87,90.关于这组数据,下列说法错误的是( )
A.平均数是89 B.中位数是90 C.众数是87 D.方差是
8. 某建筑工程队在工地一边靠墙处,用81米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为440平方米.为了方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门.若设AB=x米,则可列方程( )
A.x(81﹣4x)=440 B.x(78﹣2x)=440
C.x(84﹣2x)=440 D.x(84﹣4x)=440
9.如图,在平行四边形中,按下列条件得到的四边形不一定是平行四边形的是( )
A.,是过对角线交点的两条线段
B.,,,是四边形各边中点
C.,
D.,,,是角平分线
10.运行程序如图所示,从“输入整数x”到“结果是否>18”为一次程序操作,若输入整数x后程序操作仅进行了两次就停止,则x的最小值是( )
A.4 B.5 C.6 D.7
二、填空题(本题有6小题,每小题3分,共18分)
11.若,则 .
12.九年级某班30名同学的体育素质测试成绩统计如表所示,其中两个数据被遮盖,在关于成绩的统计量平均数、方差、中位数、众数中,与被遮盖的数据无关的是 .
成绩 24 25 26 27 28 29 30
人数 2 3 6 7 9
13.如图,反比例函数与一次函数y=x-2的图象交于点P (a,b),则的值为 .
14.关于x的一元二次方程程x2+x+c=0有两个相等的实数根,则c的值为 .
15.如图, 已知线段 的长为 2 , 以 为边在 的下方作正方形 . 取 边上一点 , 以 为边在 的上方作正方形 , 过点 作 , 垂足为点 . 若正方形 与四边形 的面积相等, 则 的长为 .
16.如图,在平行四边形中,,,,,分别是边,上的动点,连结,,为的中点,为的中点,连结,则长的最小值为 .
三、解答题(本题有8小题,共72分)
17.(1)计算:.
(2)计算:.
18.在实数范围内,对于任意实数m、规定一种新运算:,例如:.
(1)计算:;
(2)若的值为4,求的值.
19.如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点均为格点,只用无刻度的直尺,分别在给定的网格中按下列要求作图.
(1)在图①中,以为边作一个菱形(正方形除外),菱形的顶点是格点;
(2)在图②中,以为对角线作一个菱形(正方形除外),菱形的顶点是格点;
(3)在图③中,在上确定一个点,在的内部确定一个非格点,在上确定一个点,连接,使得四边形是平行四边形(保留作图痕迹).
20.如图1,和是的对角线,.点为射线上的一点,连接.
(1)当点在线段的延长线上,且时,
①依题意补全图1;
②求证:;
(2)如图2,当点在线段上,且时,用等式表示线段,和的数量关系,并证明.
21.某校甲乙两班联合举办了“经典阅读”竞赛,从甲班和乙班各随机抽取10名学生.统计这部分学生的竞赛成绩,并对数据(成绩)进行了收集、整理、分析.(成绩得分用x表示,共分成四组:A.;B.;C.;D.)下面给出了部分信息.
【收集数据】
甲班10名学生竞赛成绩:85,78,88,79,72,96,79,69,65,89
乙班10名学生竞赛成绩:85,80,77,85,80,69,99,74,75,81
【整理数据】
【分析数据】
班级 平均数 中位数 众数 方差 C组所占百分比
甲班 80 n 79 84.2
乙班 80 80 a 27
【解决问题】根据以上信息,回答下列问题:
(1)填空: , , ;
(2)请你根据【分析数据】中的信息,判断哪个班成绩比较稳定
(3)按竞赛规定,达到D组成绩可获得一等奖.若甲、乙班两班各有学生50人:请估计这两个班可以获得一等奖的总人数是多少
22.随着电池技术的创新和国家政策的支持,新能源汽车行业正迎来前所未有的发展机遇.某品牌新能源汽车企业从2021年到2023年新能源汽车的销售总量增长了.由于新能源汽车销量的逐年上升,公司仅有的2个工厂无法满足市场需求.公司决定加建工厂,经调研发现,受公司各方资源因素影响,一个工厂的最大产能是6万辆/季度,若每增加1个工厂,每个工厂的最大产能将减少万辆/季度.
(1)求该品牌汽车企业2021年到2023年新能源汽车销售总量的平均年增长率;
(2)现该企业要保证每季度生产汽车27万辆,在增加产能同时又要节省投入成本的条件下,应该再增加几个工厂?
23.如图,在平面直角坐标系中,点 ,把线段绕点逆时针旋转到,交轴于点,反比例函数的图象经过点.
(1)求的值;
(2)连接,若点在反比例函数的图象上,求点的坐标.
24.定义新概念、有一组邻边相等,且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形,,.
①若,于点,求的长;
②若,,求的长;
(2)如图②,在矩形中,,点是对角线上的一点,且,过点作直线分别交边,于点,,要使四边形是等腰直角四边形,求的长.
答案解析部分
1.D
2.C
3.C
4.C
5.D
6.C
解:用反证法证明“若a>b,则-3a<-3b”时,应先假设-3a≥-3b,
故答案:C.
反证法的步骤中,第一步是假设结论不成立,反面成立。
7.A
解:A、这组数据的平均数是(分),所以选项A错误,符合题意;
B、将这组数据从小到大排列为87, 87, 90, 92,94.则中位数是90分,所以选项B正确,不符合题意;
C、组数据的众数是87,选项C正确,不符合题意;
D、这组数据的方差是 90)2+(90-90)2]=7.6(分),所以选项D正确,不符合题意.
故答案为:A.
根据平均数,中位数,众数及方差的计算方法计算即可判断答案.
8.D
解:设仓库的宽为x米 米),则仓库的长为 米,
根据题意得:
故答案为:D.
设仓库的宽为x米( 米),由铁栅栏的长度结合图形,可求出仓库的长为 (84-4x)米,再根据矩形的面积公式即可列出关于x的一元二次方程,此题得解.
9.C
10.B
11.
12.中位数和众数
解:根据表格,成绩为24分和25分的人数和为:30-2-3-6-7-9=3(人)
中位数是成绩从小到大排列后第15和第16人的平均数,故中位数与被遮盖的数据无关.
众数是出现次数最多的数,30分的人数最多,故众数是30,即众数与被遮盖的数据无关.
平均数为所有数据的和÷总人数,方差在平均数基础上进行计算,故都需要知道被遮盖的数据.
故答案为:中位数和众数
根据平均数、方差、中位数、众数的计算公式进行判断即可.
13.
解:,
将P (a,b)分别代入和y=x-2,得
,
,
故答案为:.
根据一次函数和反比例函数图象上的点的坐标特征,将P (a,b)代入反比例函数和一次函数的解析式求得,整体代入代数式计算即可求解.
14.1
解:∵方程 有两个相等的实数根,
则判别式 ,
即
解得,
故答案为:1.
根据方程根的情况得到,然后解方程求出c的值即可.
15.
解:设,
∵四边形和四边形都为正方形,
∴,,四边形为矩形,
∴,
∴,.
∵正方形与四边形的面积相等,
∴,
解得:,(舍),
∴.
故答案为:
设,先根据正方形的性质得到,,四边形为矩形,进而根据矩形的性质得到,从而得到,,再根据面积相等结合题意列出一元二次方程,从而即可求解。
16.
解:如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.
∵四边形ABCD是平行四边形,∠BCD=120°,
∴∠D=180°-∠BCD=60°,AB=CD=2,
∵AM=DM=DC=2,
∴△CDM是等边三角形,
∴∠DMC=∠MCD=60°,CM=DM=AM,
∴∠MAC=∠MCA=30°,
∴∠ACD=90°,
∴AC=2,
在Rt△ACN中,
∵AC=2,∠ACN=∠DAC=30°,
∴AN=AC=,
∵AE=EH,GF=FH,
∴EF=AG,
∵AG≤AC,
∴AG的最大值为AC的长,最小值为AN的长,
∴AG的最大值为2,最小值为,
∴EF的最小值为,
故答案为:.
如图,取AD的中点M,连接CM、AG、AC,作AN⊥BC于N.首先证明∠ACD=90°,求出AC,AN,利用三角形中位线定理,可知EF=AG,求出AG的最最小值即可解决问题。
17.(1),(2).
18.(1)
(2)
19.(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:如图所示,即为所求;
∵,,
∴四边形是平行四边形.
(1)利用勾股定理画出四边形,且满足即可;
(2)利用勾股定理画出四边形,且满足即可;
(3)作出、的平行线即可获得答案.
20.(1)解:① 依题意补全图形
②证明:∵,
∴.
∵ 四边形是平行四边形,
∴
∴.
∵,
∴
∵,
∴.
在和中,
,
∴
∴.
(2)解:线段,和的数量关系为.
证明:延长至点,使得,连接.
由(1)②可得
∴.
∵,
∴.
∵,
∴.
∴.
.
(1)①先根据题意作出图形即可;
②先利用等角对等边及等量代换可得,再利用“SAS”证出,最后利用全等三角形的性质可得;
(2)延长至点,使得,连接,先利用等角对等边及等量代换可得,再利用线段的和差及等量代换可得.
(1)解:① 依题意补全图形
②证明:∵,
∴.
∵ 四边形是平行四边形,
∴
∴.
∵,
∴
∵,
∴.
在和中,
,
∴
∴.
(2)解:线段,和的数量关系为.
证明:延长至点,使得,连接.
由(1)②可得
∴.
∵,
∴.
∵,
∴.
∴.
.
21.(1)40,79,80或85;
(2)乙班的成绩相对稳定
(3)10人
22.(1)
(2)应该再增加3个工厂.
23.(1)解:作轴,垂足为点,
把线段绕点逆时针旋转到,
,,
,
即,
在和中,
,
(),
,,
点,
,,
点的坐标为,,
反比例函数的图象经过点,
;
(2)解:设的解析式为,
点,
,
解得,
的解析式为,
令,则,
点的坐标为,
,
,
,
设点坐标为,
,
,
解得,
点坐标为.
(1)作轴,垂足为点,根据旋转的性质得到,,进而得到即可利用"AAS"证明,得到即可得到点C的坐标,继而求出k的值;
(2)设的解析式为,利用待定系数法即可求出AC的解析式,然后令x=0,得到点D的坐标,然后利用勾股定理即可求出AB的长度,的面积,设点坐标为,根据题意列方程即可求解.
24.(1)解:①连接,如图所示:
∵,,
∴,
∵,
∴,
∴;
②连接、,交于点,过点C作,交于点E,如图所示:
则,
∵,,
∴,
∴,
∵,,
∴、在线段的垂直平分线上,
∴垂直平分,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,,
∴.
(2)解:∵四边形为矩形,∴,,,;
若时,如图所示:
则四边形和为矩形,
∴,,,
∵,
∴,
∴,
∵,
∴,,
∴,
∴,;
∴四边形不可能是等腰直角四边形;
若与不垂直,当时,如图所示:
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴此时点F不在边上,不符合题意;
若与不垂直,当时,如图所示:
此时四边形是等腰直角四边形,
∴,
∵,
∴,
∴,
∴,
∴,
综上所述,满足条件的的长为.
(1)①根据勾股定理求出,再根据勾股定理求出的值;
②连接、,交于点,过点C作,交于点E,证明垂直平分,得出,证明,得出,证明,得出,根据勾股定理求出,即可得出答案;
(2)若,则,,推出四边形不是等腰直角四边形,不符合条件.若与不垂直,当时,此时四边形是等腰直角四边形,当时,此时四边形是等腰直角四边形,分别求解即可.
(1)解:①连接,如图所示:
∵,,
∴,
∵,
∴,
∴;
②连接、,交于点,过点C作,交于点E,如图所示:
则,
∵,,
∴,
∴,
∵,,
∴、在线段的垂直平分线上,
∴垂直平分,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,,
∴.
(2)解:∵四边形为矩形,
∴,,,;
若时,如图所示:
则四边形和为矩形,
∴,,,
∵,
∴,
∴,
∵,
∴,,
∴,
∴,;
∴四边形不可能是等腰直角四边形;
若与不垂直,当时,如图所示:
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴此时点F不在边上,不符合题意;
若与不垂直,当时,如图所示:
此时四边形是等腰直角四边形,
∴,
∵,
∴,
∴,
∴,
∴,
综上所述,满足条件的的长为.
同课章节目录
