2024-2025学年八年级下学期数学期考末试(浙江绍兴市专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年八年级下学期数学期考末试(浙江绍兴市专用)[答案+解析] |  | |
| 格式 | docx | ||
| 文件大小 | 449.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 14:04:53 | ||
图片预览



文档简介
保密★启用前
2024-2025学年八年级下册期末测试卷(绍兴市专用)
数 学
考试范围:八下全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列实数中,无理数是( )
A. B.0 C. D.
2.若关于 的一元二次方程 有一个根为 0 , 则 的值等于( )
A.-1 B.0 C.1 D.1 或者 -1
3.已知是反比例函数的图像上的三点,且,则下列命题是真命题的是( )
A.若且,则
B.若且,则0
C.若且,则
D.若且,则0
4.直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
5.小明在处理一组数据“12,12,28,35,■”时,不小心将其中一个数据污染了,只记得该数据在30~40之间,则“■”在范围内无论为何值都不影响这组数据的( )
A.平均数 B.众数 C.中位数 D.方差
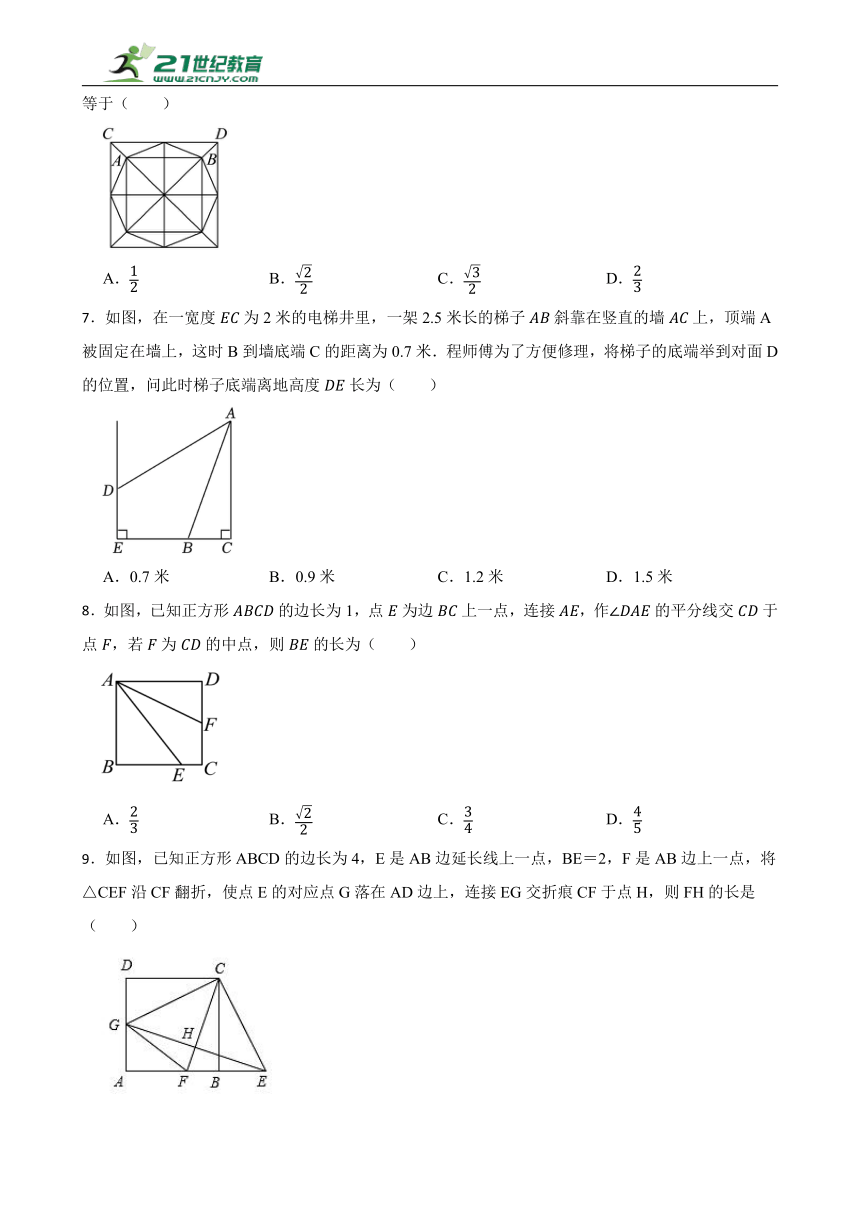
6.孝泉古镇是川西平原的一颗明珠,具有丰富的孝文化内涵和历史底蕴,孝泉古名阳泉县,仁寿二年(602)废县,唐置姜诗镇,北宋英宗治平年间因避姜诗名讳,本其事迹,更名为孝泉镇.古镇上诸多亭廊的设计兼具实用性和审美性.如图,某亭子的平面图是由正方形和正八边形复合而成,则等于( )
A. B. C. D.
7.如图,在一宽度为2米的电梯井里,一架2.5米长的梯子斜靠在竖直的墙上,顶端A被固定在墙上,这时B到墙底端C的距离为0.7米.程师傅为了方便修理,将梯子的底端举到对面D的位置,问此时梯子底端离地高度长为( )
A.0.7米 B.0.9米 C.1.2米 D.1.5米
8.如图,已知正方形的边长为1,点为边上一点,连接,作的平分线交于点,若为的中点,则的长为( )
A. B. C. D.
9.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是( )
A. B. C.1 D.
10.下列说法:
若一元二次方程 有一个根是 ,则代数式 的值是 若 ,则 是一元二次方程 的一个根 若 ,则一元二次方程 有不相等的两个实数根 当m取整数 或1时,关于x的一元二次方程 与 的解都是整数.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题有8小题,每小题3分,共24分.请将本题答案用签字笔或钢笔写在答题卡对应答题区域内.)
11.若二次根式在实数范围内有意义,则x的取值范围是 .
12.已知关于 的方程 有两个相等的实数根,则 的值是 ..
13.数据 的方差计算公式为 则这组数据的和是 .
14. 如图,在中,以点为圆心长为半径作弧交于点,分别以点、为圆心,同样长度为半径作弧,交于点,连接并延长交于点,若,,则的长为 .
15.《九章算术》中提出了如下问题: 今有户不知高、广, 竿不知长短. 横之不出四尺, 从之不出二尺, 邪之适出. 问户高、广、邪各几何? 这段话的意思是: 今有门不知其高宽; 有竿, 不知其长短, 横放, 竿比门宽长出 4 尺;坚放,竿比门高长出 2 尺; 斜放,笔与门对角线恰好相等. 问门高、宽和对角线的长各是多少. 则该问题中的门高是 尺.
16. 如图,在中,,,点E是上一点,将四边形沿翻折得到四边形,点D正好落在延长线上的点F处.
(1)的长为 ;
(2)连接,若,则的度数是 .
17.如图,菱形ABCD的边长为3,∠BAD=60°,点E,F在对角线AC上(点E在点F 的左侧),且EF=1,则DE+BF的最小值为 .
18.如图,反比例函数的图象与矩形的边、分别交于点、,已知点的纵坐标为,点的横坐标为,则的值为 .
三、解答题(本大题有6小题,共46分.解答需写出必要的文字说明、演算步骤或证明过程.)
19.计算:
(1)
(2).
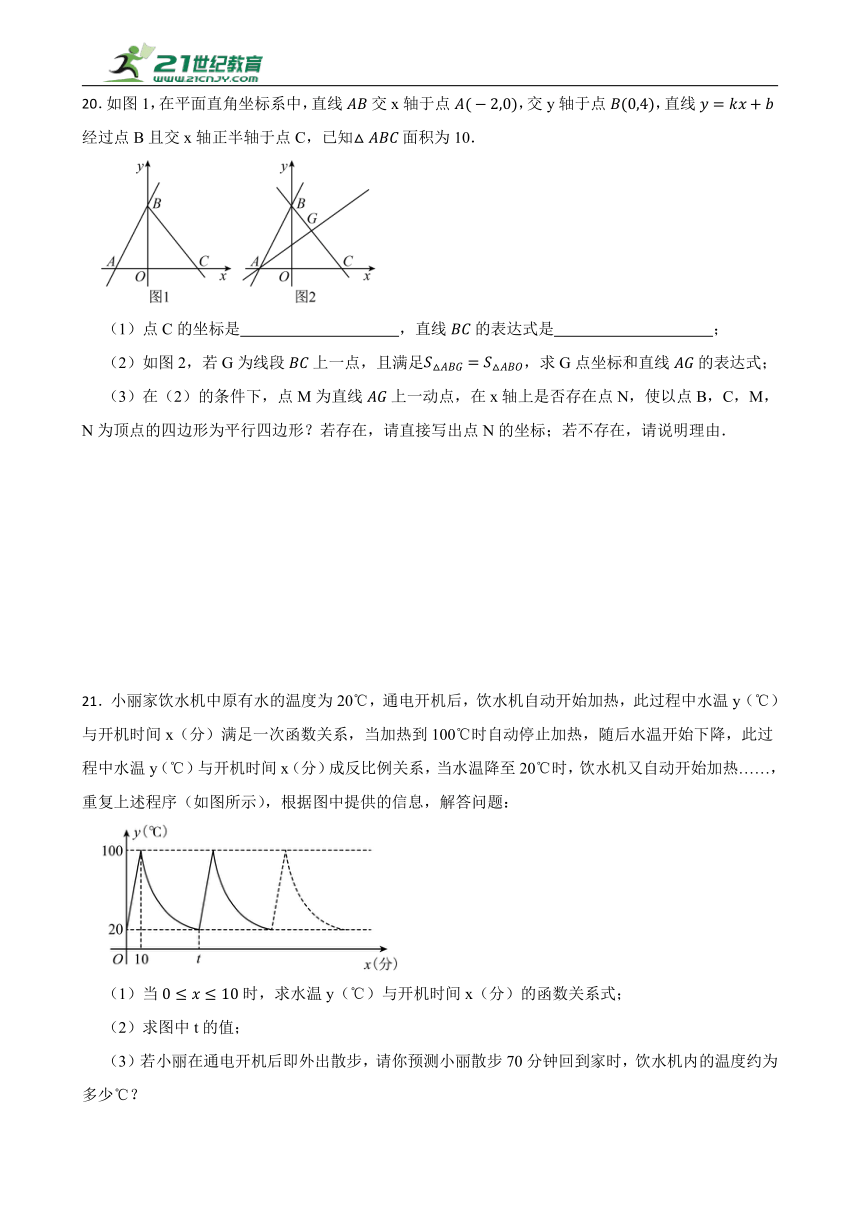
20.如图1,在平面直角坐标系中,直线交x轴于点,交y轴于点,直线经过点B且交x轴正半轴于点C,已知面积为10.
(1)点C的坐标是 ,直线的表达式是 ;
(2)如图2,若G为线段上一点,且满足,求G点坐标和直线的表达式;
(3)在(2)的条件下,点M为直线上一动点,在x轴上是否存在点N,使以点B,C,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
21.小丽家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题:
(1)当时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小丽在通电开机后即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的温度约为多少℃?
22.为弘扬向善、为善优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在”的捐款活动,七年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是 ,并补全条形统计图;
(2)请求出本次捐款金额的众数和中位数;
(3)若这所学校七年级学生为1300名,捐款总金额约有多少元?
23.如图,一次函数分别交y轴,x轴于点,将线段向上平移a个单位长度,再向右平移b个单位长度,得到线段,点A的对应点为点C,点B的对应点为点D,反比例函数经过点.
(1)求的数量关系;
(2)若,直接写出反比例函数表达式.
24.如图①,将△ABC绕点A逆时针旋转90°得到△ADE.
(1)DE与BC的位置关系为 ;
(2)如图②,连接CD,BE,若M为BE的中点,连接AM,请探究线段AM与CD的关系,并给予证明;
(3)如图③,已知E是正方形ABCD的边BC上任意一点,以AE为边作正方形AEFG,连接BG,M为BG的中点,连接AM.
①若AB=4,BE=3,求AM的长;
②若AB=a,BE=b,则AM的长为 .(用含a,b的代数式表示)
答案解析部分
1.D
2.A
一元二次方程 有一个根为 0 ,
∴a-1≠0且
∴a≠1且a=±1
∴a=-1
故答案为A.
首先是一元二次方程,所以a-1≠0,再把x=0代入得,解出a的值即可.
3.D
解:A、,
∵,且,
∴,
∴,但无法确定的正负,
∴无法确定的正负,故A不符合题意;
B、,
∵,且,
∴,但无法确定的正负,
∴无法确定的正负,
∴无法确定的正负,故B不符合题意;
C、,
∵,且,
∴,但无法确定的正负,
∴无法确定的正负,
∴无法确定的正负,故C不符合题意;
D、,
∵,且,
∴,
∴,
∴0 ,故D正确;
故答案为:D.
求出,结合条件得,于是得,但无法确定的正负,即可判断A不符合题意;求出,结合条件得,但无法确定的正负,即可判断B不符合题意;求出,结合条件得,但无法确定的正负,即可判断C不符合题意;求出,结合条件得,,即可判断D符合题意.
4.B
解:解:由题意得正六边形每个内角为,六边形MBCDEN的内角和为,
∴,
∴,
∵,
∴,
故答案为:B
先根据正多边形的内角和内角和得到正六边形每个内角为,六边形的内角和为,进而即可得到,从而得到,再根据“”代入化简即可求解。
5.C
6.B
7.B
8.C
9.B
解:∵四边形是边长为的正方形,
∴,,
∴,
由翻折得,,垂直平分,
在和中,
,
∴,
∴,
∴,
∵,
∴,
∵,且,
∴,
解得,
∵,
∴,
解得,
故选:.
由翻折的性质可得,,垂直平分,然后利用“”证明,即可得到,求得,再利用勾股定理求出,再由,求出,再利用三角形的面积求出FH长解题即可.
10.B
解:①若一元二次方程x2+bx+a=0有一个根是-a(a≠0),则a2+b×(-a)+a=0
整理得出:a(a-b+1)=0,则代数式a-b=-1,正确;
②若a+b+c=0,则x=1是一元二次方程ax2+bx+c=0的一个根,不正确;
③若b=2a+3c,那么△=b2-4ac=(2a+3c)2-4ac=(2a+2c)2+5c2,
当a≠0,c=-a时,△>0;当a≠0,c=0时,△>0;当a≠c≠0时,△>0,
∴△>0,正确;
④∵关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0有解,
则m≠0,
∴△≥0
mx2-4x+4=0,
∴△=16-16m≥0,即m≤1;
x2-4mx+4m2-4m-5=0,
△=16m2-16m2+16m+20≥0,
∴4m+5≥0,m≥- ;
∴- ≤m≤1,而m是整数,
所以m=1,m=0(舍去),m=-1(一个为x2-4x+4=0,另一个为x2+4x+3=0,冲突,故舍去),
当m=1时,mx2-4x+4=0即x2-4x+4=0,方程的解是x1=x2=2;
x2-4mx+4m2-4m-5=0即x2-4x-5=0,方程的解是x1=5,x2=-1;
当m=0时,mx2-4x+4=0时,方程是-4x+4=0不是一元二次方程,故舍去.
故m=1,故不符合题意;
故正确的有2个,
故答案为:B.
①根据方程根的定义将x= a代入方程得出a b的值即可;
②利用a+b+c=0,即x=1是一元二次方程ax2+bx+c=0的一个根得出答案,③利用b=2a+3c,算出方程根的判别式的值,分析判别式的值得出即可;
④根据关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0有解,得出根与判别式△≥0,且m≠0,从而列出关于m不等式,求解求得m的范围,再根据m是整数,即可得到m的可能取到的几个值,然后对每个值进行检验,是否符合使两个一元二次方程的解都是整数即可确定m的值,综上所述即可得出答案.
11.
由得故填
考查二次根式有意义条件,由被开方数是非负数得不等式,会解不等式求解,易错点非负数的表示。
12.1
解:∵关于x的一元二次方程 有两个相等的实数根,∴△=0,∴4﹣4m=0,∴m=1。
故答案为:1。
根据一元二次方程根的判别式,由关于x的一元二次方程 有两个相等的实数根得出其根的判别式的值等于0,从而列出方程,求解即可。
13.
14.
解:如图,
连接EF,设AE交BF于点O,
由作图可知:AB=AF,AE平分∠BAD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB=∠EAB,
∴AB=BE,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴AE⊥BF,
∴AO=OE=AE,BO=OF=3,
在Rt△AOB中,AO=,
∴AE=2AO=2.
故答案为:2.
连接EF,设AE交BF于点O,根据一组对边平行且相等的四边形是平行四边形可得四边形ABEF是平行四边形,再根据一组邻边相等的平行四边形是菱形可得四边形ABEF是菱形,在Rt△AOB中,用勾股定理求出AO的值,然后根据菱形的性质得AE=2AO可求解.
15.8
16.(1)2
(2)60
解:(1)根据翻折性质可得,
四边形ABCD是平行四边形,
AB=AE=4,
CE=BC-BE=2,
(2)取AE的中点M,连接DM,DE,如图,
由翻折可知,AD=AF,
M是AE的中点,
DM=EM=AM==DE,
是等边三角形,
故答案为:60.
(1)利用翻折的性质得到再利用平行四边形的性质求得进而得到于是由AB=AE=4,从而求解;
(2)取AE的中点M,连接DM,DE,利用翻折的性质得到AD=AF,利用勾股定理求得DE,AE的值,再证明是等边三角形,进而求解.
17.
解:如图, 作DM∥AC, 使得DM=EF =1, 连接BM交AC于F,
∵DM =EF,DM∥EF,
∴四边形DEFM是平行四边形,
∴DE=FM,
∴DE+BF =FM+FB= BM,根据两点之间线段最短可知,此时DE+FB最短,
∵四边形ABCD是菱形, AB=3, ∠BAD=60°
∴AD=AB,
∴△ABD是等边三角形,
∴BD=AB=3,
在Rt△BDM中,
∴DE+BF的最小值为
故答案为
作DM∥AC, 使得DM = EF= 1, 连接BM交AC于F,由四边形DEFM是平行四边形,推出DE=FM, 推出DE+BF=FM+FB=BM, 根据两点之间线段最短可知,此时DE+FB最短, 由四边形ABCD是菱形, 在Rt△BDM中, 根据 计算即可.
18.
解:连接、,
∵矩形OACB与反比例函数 的图象相交于点E、D,
,
,
又∵ 点的纵坐标为,点的横坐标为,
∴OA=m,OB=,
,
.
故答案为:.
根据反比例函数k的几何意义可得,结合三角形面积计算公式可得,从而代入OA、OB的值,化简整理可得结论.
19.(1)
(2)
20.(1)
(2)解:连接,
∵,
∴,
设的解析式为,
将点,代入,得
,
解得,
∴,
∴的解析式为,
∴,
∴,
∴,
设的解析式为,
将点A、G代入可得
,
解得,
∴;
(3)存在,N点坐标为或或
解:(1)∵面积为10,
∴,
∴,
∵,
∴,
将点B与C的坐标代入,可得
,
∴,
∴,
故答案为,;
(3)∵点M为直线上动点,点N在x轴上,
则可设,,
①当分别为对角线时,
的中点为,的中点为,
∴,,
∴,,
∴;
②当分别为对角线时,
的中点为,的中点为,
∴,,
∴,,
∴;
③当分别为对角线时,
的中点为,的中点为,
∴,,
∴,,
∴;
综上所述:以点B,C,M,N为顶点的四边形为平行四边形时,N点坐标为或或.
(1)根据三角形面积可得AC,再根据两点间距离可得点C坐标,根据待定系数法将点B,C坐标代入解析式即可求出答案.
(2)根据三角形面积可得,设的解析式为,根据待定系数法将点A,B坐标代入解析式可得,根据直线平行性质可得的解析式为,联立两直线方程可得,设的解析式为,根据待定系数法将点A,G坐标代入解析式即可求出答案.
(3)设,,分情况讨论:①当分别为对角线时,②当分别为对角线时,③当分别为对角线时,根据线段中点建立方程,解方程即可求出答案.
21.(1)解:当时,设.
将点,代入上式,
得,解得.
(2)解:当时,设,
将点代入上式,
得,解得,
,
将点代入,
得,解得.
(3)解:由题可知,开机分钟与开机分钟时饮水机的水温相等,
当时,.
小丽散步分钟回到家时,饮水机内的温度约为.
(1)利用待定系数法求一次函数解析式,即可;
(2)利用待定系数法求反比例函数解析式,再将代入解析式,即可得的值;
(3)利用已知由x=20代入求出饮水机内的水的温度即可.
22.(1)50
(2)15,15
(3)17420元
23.(1)
(2)
24.(1);
(2),,
(3)①;②.
2024-2025学年八年级下册期末测试卷(绍兴市专用)
数 学
考试范围:八下全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列实数中,无理数是( )
A. B.0 C. D.
2.若关于 的一元二次方程 有一个根为 0 , 则 的值等于( )
A.-1 B.0 C.1 D.1 或者 -1
3.已知是反比例函数的图像上的三点,且,则下列命题是真命题的是( )
A.若且,则
B.若且,则0
C.若且,则
D.若且,则0
4.直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
5.小明在处理一组数据“12,12,28,35,■”时,不小心将其中一个数据污染了,只记得该数据在30~40之间,则“■”在范围内无论为何值都不影响这组数据的( )
A.平均数 B.众数 C.中位数 D.方差
6.孝泉古镇是川西平原的一颗明珠,具有丰富的孝文化内涵和历史底蕴,孝泉古名阳泉县,仁寿二年(602)废县,唐置姜诗镇,北宋英宗治平年间因避姜诗名讳,本其事迹,更名为孝泉镇.古镇上诸多亭廊的设计兼具实用性和审美性.如图,某亭子的平面图是由正方形和正八边形复合而成,则等于( )
A. B. C. D.
7.如图,在一宽度为2米的电梯井里,一架2.5米长的梯子斜靠在竖直的墙上,顶端A被固定在墙上,这时B到墙底端C的距离为0.7米.程师傅为了方便修理,将梯子的底端举到对面D的位置,问此时梯子底端离地高度长为( )
A.0.7米 B.0.9米 C.1.2米 D.1.5米
8.如图,已知正方形的边长为1,点为边上一点,连接,作的平分线交于点,若为的中点,则的长为( )
A. B. C. D.
9.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是( )
A. B. C.1 D.
10.下列说法:
若一元二次方程 有一个根是 ,则代数式 的值是 若 ,则 是一元二次方程 的一个根 若 ,则一元二次方程 有不相等的两个实数根 当m取整数 或1时,关于x的一元二次方程 与 的解都是整数.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题有8小题,每小题3分,共24分.请将本题答案用签字笔或钢笔写在答题卡对应答题区域内.)
11.若二次根式在实数范围内有意义,则x的取值范围是 .
12.已知关于 的方程 有两个相等的实数根,则 的值是 ..
13.数据 的方差计算公式为 则这组数据的和是 .
14. 如图,在中,以点为圆心长为半径作弧交于点,分别以点、为圆心,同样长度为半径作弧,交于点,连接并延长交于点,若,,则的长为 .
15.《九章算术》中提出了如下问题: 今有户不知高、广, 竿不知长短. 横之不出四尺, 从之不出二尺, 邪之适出. 问户高、广、邪各几何? 这段话的意思是: 今有门不知其高宽; 有竿, 不知其长短, 横放, 竿比门宽长出 4 尺;坚放,竿比门高长出 2 尺; 斜放,笔与门对角线恰好相等. 问门高、宽和对角线的长各是多少. 则该问题中的门高是 尺.
16. 如图,在中,,,点E是上一点,将四边形沿翻折得到四边形,点D正好落在延长线上的点F处.
(1)的长为 ;
(2)连接,若,则的度数是 .
17.如图,菱形ABCD的边长为3,∠BAD=60°,点E,F在对角线AC上(点E在点F 的左侧),且EF=1,则DE+BF的最小值为 .
18.如图,反比例函数的图象与矩形的边、分别交于点、,已知点的纵坐标为,点的横坐标为,则的值为 .
三、解答题(本大题有6小题,共46分.解答需写出必要的文字说明、演算步骤或证明过程.)
19.计算:
(1)
(2).
20.如图1,在平面直角坐标系中,直线交x轴于点,交y轴于点,直线经过点B且交x轴正半轴于点C,已知面积为10.
(1)点C的坐标是 ,直线的表达式是 ;
(2)如图2,若G为线段上一点,且满足,求G点坐标和直线的表达式;
(3)在(2)的条件下,点M为直线上一动点,在x轴上是否存在点N,使以点B,C,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
21.小丽家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题:
(1)当时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小丽在通电开机后即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的温度约为多少℃?
22.为弘扬向善、为善优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在”的捐款活动,七年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是 ,并补全条形统计图;
(2)请求出本次捐款金额的众数和中位数;
(3)若这所学校七年级学生为1300名,捐款总金额约有多少元?
23.如图,一次函数分别交y轴,x轴于点,将线段向上平移a个单位长度,再向右平移b个单位长度,得到线段,点A的对应点为点C,点B的对应点为点D,反比例函数经过点.
(1)求的数量关系;
(2)若,直接写出反比例函数表达式.
24.如图①,将△ABC绕点A逆时针旋转90°得到△ADE.
(1)DE与BC的位置关系为 ;
(2)如图②,连接CD,BE,若M为BE的中点,连接AM,请探究线段AM与CD的关系,并给予证明;
(3)如图③,已知E是正方形ABCD的边BC上任意一点,以AE为边作正方形AEFG,连接BG,M为BG的中点,连接AM.
①若AB=4,BE=3,求AM的长;
②若AB=a,BE=b,则AM的长为 .(用含a,b的代数式表示)
答案解析部分
1.D
2.A
一元二次方程 有一个根为 0 ,
∴a-1≠0且
∴a≠1且a=±1
∴a=-1
故答案为A.
首先是一元二次方程,所以a-1≠0,再把x=0代入得,解出a的值即可.
3.D
解:A、,
∵,且,
∴,
∴,但无法确定的正负,
∴无法确定的正负,故A不符合题意;
B、,
∵,且,
∴,但无法确定的正负,
∴无法确定的正负,
∴无法确定的正负,故B不符合题意;
C、,
∵,且,
∴,但无法确定的正负,
∴无法确定的正负,
∴无法确定的正负,故C不符合题意;
D、,
∵,且,
∴,
∴,
∴0 ,故D正确;
故答案为:D.
求出,结合条件得,于是得,但无法确定的正负,即可判断A不符合题意;求出,结合条件得,但无法确定的正负,即可判断B不符合题意;求出,结合条件得,但无法确定的正负,即可判断C不符合题意;求出,结合条件得,,即可判断D符合题意.
4.B
解:解:由题意得正六边形每个内角为,六边形MBCDEN的内角和为,
∴,
∴,
∵,
∴,
故答案为:B
先根据正多边形的内角和内角和得到正六边形每个内角为,六边形的内角和为,进而即可得到,从而得到,再根据“”代入化简即可求解。
5.C
6.B
7.B
8.C
9.B
解:∵四边形是边长为的正方形,
∴,,
∴,
由翻折得,,垂直平分,
在和中,
,
∴,
∴,
∴,
∵,
∴,
∵,且,
∴,
解得,
∵,
∴,
解得,
故选:.
由翻折的性质可得,,垂直平分,然后利用“”证明,即可得到,求得,再利用勾股定理求出,再由,求出,再利用三角形的面积求出FH长解题即可.
10.B
解:①若一元二次方程x2+bx+a=0有一个根是-a(a≠0),则a2+b×(-a)+a=0
整理得出:a(a-b+1)=0,则代数式a-b=-1,正确;
②若a+b+c=0,则x=1是一元二次方程ax2+bx+c=0的一个根,不正确;
③若b=2a+3c,那么△=b2-4ac=(2a+3c)2-4ac=(2a+2c)2+5c2,
当a≠0,c=-a时,△>0;当a≠0,c=0时,△>0;当a≠c≠0时,△>0,
∴△>0,正确;
④∵关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0有解,
则m≠0,
∴△≥0
mx2-4x+4=0,
∴△=16-16m≥0,即m≤1;
x2-4mx+4m2-4m-5=0,
△=16m2-16m2+16m+20≥0,
∴4m+5≥0,m≥- ;
∴- ≤m≤1,而m是整数,
所以m=1,m=0(舍去),m=-1(一个为x2-4x+4=0,另一个为x2+4x+3=0,冲突,故舍去),
当m=1时,mx2-4x+4=0即x2-4x+4=0,方程的解是x1=x2=2;
x2-4mx+4m2-4m-5=0即x2-4x-5=0,方程的解是x1=5,x2=-1;
当m=0时,mx2-4x+4=0时,方程是-4x+4=0不是一元二次方程,故舍去.
故m=1,故不符合题意;
故正确的有2个,
故答案为:B.
①根据方程根的定义将x= a代入方程得出a b的值即可;
②利用a+b+c=0,即x=1是一元二次方程ax2+bx+c=0的一个根得出答案,③利用b=2a+3c,算出方程根的判别式的值,分析判别式的值得出即可;
④根据关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0有解,得出根与判别式△≥0,且m≠0,从而列出关于m不等式,求解求得m的范围,再根据m是整数,即可得到m的可能取到的几个值,然后对每个值进行检验,是否符合使两个一元二次方程的解都是整数即可确定m的值,综上所述即可得出答案.
11.
由得故填
考查二次根式有意义条件,由被开方数是非负数得不等式,会解不等式求解,易错点非负数的表示。
12.1
解:∵关于x的一元二次方程 有两个相等的实数根,∴△=0,∴4﹣4m=0,∴m=1。
故答案为:1。
根据一元二次方程根的判别式,由关于x的一元二次方程 有两个相等的实数根得出其根的判别式的值等于0,从而列出方程,求解即可。
13.
14.
解:如图,
连接EF,设AE交BF于点O,
由作图可知:AB=AF,AE平分∠BAD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB=∠EAB,
∴AB=BE,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴AE⊥BF,
∴AO=OE=AE,BO=OF=3,
在Rt△AOB中,AO=,
∴AE=2AO=2.
故答案为:2.
连接EF,设AE交BF于点O,根据一组对边平行且相等的四边形是平行四边形可得四边形ABEF是平行四边形,再根据一组邻边相等的平行四边形是菱形可得四边形ABEF是菱形,在Rt△AOB中,用勾股定理求出AO的值,然后根据菱形的性质得AE=2AO可求解.
15.8
16.(1)2
(2)60
解:(1)根据翻折性质可得,
四边形ABCD是平行四边形,
AB=AE=4,
CE=BC-BE=2,
(2)取AE的中点M,连接DM,DE,如图,
由翻折可知,AD=AF,
M是AE的中点,
DM=EM=AM==DE,
是等边三角形,
故答案为:60.
(1)利用翻折的性质得到再利用平行四边形的性质求得进而得到于是由AB=AE=4,从而求解;
(2)取AE的中点M,连接DM,DE,利用翻折的性质得到AD=AF,利用勾股定理求得DE,AE的值,再证明是等边三角形,进而求解.
17.
解:如图, 作DM∥AC, 使得DM=EF =1, 连接BM交AC于F,
∵DM =EF,DM∥EF,
∴四边形DEFM是平行四边形,
∴DE=FM,
∴DE+BF =FM+FB= BM,根据两点之间线段最短可知,此时DE+FB最短,
∵四边形ABCD是菱形, AB=3, ∠BAD=60°
∴AD=AB,
∴△ABD是等边三角形,
∴BD=AB=3,
在Rt△BDM中,
∴DE+BF的最小值为
故答案为
作DM∥AC, 使得DM = EF= 1, 连接BM交AC于F,由四边形DEFM是平行四边形,推出DE=FM, 推出DE+BF=FM+FB=BM, 根据两点之间线段最短可知,此时DE+FB最短, 由四边形ABCD是菱形, 在Rt△BDM中, 根据 计算即可.
18.
解:连接、,
∵矩形OACB与反比例函数 的图象相交于点E、D,
,
,
又∵ 点的纵坐标为,点的横坐标为,
∴OA=m,OB=,
,
.
故答案为:.
根据反比例函数k的几何意义可得,结合三角形面积计算公式可得,从而代入OA、OB的值,化简整理可得结论.
19.(1)
(2)
20.(1)
(2)解:连接,
∵,
∴,
设的解析式为,
将点,代入,得
,
解得,
∴,
∴的解析式为,
∴,
∴,
∴,
设的解析式为,
将点A、G代入可得
,
解得,
∴;
(3)存在,N点坐标为或或
解:(1)∵面积为10,
∴,
∴,
∵,
∴,
将点B与C的坐标代入,可得
,
∴,
∴,
故答案为,;
(3)∵点M为直线上动点,点N在x轴上,
则可设,,
①当分别为对角线时,
的中点为,的中点为,
∴,,
∴,,
∴;
②当分别为对角线时,
的中点为,的中点为,
∴,,
∴,,
∴;
③当分别为对角线时,
的中点为,的中点为,
∴,,
∴,,
∴;
综上所述:以点B,C,M,N为顶点的四边形为平行四边形时,N点坐标为或或.
(1)根据三角形面积可得AC,再根据两点间距离可得点C坐标,根据待定系数法将点B,C坐标代入解析式即可求出答案.
(2)根据三角形面积可得,设的解析式为,根据待定系数法将点A,B坐标代入解析式可得,根据直线平行性质可得的解析式为,联立两直线方程可得,设的解析式为,根据待定系数法将点A,G坐标代入解析式即可求出答案.
(3)设,,分情况讨论:①当分别为对角线时,②当分别为对角线时,③当分别为对角线时,根据线段中点建立方程,解方程即可求出答案.
21.(1)解:当时,设.
将点,代入上式,
得,解得.
(2)解:当时,设,
将点代入上式,
得,解得,
,
将点代入,
得,解得.
(3)解:由题可知,开机分钟与开机分钟时饮水机的水温相等,
当时,.
小丽散步分钟回到家时,饮水机内的温度约为.
(1)利用待定系数法求一次函数解析式,即可;
(2)利用待定系数法求反比例函数解析式,再将代入解析式,即可得的值;
(3)利用已知由x=20代入求出饮水机内的水的温度即可.
22.(1)50
(2)15,15
(3)17420元
23.(1)
(2)
24.(1);
(2),,
(3)①;②.
同课章节目录
