第二十七章 反比例函数 单元测试(含详解)冀教版数学九年级上册
文档属性
| 名称 | 第二十七章 反比例函数 单元测试(含详解)冀教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 291.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-19 00:00:00 | ||
图片预览


文档简介
第二十七章反比例函数
综合素质评价
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.下列函数中,y是x的反比例函数的是( )
A.y=x B.y=2x-3
C.xy=-3 D.y=
2.若点A(1,3)在反比例函数y=的图像上,则k的值是( )
A.1 B.2 C.3 D.4
3.反比例函数y=的图像在( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
4.下列各点中,在反比例函数y=的图像上的是( )
A.(-1,8) B.(-2,4)
C.(1,7) D.(2,4)
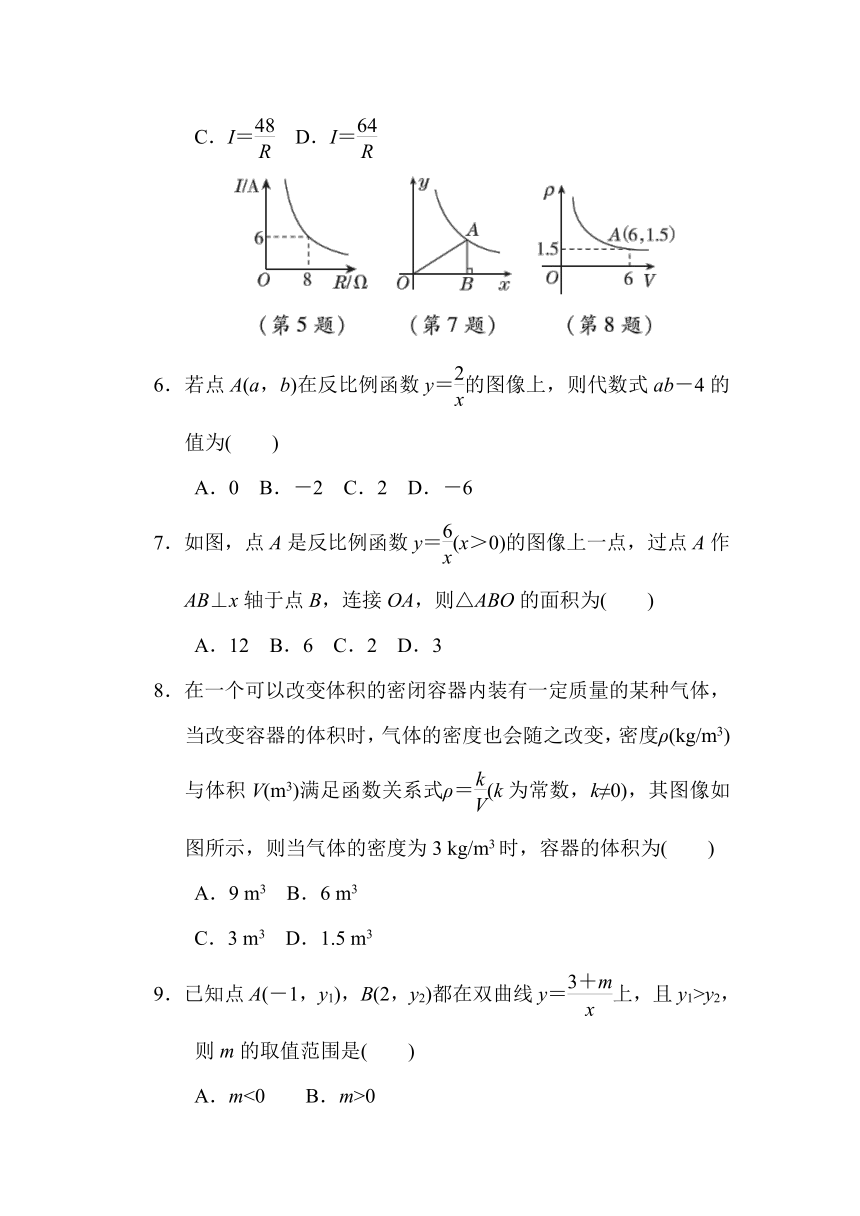
5.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图像如图所示,则这个反比例函数的表达式为( )
A.I= B.I=
C.I= D.I=
6.若点A(a,b)在反比例函数y=的图像上,则代数式ab-4的值为( )
A.0 B.-2 C.2 D.-6
7.如图,点A是反比例函数y=(x>0)的图像上一点,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A.12 B.6 C.2 D.3
8.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(kg/m3)与体积V(m3)满足函数关系式ρ=(k为常数,k≠0),其图像如图所示,则当气体的密度为3 kg/m3时,容器的体积为( )
A.9 m3 B.6 m3
C.3 m3 D.1.5 m3
9.已知点A(-1,y1),B(2,y2)都在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0
C.m>-3 D.m<-3
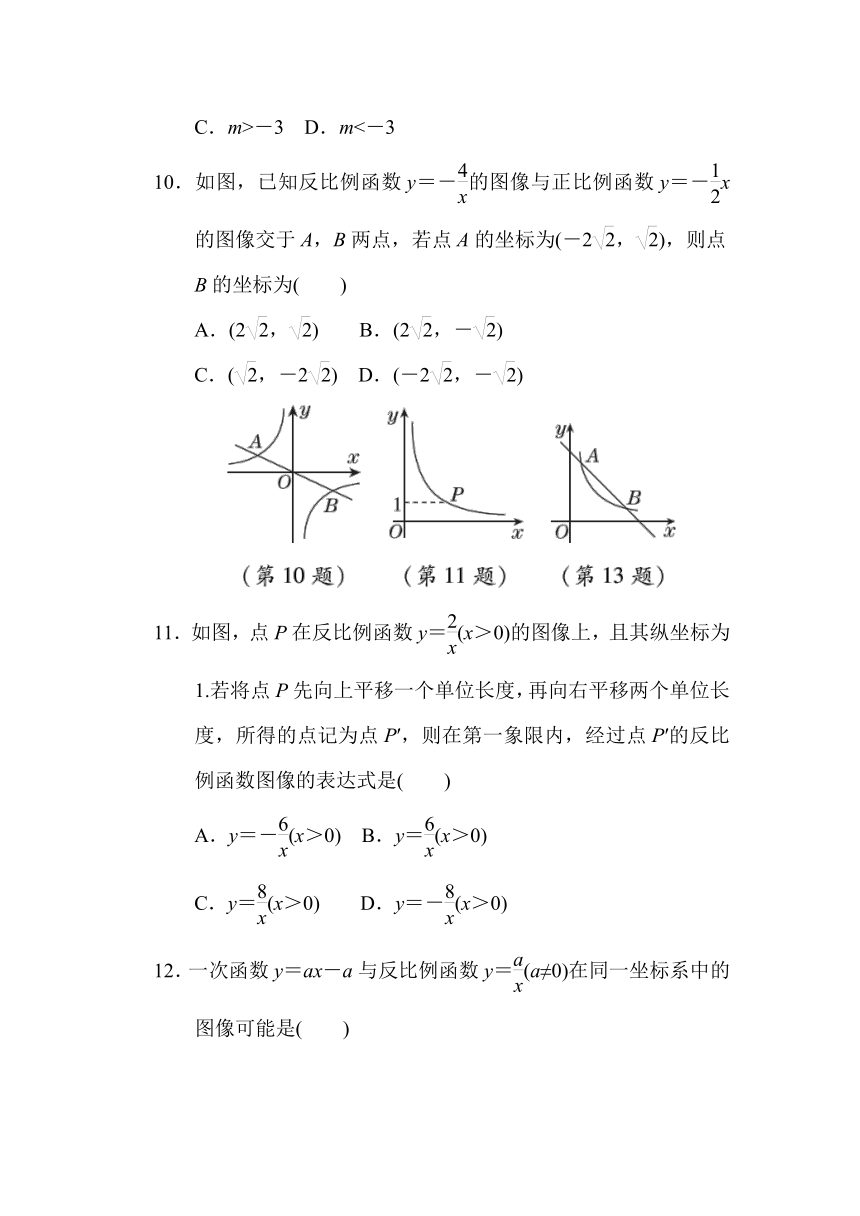
10.如图,已知反比例函数y=-的图像与正比例函数y=-x的图像交于A,B两点,若点A的坐标为(-2,),则点B的坐标为( )
A.(2,) B.(2,-)
C.(,-2) D.(-2,-)
11.如图,点P在反比例函数y=(x>0)的图像上,且其纵坐标为1.若将点P先向上平移一个单位长度,再向右平移两个单位长度,所得的点记为点P′,则在第一象限内,经过点P′的反比例函数图像的表达式是( )
A.y=-(x>0) B.y=(x>0)
C.y=(x>0) D.y=-(x>0)
12.一次函数y=ax-a与反比例函数y=(a≠0)在同一坐标系中的图像可能是( )
13.如图,在直角坐标系中,直线y=6-x与函数y=(x>0)的图像相交于点A,B,设点A的坐标为(x1,y1),那么长为y1、宽为x1的矩形的面积和周长分别为( )
A.4,12 B.8,12 C.4,6 D.8,6
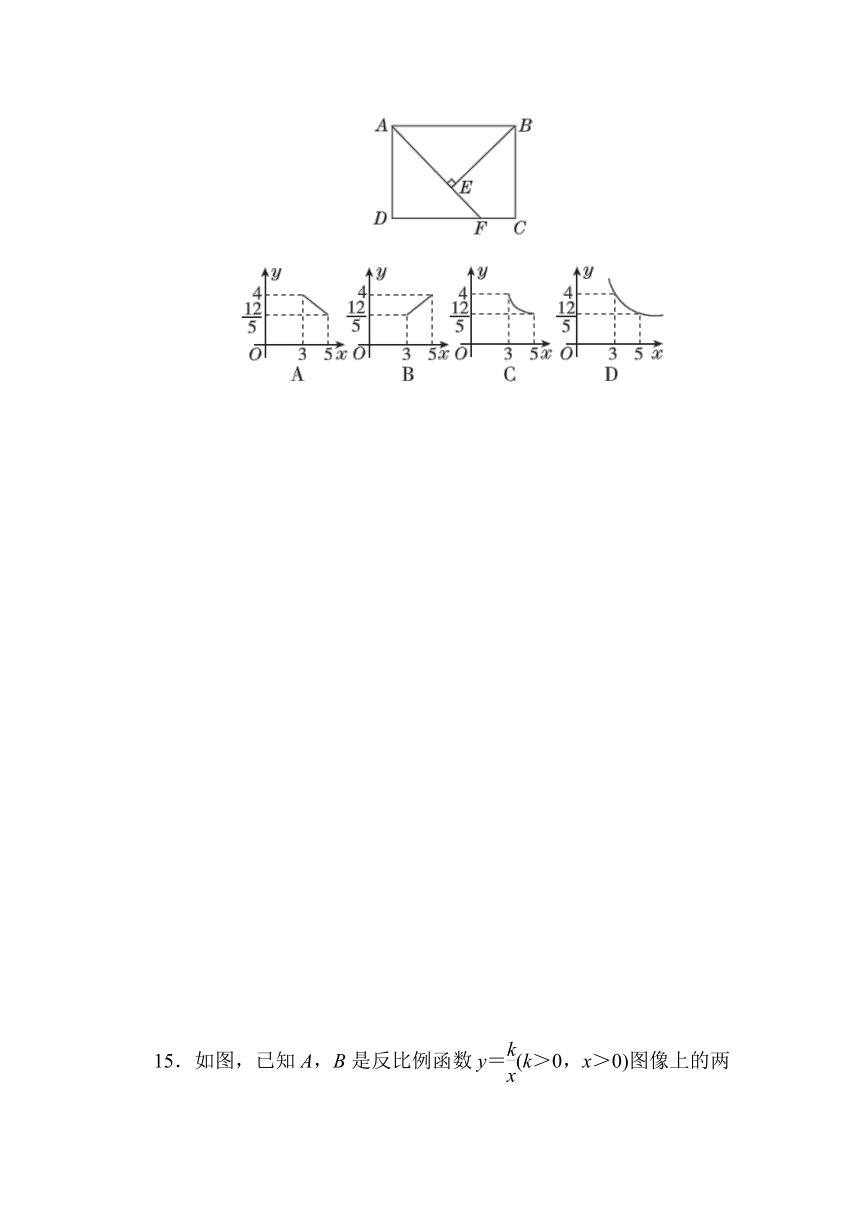
14.如图,在矩形ABCD中,AB=4,BC=3,点F在DC边上运动,连接AF,过点B作BE⊥AF于E.设BE=y,AF=x,则能反映y与x之间函数关系的大致图像是( )
15.如图,已知A,B是反比例函数y=(k>0,x>0)图像上的两点,BC∥y轴,交x轴于点C.动点P从点A出发,沿A→B→C匀速运动,终点为C,过点P作PQ⊥x轴于点Q.设△OPQ的面积为S,点P运动的时间为t,则S关于t的函数图像大致为( )
16.如图,点A在双曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,AB∥x轴,点C是x轴上一点,连接AC,BC.若△ABC的面积是6,则k的值是( )
A.-6 B.-8
C.-10 D.-12
二、填空题(17题3分,18,19题每题4分,共11分)
17.如图,矩形ABCD的顶点A,D在y轴上,顶点C在第一象限,x轴为该矩形的一条对称轴,且矩形ABCD的面积为6.若反比例函数y=的图像经过点C,则k的值为________.
18.若A(1,y1),B(3,y2)是反比例函数y=图像上的两点,则y1,y2的大小关系是y1________y2(填“>”“=”或“<”).
19.如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若经过点C的反比例函数图像的表达式是y=,则经过点D的反比例函数的表达式是____________.
三、解答题(20,21题每题10分,22~24题每题11分,25题14分,共67分)
20.已知y与x-1成反比例,且当x=-5时,y=2.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
21.已知反比例函数y=.(m为常数)
(1)若该函数图像经过点A(1,4),求m的值;
(2)当x>0时,y随x的增大而增大,求m的取值范围.
22.如图,点A(m,4)在反比例函数y=(x>0)的图像上,点B在y轴上,OB=2,将线段AB向右下方平移,得到线段CD,此时点C落在反比例函数的图像上,点D落在x轴正半轴上,且OD=1.
(1)点B的坐标为________,点D的坐标为________,点C的坐标为________(用含m的式子表示);
(2)求k的值和直线AC的表达式.
23.某电厂有5 000 t电煤.请回答下列问题:
(1)求这些电煤能够使用的时长y(单位:天)与该电厂平均每天的用煤量x(单位:t)之间的函数关系式.
(2)若平均每天用煤200 t,则这些电煤能用多少天?
(3)若该电厂前10天每天用煤200 t,后来因各地用电紧张,每天用煤300 t,则这些电煤一共可用多少天?
24.某校“绿色环保”研究性学习小组对部分室内装修队使用劣质油漆进行装修的居室进行调查研究.调查显示,居室内有油漆中挥发的某种有毒气体,进一步研究得知:使用劣质油漆装修期间,室内每立方米空气中该种有毒气体含量y(mg)与时间x(天)成正比例.装修后,y与x成反比例.如图所示,现测得某户15天装修完,此时室内每立方米空气中含有该种有毒气体量为9 mg.请根据题中所提供的信息解答下列各问题:
(1)求装修期间y与x之间的函数关系式及自变量x的取值范围.
(2)根据专家介绍,当室内每立方米空气含有该种有毒气体量低于2.7 mg时,方可入住.该住户装修后30天,经考察,室内已无刺鼻气味,此时搬入居住是否妥当?如果不妥,那么装修后至少需要经过多少天方可入住?
25.如图,一次函数y=kx+b的图像与反比例函数y=的图像相交于A(-1,n),B(2,-1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的表达式.
(2)若点D与点C关于x轴对称,求△ABD的面积.
(3)若M(x1,y1),N(x2,y2)是反比例函数y=图像上的两点,当x1<x2<0时,比较y1与y2的大小关系.
答案
一、1.C
2.C 【点拨】∵点A(1,3)在反比例函数y=的图像上,
∴k=1×3=3,故选C.
3.B 【点拨】∵反比例函数y=中,k=2>0,
∴此函数图像的两个分支分别位于一、三象限.故选B.
4.D 【点拨】A.∵-1×8=-8≠8,∴该点不在函数图像上,故本选项不合题意;
B.∵-2×4=-8≠8,∴该点不在函数图像上,故本选项不合题意;
C.∵1×7=7≠8,∴该点不在函数图像上,故本选项不合题意;
D.2×4=8,∴该点在函数图像上,故本选项符合题意.
故选:D.
5.C 【点拨】设I=,∵图像过点(8,6),∴k=8×6=48,故这个反比例函数的表达式为:I=.
故选C.
6.B 【点拨】∵点A(a,b)在反比例函数y=的图像上,∴b=,即ab=2,∴原式=2-4=-2.
故选B.
7.D 【点拨】设A(a,b),则OB=a,AB=b,∵A为反比例函数y=(x>0)图像上一点,
∴ab=6,∴S△ABO=AB·OB=ab=×6=3,故选:D.
8.C 【点拨】由图像可知,函数图像经过点A(6,1.5),将点A(6,1.5)的坐标代入函数关系式ρ=,
则1.5=,解得k=9,∴ρ=,当ρ=3时,V=3,
故选C.
9.D 【点拨】将A(-1,y1),B(2,y2)两点的坐标分别代入y=,得y1=-3-m,y2=,
∵y1>y2,∴-3-m>,解得m<-3,故选:D.
10.B 【点拨】根据函数图像的对称性,可知点A的横坐标和点B的横坐标互为相反数;点A的纵坐标和点B的纵坐标互为相反数,∵A(-2,),∴B(2,-),故选B.
11.C 【点拨】由点P在y=(x>0)的图像上,且纵坐标为1,可知其横坐标为2,易得P′(4,2),设P′在函数y=(x>0)的图像上,则k=8,所以所求函数图像的表达式为y=(x>0).故选C.
12.D 【点拨】A.由函数y=ax-a的图像可得出a>0,同时-a>0两个结论,矛盾,错误;
B.由函数y=ax-a的图像可知a<0,由函数y=(a≠0)的图像可知a>0,矛盾,错误;
C.由函数y=ax-a的图像可知a>0,由函数y=(a≠0)的图像可知a<0,矛盾,故错误;
D.由函数y=ax-a的图像可知a<0,由函数y=(a≠0)的图像可知a<0,故正确.
13.A 【点拨】由反比例函数y=(k≠0)中的比例系数k的几何意义可知矩形的面积为|k|,即为4.
∵A(x1,y1)在第一象限,即x1>0,y1>0,由直线y=6-x得x1+y1=6,
∴矩形的周长为2(x1+y1)=12.
14.C 【点拨】连接BF,则可知S△AFB=xy=×4×3,故y=,其自变量的取值范围是3≤x≤5,对应的函数值的取值范围为≤y≤4,故选C.
15.A 【点拨】①点P在AB上运动时,此时△OPQ的面积不变;②点P在BC上运动时,S是t的一次函数,且S随着t的增大而减小.故选A.
16.C 【点拨】如图,连接OA,OB,设AB与y轴交于点M.
∵AB∥x轴,点A在双曲线y1=(x>0)上,
点B在双曲线y2=(x<0)上,
∴S△AOM=×|2|=1,S△BOM=×|k|=-k.
易得S△ABC=S△AOB=6,∴1-k=6.
∴k=-10.
二、17.3 【点拨】设BC交x轴于E,如图:
∵x轴为矩形ABCD的一条对称轴,且矩形ABCD的面积为6,∴四边形DOEC是矩形,且矩形DOEC面积是3.点C在反比例函数y=的图像上,根据k的几何意义,及图像所在象限,即可得出k=3.
18.< 【点拨】∵m<,∴2m-1<0,∴图像位于第二、四象限,在每一个象限内,y随x的增大而增大,又∵0<1<3,∴y1<y2.
19.y=- 【点拨】如图,过点C作CT⊥y轴于点T,过点D作DH⊥CT交CT的延长线于点H.
∵tan∠ABO==3,∴可以假设OB=a,OA=3a,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠AOB=∠BTC=90°,
∴∠ABO+∠CBT=90°,∠CBT+∠BCT=90°,
∴∠ABO=∠BCT,∴△AOB≌△BTC(AAS),∴BT=OA=3a,OB=TC=a,∴OT=BT-OB=2a,
∴C(a,2a),∵点C在y=的图像上,∴2a2=1,同法可证△CHD≌△BTC,
∴DH=CT=a,CH=BT=3a,∴D(-2a,3a),设经过点D的反比例函数图像的表达式为y=,则有-2a·3a=k,∴k=-6a2=-3,∴经过点D的反比例函数图像的表达式是y=-.
三、20.【解】(1)设y与x-1的函数关系式为y=,
由题意得2=,解得k=-12.
∴y与x的函数关系式为y=-.
(2)当x=5时,y=-=-=-3.
21.【解】(1)把点A(1,4)的坐标代入y=中,
得4=,解得m=11.
(2)由题意,得m-7<0,∴m<7.
22.【解】(1)(0,2);(1,0);(m+1,2)
(2)∵点A和点C在反比例函数y=的图像上,
∴k=4m=2(m+1),解得m=1.
∴A(1,4),C(2,2),k=1×4=4.
设直线AC的表达式为y=ax+b.
将A(1,4),C(2,2)的坐标分别代入,得
解得
∴直线AC的表达式为y=-2x+6.
23.【解】(1)由题意可得y=.
(2)把x=200代入y=,得y=25.
故这些电煤能用25天.
(3)前10天共用电煤10×200=2 000(t),还剩电煤5 000-2 000=3 000(t),
还可以使用=10(天),
10+10=20(天).
故这些电煤一共可用20天.
24.【解】(1)设装修期间y与x之间的函数关系式为y=k1x(k1≠0),
∵点(15,9)在直线y=k1x上,∴15k1=9.
∴k1=.∴装修期间y与x之间的函数关系式为y=x(0≤x≤15).
(2)设装修后y与x之间的函数关系式为y=(k2≠0).
∵点(15,9)在反比例函数y= (k2≠0)的图像上,
∴9=.∴k2=135.
∴装修后y与x之间的函数关系式为y=(x>15).
装修后30天,即x=45.
当x=45时,y==3>2.7.
∴该住户在装修后30天搬入居住不妥.
当y=2.7时,即2.7=,解得x=50.
50-15=35(天).
∴装修后至少需要经过35天方可入住.
25.【解】(1)∵反比例函数y=的图像经过点B(2,-1),
∴m=-2.
∴反比例函数的表达式为y=-.
∵点A(-1,n)在y=-的图像上,
∴n=-=2.
∴点A的坐标为(-1,2).
把A,B的坐标分别代入y=kx+b,得
解得
∴一次函数的表达式为y=-x+1.
(2)∵直线y=-x+1交y轴于点C,
∴点C的坐标为(0,1).
∵点D,C关于x轴对称,∴点D的坐标为(0,-1).
又∵点B的坐标为(2,-1),∴BD∥x轴,BD=2.
∴S△ABD=×2×[2-(-1)]=3.
(3)∵M(x1,y1),N(x2,y2)是反比例函数y=-图像上的两点,且x1<x2<0,∴y1<y2.
综合素质评价
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.下列函数中,y是x的反比例函数的是( )
A.y=x B.y=2x-3
C.xy=-3 D.y=
2.若点A(1,3)在反比例函数y=的图像上,则k的值是( )
A.1 B.2 C.3 D.4
3.反比例函数y=的图像在( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
4.下列各点中,在反比例函数y=的图像上的是( )
A.(-1,8) B.(-2,4)
C.(1,7) D.(2,4)
5.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图像如图所示,则这个反比例函数的表达式为( )
A.I= B.I=
C.I= D.I=
6.若点A(a,b)在反比例函数y=的图像上,则代数式ab-4的值为( )
A.0 B.-2 C.2 D.-6
7.如图,点A是反比例函数y=(x>0)的图像上一点,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A.12 B.6 C.2 D.3
8.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(kg/m3)与体积V(m3)满足函数关系式ρ=(k为常数,k≠0),其图像如图所示,则当气体的密度为3 kg/m3时,容器的体积为( )
A.9 m3 B.6 m3
C.3 m3 D.1.5 m3
9.已知点A(-1,y1),B(2,y2)都在双曲线y=上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0
C.m>-3 D.m<-3
10.如图,已知反比例函数y=-的图像与正比例函数y=-x的图像交于A,B两点,若点A的坐标为(-2,),则点B的坐标为( )
A.(2,) B.(2,-)
C.(,-2) D.(-2,-)
11.如图,点P在反比例函数y=(x>0)的图像上,且其纵坐标为1.若将点P先向上平移一个单位长度,再向右平移两个单位长度,所得的点记为点P′,则在第一象限内,经过点P′的反比例函数图像的表达式是( )
A.y=-(x>0) B.y=(x>0)
C.y=(x>0) D.y=-(x>0)
12.一次函数y=ax-a与反比例函数y=(a≠0)在同一坐标系中的图像可能是( )
13.如图,在直角坐标系中,直线y=6-x与函数y=(x>0)的图像相交于点A,B,设点A的坐标为(x1,y1),那么长为y1、宽为x1的矩形的面积和周长分别为( )
A.4,12 B.8,12 C.4,6 D.8,6
14.如图,在矩形ABCD中,AB=4,BC=3,点F在DC边上运动,连接AF,过点B作BE⊥AF于E.设BE=y,AF=x,则能反映y与x之间函数关系的大致图像是( )
15.如图,已知A,B是反比例函数y=(k>0,x>0)图像上的两点,BC∥y轴,交x轴于点C.动点P从点A出发,沿A→B→C匀速运动,终点为C,过点P作PQ⊥x轴于点Q.设△OPQ的面积为S,点P运动的时间为t,则S关于t的函数图像大致为( )
16.如图,点A在双曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,AB∥x轴,点C是x轴上一点,连接AC,BC.若△ABC的面积是6,则k的值是( )
A.-6 B.-8
C.-10 D.-12
二、填空题(17题3分,18,19题每题4分,共11分)
17.如图,矩形ABCD的顶点A,D在y轴上,顶点C在第一象限,x轴为该矩形的一条对称轴,且矩形ABCD的面积为6.若反比例函数y=的图像经过点C,则k的值为________.
18.若A(1,y1),B(3,y2)是反比例函数y=图像上的两点,则y1,y2的大小关系是y1________y2(填“>”“=”或“<”).
19.如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若经过点C的反比例函数图像的表达式是y=,则经过点D的反比例函数的表达式是____________.
三、解答题(20,21题每题10分,22~24题每题11分,25题14分,共67分)
20.已知y与x-1成反比例,且当x=-5时,y=2.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
21.已知反比例函数y=.(m为常数)
(1)若该函数图像经过点A(1,4),求m的值;
(2)当x>0时,y随x的增大而增大,求m的取值范围.
22.如图,点A(m,4)在反比例函数y=(x>0)的图像上,点B在y轴上,OB=2,将线段AB向右下方平移,得到线段CD,此时点C落在反比例函数的图像上,点D落在x轴正半轴上,且OD=1.
(1)点B的坐标为________,点D的坐标为________,点C的坐标为________(用含m的式子表示);
(2)求k的值和直线AC的表达式.
23.某电厂有5 000 t电煤.请回答下列问题:
(1)求这些电煤能够使用的时长y(单位:天)与该电厂平均每天的用煤量x(单位:t)之间的函数关系式.
(2)若平均每天用煤200 t,则这些电煤能用多少天?
(3)若该电厂前10天每天用煤200 t,后来因各地用电紧张,每天用煤300 t,则这些电煤一共可用多少天?
24.某校“绿色环保”研究性学习小组对部分室内装修队使用劣质油漆进行装修的居室进行调查研究.调查显示,居室内有油漆中挥发的某种有毒气体,进一步研究得知:使用劣质油漆装修期间,室内每立方米空气中该种有毒气体含量y(mg)与时间x(天)成正比例.装修后,y与x成反比例.如图所示,现测得某户15天装修完,此时室内每立方米空气中含有该种有毒气体量为9 mg.请根据题中所提供的信息解答下列各问题:
(1)求装修期间y与x之间的函数关系式及自变量x的取值范围.
(2)根据专家介绍,当室内每立方米空气含有该种有毒气体量低于2.7 mg时,方可入住.该住户装修后30天,经考察,室内已无刺鼻气味,此时搬入居住是否妥当?如果不妥,那么装修后至少需要经过多少天方可入住?
25.如图,一次函数y=kx+b的图像与反比例函数y=的图像相交于A(-1,n),B(2,-1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的表达式.
(2)若点D与点C关于x轴对称,求△ABD的面积.
(3)若M(x1,y1),N(x2,y2)是反比例函数y=图像上的两点,当x1<x2<0时,比较y1与y2的大小关系.
答案
一、1.C
2.C 【点拨】∵点A(1,3)在反比例函数y=的图像上,
∴k=1×3=3,故选C.
3.B 【点拨】∵反比例函数y=中,k=2>0,
∴此函数图像的两个分支分别位于一、三象限.故选B.
4.D 【点拨】A.∵-1×8=-8≠8,∴该点不在函数图像上,故本选项不合题意;
B.∵-2×4=-8≠8,∴该点不在函数图像上,故本选项不合题意;
C.∵1×7=7≠8,∴该点不在函数图像上,故本选项不合题意;
D.2×4=8,∴该点在函数图像上,故本选项符合题意.
故选:D.
5.C 【点拨】设I=,∵图像过点(8,6),∴k=8×6=48,故这个反比例函数的表达式为:I=.
故选C.
6.B 【点拨】∵点A(a,b)在反比例函数y=的图像上,∴b=,即ab=2,∴原式=2-4=-2.
故选B.
7.D 【点拨】设A(a,b),则OB=a,AB=b,∵A为反比例函数y=(x>0)图像上一点,
∴ab=6,∴S△ABO=AB·OB=ab=×6=3,故选:D.
8.C 【点拨】由图像可知,函数图像经过点A(6,1.5),将点A(6,1.5)的坐标代入函数关系式ρ=,
则1.5=,解得k=9,∴ρ=,当ρ=3时,V=3,
故选C.
9.D 【点拨】将A(-1,y1),B(2,y2)两点的坐标分别代入y=,得y1=-3-m,y2=,
∵y1>y2,∴-3-m>,解得m<-3,故选:D.
10.B 【点拨】根据函数图像的对称性,可知点A的横坐标和点B的横坐标互为相反数;点A的纵坐标和点B的纵坐标互为相反数,∵A(-2,),∴B(2,-),故选B.
11.C 【点拨】由点P在y=(x>0)的图像上,且纵坐标为1,可知其横坐标为2,易得P′(4,2),设P′在函数y=(x>0)的图像上,则k=8,所以所求函数图像的表达式为y=(x>0).故选C.
12.D 【点拨】A.由函数y=ax-a的图像可得出a>0,同时-a>0两个结论,矛盾,错误;
B.由函数y=ax-a的图像可知a<0,由函数y=(a≠0)的图像可知a>0,矛盾,错误;
C.由函数y=ax-a的图像可知a>0,由函数y=(a≠0)的图像可知a<0,矛盾,故错误;
D.由函数y=ax-a的图像可知a<0,由函数y=(a≠0)的图像可知a<0,故正确.
13.A 【点拨】由反比例函数y=(k≠0)中的比例系数k的几何意义可知矩形的面积为|k|,即为4.
∵A(x1,y1)在第一象限,即x1>0,y1>0,由直线y=6-x得x1+y1=6,
∴矩形的周长为2(x1+y1)=12.
14.C 【点拨】连接BF,则可知S△AFB=xy=×4×3,故y=,其自变量的取值范围是3≤x≤5,对应的函数值的取值范围为≤y≤4,故选C.
15.A 【点拨】①点P在AB上运动时,此时△OPQ的面积不变;②点P在BC上运动时,S是t的一次函数,且S随着t的增大而减小.故选A.
16.C 【点拨】如图,连接OA,OB,设AB与y轴交于点M.
∵AB∥x轴,点A在双曲线y1=(x>0)上,
点B在双曲线y2=(x<0)上,
∴S△AOM=×|2|=1,S△BOM=×|k|=-k.
易得S△ABC=S△AOB=6,∴1-k=6.
∴k=-10.
二、17.3 【点拨】设BC交x轴于E,如图:
∵x轴为矩形ABCD的一条对称轴,且矩形ABCD的面积为6,∴四边形DOEC是矩形,且矩形DOEC面积是3.点C在反比例函数y=的图像上,根据k的几何意义,及图像所在象限,即可得出k=3.
18.< 【点拨】∵m<,∴2m-1<0,∴图像位于第二、四象限,在每一个象限内,y随x的增大而增大,又∵0<1<3,∴y1<y2.
19.y=- 【点拨】如图,过点C作CT⊥y轴于点T,过点D作DH⊥CT交CT的延长线于点H.
∵tan∠ABO==3,∴可以假设OB=a,OA=3a,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠AOB=∠BTC=90°,
∴∠ABO+∠CBT=90°,∠CBT+∠BCT=90°,
∴∠ABO=∠BCT,∴△AOB≌△BTC(AAS),∴BT=OA=3a,OB=TC=a,∴OT=BT-OB=2a,
∴C(a,2a),∵点C在y=的图像上,∴2a2=1,同法可证△CHD≌△BTC,
∴DH=CT=a,CH=BT=3a,∴D(-2a,3a),设经过点D的反比例函数图像的表达式为y=,则有-2a·3a=k,∴k=-6a2=-3,∴经过点D的反比例函数图像的表达式是y=-.
三、20.【解】(1)设y与x-1的函数关系式为y=,
由题意得2=,解得k=-12.
∴y与x的函数关系式为y=-.
(2)当x=5时,y=-=-=-3.
21.【解】(1)把点A(1,4)的坐标代入y=中,
得4=,解得m=11.
(2)由题意,得m-7<0,∴m<7.
22.【解】(1)(0,2);(1,0);(m+1,2)
(2)∵点A和点C在反比例函数y=的图像上,
∴k=4m=2(m+1),解得m=1.
∴A(1,4),C(2,2),k=1×4=4.
设直线AC的表达式为y=ax+b.
将A(1,4),C(2,2)的坐标分别代入,得
解得
∴直线AC的表达式为y=-2x+6.
23.【解】(1)由题意可得y=.
(2)把x=200代入y=,得y=25.
故这些电煤能用25天.
(3)前10天共用电煤10×200=2 000(t),还剩电煤5 000-2 000=3 000(t),
还可以使用=10(天),
10+10=20(天).
故这些电煤一共可用20天.
24.【解】(1)设装修期间y与x之间的函数关系式为y=k1x(k1≠0),
∵点(15,9)在直线y=k1x上,∴15k1=9.
∴k1=.∴装修期间y与x之间的函数关系式为y=x(0≤x≤15).
(2)设装修后y与x之间的函数关系式为y=(k2≠0).
∵点(15,9)在反比例函数y= (k2≠0)的图像上,
∴9=.∴k2=135.
∴装修后y与x之间的函数关系式为y=(x>15).
装修后30天,即x=45.
当x=45时,y==3>2.7.
∴该住户在装修后30天搬入居住不妥.
当y=2.7时,即2.7=,解得x=50.
50-15=35(天).
∴装修后至少需要经过35天方可入住.
25.【解】(1)∵反比例函数y=的图像经过点B(2,-1),
∴m=-2.
∴反比例函数的表达式为y=-.
∵点A(-1,n)在y=-的图像上,
∴n=-=2.
∴点A的坐标为(-1,2).
把A,B的坐标分别代入y=kx+b,得
解得
∴一次函数的表达式为y=-x+1.
(2)∵直线y=-x+1交y轴于点C,
∴点C的坐标为(0,1).
∵点D,C关于x轴对称,∴点D的坐标为(0,-1).
又∵点B的坐标为(2,-1),∴BD∥x轴,BD=2.
∴S△ABD=×2×[2-(-1)]=3.
(3)∵M(x1,y1),N(x2,y2)是反比例函数y=-图像上的两点,且x1<x2<0,∴y1<y2.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
