9.1图形的旋转同步强化练习(含解析)
图片预览
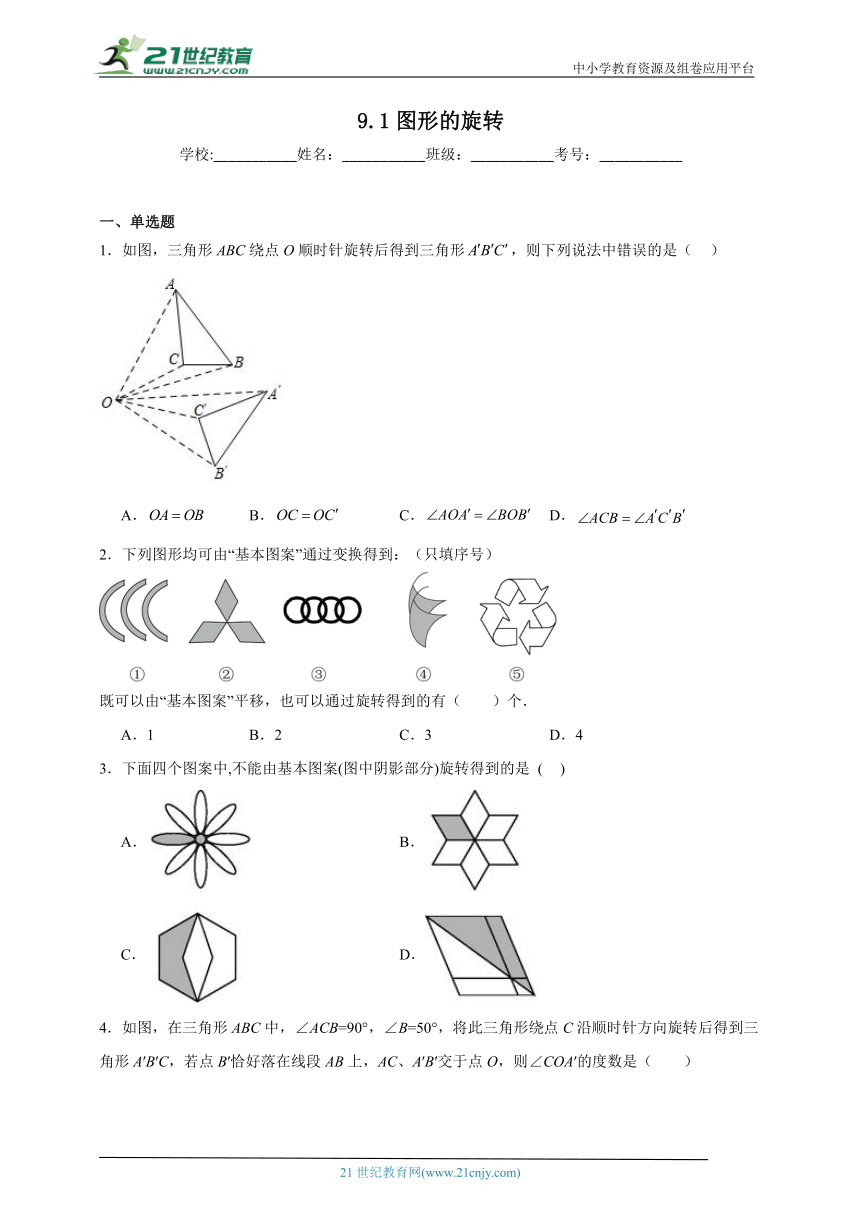


文档简介
中小学教育资源及组卷应用平台
9.1图形的旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,三角形ABC绕点O顺时针旋转后得到三角形,则下列说法中错误的是( )
A. B. C. D.
2.下列图形均可由“基本图案”通过变换得到:(只填序号)
既可以由“基本图案”平移,也可以通过旋转得到的有( )个.
A.1 B.2 C.3 D.4
3.下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是 ( )
A. B.
C. D.
4.如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
A.50° B.60° C.70° D.80°
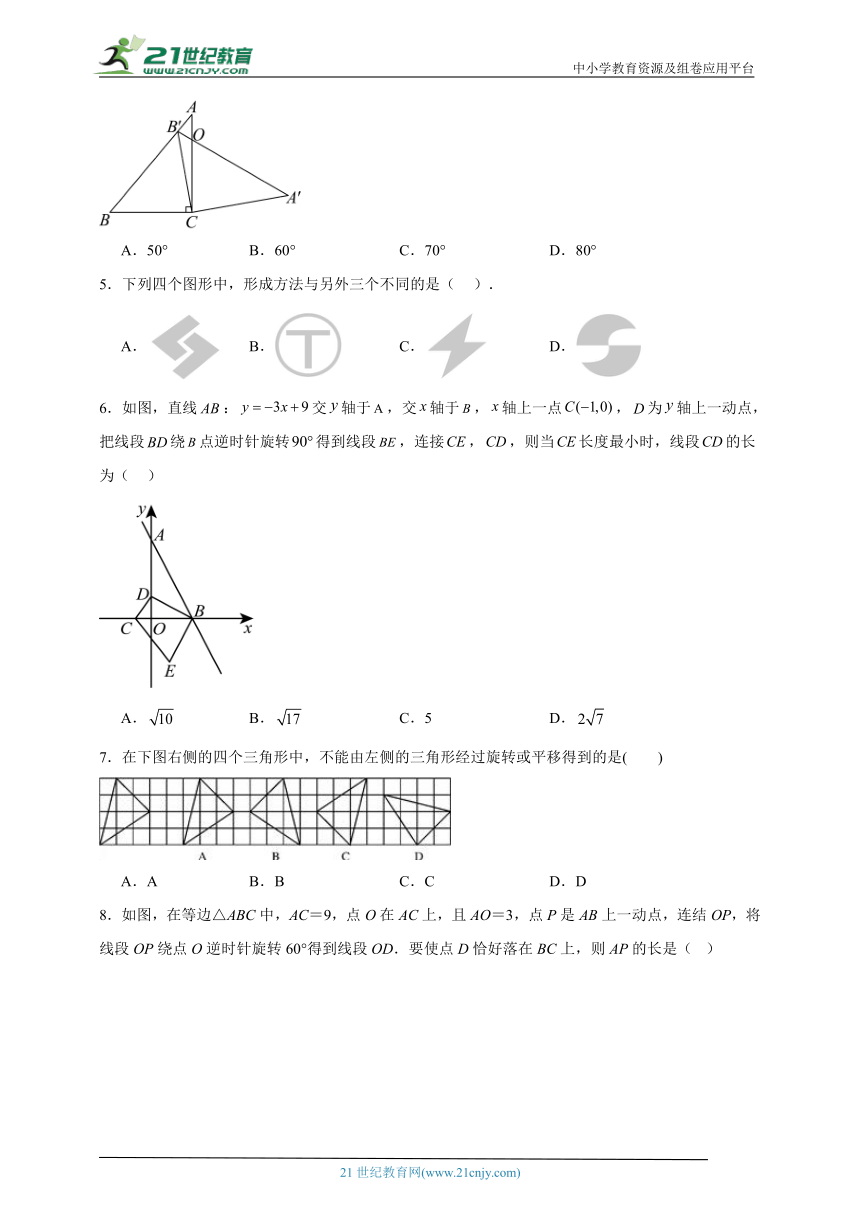
5.下列四个图形中,形成方法与另外三个不同的是( ).
A. B. C. D.
6.如图,直线:交轴于,交轴于,轴上一点,为轴上一动点,把线段绕点逆时针旋转得到线段,连接,,则当长度最小时,线段的长为( )
A. B. C.5 D.
7.在下图右侧的四个三角形中,不能由左侧的三角形经过旋转或平移得到的是( )
A.A B.B C.C D.D
8.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是( )
A.2 B.3 C.5 D.6
9.在中,,点D为中点,,绕点D旋转,分别与边交于E,F两点.下列结论:①;②;③;④始终为等腰直角三角形,其中正确的个数有( ).
A.1个 B.2个 C.3个 D.4个
10.如图,在的正方形网格中,由旋转得到,其旋转中心是( )
A.点 B.点 C.点 D.点
11.一个图形经过旋转变换,下列说法中:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有改变.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
12.如图,将三角形ABC绕着点C顺时针旋转60°后得到三角形A′B′C,若∠A=40°,∠B=110°,则∠A′CB′的度数是( )
A. B. C. D.
二、填空题
13.如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为 .
14.等边绕其外心旋转,至少要旋转 度才能与原图形重合.
15.有如图,从图形甲到图形乙,所进行的图形运动是先绕点 时针旋转,再向右移动 格.
16.在正方形、长方形、线段、等边三角形和平行四边形这五种图形中,是旋转对称图形不是中心对称图形的是 .
17.正九边形绕它的旋转中心至少旋转 °后才能与原图形重合.
三、解答题
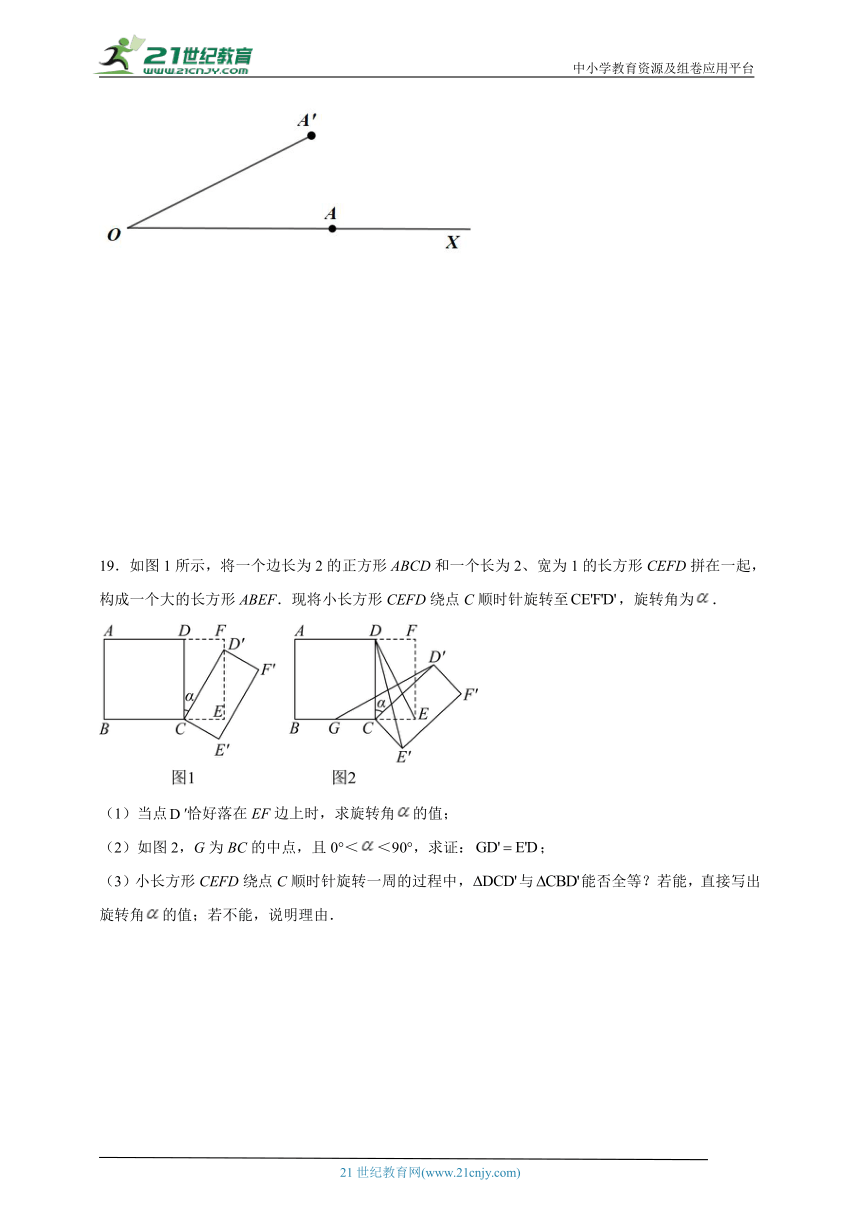
18.如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O,按逆时针方向旋转30°到 ,那么点的位置可以用(2,30°)表示.如果将再沿逆时针方向继续旋转45°,到,那么点的位置可以用( , )表示.
19.如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至,旋转角为.
(1)当点′恰好落在EF边上时,求旋转角的值;
(2)如图2,G为BC的中点,且0°<<90°,求证:;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.
20.如图,点、的坐标分别为、.将绕点按逆时针方向旋转得到.
(1)画出:
(2)写出点、的坐标.
21.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.
(1)问题发现
如图1,△CDE的形状是______三角形.
(2)探究证明
如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
22.如图,中,,,,逆时针旋转一定角度后与重合,且点C恰好成为的中点.
(1)指出能转中心,并求出旋转的度数;
(2)求出的度数和的长.
23.定义:将图形M绕点P顺时针旋转90°得到图形N,则图形N称为图形M关于点P的“垂直图形”.例如:在下图中,点D为点C关于点P的“垂直图形”.
(1)点A关于原点O的“垂直图形”为点B.
①若点A的坐标为(0,2),直接写出点B的坐标;
②若点B的坐标为(2,1),直接写出点A的坐标;
(2)E(-3,3),F(-2,3),G(a,0).线段EF关于点G的“垂直图形”记为E′F′,点E的对应点为E′,点F的对应点为F′.
①求点E′的坐标;
②当点G运动时,求的最小值.
24.在平面直角坐标系中,将坐标为的点用线段依次连接起来得到一个图案N.
(1)将图案N向左平移3个单位长度,画出平移后的图案;
(2)将图案N向下平移4个单位长度,画出平移后的图案;
(3)将图案N先向左平移3个单位长度,再向下平移4个单位长度,画出第二次平移后的图案;
(4)画出图案N关于横轴对称的图案;
(5)画出图案N关于纵轴对称的图案;
(6)以原点为对称中心,画出与图案N成中心对称的图案.
《9.1图形的旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B B B B D D A
题号 11 12
答案 C B
1.A
【分析】根据点O没有条件限定,不一定在AB的垂直平分线上,可判断A,根据性质性质可判断B、C、D.
【详解】解:A.当点O在AB的垂直平分线上时,满足OA=OB,由点O没有限制条件,为此点O为任意的,不一定在AB的垂直平分线上,故选项A不正确,符合题意;
B.由旋转可知OC与OC′是对应线段,由旋转性质可得OC=OC′,故选项B正确,不符合题意;
C.因为、都是旋转角,由旋转性质可得,故选项C正确,不符合题意;
D.由旋转可知与是对应角,由性质性质可得,故选项D正确,不符合题意.
故选择A.
【点睛】本题考查线段垂直平分线性质,图形旋转及其性质,掌握线段垂直平分线性质,图形旋转及其性质是解题关键.
2.A
【分析】此题是一组复合图形,根据平移、旋转的性质解答.
【详解】解:①可以看作由左边图案向右平移得到的;
②可以看作一个菱形绕一个顶点旋转得到的;
③既可以看作一个圆向右平移得到的,也可以看作两个圆组成的图案旋转得到的;
④可以看作上面基本图案向下平移得到的;
⑤可以看作上面图案绕中心旋转得到的.
故可以平移但不能旋转的是①④;
可以旋转但不能平移的是②⑤;
既可以平移,也可以旋转的是③.
故答案为A.
【点睛】本题考查平移、旋转的性质:①平移不改变图形的形状和大小;经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.②旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心,熟练掌握其性质是解决此题的关键.
3.D
【分析】寻找基本图形,旋转中心,旋转角,旋转次数,逐一判断.
【详解】A.可由一个基本花瓣绕其中心经过7次旋转,每次旋转45度得到;
B. 可由一个基本菱形绕其中心经过5次旋转,每次旋转 60度得到;
C. 可由一个基本花瓣绕其中心旋转180度得到;
D. 不能由基本图案旋转得到;
故选D.
【点睛】此题主要考查旋转设计图案.
4.B
【详解】∵在三角形ABC中,∠ACB=90°,∠B=50°,
∴∠A=180°﹣∠ACB﹣∠B=40°.
由旋转的性质可知:BC=B′C,∠OB′C=∠B
∴∠B=∠BB′C=50°.
又∵∠BB′C=∠A+∠ACB′=40°+∠ACB′,
∴∠ACB′=10°,
∴∠COA′=∠AOB′=∠OB′C+∠ACB′=∠B+∠ACB′=60°.
故选B.
【点睛】考点:旋转的性质.
5.B
【分析】本题考查的是旋转与轴对称的性质,利用旋转或轴对称逐一分析各选项即可.
【详解】解:A,C,D选项中的图形都是通过将其中一部分旋转形成的图形,而B选项中的图形是通过轴对称形成的,
故答案为:B
6.B
【分析】作EH⊥x轴于H,通过证明△DBO≌△BEH,可得HE=OB,从而确定点点的运动轨迹是直线,根据垂线段最短确定出点E的位置,然后根据勾股定理求解即可.
【详解】解:作EH⊥x轴于H,
∵∠DBE=90°,
∴∠DBC+∠CBE=90°.
∵∠BHE=90°,
∴∠BEH+∠CBE=90°,
∴∠DBC=∠BEH.
在△DBO和△BEH中,
∵∠DBC=∠BEH,
∠BOD=∠BHE,
BD=BE,
∴△DBO≌△BEH中,
∴HE=OB,
当y=0时,,
∴x=3,
∴HE=OB=3,
∴点的运动轨迹是直线,B(3,0),
∴当⊥m时,CE最短,此时点的坐标为(-1,3),
∵B(-1,0),B(3,0),
∴BC=4,
∴BE′=,
∴BD= BE′=4,
∴OD=,
∴CD=.
故选B.
【点睛】本题考查一次函数与坐标轴的交点,坐标与图形的变化,旋转变换、全等三角形的判定与性质,垂线段最短以及勾股定理等知识,解题的关键是确定点E的位置.
7.B
【详解】试题解析:A、可由△ABC逆时针旋转一个角度得到;
B、可由△ABC翻折得到;
C、可由△ABC逆时针旋转一个角度得到;
D、可由△ABC逆时针旋转一个角度得到.
故选B.
点睛:旋转的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点为旋转中心;②旋转方向;③旋转角度.
8.D
【分析】根据∠A+∠APO=∠POD+∠COD,可得∠APO=∠COD,进而可以证明△APO△COD,进而可以证明AP=CO,即可解题.
【详解】解:∵∠A+∠APO=∠POD+∠COD,∠A=∠POD,
∴∠APO=∠COD,
在△APO和△COD中 ,
∴△APO△COD(AAS),
即AP=CO,
∵CO=AC-AO=6,
∴AP=6.
故答案为6.
【点睛】本题是全等三角形与旋转的综合题型,理解题意,找出全等的三角形,再通过代换求得答案是解题的关键.
9.D
【分析】本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,三角形的面积公式的运用,连接,根据等腰直角三角形的性质就可以得出,就可以得出,进而得出,就有,由勾股定理就即可求出结论.
【详解】解:连接,
,
点D为中点,,
.,.
,
,
.
在和中,
,
,
,.
,
,
.
,
.
,
,
.
,,
始终为等腰直角三角形.
,
.
,
.
∴正确的有4个.
故选:D.
10.A
【分析】本题主要考查了旋转的性质,熟练掌握旋转中心在对应点连线的垂直平分线上是解题的关键.根据旋转的性质可知:旋转中心在对应点连线的垂直平分线上,进而得出答案.
【详解】 解:根据旋转的性质可知:旋转中心在对应点连线的垂直平分线上, 由图形可知:点在的垂直平分线上,又在的垂直平分线上,
∴旋转中心是点,
故选:A.
11.C
【分析】此题考查了旋转的性质,熟练掌握旋转的性质,根据旋转的性质,逐项进行判断即可.
【详解】解:①一个图形经过旋转变换后,对应线段不一定平行,故此说法错误;
②一个图形经过旋转变换后,对应线段相等,故此说法正确;
③一个图形经过旋转变换后,对应角相等,故此说法正确;
④一个图形经过旋转变换后,图形的形状和大小都没有改变,故此说法正确;
综上分析可知,正确的个数为3个.
故选:C.
12.B
【分析】首先根据旋转的性质可得:∠A′=∠A=40°,∠B′=∠B=110°,然后在△B′CA′中利用三角形的内角和定理求解即可.
【详解】解:由旋转的性质可得:∠A′=∠A=40°,∠B′=∠B=110°,
∴∠A′CB′=180°-∠B′-∠A′=180°-110°-40°=30°.
故选:B.
【点睛】本题主要考查的是旋转的性质、三角形的内角和定理,掌握旋转的性质是解题的关键.
13.
【分析】根据已知及勾股定理求得DP的长,再根据全等三角形的判定得到△B′PH≌△BPD,从而根据直角三角形的性质求得GH,BG的长,从而不难求得旋转前后两个直角三角形重叠部分的面积.
【详解】解:设A′B′交BC于D,B′C′交BC于G、交AB于H,
∵∠C=90°,∠A=60°,
∴∠B=30°,
∴AB=2AC=6 ,
在直角△DPB中,BP=AP=AC=3,
设PD=x,
∵∠A=60°,则∠B=30°,
∴BD=2PD=2x,
∵DP2+BP2=BD2,
∴x2+32=(2x)2,
∴DP=x=,
∵B′P=BP,∠B=∠B′,∠B′PH=∠BPD=90°,
∴△B′PH≌△BPD,
∴PH=PD=,
∵在直角△BGH中,BH=3+,
∴GH=BH=,BG=,
∴S△BGH=××=,S△BDP=×3×=,
∴SDGHP=(cm2).
故答案为:.
【点睛】本题考查了勾股定理,三角形的全等的判定及性质,旋转的性质等知识的综合运用.
14.
【分析】根据三角形外形的定义可得垂直平分,结合等边三角形的性质,推出,等边绕其外心旋转与原图形重合,则点A旋转后应与点C重合,求出即可.
【详解】解:如图,点O为的外心,
∴垂直平分,
∵是等边三角形,
∴,平分,
∴,
同理可得的:,
∴,
故答案为:.
【点睛】本题主要考查了等边三角形的性质,旋转的性质,外形的定义,解题的关键是掌握三角形的外心是三角形三条垂直平分线的交点.
15. 逆 10
【分析】根据旋转性质及平移性质即可得到答案.
【详解】解:观察甲乙两图可知,将甲图以为旋转中心,逆时针旋转,再向右平移个单位长度即可得到乙图,
故答案为:逆;.
【点睛】本题考查旋转及平移性质,熟记旋转性质及平移性质作图是解决问题的关键.
16.等边三角形
【分析】根据中心对称图形的定义以及旋转图形的性质分别判断得出即可.
【详解】正方形、长方形、线段、等边三角形和平行四边形这五种图形中、线段和平行四边形和正方形和长方形都是中心对称图形,只有等边三角形是旋转对称图形但不是中心对称图形;故答案为:等边三角形.
【点睛】此题主要考查了旋转图形的性质,注意中心对称图形也属于旋转图形,但要按要求答题
17.40.
【分析】要与原来的九边形重合.可用一个圆周角的度数(即360度)除以9,便可知道至少要旋转多少度才能和原来的五边形重合.
【详解】∵=40°,
故答案为:40.
18.(2,75°)
【分析】根据旋转的性质,旋转不改变图形的大小和形状,即旋转后所得图形与原图形全等,通过分析坐标的形成即可解答.
【详解】解:第一个坐标为原点到此点的距离,旋转前后线段长度不变,所以OA″=OA=2,
第二个坐标为与x轴的夹角=∠A″OA′+∠A′OA=45°+30°=75°,
那么点A”的位置可以用( 2,75°)表示,
故答案为(2,75°).
19.(1)∠α=30°(2)见解析(3)旋转角a的值为135°或315°时,△BCD′与∠DCD′全等
【分析】(1)根据旋转的性质得CE=CH=1,即可得出结论;
(2)由G为BC中点可得CG=CE,根据旋转的性质得∠D′CE′=∠DCE=90°,CE=CE′CE,则∠GCD′=∠DCE′=90°+α,然后根据“SAS”可判断△GCD′≌△E′CD,则GD′=E′D;
(3)根据正方形的性质得CB=CD,而CD=CD′,则△BCD′与△DCD′为腰相等的两等腰三角形,当两顶角相等时它们全等,当△BCD′与△DCD′为钝角三角形时,可计算出α=135°,当△BCD′与△DCD′为锐角三角形时,可计算得到α=315°.
【详解】解:(1)∵长方形CEFD绕点C顺时针旋转至CE′F′D′,
∴CE=CH=1,
∴△CEH为等腰直角三角形,
∴∠ECH=45°,
∴∠α=30°;
(2)证明:∵G为BC中点
∴CG=1
∴CG=CE
∵长方形CEFD绕点C顺时针旋转至CE′F′D′
∴∠D′CE′=∠DCE=90°,CE=CE′=CG
∴∠GCD′=∠DCE′=90°+α
在△GCD′和△E′CD中
∵CD′=CD,∠GCD=∠DCE′,CG=CE′
∴△GCD′≌△E′CD(SAS)
∴GD′=E′D;
(3)解:能.
理由如下:
∵四边形ABCD为正方形
∴CB=CD
∵CD′=CD′
∴△BCD′与△DCD′为腰相等的两等腰三角形,当∠BCD′=∠DCD′时,△BCD′≌△DCD′,当△BCD′与△DCD′为钝角三角形时,则旋转角α=(360°-90°)÷2=135°
当△BCD′与△DCD′为锐角三角形时,∠BCD′=∠DCD′=∠BCD=45°,则α=360°﹣90°÷2=315°
即旋转角a的值为135°或315°时,△BCD′与△DCD′全等.
20.(1)见解析
(2)点的坐标为,点的坐标为
【分析】(1)将点、点的坐标分别绕点按逆时针方向旋转,得到对应点、,顺次连接各点即可得到;
(2)根据图形直接写出点、的坐标即可.
【详解】(1)解:将点、点的坐标分别绕点按逆时针方向旋转,得到对应点、,顺次连接各点即可得到,如图所示:
;
(2)解:由图可知:
点的坐标为,点的坐标为.
【点睛】本题主要考查了旋转的性质、坐标与图形,根据题意画出旋转后的图形是解题的关键.
21.(1)等边;(2)存在,△BDE的周长最小值为:2+4
【分析】(1)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;
(2)当6<m<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;
【详解】解:(1)证明:由旋转性质,得:∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
故答案为:等边;
(2)存在,当6<m<10时,
由旋转的性质得,BE=AD,
∴C△DBE=BE+DB+DE
=AB+DE
=4+DE,
由(1)知,△CDE是等边三角形,
∴DE=CD,
∴C△DBE=CD+4,
由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,
此时,AD=2,
∴CD=,
∴△BDE的周长最小值为:2+4.
【点睛】本题考查了几何变换的综合题,旋转的性质,等边三角形的判定和性质,三角形周长的计算,熟练掌握旋转的性质是解题的关键.
22.(1)旋转中心为点A,旋转的度数为
(2),
【分析】(1)根据图形可得旋转中心为点A,根据三角形的内角和定理求出,结合旋转的性质即可得出旋转角的度数;
(2)
【详解】(1)解:,
即,
所以旋转中心为点A,旋转的度数为;
(2)解:逆时针旋转一定角度后与重合,
,,,
,
∵点C恰好成为的中点,
,
.
【点睛】本题主要考查了旋转的性质,解题的关键是掌握旋转前后对应边相等,对应角相等,对应边连线的夹角等于旋转角.
23.(1)①B(2,0);②A(-1,2);
(2)①E′(3+a,3+a);②FF′的最小值为3.
【分析】(1)①②根据“垂直图形”的定义解决问题即可;
(2)①构造全等三角形,利用全等三角形的性质求解即可;
②△FGF′是等腰直角三角形,当FG⊥x轴时,FG取得最小值,即FF′有最小值,据此求解即可解决问题.
【详解】(1)解:①如图中,观察图象可知B(2,0);
②如图,
∵∠AOB=∠ACO=∠ODB=90°,
∴∠A+∠AOC=90°,∠AOC+∠BOD=90°,
∴∠A=∠BOD,
∵AO=OB,
∴△AOC≌△OBD(AAS),
∴OC=BD=1,AC=OD=2,
∴A(-1,2);
(2)解:①如图,过点E作EP⊥x轴于P,过点E′作E′H⊥x轴于H.
∵∠EPG=∠EGE′=∠GHE′=90°,
∴∠E+∠PGE=90°,∠PGE+∠E′GH=90°,
∴∠E=∠E′GH,
∵EG=GE′,
∴△EPG≌△GHE′(AAS),
∴EP=GH=3,PG=E′H=a+3,
∴OH=3+a,
∴E′(3+a,3+a);
②∵∠FGF′=90°,FG=GF′,
∴△FGF′是等腰直角三角形,
∴FF′=FG,
当FG⊥x轴时,FG取得最小值,即FF′有最小值,
∴FF′的最小值为3.
【点睛】本题考查几何变换综合题,考查了旋转变换,全等三角形的判定和性质,等腰直角三角形的判定和性质,勾股定理等知识,解题的关键是理解题意,学会添加常用辅助线,构造全等三角形解决问题.
24.(1)见解析;(2)见解析;(3)见解析;(4)见解析;(5)见解析;(6)见解析.
【分析】(1)把所有的点左平移3个单位长度即可;
(2)把所有的点向下平移4个单位长度即可;
(3)把所有的点向左平移3个单位长度,再向下平移4个单位长度即可;
(4)画出所有的点关于x轴的对称点即可;
(5)画出所有的点关于y轴的对称点即可;
(6)画出所有的点关于原点的对称点即可.
【详解】解:(1)将图案N向左平移3个单位长度,平移后的图案如图1所示:
(2)将图案N向下平移4个单位长度,平移后的图案如图2所示:
(3)将图案N先向左平移3个单位长度,再向下平移4个单位长度,第二次平移后的图案如图3所示:
(4)图案N关于横轴对称的图案如图4所示:
(5)图案N关于纵轴对称的图案如图5所示:
(6)以原点为对称中心,与图案N成中心对称的图案如图6所示:
【点睛】本题考查利用平移、旋转、轴对称设计图案,解题的关键是理解平移、旋转、轴对称的性质,属于中考作图题目中常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.1图形的旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,三角形ABC绕点O顺时针旋转后得到三角形,则下列说法中错误的是( )
A. B. C. D.
2.下列图形均可由“基本图案”通过变换得到:(只填序号)
既可以由“基本图案”平移,也可以通过旋转得到的有( )个.
A.1 B.2 C.3 D.4
3.下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是 ( )
A. B.
C. D.
4.如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
A.50° B.60° C.70° D.80°
5.下列四个图形中,形成方法与另外三个不同的是( ).
A. B. C. D.
6.如图,直线:交轴于,交轴于,轴上一点,为轴上一动点,把线段绕点逆时针旋转得到线段,连接,,则当长度最小时,线段的长为( )
A. B. C.5 D.
7.在下图右侧的四个三角形中,不能由左侧的三角形经过旋转或平移得到的是( )
A.A B.B C.C D.D
8.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是( )
A.2 B.3 C.5 D.6
9.在中,,点D为中点,,绕点D旋转,分别与边交于E,F两点.下列结论:①;②;③;④始终为等腰直角三角形,其中正确的个数有( ).
A.1个 B.2个 C.3个 D.4个
10.如图,在的正方形网格中,由旋转得到,其旋转中心是( )
A.点 B.点 C.点 D.点
11.一个图形经过旋转变换,下列说法中:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有改变.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
12.如图,将三角形ABC绕着点C顺时针旋转60°后得到三角形A′B′C,若∠A=40°,∠B=110°,则∠A′CB′的度数是( )
A. B. C. D.
二、填空题
13.如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为 .
14.等边绕其外心旋转,至少要旋转 度才能与原图形重合.
15.有如图,从图形甲到图形乙,所进行的图形运动是先绕点 时针旋转,再向右移动 格.
16.在正方形、长方形、线段、等边三角形和平行四边形这五种图形中,是旋转对称图形不是中心对称图形的是 .
17.正九边形绕它的旋转中心至少旋转 °后才能与原图形重合.
三、解答题
18.如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O,按逆时针方向旋转30°到 ,那么点的位置可以用(2,30°)表示.如果将再沿逆时针方向继续旋转45°,到,那么点的位置可以用( , )表示.
19.如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至,旋转角为.
(1)当点′恰好落在EF边上时,求旋转角的值;
(2)如图2,G为BC的中点,且0°<<90°,求证:;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.
20.如图,点、的坐标分别为、.将绕点按逆时针方向旋转得到.
(1)画出:
(2)写出点、的坐标.
21.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.
(1)问题发现
如图1,△CDE的形状是______三角形.
(2)探究证明
如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
22.如图,中,,,,逆时针旋转一定角度后与重合,且点C恰好成为的中点.
(1)指出能转中心,并求出旋转的度数;
(2)求出的度数和的长.
23.定义:将图形M绕点P顺时针旋转90°得到图形N,则图形N称为图形M关于点P的“垂直图形”.例如:在下图中,点D为点C关于点P的“垂直图形”.
(1)点A关于原点O的“垂直图形”为点B.
①若点A的坐标为(0,2),直接写出点B的坐标;
②若点B的坐标为(2,1),直接写出点A的坐标;
(2)E(-3,3),F(-2,3),G(a,0).线段EF关于点G的“垂直图形”记为E′F′,点E的对应点为E′,点F的对应点为F′.
①求点E′的坐标;
②当点G运动时,求的最小值.
24.在平面直角坐标系中,将坐标为的点用线段依次连接起来得到一个图案N.
(1)将图案N向左平移3个单位长度,画出平移后的图案;
(2)将图案N向下平移4个单位长度,画出平移后的图案;
(3)将图案N先向左平移3个单位长度,再向下平移4个单位长度,画出第二次平移后的图案;
(4)画出图案N关于横轴对称的图案;
(5)画出图案N关于纵轴对称的图案;
(6)以原点为对称中心,画出与图案N成中心对称的图案.
《9.1图形的旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B B B B D D A
题号 11 12
答案 C B
1.A
【分析】根据点O没有条件限定,不一定在AB的垂直平分线上,可判断A,根据性质性质可判断B、C、D.
【详解】解:A.当点O在AB的垂直平分线上时,满足OA=OB,由点O没有限制条件,为此点O为任意的,不一定在AB的垂直平分线上,故选项A不正确,符合题意;
B.由旋转可知OC与OC′是对应线段,由旋转性质可得OC=OC′,故选项B正确,不符合题意;
C.因为、都是旋转角,由旋转性质可得,故选项C正确,不符合题意;
D.由旋转可知与是对应角,由性质性质可得,故选项D正确,不符合题意.
故选择A.
【点睛】本题考查线段垂直平分线性质,图形旋转及其性质,掌握线段垂直平分线性质,图形旋转及其性质是解题关键.
2.A
【分析】此题是一组复合图形,根据平移、旋转的性质解答.
【详解】解:①可以看作由左边图案向右平移得到的;
②可以看作一个菱形绕一个顶点旋转得到的;
③既可以看作一个圆向右平移得到的,也可以看作两个圆组成的图案旋转得到的;
④可以看作上面基本图案向下平移得到的;
⑤可以看作上面图案绕中心旋转得到的.
故可以平移但不能旋转的是①④;
可以旋转但不能平移的是②⑤;
既可以平移,也可以旋转的是③.
故答案为A.
【点睛】本题考查平移、旋转的性质:①平移不改变图形的形状和大小;经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.②旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心,熟练掌握其性质是解决此题的关键.
3.D
【分析】寻找基本图形,旋转中心,旋转角,旋转次数,逐一判断.
【详解】A.可由一个基本花瓣绕其中心经过7次旋转,每次旋转45度得到;
B. 可由一个基本菱形绕其中心经过5次旋转,每次旋转 60度得到;
C. 可由一个基本花瓣绕其中心旋转180度得到;
D. 不能由基本图案旋转得到;
故选D.
【点睛】此题主要考查旋转设计图案.
4.B
【详解】∵在三角形ABC中,∠ACB=90°,∠B=50°,
∴∠A=180°﹣∠ACB﹣∠B=40°.
由旋转的性质可知:BC=B′C,∠OB′C=∠B
∴∠B=∠BB′C=50°.
又∵∠BB′C=∠A+∠ACB′=40°+∠ACB′,
∴∠ACB′=10°,
∴∠COA′=∠AOB′=∠OB′C+∠ACB′=∠B+∠ACB′=60°.
故选B.
【点睛】考点:旋转的性质.
5.B
【分析】本题考查的是旋转与轴对称的性质,利用旋转或轴对称逐一分析各选项即可.
【详解】解:A,C,D选项中的图形都是通过将其中一部分旋转形成的图形,而B选项中的图形是通过轴对称形成的,
故答案为:B
6.B
【分析】作EH⊥x轴于H,通过证明△DBO≌△BEH,可得HE=OB,从而确定点点的运动轨迹是直线,根据垂线段最短确定出点E的位置,然后根据勾股定理求解即可.
【详解】解:作EH⊥x轴于H,
∵∠DBE=90°,
∴∠DBC+∠CBE=90°.
∵∠BHE=90°,
∴∠BEH+∠CBE=90°,
∴∠DBC=∠BEH.
在△DBO和△BEH中,
∵∠DBC=∠BEH,
∠BOD=∠BHE,
BD=BE,
∴△DBO≌△BEH中,
∴HE=OB,
当y=0时,,
∴x=3,
∴HE=OB=3,
∴点的运动轨迹是直线,B(3,0),
∴当⊥m时,CE最短,此时点的坐标为(-1,3),
∵B(-1,0),B(3,0),
∴BC=4,
∴BE′=,
∴BD= BE′=4,
∴OD=,
∴CD=.
故选B.
【点睛】本题考查一次函数与坐标轴的交点,坐标与图形的变化,旋转变换、全等三角形的判定与性质,垂线段最短以及勾股定理等知识,解题的关键是确定点E的位置.
7.B
【详解】试题解析:A、可由△ABC逆时针旋转一个角度得到;
B、可由△ABC翻折得到;
C、可由△ABC逆时针旋转一个角度得到;
D、可由△ABC逆时针旋转一个角度得到.
故选B.
点睛:旋转的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点为旋转中心;②旋转方向;③旋转角度.
8.D
【分析】根据∠A+∠APO=∠POD+∠COD,可得∠APO=∠COD,进而可以证明△APO△COD,进而可以证明AP=CO,即可解题.
【详解】解:∵∠A+∠APO=∠POD+∠COD,∠A=∠POD,
∴∠APO=∠COD,
在△APO和△COD中 ,
∴△APO△COD(AAS),
即AP=CO,
∵CO=AC-AO=6,
∴AP=6.
故答案为6.
【点睛】本题是全等三角形与旋转的综合题型,理解题意,找出全等的三角形,再通过代换求得答案是解题的关键.
9.D
【分析】本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,三角形的面积公式的运用,连接,根据等腰直角三角形的性质就可以得出,就可以得出,进而得出,就有,由勾股定理就即可求出结论.
【详解】解:连接,
,
点D为中点,,
.,.
,
,
.
在和中,
,
,
,.
,
,
.
,
.
,
,
.
,,
始终为等腰直角三角形.
,
.
,
.
∴正确的有4个.
故选:D.
10.A
【分析】本题主要考查了旋转的性质,熟练掌握旋转中心在对应点连线的垂直平分线上是解题的关键.根据旋转的性质可知:旋转中心在对应点连线的垂直平分线上,进而得出答案.
【详解】 解:根据旋转的性质可知:旋转中心在对应点连线的垂直平分线上, 由图形可知:点在的垂直平分线上,又在的垂直平分线上,
∴旋转中心是点,
故选:A.
11.C
【分析】此题考查了旋转的性质,熟练掌握旋转的性质,根据旋转的性质,逐项进行判断即可.
【详解】解:①一个图形经过旋转变换后,对应线段不一定平行,故此说法错误;
②一个图形经过旋转变换后,对应线段相等,故此说法正确;
③一个图形经过旋转变换后,对应角相等,故此说法正确;
④一个图形经过旋转变换后,图形的形状和大小都没有改变,故此说法正确;
综上分析可知,正确的个数为3个.
故选:C.
12.B
【分析】首先根据旋转的性质可得:∠A′=∠A=40°,∠B′=∠B=110°,然后在△B′CA′中利用三角形的内角和定理求解即可.
【详解】解:由旋转的性质可得:∠A′=∠A=40°,∠B′=∠B=110°,
∴∠A′CB′=180°-∠B′-∠A′=180°-110°-40°=30°.
故选:B.
【点睛】本题主要考查的是旋转的性质、三角形的内角和定理,掌握旋转的性质是解题的关键.
13.
【分析】根据已知及勾股定理求得DP的长,再根据全等三角形的判定得到△B′PH≌△BPD,从而根据直角三角形的性质求得GH,BG的长,从而不难求得旋转前后两个直角三角形重叠部分的面积.
【详解】解:设A′B′交BC于D,B′C′交BC于G、交AB于H,
∵∠C=90°,∠A=60°,
∴∠B=30°,
∴AB=2AC=6 ,
在直角△DPB中,BP=AP=AC=3,
设PD=x,
∵∠A=60°,则∠B=30°,
∴BD=2PD=2x,
∵DP2+BP2=BD2,
∴x2+32=(2x)2,
∴DP=x=,
∵B′P=BP,∠B=∠B′,∠B′PH=∠BPD=90°,
∴△B′PH≌△BPD,
∴PH=PD=,
∵在直角△BGH中,BH=3+,
∴GH=BH=,BG=,
∴S△BGH=××=,S△BDP=×3×=,
∴SDGHP=(cm2).
故答案为:.
【点睛】本题考查了勾股定理,三角形的全等的判定及性质,旋转的性质等知识的综合运用.
14.
【分析】根据三角形外形的定义可得垂直平分,结合等边三角形的性质,推出,等边绕其外心旋转与原图形重合,则点A旋转后应与点C重合,求出即可.
【详解】解:如图,点O为的外心,
∴垂直平分,
∵是等边三角形,
∴,平分,
∴,
同理可得的:,
∴,
故答案为:.
【点睛】本题主要考查了等边三角形的性质,旋转的性质,外形的定义,解题的关键是掌握三角形的外心是三角形三条垂直平分线的交点.
15. 逆 10
【分析】根据旋转性质及平移性质即可得到答案.
【详解】解:观察甲乙两图可知,将甲图以为旋转中心,逆时针旋转,再向右平移个单位长度即可得到乙图,
故答案为:逆;.
【点睛】本题考查旋转及平移性质,熟记旋转性质及平移性质作图是解决问题的关键.
16.等边三角形
【分析】根据中心对称图形的定义以及旋转图形的性质分别判断得出即可.
【详解】正方形、长方形、线段、等边三角形和平行四边形这五种图形中、线段和平行四边形和正方形和长方形都是中心对称图形,只有等边三角形是旋转对称图形但不是中心对称图形;故答案为:等边三角形.
【点睛】此题主要考查了旋转图形的性质,注意中心对称图形也属于旋转图形,但要按要求答题
17.40.
【分析】要与原来的九边形重合.可用一个圆周角的度数(即360度)除以9,便可知道至少要旋转多少度才能和原来的五边形重合.
【详解】∵=40°,
故答案为:40.
18.(2,75°)
【分析】根据旋转的性质,旋转不改变图形的大小和形状,即旋转后所得图形与原图形全等,通过分析坐标的形成即可解答.
【详解】解:第一个坐标为原点到此点的距离,旋转前后线段长度不变,所以OA″=OA=2,
第二个坐标为与x轴的夹角=∠A″OA′+∠A′OA=45°+30°=75°,
那么点A”的位置可以用( 2,75°)表示,
故答案为(2,75°).
19.(1)∠α=30°(2)见解析(3)旋转角a的值为135°或315°时,△BCD′与∠DCD′全等
【分析】(1)根据旋转的性质得CE=CH=1,即可得出结论;
(2)由G为BC中点可得CG=CE,根据旋转的性质得∠D′CE′=∠DCE=90°,CE=CE′CE,则∠GCD′=∠DCE′=90°+α,然后根据“SAS”可判断△GCD′≌△E′CD,则GD′=E′D;
(3)根据正方形的性质得CB=CD,而CD=CD′,则△BCD′与△DCD′为腰相等的两等腰三角形,当两顶角相等时它们全等,当△BCD′与△DCD′为钝角三角形时,可计算出α=135°,当△BCD′与△DCD′为锐角三角形时,可计算得到α=315°.
【详解】解:(1)∵长方形CEFD绕点C顺时针旋转至CE′F′D′,
∴CE=CH=1,
∴△CEH为等腰直角三角形,
∴∠ECH=45°,
∴∠α=30°;
(2)证明:∵G为BC中点
∴CG=1
∴CG=CE
∵长方形CEFD绕点C顺时针旋转至CE′F′D′
∴∠D′CE′=∠DCE=90°,CE=CE′=CG
∴∠GCD′=∠DCE′=90°+α
在△GCD′和△E′CD中
∵CD′=CD,∠GCD=∠DCE′,CG=CE′
∴△GCD′≌△E′CD(SAS)
∴GD′=E′D;
(3)解:能.
理由如下:
∵四边形ABCD为正方形
∴CB=CD
∵CD′=CD′
∴△BCD′与△DCD′为腰相等的两等腰三角形,当∠BCD′=∠DCD′时,△BCD′≌△DCD′,当△BCD′与△DCD′为钝角三角形时,则旋转角α=(360°-90°)÷2=135°
当△BCD′与△DCD′为锐角三角形时,∠BCD′=∠DCD′=∠BCD=45°,则α=360°﹣90°÷2=315°
即旋转角a的值为135°或315°时,△BCD′与△DCD′全等.
20.(1)见解析
(2)点的坐标为,点的坐标为
【分析】(1)将点、点的坐标分别绕点按逆时针方向旋转,得到对应点、,顺次连接各点即可得到;
(2)根据图形直接写出点、的坐标即可.
【详解】(1)解:将点、点的坐标分别绕点按逆时针方向旋转,得到对应点、,顺次连接各点即可得到,如图所示:
;
(2)解:由图可知:
点的坐标为,点的坐标为.
【点睛】本题主要考查了旋转的性质、坐标与图形,根据题意画出旋转后的图形是解题的关键.
21.(1)等边;(2)存在,△BDE的周长最小值为:2+4
【分析】(1)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;
(2)当6<m<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;
【详解】解:(1)证明:由旋转性质,得:∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
故答案为:等边;
(2)存在,当6<m<10时,
由旋转的性质得,BE=AD,
∴C△DBE=BE+DB+DE
=AB+DE
=4+DE,
由(1)知,△CDE是等边三角形,
∴DE=CD,
∴C△DBE=CD+4,
由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,
此时,AD=2,
∴CD=,
∴△BDE的周长最小值为:2+4.
【点睛】本题考查了几何变换的综合题,旋转的性质,等边三角形的判定和性质,三角形周长的计算,熟练掌握旋转的性质是解题的关键.
22.(1)旋转中心为点A,旋转的度数为
(2),
【分析】(1)根据图形可得旋转中心为点A,根据三角形的内角和定理求出,结合旋转的性质即可得出旋转角的度数;
(2)
【详解】(1)解:,
即,
所以旋转中心为点A,旋转的度数为;
(2)解:逆时针旋转一定角度后与重合,
,,,
,
∵点C恰好成为的中点,
,
.
【点睛】本题主要考查了旋转的性质,解题的关键是掌握旋转前后对应边相等,对应角相等,对应边连线的夹角等于旋转角.
23.(1)①B(2,0);②A(-1,2);
(2)①E′(3+a,3+a);②FF′的最小值为3.
【分析】(1)①②根据“垂直图形”的定义解决问题即可;
(2)①构造全等三角形,利用全等三角形的性质求解即可;
②△FGF′是等腰直角三角形,当FG⊥x轴时,FG取得最小值,即FF′有最小值,据此求解即可解决问题.
【详解】(1)解:①如图中,观察图象可知B(2,0);
②如图,
∵∠AOB=∠ACO=∠ODB=90°,
∴∠A+∠AOC=90°,∠AOC+∠BOD=90°,
∴∠A=∠BOD,
∵AO=OB,
∴△AOC≌△OBD(AAS),
∴OC=BD=1,AC=OD=2,
∴A(-1,2);
(2)解:①如图,过点E作EP⊥x轴于P,过点E′作E′H⊥x轴于H.
∵∠EPG=∠EGE′=∠GHE′=90°,
∴∠E+∠PGE=90°,∠PGE+∠E′GH=90°,
∴∠E=∠E′GH,
∵EG=GE′,
∴△EPG≌△GHE′(AAS),
∴EP=GH=3,PG=E′H=a+3,
∴OH=3+a,
∴E′(3+a,3+a);
②∵∠FGF′=90°,FG=GF′,
∴△FGF′是等腰直角三角形,
∴FF′=FG,
当FG⊥x轴时,FG取得最小值,即FF′有最小值,
∴FF′的最小值为3.
【点睛】本题考查几何变换综合题,考查了旋转变换,全等三角形的判定和性质,等腰直角三角形的判定和性质,勾股定理等知识,解题的关键是理解题意,学会添加常用辅助线,构造全等三角形解决问题.
24.(1)见解析;(2)见解析;(3)见解析;(4)见解析;(5)见解析;(6)见解析.
【分析】(1)把所有的点左平移3个单位长度即可;
(2)把所有的点向下平移4个单位长度即可;
(3)把所有的点向左平移3个单位长度,再向下平移4个单位长度即可;
(4)画出所有的点关于x轴的对称点即可;
(5)画出所有的点关于y轴的对称点即可;
(6)画出所有的点关于原点的对称点即可.
【详解】解:(1)将图案N向左平移3个单位长度,平移后的图案如图1所示:
(2)将图案N向下平移4个单位长度,平移后的图案如图2所示:
(3)将图案N先向左平移3个单位长度,再向下平移4个单位长度,第二次平移后的图案如图3所示:
(4)图案N关于横轴对称的图案如图4所示:
(5)图案N关于纵轴对称的图案如图5所示:
(6)以原点为对称中心,与图案N成中心对称的图案如图6所示:
【点睛】本题考查利用平移、旋转、轴对称设计图案,解题的关键是理解平移、旋转、轴对称的性质,属于中考作图题目中常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
