7.3频数和频率同步强化练习(含解析)
文档属性
| 名称 | 7.3频数和频率同步强化练习(含解析) | 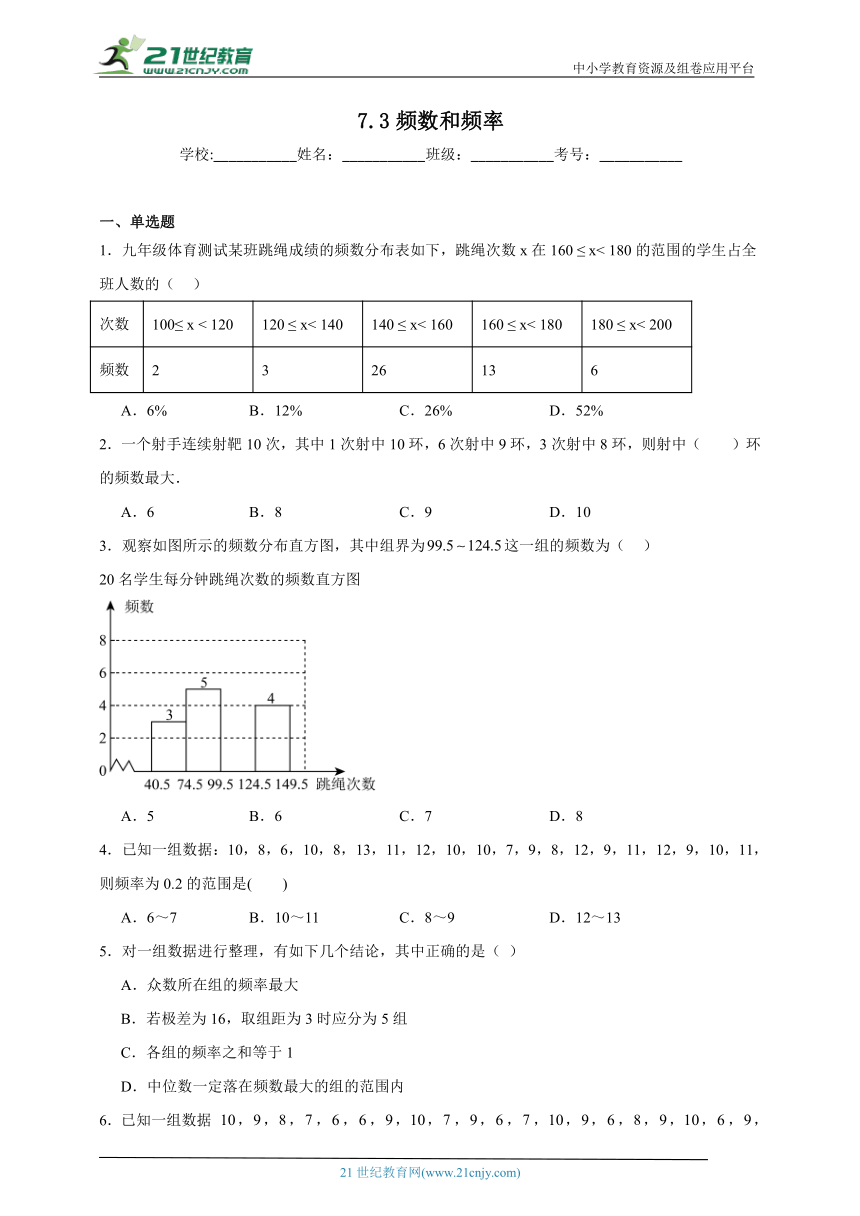 | |
| 格式 | docx | ||
| 文件大小 | 682.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 13:36:17 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
7.3频数和频率
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.九年级体育测试某班跳绳成绩的频数分布表如下,跳绳次数x在160 ≤ x< 180的范围的学生占全班人数的( )
次数 100≤ x < 120 120 ≤ x< 140 140 ≤ x< 160 160 ≤ x< 180 180 ≤ x< 200
频数 2 3 26 13 6
A.6% B.12% C.26% D.52%
2.一个射手连续射靶10次,其中1次射中10环,6次射中9环,3次射中8环,则射中( )环的频数最大.
A.6 B.8 C.9 D.10
3.观察如图所示的频数分布直方图,其中组界为这一组的频数为( )
20名学生每分钟跳绳次数的频数直方图
A.5 B.6 C.7 D.8
4.已知一组数据:10,8,6,10,8,13,11,12,10,10,7,9,8,12,9,11,12,9,10,11,则频率为0.2的范围是( )
A.6~7 B.10~11 C.8~9 D.12~13
5.对一组数据进行整理,有如下几个结论,其中正确的是( )
A.众数所在组的频率最大
B.若极差为16,取组距为3时应分为5组
C.各组的频率之和等于1
D.中位数一定落在频数最大的组的范围内
6.已知一组数据 ,,,,,,,,,,,,,,,,,,,,那么频率为 的范围是 ( )
A. B. C. D.
7.下列说法中,正确的是( )
A.频数表示每个对象出现的次数与总次数的比值
B.频率表示每个对象出现的次数
C.频数与总次数的比值是频率
D.频率与总次数的比值是频数
8.已知样本:7,12,11,10,13,8,7,14,9,10,8,11,10,8,10,9,12,9,13,11,这组数据中在范围8.5~11.5内的频数应该是( )
A.8 B.9 C.10 D.11
9.在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球实验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )
A.2个 B.4个 C.18个 D.16个
10.随机抽查了某校七年级63名学生的身高(单位:cm),所得到的数据中最大值是172,最小值是149、若取组距为4,则这些数据可分成( )组.
A.5 B.6 C.7 D.8
11.为推广全民健身运动,某单位组织员工进行爬山比赛,在50名报名者中,青年组有17人,中年组有20人,老年组有13人,则青年组的频率是( )
A.0.34 B.0.4 C.0.26 D.0.6
12.抛20次硬币,出现“反面朝上”的频率为,则出现“正面朝上”的次数为( )
A.9 B.10 C.11 D.12
二、填空题
13.在纸上写下一组数字“20240628”, 这组数字中8出现的频数是
14.某同学统计了他上周通话次数及每次的通话时间,并列出频数分布表:
通话时间x(分钟)
通话次数(频数) 26 14 7 2 1
则通话时间超过6分钟的频率是 .
15.已知某组数据的频数为49,频率为0.7,则样本容量为
16.小明抛掷一枚硬币40次,正面朝上的频率是0.40,则正面朝下的频数是 .
17.对某班40位同学的一次考试成绩进行统计,若频数分布表中80.5~90.5分这一组的频率是0.2,则成绩在该分数段的人数是 .
三、解答题
18.小华统计了他家1月份打电话的次数及通话时间,并列出频数分数布表:
通话时间 频数(通话次数)
24
16
8
10
16
(1)小华家1月份一共打了多少次电话?
(2)求通话时间不超过15的频率.
19.小明对本校八年级530名学生的体育达标情况进行调查,按A,B,C三等成绩进行统计并制作出如图所示的统计图,其中,(1)班有50人,A等成绩为40以上,B等成绩为(不含40),C等为不达标,成绩为(不含30).根据图中信息解答下面问题:
(1)若除1班外,其余班级学生体育考试成绩在B等的有120人,请补全扇形统计图.
(2)若要求全年级学生的体育达标率不低于90%,在本次调查中,该年级全体学生的体育达标率是否符合要求?如果不符合要求,还需要增加几个同学的成绩达标?
20.掷一枚正方体的骰子,各个面上分别标有数字1,2,3,4,5,6,求下列事件发生的频率的大小:
①朝上的数字是奇数;
②朝上的数字能被3除余1;
③朝上的数字小于6;
④朝上的数字不小于3.
21.为了改进银行的服务质量,随机抽随机抽查了名顾客,统计了顾客在窗口办理业务所用的时间(单位:分钟)下图是这次调查得到的统计图.
请你根据图中的信息回答下列问题:
(1)求办理业务所用的时间为分钟的人教;
(2)补全条形统计图;
(2)求这名顾客办理业务所用时间的平均数.
22.在某项针对~岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为,规定:当时为级,当时为级,当时为级.现随机抽取个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下:
求样本数据中为A级的频率.
23.某班“红心义卖”活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
转动转盘的次数n 100 200 300 400 500 600
落在“书画作品”区域的次数m 60 122 180 232 a 604
落在“书画作品”区域的频率m/n 0.6 0.61 0.6 b 0.59 0.604
(1)完成上述表格:a=____,b=_____;
(2)当n很大时,频率将会接近一个稳定的数值.假如你去转动该转盘一次,你获得“书画作品”的概率约是__;(结果精确到0.1)
(3)如果要使获得“手工作品”的可能性大于获得“书画作品”的可能性,则表示“手工作品”扇形区域的圆心角还要增加多少度以上?
24.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵
《7.3频数和频率》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D D C D C C D B
题号 11 12
答案 A C
1.C
【分析】根据频数与频率的计算公式,即可得解.
【详解】根据题意,得跳绳次数在160 ≤< 180的范围的学生占全班人数的百分比为
故选:C.
【点睛】此题主要考查了读频数分布表获取信息的能力.必须认真观察、分析、研究,才能作出正确的判断和解决问题.
2.C
【详解】解:根据题意,可6次射中9环,次数最多;故射中9环的频数最大.故选C.
3.D
【分析】用总人数减去其他三组的人数即为所求频数.
【详解】解:由题意得:,
∴组界为这一组的频数为8,
故选:D.
【点睛】本题考查频数分布直方图,能够根据要求读出相应的数据是解决本题的关键.
4.D
【分析】分别计算出各组的频数,再除以20即可求得各组的频率,看谁的频率等于0.2.
【详解】A中,其频率=2÷20=0.1;
B中,其频率=8÷20=0.4;
C中,其频率=6÷20=0.3;
D中,其频率=4÷20=0.2.
故选D.
【点睛】首先数出数据的总数,然后数出各个小组内的数据个数,即频数.根据频率=频数÷总数进行计算.
5.C
【详解】试题分析:根据统计的相关知识依次分析各项即可.
A.众数所在组的频率不一定最大,故本选项错误;
B.若极差为16,取组距为3时应分为6组,故本选项错误;
C.各组的频率之和等于1,本选项正确;
D.中位数是大小排列后最中间的数,不一定落在频数最大的组的范围内,故本选项错误;
故选C.
考点:本题考查的是统计的知识
点评:解答本题的关键是熟练掌握各小组频数之和等于数据总和,各小组频率之和等于1.
6.D
【详解】试题解析:对于选项A,5.5-7.5的频数为8,频率=8÷20=0.4<0.5,故A选项错误;
对于B选项,6.5-8.5的频数为5,频率=5÷20=0.25<0.5,故B选项错误;
对于C选项,7.5-9.5的频数为8,频率=8÷20=0.4<0.5,故C选项错误;
对于D选项,8.5-10.5的频数为10,频率=10÷20=0.5,故D选项正确,
故选D.
7.C
【分析】本题考查了频率与频数的概念,解题的关键是熟练的掌握频率与频数的概念.
根据频率与频数的概念求解即可.
【详解】A.频数是表示一组数据中,符合条件的对象出现的次数,故错误;
B.频率是表示一组数据中,符合条件的对象出现的次数和总次数的比值,故错误;
C.频数与总次数的比值是频率,符合频率的意义,故正确;
D.频率与总次数的乘积是频数,故错误.
故选C.
8.C
【分析】频数是指符合要求的对象出现的次数,从而仔细查找数据中在8.5~11.5范围内的数据的数量即可得出答案.
【详解】样本中在范围8.5~11.5中的数据有:11、10、9、10、11、10、10、9、9、11,共10个,即这级样本数据落在范围8.5~11.5的频数是10.
故选C.
【点睛】本题考查频数的概念,比较基础,解答本题的关键是掌握频数是指符合要求的对象出现的次数.
9.D
【分析】根据频率=频数÷总数,可以求得白色乒乓球的个数,从而得到黄色乒乓球个数.
【详解】解:∵白色乒乓球的频率稳定在0.2左右
∴白色乒乓球的个数=20×0.2=4个
∴黄色乒乓球的个数=20-4=16个
故选D.
【点睛】本题主要考查了频率与频数的计算,解题的关键在于能够熟练掌握频率=频数÷总数.
10.B
【详解】解:(172﹣149)÷4=23÷4≈6组.故选B.
点睛:此题考查的是组数的确定方法,组数=极差÷组距.
11.A
【分析】本题考查频数与频率,用青年组的人数除以总人数可得青年组的频率.
【详解】解:青年组的频率是,
故选A.
12.C
【分析】本题考查了频数与频率,熟练掌握频数总次数频率是解题的关键.
根据频数总次数频率,进行计算即可解答.
【详解】解:由题意得:,
故选:C.
13.1
【分析】本题考查了频数的定义,根据出现的次数为频数,即可求解.
【详解】解:“20240628”这组数字中8出现的频数为1,
故答案为:1.
14.
【分析】本题主要掌握观察频数分布表,考查了频率计算公式,频率等于频数与数据总数的比.根据频率计算公式,频率等于频数与数据总数的比即可求解.
【详解】解:通话时间超过6分钟的频率为:
故答案为:
15.70
【分析】根据即可求解.
【详解】解:样本容量为,
故答案为:70.
【点睛】本题考查频数与频率,掌握是解题的关键.
16.24
【分析】本题考查了根据数据描述求频数,运用频数=总数乘频率进行列式计算得正面朝上的频数是,即可求出正面朝下的频数,进行作答即可.
【详解】解:∵小明抛掷一枚硬币40次,正面朝上的频率是0.40,
∴正面朝上的频数是,
∴正面朝下的频数是,
故答案为:24.
17.8
【分析】本题考查频数的求法,因为人数个数就是频数,频数总数频率,从而可求出解.
【详解】解:∵,
∴这个分数段的人数是8.
故答案为:8.
18.(1)74次
(2)
【分析】(1)根据表格将通话次数相加即可;
(2)利用频率的计算公式进行计算即可.
【详解】(1)解:(次);
答:小华家1月份一共打了74次电话.
(2)解:通话时间不超过15的次数为:,
∴;
∴通话时间不超过15的频率为:.
【点睛】本题考查频率的计算,熟练掌握频率的计算公式是解题的关键.
19.(1)见解析
(2)不符合要求,需增加12人
【分析】(1)先求出其余各班的人数,再求出其所占的百分比,最后求出其圆心角度数即可;
(2)分别计算1班和其它班的达标率,得出1班达标率符合要求,其他班达标率不符合要求,再进行计算即可.
【详解】(1)解:其余各班的人数为(人),
B等成绩人数所占的百分比:
A等成绩人数所占的百分比∶
B等成绩人数所占的角度为,
补全扇形统计图∶
;
(2)解:1班达标率为,
其余各班学生体育达标率为,
所以,年级全体学生的体育达标率不符合要求,
需要达标增加的人数(人).
【点睛】本题主要考查了频率分布直方图,以及求扇形统计图中是数据,解题的关键是正确理解题意,根据题中和图中的信息求出需要数据.
20.①;②;③;④.
【分析】根据频率的计算公式,逐一计算各个小题,即可.
【详解】①一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,是奇数点的有3种可能,故其频率是;
②一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,掷出朝上的数字能被3除余1的有1,4,故发生的频率为;
③一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,朝上的数字小于6的有1, 2,3,4,5,故发生的频率为;
④一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,朝上的数字不小于3的有3,4,5,6,故发生的频率为.
【点睛】本题主要考查频率的计算公式,掌握频率=频数÷总数,是解题的关键.
21.;见解析;
【分析】从条形图中得出每种情况的人数,再计算办理业务所用的时间为11分钟的人数;
根据前面计算的结果补全条形图;
根据平均数的概念求得这30名顾客办理业务所用时间的平均数;
【详解】(1)办理业务所用的时间为11min的人数=30-3-10-7-4-1=5(人)
(2)根据(1)补全办理业务所用时间为11min的人数是5的条形统计图,如下,
这30名顾客办理业务所用时间的平均数=(8×3+9×10+10×7+11×5+12×4+13×1)÷30=10(min).
【点睛】此题考查频数与频率、条形统计图,解题关键在于看懂图中数据理解题意.
22.
【分析】本题考查了求频率,根据频率等于频数除以总数,即可求解.
【详解】解:的人数为,
故样本数据中为级的频率为
23.(1)295、0.58;(2)0.6;(3)36゜
【分析】(1)利用频率乘以次数得到a的值,利用m除以n即可求出b的值;
(2)根据表格中的数据可以估计频率是多少以及转动该转盘一次,获得“书画作品”的概率;
(3)根据扇形统计图和表格中的数据可以估计表示“手工作品”区域的扇形的圆心角至少还要增加的度数.
【详解】解:(1)由题意可得:a=500×0.59=295,b=232÷400=0.58,
故答案为:295,0.58;
(2)由表格中的数据可得,当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“书画作品”的概率约是0.6,
故答案为:0.6;
(3)由题意可得,要使获得“手工作品”的可能性大于获得“书画作品”的可能性,则表示“手工作品”区域的扇形的圆心角至少还要增加:360°×0.5-360°×0.4=36°,即要使获得“手工作品”的可能性大于获得“书画作品”的可能性,则表示“手工作品”区域的扇形的圆心角至少还要增加36度.
【点睛】本题考查利用频率估计概率、扇形统计图、可能性大小,解答本题的关键是明确题意,利用数形结合的思想解答本题.
24.(1)0.9附近,0.9;(2)①4.5,15万棵.
【分析】(1)由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9;
(2)①5×成活率即为所求的成活的树苗棵树;
②利用成活率求得需要树苗棵树,减去已移植树苗数即为所求的树苗的棵树.
【详解】(1)0.9 0.9
(2)①4.5
估计该地区已经移植的这种树苗能成活5×0.9=4.5(万棵).
②18÷0.9-5=15(万棵).
答:该地区还需移植这种树苗约15万棵.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.3频数和频率
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.九年级体育测试某班跳绳成绩的频数分布表如下,跳绳次数x在160 ≤ x< 180的范围的学生占全班人数的( )
次数 100≤ x < 120 120 ≤ x< 140 140 ≤ x< 160 160 ≤ x< 180 180 ≤ x< 200
频数 2 3 26 13 6
A.6% B.12% C.26% D.52%
2.一个射手连续射靶10次,其中1次射中10环,6次射中9环,3次射中8环,则射中( )环的频数最大.
A.6 B.8 C.9 D.10
3.观察如图所示的频数分布直方图,其中组界为这一组的频数为( )
20名学生每分钟跳绳次数的频数直方图
A.5 B.6 C.7 D.8
4.已知一组数据:10,8,6,10,8,13,11,12,10,10,7,9,8,12,9,11,12,9,10,11,则频率为0.2的范围是( )
A.6~7 B.10~11 C.8~9 D.12~13
5.对一组数据进行整理,有如下几个结论,其中正确的是( )
A.众数所在组的频率最大
B.若极差为16,取组距为3时应分为5组
C.各组的频率之和等于1
D.中位数一定落在频数最大的组的范围内
6.已知一组数据 ,,,,,,,,,,,,,,,,,,,,那么频率为 的范围是 ( )
A. B. C. D.
7.下列说法中,正确的是( )
A.频数表示每个对象出现的次数与总次数的比值
B.频率表示每个对象出现的次数
C.频数与总次数的比值是频率
D.频率与总次数的比值是频数
8.已知样本:7,12,11,10,13,8,7,14,9,10,8,11,10,8,10,9,12,9,13,11,这组数据中在范围8.5~11.5内的频数应该是( )
A.8 B.9 C.10 D.11
9.在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球实验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )
A.2个 B.4个 C.18个 D.16个
10.随机抽查了某校七年级63名学生的身高(单位:cm),所得到的数据中最大值是172,最小值是149、若取组距为4,则这些数据可分成( )组.
A.5 B.6 C.7 D.8
11.为推广全民健身运动,某单位组织员工进行爬山比赛,在50名报名者中,青年组有17人,中年组有20人,老年组有13人,则青年组的频率是( )
A.0.34 B.0.4 C.0.26 D.0.6
12.抛20次硬币,出现“反面朝上”的频率为,则出现“正面朝上”的次数为( )
A.9 B.10 C.11 D.12
二、填空题
13.在纸上写下一组数字“20240628”, 这组数字中8出现的频数是
14.某同学统计了他上周通话次数及每次的通话时间,并列出频数分布表:
通话时间x(分钟)
通话次数(频数) 26 14 7 2 1
则通话时间超过6分钟的频率是 .
15.已知某组数据的频数为49,频率为0.7,则样本容量为
16.小明抛掷一枚硬币40次,正面朝上的频率是0.40,则正面朝下的频数是 .
17.对某班40位同学的一次考试成绩进行统计,若频数分布表中80.5~90.5分这一组的频率是0.2,则成绩在该分数段的人数是 .
三、解答题
18.小华统计了他家1月份打电话的次数及通话时间,并列出频数分数布表:
通话时间 频数(通话次数)
24
16
8
10
16
(1)小华家1月份一共打了多少次电话?
(2)求通话时间不超过15的频率.
19.小明对本校八年级530名学生的体育达标情况进行调查,按A,B,C三等成绩进行统计并制作出如图所示的统计图,其中,(1)班有50人,A等成绩为40以上,B等成绩为(不含40),C等为不达标,成绩为(不含30).根据图中信息解答下面问题:
(1)若除1班外,其余班级学生体育考试成绩在B等的有120人,请补全扇形统计图.
(2)若要求全年级学生的体育达标率不低于90%,在本次调查中,该年级全体学生的体育达标率是否符合要求?如果不符合要求,还需要增加几个同学的成绩达标?
20.掷一枚正方体的骰子,各个面上分别标有数字1,2,3,4,5,6,求下列事件发生的频率的大小:
①朝上的数字是奇数;
②朝上的数字能被3除余1;
③朝上的数字小于6;
④朝上的数字不小于3.
21.为了改进银行的服务质量,随机抽随机抽查了名顾客,统计了顾客在窗口办理业务所用的时间(单位:分钟)下图是这次调查得到的统计图.
请你根据图中的信息回答下列问题:
(1)求办理业务所用的时间为分钟的人教;
(2)补全条形统计图;
(2)求这名顾客办理业务所用时间的平均数.
22.在某项针对~岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为,规定:当时为级,当时为级,当时为级.现随机抽取个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下:
求样本数据中为A级的频率.
23.某班“红心义卖”活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
转动转盘的次数n 100 200 300 400 500 600
落在“书画作品”区域的次数m 60 122 180 232 a 604
落在“书画作品”区域的频率m/n 0.6 0.61 0.6 b 0.59 0.604
(1)完成上述表格:a=____,b=_____;
(2)当n很大时,频率将会接近一个稳定的数值.假如你去转动该转盘一次,你获得“书画作品”的概率约是__;(结果精确到0.1)
(3)如果要使获得“手工作品”的可能性大于获得“书画作品”的可能性,则表示“手工作品”扇形区域的圆心角还要增加多少度以上?
24.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵
《7.3频数和频率》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D D C D C C D B
题号 11 12
答案 A C
1.C
【分析】根据频数与频率的计算公式,即可得解.
【详解】根据题意,得跳绳次数在160 ≤< 180的范围的学生占全班人数的百分比为
故选:C.
【点睛】此题主要考查了读频数分布表获取信息的能力.必须认真观察、分析、研究,才能作出正确的判断和解决问题.
2.C
【详解】解:根据题意,可6次射中9环,次数最多;故射中9环的频数最大.故选C.
3.D
【分析】用总人数减去其他三组的人数即为所求频数.
【详解】解:由题意得:,
∴组界为这一组的频数为8,
故选:D.
【点睛】本题考查频数分布直方图,能够根据要求读出相应的数据是解决本题的关键.
4.D
【分析】分别计算出各组的频数,再除以20即可求得各组的频率,看谁的频率等于0.2.
【详解】A中,其频率=2÷20=0.1;
B中,其频率=8÷20=0.4;
C中,其频率=6÷20=0.3;
D中,其频率=4÷20=0.2.
故选D.
【点睛】首先数出数据的总数,然后数出各个小组内的数据个数,即频数.根据频率=频数÷总数进行计算.
5.C
【详解】试题分析:根据统计的相关知识依次分析各项即可.
A.众数所在组的频率不一定最大,故本选项错误;
B.若极差为16,取组距为3时应分为6组,故本选项错误;
C.各组的频率之和等于1,本选项正确;
D.中位数是大小排列后最中间的数,不一定落在频数最大的组的范围内,故本选项错误;
故选C.
考点:本题考查的是统计的知识
点评:解答本题的关键是熟练掌握各小组频数之和等于数据总和,各小组频率之和等于1.
6.D
【详解】试题解析:对于选项A,5.5-7.5的频数为8,频率=8÷20=0.4<0.5,故A选项错误;
对于B选项,6.5-8.5的频数为5,频率=5÷20=0.25<0.5,故B选项错误;
对于C选项,7.5-9.5的频数为8,频率=8÷20=0.4<0.5,故C选项错误;
对于D选项,8.5-10.5的频数为10,频率=10÷20=0.5,故D选项正确,
故选D.
7.C
【分析】本题考查了频率与频数的概念,解题的关键是熟练的掌握频率与频数的概念.
根据频率与频数的概念求解即可.
【详解】A.频数是表示一组数据中,符合条件的对象出现的次数,故错误;
B.频率是表示一组数据中,符合条件的对象出现的次数和总次数的比值,故错误;
C.频数与总次数的比值是频率,符合频率的意义,故正确;
D.频率与总次数的乘积是频数,故错误.
故选C.
8.C
【分析】频数是指符合要求的对象出现的次数,从而仔细查找数据中在8.5~11.5范围内的数据的数量即可得出答案.
【详解】样本中在范围8.5~11.5中的数据有:11、10、9、10、11、10、10、9、9、11,共10个,即这级样本数据落在范围8.5~11.5的频数是10.
故选C.
【点睛】本题考查频数的概念,比较基础,解答本题的关键是掌握频数是指符合要求的对象出现的次数.
9.D
【分析】根据频率=频数÷总数,可以求得白色乒乓球的个数,从而得到黄色乒乓球个数.
【详解】解:∵白色乒乓球的频率稳定在0.2左右
∴白色乒乓球的个数=20×0.2=4个
∴黄色乒乓球的个数=20-4=16个
故选D.
【点睛】本题主要考查了频率与频数的计算,解题的关键在于能够熟练掌握频率=频数÷总数.
10.B
【详解】解:(172﹣149)÷4=23÷4≈6组.故选B.
点睛:此题考查的是组数的确定方法,组数=极差÷组距.
11.A
【分析】本题考查频数与频率,用青年组的人数除以总人数可得青年组的频率.
【详解】解:青年组的频率是,
故选A.
12.C
【分析】本题考查了频数与频率,熟练掌握频数总次数频率是解题的关键.
根据频数总次数频率,进行计算即可解答.
【详解】解:由题意得:,
故选:C.
13.1
【分析】本题考查了频数的定义,根据出现的次数为频数,即可求解.
【详解】解:“20240628”这组数字中8出现的频数为1,
故答案为:1.
14.
【分析】本题主要掌握观察频数分布表,考查了频率计算公式,频率等于频数与数据总数的比.根据频率计算公式,频率等于频数与数据总数的比即可求解.
【详解】解:通话时间超过6分钟的频率为:
故答案为:
15.70
【分析】根据即可求解.
【详解】解:样本容量为,
故答案为:70.
【点睛】本题考查频数与频率,掌握是解题的关键.
16.24
【分析】本题考查了根据数据描述求频数,运用频数=总数乘频率进行列式计算得正面朝上的频数是,即可求出正面朝下的频数,进行作答即可.
【详解】解:∵小明抛掷一枚硬币40次,正面朝上的频率是0.40,
∴正面朝上的频数是,
∴正面朝下的频数是,
故答案为:24.
17.8
【分析】本题考查频数的求法,因为人数个数就是频数,频数总数频率,从而可求出解.
【详解】解:∵,
∴这个分数段的人数是8.
故答案为:8.
18.(1)74次
(2)
【分析】(1)根据表格将通话次数相加即可;
(2)利用频率的计算公式进行计算即可.
【详解】(1)解:(次);
答:小华家1月份一共打了74次电话.
(2)解:通话时间不超过15的次数为:,
∴;
∴通话时间不超过15的频率为:.
【点睛】本题考查频率的计算,熟练掌握频率的计算公式是解题的关键.
19.(1)见解析
(2)不符合要求,需增加12人
【分析】(1)先求出其余各班的人数,再求出其所占的百分比,最后求出其圆心角度数即可;
(2)分别计算1班和其它班的达标率,得出1班达标率符合要求,其他班达标率不符合要求,再进行计算即可.
【详解】(1)解:其余各班的人数为(人),
B等成绩人数所占的百分比:
A等成绩人数所占的百分比∶
B等成绩人数所占的角度为,
补全扇形统计图∶
;
(2)解:1班达标率为,
其余各班学生体育达标率为,
所以,年级全体学生的体育达标率不符合要求,
需要达标增加的人数(人).
【点睛】本题主要考查了频率分布直方图,以及求扇形统计图中是数据,解题的关键是正确理解题意,根据题中和图中的信息求出需要数据.
20.①;②;③;④.
【分析】根据频率的计算公式,逐一计算各个小题,即可.
【详解】①一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,是奇数点的有3种可能,故其频率是;
②一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,掷出朝上的数字能被3除余1的有1,4,故发生的频率为;
③一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,朝上的数字小于6的有1, 2,3,4,5,故发生的频率为;
④一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,朝上的数字不小于3的有3,4,5,6,故发生的频率为.
【点睛】本题主要考查频率的计算公式,掌握频率=频数÷总数,是解题的关键.
21.;见解析;
【分析】从条形图中得出每种情况的人数,再计算办理业务所用的时间为11分钟的人数;
根据前面计算的结果补全条形图;
根据平均数的概念求得这30名顾客办理业务所用时间的平均数;
【详解】(1)办理业务所用的时间为11min的人数=30-3-10-7-4-1=5(人)
(2)根据(1)补全办理业务所用时间为11min的人数是5的条形统计图,如下,
这30名顾客办理业务所用时间的平均数=(8×3+9×10+10×7+11×5+12×4+13×1)÷30=10(min).
【点睛】此题考查频数与频率、条形统计图,解题关键在于看懂图中数据理解题意.
22.
【分析】本题考查了求频率,根据频率等于频数除以总数,即可求解.
【详解】解:的人数为,
故样本数据中为级的频率为
23.(1)295、0.58;(2)0.6;(3)36゜
【分析】(1)利用频率乘以次数得到a的值,利用m除以n即可求出b的值;
(2)根据表格中的数据可以估计频率是多少以及转动该转盘一次,获得“书画作品”的概率;
(3)根据扇形统计图和表格中的数据可以估计表示“手工作品”区域的扇形的圆心角至少还要增加的度数.
【详解】解:(1)由题意可得:a=500×0.59=295,b=232÷400=0.58,
故答案为:295,0.58;
(2)由表格中的数据可得,当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“书画作品”的概率约是0.6,
故答案为:0.6;
(3)由题意可得,要使获得“手工作品”的可能性大于获得“书画作品”的可能性,则表示“手工作品”区域的扇形的圆心角至少还要增加:360°×0.5-360°×0.4=36°,即要使获得“手工作品”的可能性大于获得“书画作品”的可能性,则表示“手工作品”区域的扇形的圆心角至少还要增加36度.
【点睛】本题考查利用频率估计概率、扇形统计图、可能性大小,解答本题的关键是明确题意,利用数形结合的思想解答本题.
24.(1)0.9附近,0.9;(2)①4.5,15万棵.
【分析】(1)由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9;
(2)①5×成活率即为所求的成活的树苗棵树;
②利用成活率求得需要树苗棵树,减去已移植树苗数即为所求的树苗的棵树.
【详解】(1)0.9 0.9
(2)①4.5
估计该地区已经移植的这种树苗能成活5×0.9=4.5(万棵).
②18÷0.9-5=15(万棵).
答:该地区还需移植这种树苗约15万棵.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
