9.5三角形的中位线同步强化练习(含解析)
文档属性
| 名称 | 9.5三角形的中位线同步强化练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 13:35:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
9.5三角形的中位线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
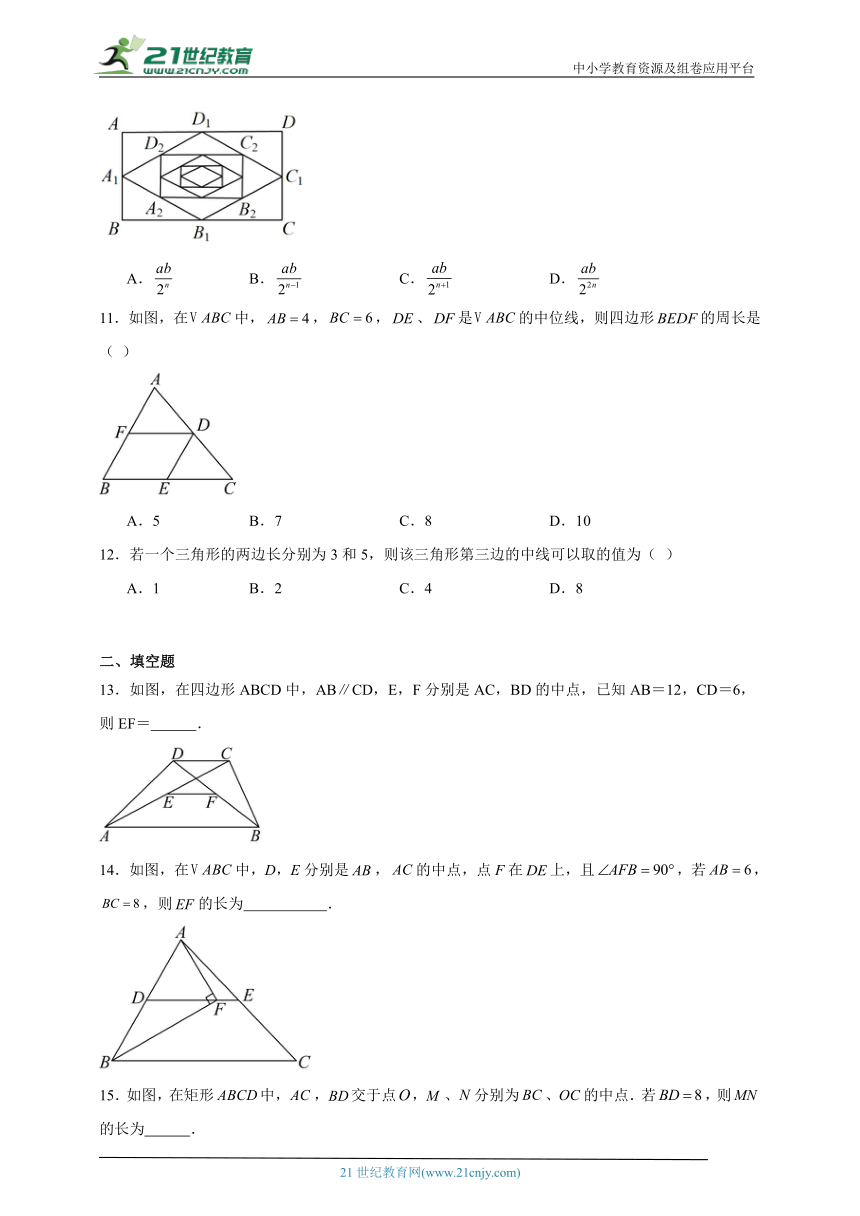
1.如图,在平行四边形中,对角线、相交于点,为的中点,,则的长为( )
A. B. C. D.
2.如图,在平行四边形中,,E为上一动点,M,N分别为,的中点,则的长为( )
A.3 B.4 C.5 D.不确定
3.顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )
A.正方形 B.矩形 C.菱形 D.梯形
4.如果三角形的两边分别为3和5,那么连结这个三角形三边中点所得三角形的周长可能是( )
A.5.5 B.5 C.4.5 D.4
5.如图,中,,,,,,则的值为( )
A.6 B. C.7 D.8
6.如图,在中,,,直角的顶点是的中点,两边,分别交,于点,.现给出以下四个结论:①;②是等腰直角三角形;③;④.当在内绕顶点旋转时(点不与点,重合),上述结论中始终正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
7.如图,点A的坐标为(4,3),AB⊥x轴于点B,点C为坐标平面内一点,OC=2,点D为线段AC的中点,连接BD,则BD的最大值为( )
A.3 B. C. D.
8.三角形三条中位线的长为3、4、5,则此三角形的面积为( )
A.12 B.24 C.36 D.48
9.如图,在中,,点分别为的中点,则( )
A. B.1 C.2 D.4
10.如图,已知矩形ABCD的边长分别为a,b,进行如下操作:第一次,顺次连接矩形ABCD各边的中点,得到四边形;第二次,顺次连接四边形各边的中点,得到四边形;…如此反复操作下去,则第n次操作后,得到四边形的面积是( )
A. B. C. D.
11.如图,在中,,,、是的中位线,则四边形的周长是( )
A.5 B.7 C.8 D.10
12.若一个三角形的两边长分别为3和5,则该三角形第三边的中线可以取的值为( )
A.1 B.2 C.4 D.8
二、填空题
13.如图,在四边形ABCD中,AB∥CD,E,F分别是AC,BD的中点,已知AB=12,CD=6,则EF= .
14.如图,在中,D,E分别是,的中点,点F在上,且,若,,则的长为 .
15.如图,在矩形中,,交于点,、分别为、的中点.若,则的长为 .
16.如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=22m,则AB= m.
17.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为 .
三、解答题
18.在学习完了《18.1平行四边形的性质》之后,王老师在数学活动课上对下面一个问题让学生展开探究活动.
问题情境:图1,在 ABCD中,CA⊥AB,AB=6cm,AC=8cm,点O为AC的中点,动点P在BC边上运动,直线PO交AD于E.
问题发现:数学智慧小组”通过积极的动手操作,观察,猜想,提出了如下问题:
(1)在点P运动的过程中,始终存在PO=OE,为什么?
(2)在点P运动到PO⊥AC时,四边形ABPE是平行四边形,为什么?此时BP的长度是多少?
(3)在点P运动的过程中,四边形ABPE的周长是否存在最小值?如果存在,则四边形ABPE的周长的最小值是 cm;BP的长度为 cm.
问题解决:
“数学智慧小组”欢迎您的加入,请开启您的“问题解决之旅”吧!
19.如图,点是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点、、、依次连接,得到四边形.
(1)求证:四边形是平行四边形;
(2)若为的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
20.如图,是的中位线,点为射线上的一个动点(不与点E重合),作交边于点,连结.
(1)如图1,当点M与点D重合时,求证:四边形是平行四边形;
(2)如图,当四边形是菱形时,,求菱形的面积;
(3)如图3,,在延长线上(可以与点D重合),使得四边形为矩形,求的度数范围.
21.(1)探究:如图(1),点P在线段AB上,在AB的同侧作△APC和△BPD,满足PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G分别是AC、BD、CD边中点,连接EF、FG、EG.求证:∠EFG=∠GEF.
(2)应用:如图(2),点P在线段AB上方,∠APC=∠BPD=90°,图(1)题中的其他条件不变,若EF=2,则四边形ABDC的面积为 .
22.已知:如图,在四边形中,,F,G,E分别是的中点.求证:.
23.如图,在中,,、、分别是、、边上的中点.
.
(1)求证:四边形是菱形;
(2)若,求菱形的周长.
24.如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形中,最多可以有几个平行四边形,证明你的结论.
《9.5三角形的中位线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B A C B B B D A
题号 11 12
答案 D B
1.B
【分析】因为四边形是平行四边形,所以;再根据点是的中点,得出是的中位线,即可解决问题.
【详解】四边形是平行四边形,
.
又点是的中点,
是的中位线,
根据三角形的中位线定理可得:.
则.
故选:B.
【点睛】此题考查了平行四边形的性质:平行四边形的对角线互相平分.还考查了三角形中位线的性质:三角形的中位线平行且等于三角形第三边的一半.本题的关键是熟练掌握三角形中位线的性质.
2.A
【分析】此题考查了三角形中位线的性质,平行四边形的性质,解题的关键是掌握相关基础性质.根据平行四边形的性质可得,再根据三角形中位线的性质,求解即可.
【详解】解:在平行四边形中,,
∴,
∵M,N分别为,的中点,
∴是的中位线,
∴.
故选:A
3.B
【分析】如图,根据三角形中位线定理推出,,则这个四边形是平行四边形,再由对角线垂直,证出,可得这个四边形为矩形.
【详解】解:如图,四边形中,E、F、G、H分别为各边的中点,连接、、、,
∵点E、F、G、H分别为各边的中点,
∴,,,,
∴,,
∴四边形是平行四边形,
∵,,
∴,
∵,
∴,
∴平行四边形是矩形;
故选:B.
【点睛】本题考查了三角形中位线定理、平行四边形的判定以及矩形的判定,正确掌握知识点是解题的关键.
4.A
【分析】依据三角形三边关系,可求第三边大于2小于8,原三角形的周长大于10小于16,连接中点的三角形周长是原三角形周长的一半,那么新三角形的周长应大于5而小于8,看哪个符合就可以了.
【详解】解:设三角形的三边分别是a、b、c,令a=3,b=5,
∵2<c<8,
∴a+b+2<a+b+c<a+b+8,
即10<a+b+c<16,
由三角形中位线的性质可得,中点三角形的三边为、、,
中点三角形的周长为,
∴5<<8.
故选:A.
【点睛】本题考查了三角形中位线定理和三角形三边关系,利用中位线定理求出中点三角形的周长是解题的关键.
5.C
【分析】本题主要考查了全等三角形的性质与判定,三角形中位线定理,延长交于,可证得,得到,可证得是的中位线,从而得出的值,进一步可得出结果.
【详解】解:如图,延长交于,
,
,
在和中,
,
,
,,
,
∴是的中位线,
,
,
故选:C.
6.B
【分析】根据等腰直角三角形的性质得出∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,求出∠APE=∠CPF,证△APE≌△CPF,推出AE=CF,EP=PF,推出S△AEP=S△CPF,求出S四边形AEPF=S△APC=S△ABC,EF不是△ABC的中位线,故EF≠AP,即可得出答案.
【详解】解:∵△ABC中,AB=AC,∠BAC=90°,P是BC中点,
∴∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,
∴∠EPF-∠APF=∠APC-∠APF,
∴∠APE=∠CPF,
在△APE和△CPF中
,
∴△APE≌△CPF(ASA),
∴AE=CF,EP=PF,
∴△EPF是等腰直角三角形,
∴①正确;②正确;
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故③错误;
∵△APE≌△CPF,
∴S△AEP=S△CPF,
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△APF=S△APC=S△ABC,
∴④正确;
∴正确的有①②④,
故选:B.
【点睛】本题考查了等腰三角形性质,三角形中位线的性质,三角形三边关系定理,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.
7.B
【分析】先连接,取其中点,连接、,根据点D、E为线段AC、AO的中点求出DE的长,再根据斜中线定理求出BE的长,当当、、三点在同一条直线上时,BD值最大,求出结果即可.
【详解】解:如下图所示,连接,取其中点,连接、,
∵点D、E为线段AC、AO的中点,
∴,
又∵AB⊥x轴于点B,
∴
∴,
当、、三点在同一条直线上时,BD值最大,
此时;
故选:B.
【点睛】本题主要考查三角形中位线定理、斜中线定理,本题解题的关键是在于找到两点之间线段最短.
8.B
【分析】先根据三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半,即求出原三角形的边长分别为6、8、10,再根据勾股定理的逆定理判断原三角形的形状,即可根据三角形面积公式求得面积.
【详解】解:∵三角形三条中位线的长为3、4、5,
∴原三角形三条边长为,,,
,
∴此三角形为直角三角形,
∴,
故选B.
【点睛】本题考查的是三角形的中位线定理,勾股定理逆定理.熟练掌握三角形的中位线平行于第三边,且等于第三边的一半,是解题的关键.
9.D
【分析】此题考查了三角形中位线定理的应用,由点分别为的中点得到是的三角形中位线,即可得到答案.
【详解】解:∵点分别为的中点,
∴是的三角形中位线,
∴,
故选:D
10.A
【分析】利用中位线、菱形、矩形的性质可知,每一次操作后得到的四边形面积为原四边形面积的一半,由此可解.
【详解】解:如图,连接AC,BD,,.
∵ 四边形ABCD是矩形,
∴,,.
∵ ,,,分别是矩形四个边的中点,
∴,
∴,
∴四边形是菱形,
∵ ,,
∴四边形的面积为:.
同理,由中位线的性质可知,
,,
,,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形,
∴四边形的面积为:.
∴每一次操作后得到的四边形面积为原四边形面积的一半,
∴四边形的面积是.
故选:A.
【点睛】本题考查矩形的性质,菱形的性质以及中位线的性质,证明四边形是菱形,四边形是矩形是解题的关键.
11.D
【分析】本题考查三角形中位线的性质,根据三角形中位线的性质可得四边形的各边长,进而即可求出周长.
【详解】解:∵、是的中位线,
∴,,
,,
∴.
故选:D
12.B
【分析】本题主要考查了三角形的三边关系和全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.根据题意画出图形,设,证明,根据,即可求出答案.
【详解】解:如图所示,取的中点为,连接,,
设,
延长至,使,
在与中,
,
为的中线,
,
,
,
在中,
,
即,
,
故选B.
13.3
【分析】连接CF并延长交AB于G,证明△FDC≌△FBG,根据全等三角形的性质得到BG=DC=6,CF=FG,求出AG,根据三角形中位线定理计算,得到答案.
【详解】解:连接CF并延长交AB于G,
∵AB∥CD,
∴∠FDC=∠FBG,
在△FDC和△FBG中,
,
∴△FDC≌△FBG(ASA)
∴BG=DC=6,CF=FG,
∴AG=AB﹣BG=12﹣6=6,
∵CE=EA,CF=FG,
∴EF=AG=3,
故答案为:3.
【点睛】本题考查的是三角形中位线定理、全等三角形的判定和性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
14.1
【分析】根据三角形中位线定理求出,根据直角三角形的性质求出,计算即可.
【详解】解:∵D、E分别为、的中点,,
∴,
∵,D为的中点,,
∴,
∴,
故答案为:1.
【点睛】本题考查的是三角形中位线定理、直角三角形的性质,解题的关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.
15.2
【分析】根据矩形的性质求出BO长度,然后根据中位线的性质即可得到答案.
【详解】解:∵四边形ABCD是矩形,
∴BD=2BO=8,
∴BO=4,
∵M、N分别为BC、OC的中点,
∴.
故答案为:2.
【点睛】本题主要考查了矩形的性质以及三角形的中位线,解题的关键是找到线段间的倍数关系.
16.44
【详解】∵E、F是AC,CB的中点,
∴EF是△ABC的中位线,
∴EF=AB,
∵EF=22m,
∴AB=44m,
故答案为44.
【点睛】本题考查了三角形的中位线定理在实际生活中的运用,解题的关键是熟知三角形中位线定理的内容.
17.
【详解】解:如图,延长CF交AB于点G,
∵在△AFG和△AFC中,∠GAF=∠CAF,AF=AF,∠AFG=∠AFC,
∴△AFG≌△AFC(ASA).∴AC=AG,GF=CF.
又∵点D是BC中点,∴DF是△CBG的中位线.
∴DF=BG=(AB﹣AG)=(AB﹣AC)=.
故答案为:.
18.(1)见解析;(2)四边形ABPE是平行四边形,理由见解析,BP =5cm;(3),
【分析】(1)证明△AEO△CPO即可说明PO=OE;
(2)证明EP∥AB,即可证明四边形ABPE是平行四边形,利用三角形中位线定理即可求解;
(3)求得四边形ABPE的周长为:6+10+PE=16+PE,得到当PE⊥BC时,PE最小,利用平行四边形的面积公式求得PE,即可求得四边形ABPE的周长最小值,根据△AEO△CPO以及勾股定理即可求得BP的长度.
【详解】(1)证明:∵四边形ABCD是平行四边形,点O为AC的中点,
∴AE∥PC,AO=OC,
∴∠EAO=∠PCO,∠AOE=∠COP,
∴△AEO△CPO,
∴PO=OE;
(2)∵CA⊥AB,且PO⊥AC,
∴PO∥AB,即EP∥AB,
∵四边形ABCD是平行四边形,
∴AE∥BP,
∵CA⊥AB,且AB=6cm,AC=8cm,
∴BC=(cm),
∴四边形ABPE是平行四边形,
∵点O为AC的中点,且PO∥AB,
∴BP=PC=BC=5(cm);
(3)四边形ABPE的周长为:AB+BP+PE+AE,
由(1)知△AEO△CPO,则AE=CP,
∴BP+AE=BP+CP=BC=10,
∴四边形ABPE的周长为:6+10+PE=16+PE,
则PE最小时,四边形ABPE的周长最小,
∴当PE⊥BC时,PE最小(垂线段最短),
∵BCPE=ABAC,
∴PE=(cm),
∴四边形ABPE的周长最小值为16+=(cm),
∵△AEO△CPO,
∴PO=EO=PE=(cm),OC=AC=(cm),
∴PC=(cm),
∴BP=BC-PC=(cm),
故答案为:,.
.
【点睛】本题考查了平行四边形的判定和性质,三角形中位线定理,全等三角形的判定和性质,勾股定理等知识,解题的关键是灵活运用所学知识解决问题.
19.(1)见解析;(2)10.
【分析】(1)根据三角形的中位线性质求出DG∥BC,EF∥BC,DG=BC,EF=BC,求出DG∥EF,DG=EF,根据平行四边形的判定得出即可;
(2)求出∠BOC=90°,根据直角三角形的斜边上中线性质得出EF=2OM,即可求出答案.
【详解】(1)证明: ∵点D、E、F、G分别是AB、OB、OC、AC的中点,
∴DG∥BC,EF∥BC,DG=BC,EF=BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:由 (1)知:四边形DEFG是平行四边形,
∴DG=EF.
∵ ∠OBC与∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°.
∵M为EF的中点,OM=5,
∴OM=EF,即EF=2OM=2×5=10,
∴DG=10.
【点睛】本题考查三角形的中位线性质,平行四边形的判定和性质,直角三角形斜边上中线性质等知识点,能熟练地运用定理进行推理是解题的关键.
20.(1)见解析
(2)2
(3)
【分析】本题考查菱形的性质,平行四边形的判定和性质,中位线的性质等综合题型,解题的关键对菱形性质和图形变化极值情况的熟练掌握.
(1)根据平行四边形判定及性质进行证明即可;
(2)如图,连接,由菱形知,可证,四边形是平行四边形,于是,由勾股定理中,,所以菱形的面积即可求得;
(3)如图,点在延长线上(可以与点重合),得;随着的减小,点逐渐向点接近,当点与点重合时,最小,由矩形性质得,进一步证得,由三角形内角和定理,得,于是.
【详解】(1)证明:∵是的中位线,
∴是中点,
又,
∴四边形是平行四边形,
∴,
∵,
∴,且,
∴四边形是平行四边形,即四边形是平行四边形;
(2)解:如图2,连接,
∵四边形是菱形,
∴,
∴,
∵,
∴,
∵,
∴四边形是平行四边形,
∴,
在中,,
∴,
∵,
∴,
∴,
∴菱形的面积为2;
(3)解:如图,点在延长线上(可以与点重合),
∴,
随着的减小,点逐渐向点接近,当点与点重合时,最小,如图,四边形是矩形,
,
而,
,
,
,
.
21.(1)见解析;(2)4
【分析】(1)连接AD,BC,可证得△APD≌△CPB,从而得到AD=CB.再由三角形中位线定理,可得EG=GF,即可求证;
(2)连接AD、BC交于点M,BC、PD交于点N,可证得△APD≌△CPB,从而得到AD=CB.∠ADP=∠CBP,再由∠CND=∠PNB,AD⊥BC,再由三角形中位线定理,可得△GEF为等腰直角三角形,从而得到,再由,即可求解.
【详解】证明:(1) 如图,连接AD,BC,
∵∠APC=∠BPD,
∴∠APD=∠CPB.
∵PA=PC,PD=PB,
∴△APD≌△CPB,
∴AD=CB.
∵E、G、F分别为AC、CD、DB的中点,
∴EG=AD,GF=BC,
∴EG=GF,
∴∠GEF=∠GFE.
(2)如图,连接AD、BC交于点M,BC、PD交于点N,
∵∠APC=∠BPD=90°,
∴∠APC+∠CPD=∠BPD+∠CPD,即∠APD=∠CPB,
∵PA=PC,PD=PB,
∴△APD≌△CPB(SAS),
∴AD=CB,∠ADP=∠CBP,
∵∠CND=∠PNB,
∴∠DMN=∠BPD=90°,
∴AD⊥BC,
∵E、G、F分别为AC、CD、DB的中点,
∴EG是△ACD的中位线,GF是△DCB的中位线,
∴EG=AD,GF=BC, EGAD,GFBC,
∴GE=GF,GE⊥GF,
∴△GEF为等腰直角三角形,
∴,
∵EF=2,
∴,
∴.
故答案为:4
【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法、等腰直角三角形的性质及三角形中位线的性质是解题的关键.
22.见解析
【分析】本题考查了三角形中位线定理、等腰三角形的判定与性质.三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.根据三角形中位线定理证得是等腰三角形,然后由等腰三角形的性质证得结论.
【详解】证明:∵在四边形中,F、G分别是的中点.
∴是的中位线,
∴.
同理推知,是的中位线,
则.
又∵,
∴,
∴.
23.(1)见解析
(2)
【分析】
本题考查菱形的判定和性质、三角形的中位线定理,平行线的性质,相似三角形的判定和性质等知识
(1)可根据菱形的定义“一组邻边相等的平行四边形是菱形”,先证明四边形是平行四边形,然后再证明四边形的邻边相等即可;
(2)是的中点,有了的长也就求出了菱形的边长的长,那么菱形的周长也就能求出了;
【详解】(1)
证明:、、分别是、、的中点,,,
四边形是平行四边形,
又,,且,
,
四边形是菱形;
(2)
解:,为中点,
,
菱形的周长为.
24.3个,证明见解析.
【详解】试题分析:最多可以有3个平行四边形,是四边形FMHN、四边形EMGN、四边形EFGH,利用三角形中位线定理分别进行证明即可得.
试题解析:最多可以有3个平行四边形,是四边形FMHN、四边形EMGN、四边形EFGH,证明如下:
在四边形ABCD中F,G,H,E,M,N分别是AB,BC,CD,DA,BD,AC的中点,
∴FG∥AC,EH∥AC;FG=AC,EH=AC,
∴FG∥EH,FG=EH,
∴四边形FGHE是平行四边形,
MG∥CD,EN∥CD;MG=CD,EN=CD,
∴MG∥EN,MG=EN ,
∴四边形MGNE是平行四边形,
FM∥AD,NH∥AD;FM=AD,NH=AD,
∴FM∥NH;FM=NH,
∴四边形FMHN是平行四边形,
∴最多可以有3个平行四边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.5三角形的中位线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平行四边形中,对角线、相交于点,为的中点,,则的长为( )
A. B. C. D.
2.如图,在平行四边形中,,E为上一动点,M,N分别为,的中点,则的长为( )
A.3 B.4 C.5 D.不确定
3.顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )
A.正方形 B.矩形 C.菱形 D.梯形
4.如果三角形的两边分别为3和5,那么连结这个三角形三边中点所得三角形的周长可能是( )
A.5.5 B.5 C.4.5 D.4
5.如图,中,,,,,,则的值为( )
A.6 B. C.7 D.8
6.如图,在中,,,直角的顶点是的中点,两边,分别交,于点,.现给出以下四个结论:①;②是等腰直角三角形;③;④.当在内绕顶点旋转时(点不与点,重合),上述结论中始终正确的是( )
A.①②③ B.①②④ C.②③④ D.①③④
7.如图,点A的坐标为(4,3),AB⊥x轴于点B,点C为坐标平面内一点,OC=2,点D为线段AC的中点,连接BD,则BD的最大值为( )
A.3 B. C. D.
8.三角形三条中位线的长为3、4、5,则此三角形的面积为( )
A.12 B.24 C.36 D.48
9.如图,在中,,点分别为的中点,则( )
A. B.1 C.2 D.4
10.如图,已知矩形ABCD的边长分别为a,b,进行如下操作:第一次,顺次连接矩形ABCD各边的中点,得到四边形;第二次,顺次连接四边形各边的中点,得到四边形;…如此反复操作下去,则第n次操作后,得到四边形的面积是( )
A. B. C. D.
11.如图,在中,,,、是的中位线,则四边形的周长是( )
A.5 B.7 C.8 D.10
12.若一个三角形的两边长分别为3和5,则该三角形第三边的中线可以取的值为( )
A.1 B.2 C.4 D.8
二、填空题
13.如图,在四边形ABCD中,AB∥CD,E,F分别是AC,BD的中点,已知AB=12,CD=6,则EF= .
14.如图,在中,D,E分别是,的中点,点F在上,且,若,,则的长为 .
15.如图,在矩形中,,交于点,、分别为、的中点.若,则的长为 .
16.如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=22m,则AB= m.
17.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为 .
三、解答题
18.在学习完了《18.1平行四边形的性质》之后,王老师在数学活动课上对下面一个问题让学生展开探究活动.
问题情境:图1,在 ABCD中,CA⊥AB,AB=6cm,AC=8cm,点O为AC的中点,动点P在BC边上运动,直线PO交AD于E.
问题发现:数学智慧小组”通过积极的动手操作,观察,猜想,提出了如下问题:
(1)在点P运动的过程中,始终存在PO=OE,为什么?
(2)在点P运动到PO⊥AC时,四边形ABPE是平行四边形,为什么?此时BP的长度是多少?
(3)在点P运动的过程中,四边形ABPE的周长是否存在最小值?如果存在,则四边形ABPE的周长的最小值是 cm;BP的长度为 cm.
问题解决:
“数学智慧小组”欢迎您的加入,请开启您的“问题解决之旅”吧!
19.如图,点是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点、、、依次连接,得到四边形.
(1)求证:四边形是平行四边形;
(2)若为的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
20.如图,是的中位线,点为射线上的一个动点(不与点E重合),作交边于点,连结.
(1)如图1,当点M与点D重合时,求证:四边形是平行四边形;
(2)如图,当四边形是菱形时,,求菱形的面积;
(3)如图3,,在延长线上(可以与点D重合),使得四边形为矩形,求的度数范围.
21.(1)探究:如图(1),点P在线段AB上,在AB的同侧作△APC和△BPD,满足PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G分别是AC、BD、CD边中点,连接EF、FG、EG.求证:∠EFG=∠GEF.
(2)应用:如图(2),点P在线段AB上方,∠APC=∠BPD=90°,图(1)题中的其他条件不变,若EF=2,则四边形ABDC的面积为 .
22.已知:如图,在四边形中,,F,G,E分别是的中点.求证:.
23.如图,在中,,、、分别是、、边上的中点.
.
(1)求证:四边形是菱形;
(2)若,求菱形的周长.
24.如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形中,最多可以有几个平行四边形,证明你的结论.
《9.5三角形的中位线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B A C B B B D A
题号 11 12
答案 D B
1.B
【分析】因为四边形是平行四边形,所以;再根据点是的中点,得出是的中位线,即可解决问题.
【详解】四边形是平行四边形,
.
又点是的中点,
是的中位线,
根据三角形的中位线定理可得:.
则.
故选:B.
【点睛】此题考查了平行四边形的性质:平行四边形的对角线互相平分.还考查了三角形中位线的性质:三角形的中位线平行且等于三角形第三边的一半.本题的关键是熟练掌握三角形中位线的性质.
2.A
【分析】此题考查了三角形中位线的性质,平行四边形的性质,解题的关键是掌握相关基础性质.根据平行四边形的性质可得,再根据三角形中位线的性质,求解即可.
【详解】解:在平行四边形中,,
∴,
∵M,N分别为,的中点,
∴是的中位线,
∴.
故选:A
3.B
【分析】如图,根据三角形中位线定理推出,,则这个四边形是平行四边形,再由对角线垂直,证出,可得这个四边形为矩形.
【详解】解:如图,四边形中,E、F、G、H分别为各边的中点,连接、、、,
∵点E、F、G、H分别为各边的中点,
∴,,,,
∴,,
∴四边形是平行四边形,
∵,,
∴,
∵,
∴,
∴平行四边形是矩形;
故选:B.
【点睛】本题考查了三角形中位线定理、平行四边形的判定以及矩形的判定,正确掌握知识点是解题的关键.
4.A
【分析】依据三角形三边关系,可求第三边大于2小于8,原三角形的周长大于10小于16,连接中点的三角形周长是原三角形周长的一半,那么新三角形的周长应大于5而小于8,看哪个符合就可以了.
【详解】解:设三角形的三边分别是a、b、c,令a=3,b=5,
∵2<c<8,
∴a+b+2<a+b+c<a+b+8,
即10<a+b+c<16,
由三角形中位线的性质可得,中点三角形的三边为、、,
中点三角形的周长为,
∴5<<8.
故选:A.
【点睛】本题考查了三角形中位线定理和三角形三边关系,利用中位线定理求出中点三角形的周长是解题的关键.
5.C
【分析】本题主要考查了全等三角形的性质与判定,三角形中位线定理,延长交于,可证得,得到,可证得是的中位线,从而得出的值,进一步可得出结果.
【详解】解:如图,延长交于,
,
,
在和中,
,
,
,,
,
∴是的中位线,
,
,
故选:C.
6.B
【分析】根据等腰直角三角形的性质得出∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,求出∠APE=∠CPF,证△APE≌△CPF,推出AE=CF,EP=PF,推出S△AEP=S△CPF,求出S四边形AEPF=S△APC=S△ABC,EF不是△ABC的中位线,故EF≠AP,即可得出答案.
【详解】解:∵△ABC中,AB=AC,∠BAC=90°,P是BC中点,
∴∠B=∠C=∠BAP=∠CAP=45°,AP=PC=PB,∠APC=∠EPF=90°,
∴∠EPF-∠APF=∠APC-∠APF,
∴∠APE=∠CPF,
在△APE和△CPF中
,
∴△APE≌△CPF(ASA),
∴AE=CF,EP=PF,
∴△EPF是等腰直角三角形,
∴①正确;②正确;
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=BC,
∵EF不是△ABC的中位线,
∴EF≠AP,故③错误;
∵△APE≌△CPF,
∴S△AEP=S△CPF,
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△APF=S△APC=S△ABC,
∴④正确;
∴正确的有①②④,
故选:B.
【点睛】本题考查了等腰三角形性质,三角形中位线的性质,三角形三边关系定理,全等三角形的性质和判定的应用,主要考查学生综合运用性质进行推理的能力.
7.B
【分析】先连接,取其中点,连接、,根据点D、E为线段AC、AO的中点求出DE的长,再根据斜中线定理求出BE的长,当当、、三点在同一条直线上时,BD值最大,求出结果即可.
【详解】解:如下图所示,连接,取其中点,连接、,
∵点D、E为线段AC、AO的中点,
∴,
又∵AB⊥x轴于点B,
∴
∴,
当、、三点在同一条直线上时,BD值最大,
此时;
故选:B.
【点睛】本题主要考查三角形中位线定理、斜中线定理,本题解题的关键是在于找到两点之间线段最短.
8.B
【分析】先根据三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半,即求出原三角形的边长分别为6、8、10,再根据勾股定理的逆定理判断原三角形的形状,即可根据三角形面积公式求得面积.
【详解】解:∵三角形三条中位线的长为3、4、5,
∴原三角形三条边长为,,,
,
∴此三角形为直角三角形,
∴,
故选B.
【点睛】本题考查的是三角形的中位线定理,勾股定理逆定理.熟练掌握三角形的中位线平行于第三边,且等于第三边的一半,是解题的关键.
9.D
【分析】此题考查了三角形中位线定理的应用,由点分别为的中点得到是的三角形中位线,即可得到答案.
【详解】解:∵点分别为的中点,
∴是的三角形中位线,
∴,
故选:D
10.A
【分析】利用中位线、菱形、矩形的性质可知,每一次操作后得到的四边形面积为原四边形面积的一半,由此可解.
【详解】解:如图,连接AC,BD,,.
∵ 四边形ABCD是矩形,
∴,,.
∵ ,,,分别是矩形四个边的中点,
∴,
∴,
∴四边形是菱形,
∵ ,,
∴四边形的面积为:.
同理,由中位线的性质可知,
,,
,,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形,
∴四边形的面积为:.
∴每一次操作后得到的四边形面积为原四边形面积的一半,
∴四边形的面积是.
故选:A.
【点睛】本题考查矩形的性质,菱形的性质以及中位线的性质,证明四边形是菱形,四边形是矩形是解题的关键.
11.D
【分析】本题考查三角形中位线的性质,根据三角形中位线的性质可得四边形的各边长,进而即可求出周长.
【详解】解:∵、是的中位线,
∴,,
,,
∴.
故选:D
12.B
【分析】本题主要考查了三角形的三边关系和全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.根据题意画出图形,设,证明,根据,即可求出答案.
【详解】解:如图所示,取的中点为,连接,,
设,
延长至,使,
在与中,
,
为的中线,
,
,
,
在中,
,
即,
,
故选B.
13.3
【分析】连接CF并延长交AB于G,证明△FDC≌△FBG,根据全等三角形的性质得到BG=DC=6,CF=FG,求出AG,根据三角形中位线定理计算,得到答案.
【详解】解:连接CF并延长交AB于G,
∵AB∥CD,
∴∠FDC=∠FBG,
在△FDC和△FBG中,
,
∴△FDC≌△FBG(ASA)
∴BG=DC=6,CF=FG,
∴AG=AB﹣BG=12﹣6=6,
∵CE=EA,CF=FG,
∴EF=AG=3,
故答案为:3.
【点睛】本题考查的是三角形中位线定理、全等三角形的判定和性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
14.1
【分析】根据三角形中位线定理求出,根据直角三角形的性质求出,计算即可.
【详解】解:∵D、E分别为、的中点,,
∴,
∵,D为的中点,,
∴,
∴,
故答案为:1.
【点睛】本题考查的是三角形中位线定理、直角三角形的性质,解题的关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.
15.2
【分析】根据矩形的性质求出BO长度,然后根据中位线的性质即可得到答案.
【详解】解:∵四边形ABCD是矩形,
∴BD=2BO=8,
∴BO=4,
∵M、N分别为BC、OC的中点,
∴.
故答案为:2.
【点睛】本题主要考查了矩形的性质以及三角形的中位线,解题的关键是找到线段间的倍数关系.
16.44
【详解】∵E、F是AC,CB的中点,
∴EF是△ABC的中位线,
∴EF=AB,
∵EF=22m,
∴AB=44m,
故答案为44.
【点睛】本题考查了三角形的中位线定理在实际生活中的运用,解题的关键是熟知三角形中位线定理的内容.
17.
【详解】解:如图,延长CF交AB于点G,
∵在△AFG和△AFC中,∠GAF=∠CAF,AF=AF,∠AFG=∠AFC,
∴△AFG≌△AFC(ASA).∴AC=AG,GF=CF.
又∵点D是BC中点,∴DF是△CBG的中位线.
∴DF=BG=(AB﹣AG)=(AB﹣AC)=.
故答案为:.
18.(1)见解析;(2)四边形ABPE是平行四边形,理由见解析,BP =5cm;(3),
【分析】(1)证明△AEO△CPO即可说明PO=OE;
(2)证明EP∥AB,即可证明四边形ABPE是平行四边形,利用三角形中位线定理即可求解;
(3)求得四边形ABPE的周长为:6+10+PE=16+PE,得到当PE⊥BC时,PE最小,利用平行四边形的面积公式求得PE,即可求得四边形ABPE的周长最小值,根据△AEO△CPO以及勾股定理即可求得BP的长度.
【详解】(1)证明:∵四边形ABCD是平行四边形,点O为AC的中点,
∴AE∥PC,AO=OC,
∴∠EAO=∠PCO,∠AOE=∠COP,
∴△AEO△CPO,
∴PO=OE;
(2)∵CA⊥AB,且PO⊥AC,
∴PO∥AB,即EP∥AB,
∵四边形ABCD是平行四边形,
∴AE∥BP,
∵CA⊥AB,且AB=6cm,AC=8cm,
∴BC=(cm),
∴四边形ABPE是平行四边形,
∵点O为AC的中点,且PO∥AB,
∴BP=PC=BC=5(cm);
(3)四边形ABPE的周长为:AB+BP+PE+AE,
由(1)知△AEO△CPO,则AE=CP,
∴BP+AE=BP+CP=BC=10,
∴四边形ABPE的周长为:6+10+PE=16+PE,
则PE最小时,四边形ABPE的周长最小,
∴当PE⊥BC时,PE最小(垂线段最短),
∵BCPE=ABAC,
∴PE=(cm),
∴四边形ABPE的周长最小值为16+=(cm),
∵△AEO△CPO,
∴PO=EO=PE=(cm),OC=AC=(cm),
∴PC=(cm),
∴BP=BC-PC=(cm),
故答案为:,.
.
【点睛】本题考查了平行四边形的判定和性质,三角形中位线定理,全等三角形的判定和性质,勾股定理等知识,解题的关键是灵活运用所学知识解决问题.
19.(1)见解析;(2)10.
【分析】(1)根据三角形的中位线性质求出DG∥BC,EF∥BC,DG=BC,EF=BC,求出DG∥EF,DG=EF,根据平行四边形的判定得出即可;
(2)求出∠BOC=90°,根据直角三角形的斜边上中线性质得出EF=2OM,即可求出答案.
【详解】(1)证明: ∵点D、E、F、G分别是AB、OB、OC、AC的中点,
∴DG∥BC,EF∥BC,DG=BC,EF=BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:由 (1)知:四边形DEFG是平行四边形,
∴DG=EF.
∵ ∠OBC与∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°.
∵M为EF的中点,OM=5,
∴OM=EF,即EF=2OM=2×5=10,
∴DG=10.
【点睛】本题考查三角形的中位线性质,平行四边形的判定和性质,直角三角形斜边上中线性质等知识点,能熟练地运用定理进行推理是解题的关键.
20.(1)见解析
(2)2
(3)
【分析】本题考查菱形的性质,平行四边形的判定和性质,中位线的性质等综合题型,解题的关键对菱形性质和图形变化极值情况的熟练掌握.
(1)根据平行四边形判定及性质进行证明即可;
(2)如图,连接,由菱形知,可证,四边形是平行四边形,于是,由勾股定理中,,所以菱形的面积即可求得;
(3)如图,点在延长线上(可以与点重合),得;随着的减小,点逐渐向点接近,当点与点重合时,最小,由矩形性质得,进一步证得,由三角形内角和定理,得,于是.
【详解】(1)证明:∵是的中位线,
∴是中点,
又,
∴四边形是平行四边形,
∴,
∵,
∴,且,
∴四边形是平行四边形,即四边形是平行四边形;
(2)解:如图2,连接,
∵四边形是菱形,
∴,
∴,
∵,
∴,
∵,
∴四边形是平行四边形,
∴,
在中,,
∴,
∵,
∴,
∴,
∴菱形的面积为2;
(3)解:如图,点在延长线上(可以与点重合),
∴,
随着的减小,点逐渐向点接近,当点与点重合时,最小,如图,四边形是矩形,
,
而,
,
,
,
.
21.(1)见解析;(2)4
【分析】(1)连接AD,BC,可证得△APD≌△CPB,从而得到AD=CB.再由三角形中位线定理,可得EG=GF,即可求证;
(2)连接AD、BC交于点M,BC、PD交于点N,可证得△APD≌△CPB,从而得到AD=CB.∠ADP=∠CBP,再由∠CND=∠PNB,AD⊥BC,再由三角形中位线定理,可得△GEF为等腰直角三角形,从而得到,再由,即可求解.
【详解】证明:(1) 如图,连接AD,BC,
∵∠APC=∠BPD,
∴∠APD=∠CPB.
∵PA=PC,PD=PB,
∴△APD≌△CPB,
∴AD=CB.
∵E、G、F分别为AC、CD、DB的中点,
∴EG=AD,GF=BC,
∴EG=GF,
∴∠GEF=∠GFE.
(2)如图,连接AD、BC交于点M,BC、PD交于点N,
∵∠APC=∠BPD=90°,
∴∠APC+∠CPD=∠BPD+∠CPD,即∠APD=∠CPB,
∵PA=PC,PD=PB,
∴△APD≌△CPB(SAS),
∴AD=CB,∠ADP=∠CBP,
∵∠CND=∠PNB,
∴∠DMN=∠BPD=90°,
∴AD⊥BC,
∵E、G、F分别为AC、CD、DB的中点,
∴EG是△ACD的中位线,GF是△DCB的中位线,
∴EG=AD,GF=BC, EGAD,GFBC,
∴GE=GF,GE⊥GF,
∴△GEF为等腰直角三角形,
∴,
∵EF=2,
∴,
∴.
故答案为:4
【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法、等腰直角三角形的性质及三角形中位线的性质是解题的关键.
22.见解析
【分析】本题考查了三角形中位线定理、等腰三角形的判定与性质.三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.根据三角形中位线定理证得是等腰三角形,然后由等腰三角形的性质证得结论.
【详解】证明:∵在四边形中,F、G分别是的中点.
∴是的中位线,
∴.
同理推知,是的中位线,
则.
又∵,
∴,
∴.
23.(1)见解析
(2)
【分析】
本题考查菱形的判定和性质、三角形的中位线定理,平行线的性质,相似三角形的判定和性质等知识
(1)可根据菱形的定义“一组邻边相等的平行四边形是菱形”,先证明四边形是平行四边形,然后再证明四边形的邻边相等即可;
(2)是的中点,有了的长也就求出了菱形的边长的长,那么菱形的周长也就能求出了;
【详解】(1)
证明:、、分别是、、的中点,,,
四边形是平行四边形,
又,,且,
,
四边形是菱形;
(2)
解:,为中点,
,
菱形的周长为.
24.3个,证明见解析.
【详解】试题分析:最多可以有3个平行四边形,是四边形FMHN、四边形EMGN、四边形EFGH,利用三角形中位线定理分别进行证明即可得.
试题解析:最多可以有3个平行四边形,是四边形FMHN、四边形EMGN、四边形EFGH,证明如下:
在四边形ABCD中F,G,H,E,M,N分别是AB,BC,CD,DA,BD,AC的中点,
∴FG∥AC,EH∥AC;FG=AC,EH=AC,
∴FG∥EH,FG=EH,
∴四边形FGHE是平行四边形,
MG∥CD,EN∥CD;MG=CD,EN=CD,
∴MG∥EN,MG=EN ,
∴四边形MGNE是平行四边形,
FM∥AD,NH∥AD;FM=AD,NH=AD,
∴FM∥NH;FM=NH,
∴四边形FMHN是平行四边形,
∴最多可以有3个平行四边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
