人教版数学九上课件25.2 用列举法求概率(共27张PPT)
文档属性
| 名称 | 人教版数学九上课件25.2 用列举法求概率(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 664.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-12 13:53:41 | ||
图片预览







文档简介
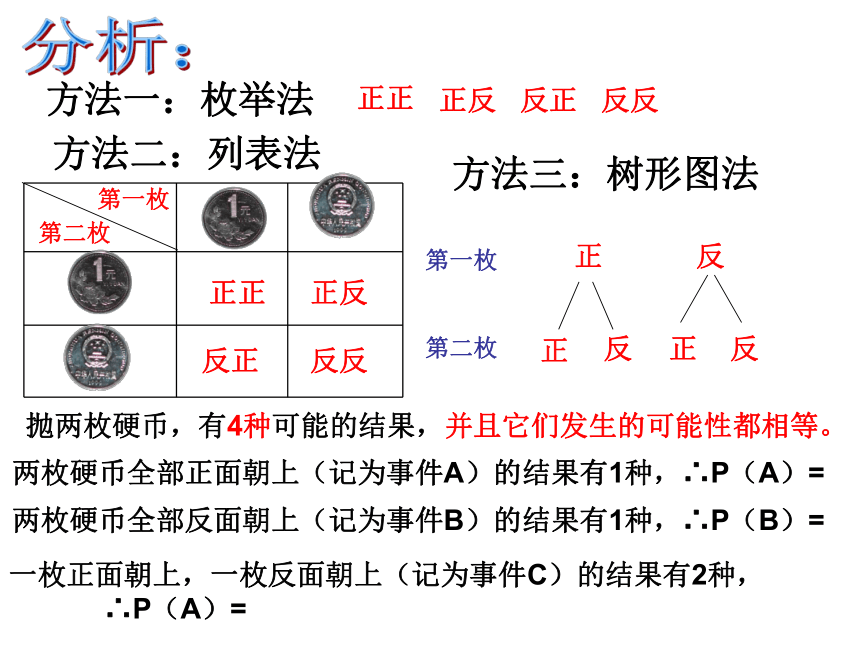
课件27张PPT。25.2 用列举法求概率 在一次试验中,如果可能出现的结果只有____个,且各种结果出现的可能性大小____,我们可以通过列举试验结果的方法,分析出随机事件发生的概率。用列举法求概率有限相等评选数学电脑保管员胡逸飞王一帆张舒彬评选数学电脑保管员魏芷毓汤若琪李悦童方法一:枚举法分析:方法二:列表法第一枚第二枚正正反正正反反反正正正反反正反反方法三:树形图法第一枚第二枚正反正反正反抛两枚硬币,有4种可能的结果,并且它们发生的可能性都相等。两枚硬币全部正面朝上(记为事件A)的结果有1种,∴P(A)=两枚硬币全部反面朝上(记为事件B)的结果有1种,∴P(B)=一枚正面朝上,一枚反面朝上(记为事件C)的结果有2种,
∴P(A)=1.袋子中装有红,绿各一个小球,除颜色外无其他差别,随机摸出1个小球后放回,再随机摸出一个.求下列事件的概率: (1)第一次摸到红球,第二次摸到绿球; (2)两次都摸到相同颜色的小球; (3)两次摸到的球中有一个绿球和一个红球. 练一练变式1:若再放入两个红球,一个绿球,一个黄球呢?
变式2:在变式1的基础上随机摸出1个小球后不放回,再随机摸出一个呢?
变式3:在变式1的基础上随机摸出两个小球呢?
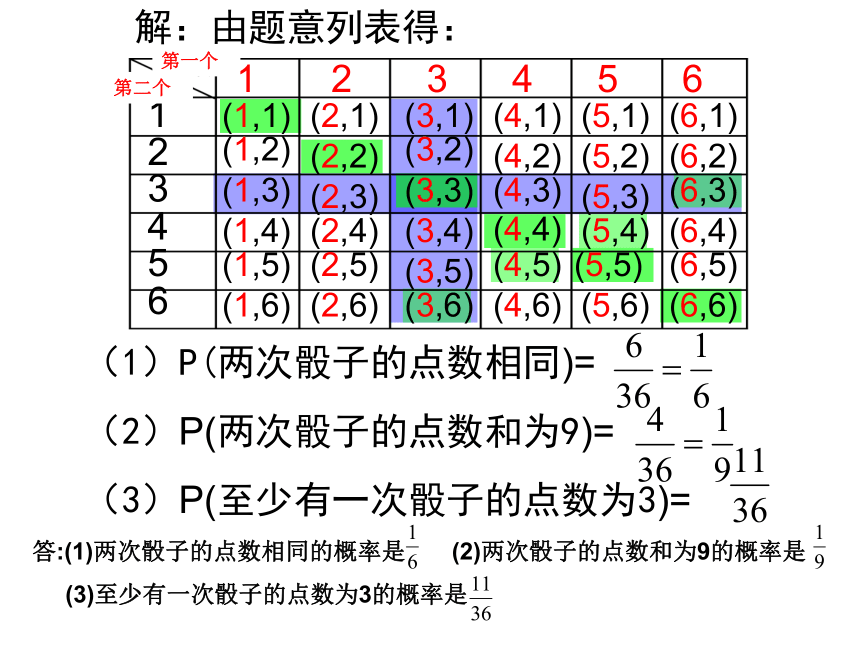
同时投掷两个质地均匀的骰子,观察向上一面的点数,求下列事件的概率. (1)两个骰子的点数相同; (2)两个骰子点数的和是9; ⑶至少有一个骰子的点数为2; 练一练解:由题意列表得: 1 2 3 4 5 6(1)P(两次骰子的点数相同)=
(2)P(两次骰子的点数和为9)=
(3)P(至少有一次骰子的点数为3)=第一个第二个1 2 3 4 5 6解:根据题意,画出如下树形图: 第一个第二个(1)P(两次骰子的点数相同)=
(2)P(两次骰子的点数和为9)=
(3)P(至少有一次骰子的点数为3)= 当一次试验要涉及两个因素(如:同时掷两个骰子)或一个因素做两次试验(如:一个骰子掷两次)并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常可以采用列表法,也可以用树形图。总结想一想: 如果把上题中的“同时掷两个骰子”改为
“把一个骰子掷两次”,所得的结果有变化吗?
没有变化这个游戏对小亮和小明公平吗?
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”。如果你是小亮,你愿意接受这个游戏的规则吗? 为什么?试一试:解:我不愿意接受这个游戏的规则,理由如下:
列表: 由表中可以看出,在两堆牌中分别取一张,它可能出现的结果有36个,它们出现的可能性相等。1 2 3 4 5 6解:根据题意,画出如下树形图: 红桃黑桃 由树形图可以看出,在两堆牌中分别取一张,有36种可能的结果,并且它们发生的可能性都相等。 满足两张牌的数字之积为奇数(记为事件A)
的结果有9种,所以P(A)=
满足两张牌的数字之积为偶数(记为事件B)
的结果有27种,所以 P(B)=因为P(A) < P(B),所以如果我是小亮,
我不愿意接受这个游戏的规则。例1、甲口袋中装有2个相同的小球,它们分别写有字母A和B; 乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I。从3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少? 用列举法求概率本题中元音字母: A E I 辅音字母: B C D H甲口袋中装有2个相同的小球,它们分别写有字母A和B; 乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I。 从3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少? 甲乙丙ACDEHIHIHIBCDEHIHIHI解:由树形图得,有12种可能的结果,并且它们发生的可能性都相等。
(1)只有一个元音字母(记为事件A)的结果有5种,则 P(A)=
只有两个元音字母(记为事件B)的结果有4种,则 P(B)= =
三个全部为元音字母(记为事件C)的结果有1种,则 P(C)=
(2)全是辅音字母(记为事件D)的结果有2种,则 P(D)= = 当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.一个因素所包含的可能情况 另一个因素所包含的可能情况两个因素所组合的所有可能情况,即n 在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.列表法中表格构造特点: 当一次试验中涉及3个因素或更多的因素时,怎么办?想一想,什么时候用“列表法”方便,什么时候用“树形图”方便?当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为不重复不遗漏地列出所有可能的结果,通常用树形图用列举法求概率例2.同时抛掷三枚硬币,求下列事件的概率:
(1) 三枚硬币全部正面朝上;
(2) 两枚硬币正面朝上而一枚硬币反面朝上;
(3) 至少有两枚硬币正面朝上.正反正反正反正反正反正反正反抛掷硬币试验解: 由树形图可以看出,抛掷3枚硬币有8种可能的结果,并且它们发生的可能性都相等.∴ P(A)(1)满足三枚硬币全部正面朝上(记为事件A)的结果有1种∴ P(B)(2)满足两枚硬币正面朝上而一枚硬币反面朝上(记为事件B)的结果有3种(3)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种∴ P(C)第①枚②③练习:经过某十字路口的汽车,它可能继续直行,也可能左转或右转,如果这三种可能性大小相同,同向而行的三辆汽车都经过这个十字路口时,求下列事件的概率:(1)三辆车全部继续直行(2)两辆车右转,一辆车左转(3)至少有两辆车左转 解:由树形图得,所有可能出现的结果有27个,它们出现的可能性相等。
(1)三辆车全部继续直行的结果有1个,则 P(三辆车全部继续直行)=
(2)两辆车右转,一辆车左转的结果有3个,则
P(两辆车右转,一辆车左转)= =
(3)至少有两辆车左转的结果有7个,则 P(至少有两辆车左转)=第一辆车第二辆车第三辆车1.甲、乙、丙三个同学排成一排拍照,则甲
排在中间的概率是( );
2.某市医院决定从内科5位骨科医师中(含有甲)抽调3人成立防控小组,则甲一定抽调到防控小组的概率是( );
3.甲、乙、丙、丁四名运动员参加接力赛,甲必须为第一接力或第四接力棒的运用员,那么这四名运动员在比赛过程中的接力顺序有( )种;
4.亮亮、兵兵和军军都有一套外形完全相同,背面分别写有“祝福”、“北京”、“奥运”字样的三张卡片,他们分别从自己的一套卡片中随机抽取一张,抽取的三张卡片中正好分别含有“祝福”,“北京”,“奥运”的概率是( ).5.甲、乙、丙三人打乒乓球.由哪两人先打呢?他们决定用 “石头、剪刀、布”的游戏来决定,游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 问一次比赛能淘汰一人的概率是多少?解: 戏的结果有27种,它们出现的可能性相等. 由规则可知,一次能淘汰一人的结果应是:“石石剪” “剪剪布” “布布石”三类. 有树状图可以看出,游 而满足条件(记为事件A)的结果有9种∴ P(A)=6.某人有5把钥匙,但忘记了开房门的是哪一把,于是,他逐把不重复地试开,问
(1)恰好第三次打开房门锁的概率是多少?
(2)三次内打开的概率是多少?
(3)如果5把内有2把房门钥匙,那么三次内打开的概率是多少?8.一张圆桌旁有四个座位,A先坐在如图所示的座位上,B.C.D三人随机坐到其他三个座位上.则A与B不相邻而坐的概率为___;7.将三个均匀的六面分别标有1,2,3,4,5,6的正方体同时掷出,出现的数字分别为a、b、c,则a、b、c正好是直角三角形三边长的概率是___;9、在一个口袋中有5个完全相同的小球,把它们分别标号1,2,3,4,5,随机地摸出一个小球后放回,再随机地摸出一个小球,用列表法求下列事件的概率
(1)两次取的小球的标号相同;
(2)两次取的小球的标号的和等于5;这节课你有什么收获?作业课本P138-P139
3,4,5,6,7,8,9
不抄题,写清页数题号.
第4题直接写答案;
3,5,6,7,8画树形图或列表做.
∴P(A)=1.袋子中装有红,绿各一个小球,除颜色外无其他差别,随机摸出1个小球后放回,再随机摸出一个.求下列事件的概率: (1)第一次摸到红球,第二次摸到绿球; (2)两次都摸到相同颜色的小球; (3)两次摸到的球中有一个绿球和一个红球. 练一练变式1:若再放入两个红球,一个绿球,一个黄球呢?
变式2:在变式1的基础上随机摸出1个小球后不放回,再随机摸出一个呢?
变式3:在变式1的基础上随机摸出两个小球呢?
同时投掷两个质地均匀的骰子,观察向上一面的点数,求下列事件的概率. (1)两个骰子的点数相同; (2)两个骰子点数的和是9; ⑶至少有一个骰子的点数为2; 练一练解:由题意列表得: 1 2 3 4 5 6(1)P(两次骰子的点数相同)=
(2)P(两次骰子的点数和为9)=
(3)P(至少有一次骰子的点数为3)=第一个第二个1 2 3 4 5 6解:根据题意,画出如下树形图: 第一个第二个(1)P(两次骰子的点数相同)=
(2)P(两次骰子的点数和为9)=
(3)P(至少有一次骰子的点数为3)= 当一次试验要涉及两个因素(如:同时掷两个骰子)或一个因素做两次试验(如:一个骰子掷两次)并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常可以采用列表法,也可以用树形图。总结想一想: 如果把上题中的“同时掷两个骰子”改为
“把一个骰子掷两次”,所得的结果有变化吗?
没有变化这个游戏对小亮和小明公平吗?
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”。如果你是小亮,你愿意接受这个游戏的规则吗? 为什么?试一试:解:我不愿意接受这个游戏的规则,理由如下:
列表: 由表中可以看出,在两堆牌中分别取一张,它可能出现的结果有36个,它们出现的可能性相等。1 2 3 4 5 6解:根据题意,画出如下树形图: 红桃黑桃 由树形图可以看出,在两堆牌中分别取一张,有36种可能的结果,并且它们发生的可能性都相等。 满足两张牌的数字之积为奇数(记为事件A)
的结果有9种,所以P(A)=
满足两张牌的数字之积为偶数(记为事件B)
的结果有27种,所以 P(B)=因为P(A) < P(B),所以如果我是小亮,
我不愿意接受这个游戏的规则。例1、甲口袋中装有2个相同的小球,它们分别写有字母A和B; 乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I。从3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少? 用列举法求概率本题中元音字母: A E I 辅音字母: B C D H甲口袋中装有2个相同的小球,它们分别写有字母A和B; 乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I。 从3个口袋中各随机地取出1个小球。
(1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少? 甲乙丙ACDEHIHIHIBCDEHIHIHI解:由树形图得,有12种可能的结果,并且它们发生的可能性都相等。
(1)只有一个元音字母(记为事件A)的结果有5种,则 P(A)=
只有两个元音字母(记为事件B)的结果有4种,则 P(B)= =
三个全部为元音字母(记为事件C)的结果有1种,则 P(C)=
(2)全是辅音字母(记为事件D)的结果有2种,则 P(D)= = 当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.一个因素所包含的可能情况 另一个因素所包含的可能情况两个因素所组合的所有可能情况,即n 在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.列表法中表格构造特点: 当一次试验中涉及3个因素或更多的因素时,怎么办?想一想,什么时候用“列表法”方便,什么时候用“树形图”方便?当一次试验涉及两个因素时,且可能出现的结果较多时,为不重复不遗漏地列出所有可能的结果,通常用列表法当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为不重复不遗漏地列出所有可能的结果,通常用树形图用列举法求概率例2.同时抛掷三枚硬币,求下列事件的概率:
(1) 三枚硬币全部正面朝上;
(2) 两枚硬币正面朝上而一枚硬币反面朝上;
(3) 至少有两枚硬币正面朝上.正反正反正反正反正反正反正反抛掷硬币试验解: 由树形图可以看出,抛掷3枚硬币有8种可能的结果,并且它们发生的可能性都相等.∴ P(A)(1)满足三枚硬币全部正面朝上(记为事件A)的结果有1种∴ P(B)(2)满足两枚硬币正面朝上而一枚硬币反面朝上(记为事件B)的结果有3种(3)满足至少有两枚硬币正面朝上(记为事件C)的结果有4种∴ P(C)第①枚②③练习:经过某十字路口的汽车,它可能继续直行,也可能左转或右转,如果这三种可能性大小相同,同向而行的三辆汽车都经过这个十字路口时,求下列事件的概率:(1)三辆车全部继续直行(2)两辆车右转,一辆车左转(3)至少有两辆车左转 解:由树形图得,所有可能出现的结果有27个,它们出现的可能性相等。
(1)三辆车全部继续直行的结果有1个,则 P(三辆车全部继续直行)=
(2)两辆车右转,一辆车左转的结果有3个,则
P(两辆车右转,一辆车左转)= =
(3)至少有两辆车左转的结果有7个,则 P(至少有两辆车左转)=第一辆车第二辆车第三辆车1.甲、乙、丙三个同学排成一排拍照,则甲
排在中间的概率是( );
2.某市医院决定从内科5位骨科医师中(含有甲)抽调3人成立防控小组,则甲一定抽调到防控小组的概率是( );
3.甲、乙、丙、丁四名运动员参加接力赛,甲必须为第一接力或第四接力棒的运用员,那么这四名运动员在比赛过程中的接力顺序有( )种;
4.亮亮、兵兵和军军都有一套外形完全相同,背面分别写有“祝福”、“北京”、“奥运”字样的三张卡片,他们分别从自己的一套卡片中随机抽取一张,抽取的三张卡片中正好分别含有“祝福”,“北京”,“奥运”的概率是( ).5.甲、乙、丙三人打乒乓球.由哪两人先打呢?他们决定用 “石头、剪刀、布”的游戏来决定,游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 问一次比赛能淘汰一人的概率是多少?解: 戏的结果有27种,它们出现的可能性相等. 由规则可知,一次能淘汰一人的结果应是:“石石剪” “剪剪布” “布布石”三类. 有树状图可以看出,游 而满足条件(记为事件A)的结果有9种∴ P(A)=6.某人有5把钥匙,但忘记了开房门的是哪一把,于是,他逐把不重复地试开,问
(1)恰好第三次打开房门锁的概率是多少?
(2)三次内打开的概率是多少?
(3)如果5把内有2把房门钥匙,那么三次内打开的概率是多少?8.一张圆桌旁有四个座位,A先坐在如图所示的座位上,B.C.D三人随机坐到其他三个座位上.则A与B不相邻而坐的概率为___;7.将三个均匀的六面分别标有1,2,3,4,5,6的正方体同时掷出,出现的数字分别为a、b、c,则a、b、c正好是直角三角形三边长的概率是___;9、在一个口袋中有5个完全相同的小球,把它们分别标号1,2,3,4,5,随机地摸出一个小球后放回,再随机地摸出一个小球,用列表法求下列事件的概率
(1)两次取的小球的标号相同;
(2)两次取的小球的标号的和等于5;这节课你有什么收获?作业课本P138-P139
3,4,5,6,7,8,9
不抄题,写清页数题号.
第4题直接写答案;
3,5,6,7,8画树形图或列表做.
同课章节目录
