人教版数学九下课件 第二十八章《锐角三角函数》小结与复习 (共14张PPT)
文档属性
| 名称 | 人教版数学九下课件 第二十八章《锐角三角函数》小结与复习 (共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 577.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-12 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
小结与复习(3)
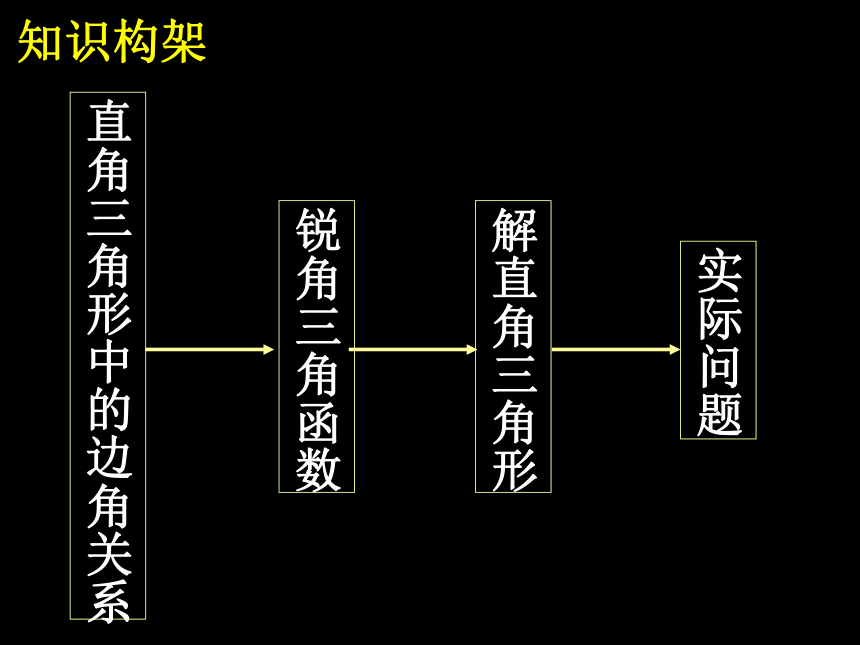
知识构架
锐角三角函数
直角三角形中的边角关系
解直角三角形
实际问题
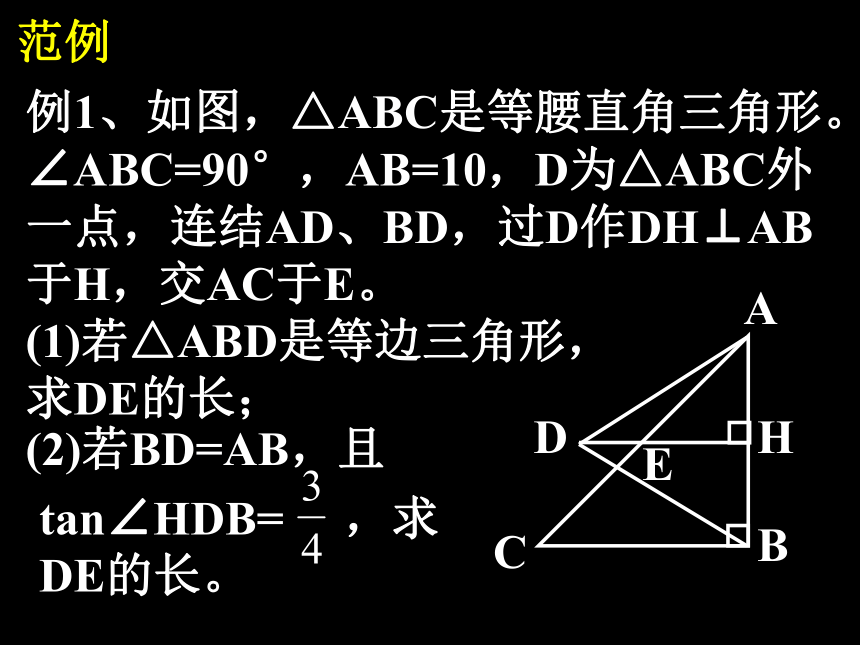
例1、如图,△ABC是等腰直角三角形。
∠ABC=90°,AB=10,D为△ABC外
一点,连结AD、BD,过D作DH⊥AB
于H,交AC于E。
(1)若△ABD是等边三角形,
求DE的长;
范例
(2)若BD=AB,且
C
A
B
D
H
E
tan∠HDB= ,求
DE的长。
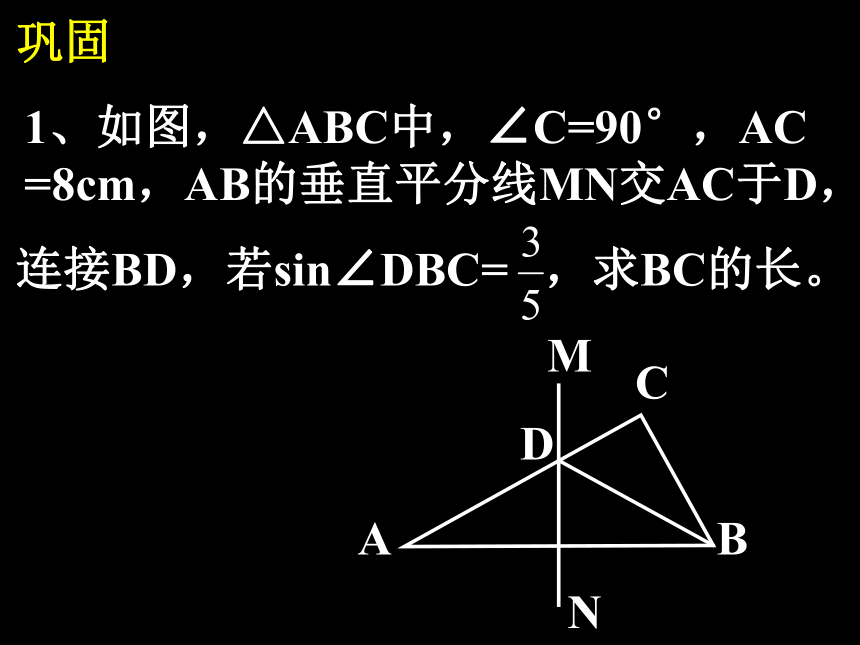
巩固
1、如图,△ABC中,∠C=90°,AC
=8cm,AB的垂直平分线MN交AC于D,
连接BD,若sin∠DBC= ,求BC的长。
C
A
B
D
M
N
巩固
2、如图,AD⊥CD, AB=10,BC=20,
∠A=C=30°,求AD、CD的长。
B
A
C
D
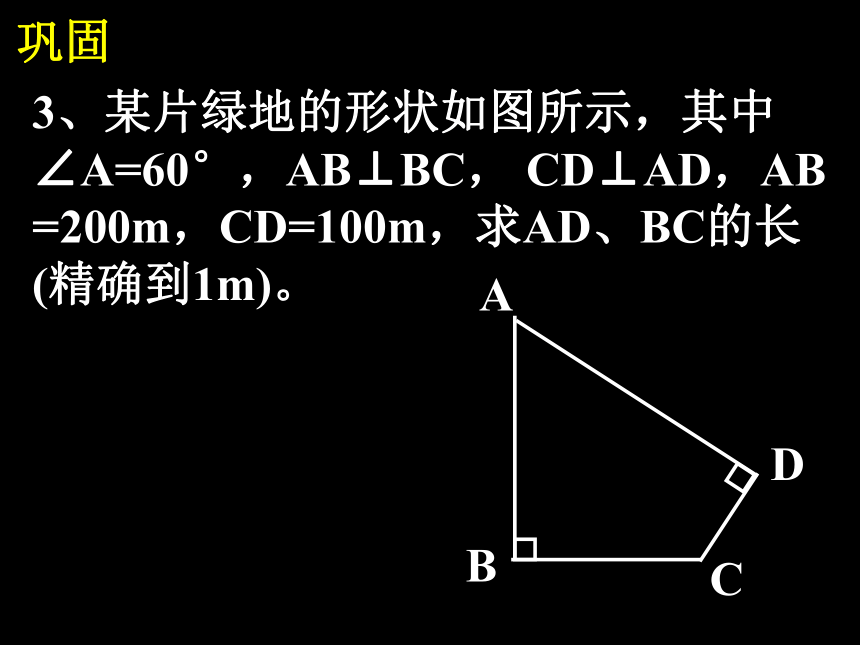
巩固
3、某片绿地的形状如图所示,其中
∠A=60°,AB⊥BC, CD⊥AD,AB
=200m,CD=100m,求AD、BC的长
(精确到1m)。
B
A
C
D
范例
例2、如图,AB是⊙O的切线,A为切
点,AC是⊙O的弦,过O作OH ⊥ AC
于H,OH=2,AB=12,BO=13,求:
(1) ⊙O的半径;
(2)sin∠OAC的值;
(3)弦AC的长(结果保
留两个有效数字)。
A
B
O
C
H
巩固
4、如图,某海域直径为30海里的暗礁区中
心有一哨所A,值班人员发现一轮船从哨所
正西方向90海里的B处向哨所驶来,哨所及
时向轮船发出了危险信号,但轮船没有收
到信号,又继续前进了15海里到达C处,此
时哨所发出第二次紧急信号。(1)若轮船收
到第一次信号后,为避免触礁,
航向改变角度至少为东偏北
α度,求
sinα的值。
A
B
C
巩固
4、如图,某海域直径为30海里的暗礁区中
心有一哨所A,值班人员发现一轮船从哨所
正西方向90海里的B处向哨所驶来,哨所及
时向轮船发出了危险信号,但轮船没有收
到信号,又继续前进了15海里到达C处,此
时哨所发出第二次紧急信号。(2)当轮船收
到第二次信号后,为避免触礁,
航向改变的角度至少为多少度
(结果保留小
数点后两位)。
A
B
C
范例
例3、某学校拟建两幢平行的教学楼,
现设计两楼相距30m。从A点看C点,
仰角为5°;从A点看D点,俯角为
30°。
(1)两幢楼分别高多
少米(精确到1m)?
30°
A
C
B
D
5°
30°
1
号
楼
2
号
楼
范例
(2)若冬日上午9∶00太阳光的入射角最
低为30°(光线与水平线的夹角),问1
号楼是否会有影响?请说明理由。若
有,则两楼间距离应至少相距多少米
时才会消除这种影响?
30°
A
C
B
D
5°
30°
1
号
楼
2
号
楼
巩固
5、如图,某货船以20海里/h的速度将一批
重要物资由A处运往正西方向的B处,经过
16h的航行到达,到达后必须立即卸货。此
时,接到气象部门通知,一台风中心正以
40海里/h的速度由A处北偏西60°方向移动,
距台风中心200海里的圆形区域(包括边界)
均会受到影响。
A
B
C
北
西
60°
(1)B处是否会受到台
风的影响?请说明理
由。
巩固
5、如图,某货船以20海里/h的速度将一批
重要物资由A处运往正西方向的B处,经过
16h的航行到达,到达后必须立即卸货。此
时,接到气象部门通知,一台风中心正以
40海里/h的速度由A处北偏西60°方向移动,
距台风中心200海里的圆形区域(包括边界)
均会受到影响。
A
B
C
北
西
60°
(2)为避免受到台风
的影响,该船应在多
少小时内卸完货物?
小结
锐角三角函数
直角三角形中的边角关系
解直角三角形
实际问题
小结与复习(3)
知识构架
锐角三角函数
直角三角形中的边角关系
解直角三角形
实际问题
例1、如图,△ABC是等腰直角三角形。
∠ABC=90°,AB=10,D为△ABC外
一点,连结AD、BD,过D作DH⊥AB
于H,交AC于E。
(1)若△ABD是等边三角形,
求DE的长;
范例
(2)若BD=AB,且
C
A
B
D
H
E
tan∠HDB= ,求
DE的长。
巩固
1、如图,△ABC中,∠C=90°,AC
=8cm,AB的垂直平分线MN交AC于D,
连接BD,若sin∠DBC= ,求BC的长。
C
A
B
D
M
N
巩固
2、如图,AD⊥CD, AB=10,BC=20,
∠A=C=30°,求AD、CD的长。
B
A
C
D
巩固
3、某片绿地的形状如图所示,其中
∠A=60°,AB⊥BC, CD⊥AD,AB
=200m,CD=100m,求AD、BC的长
(精确到1m)。
B
A
C
D
范例
例2、如图,AB是⊙O的切线,A为切
点,AC是⊙O的弦,过O作OH ⊥ AC
于H,OH=2,AB=12,BO=13,求:
(1) ⊙O的半径;
(2)sin∠OAC的值;
(3)弦AC的长(结果保
留两个有效数字)。
A
B
O
C
H
巩固
4、如图,某海域直径为30海里的暗礁区中
心有一哨所A,值班人员发现一轮船从哨所
正西方向90海里的B处向哨所驶来,哨所及
时向轮船发出了危险信号,但轮船没有收
到信号,又继续前进了15海里到达C处,此
时哨所发出第二次紧急信号。(1)若轮船收
到第一次信号后,为避免触礁,
航向改变角度至少为东偏北
α度,求
sinα的值。
A
B
C
巩固
4、如图,某海域直径为30海里的暗礁区中
心有一哨所A,值班人员发现一轮船从哨所
正西方向90海里的B处向哨所驶来,哨所及
时向轮船发出了危险信号,但轮船没有收
到信号,又继续前进了15海里到达C处,此
时哨所发出第二次紧急信号。(2)当轮船收
到第二次信号后,为避免触礁,
航向改变的角度至少为多少度
(结果保留小
数点后两位)。
A
B
C
范例
例3、某学校拟建两幢平行的教学楼,
现设计两楼相距30m。从A点看C点,
仰角为5°;从A点看D点,俯角为
30°。
(1)两幢楼分别高多
少米(精确到1m)?
30°
A
C
B
D
5°
30°
1
号
楼
2
号
楼
范例
(2)若冬日上午9∶00太阳光的入射角最
低为30°(光线与水平线的夹角),问1
号楼是否会有影响?请说明理由。若
有,则两楼间距离应至少相距多少米
时才会消除这种影响?
30°
A
C
B
D
5°
30°
1
号
楼
2
号
楼
巩固
5、如图,某货船以20海里/h的速度将一批
重要物资由A处运往正西方向的B处,经过
16h的航行到达,到达后必须立即卸货。此
时,接到气象部门通知,一台风中心正以
40海里/h的速度由A处北偏西60°方向移动,
距台风中心200海里的圆形区域(包括边界)
均会受到影响。
A
B
C
北
西
60°
(1)B处是否会受到台
风的影响?请说明理
由。
巩固
5、如图,某货船以20海里/h的速度将一批
重要物资由A处运往正西方向的B处,经过
16h的航行到达,到达后必须立即卸货。此
时,接到气象部门通知,一台风中心正以
40海里/h的速度由A处北偏西60°方向移动,
距台风中心200海里的圆形区域(包括边界)
均会受到影响。
A
B
C
北
西
60°
(2)为避免受到台风
的影响,该船应在多
少小时内卸完货物?
小结
锐角三角函数
直角三角形中的边角关系
解直角三角形
实际问题
