人教A版高中数学选修2-1课件:2.4.1 抛物线及其标准方程(公开课)(共20张PPT)
文档属性
| 名称 | 人教A版高中数学选修2-1课件:2.4.1 抛物线及其标准方程(公开课)(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 560.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-11 22:03:58 | ||
图片预览





文档简介
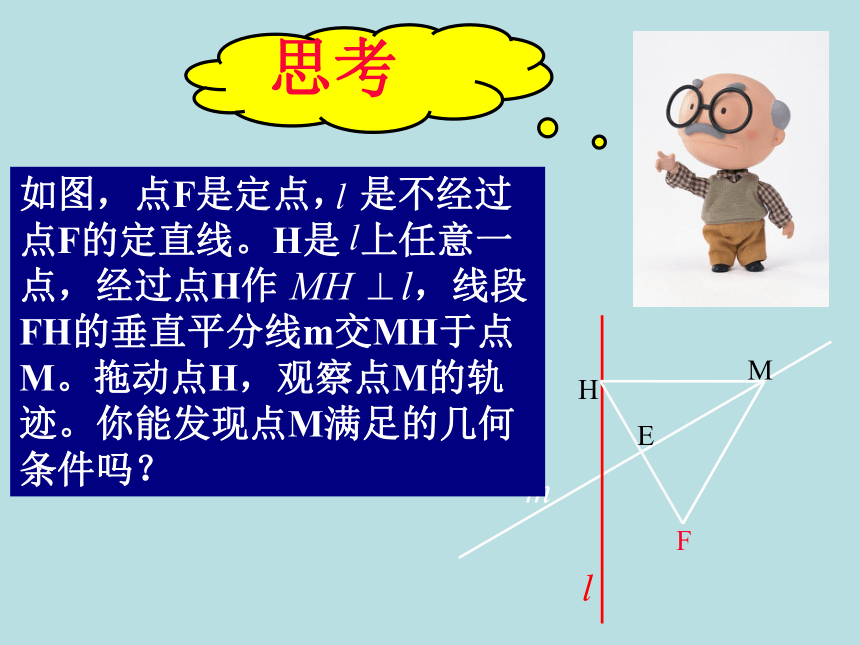
课件20张PPT。抛物线及其标准方程人教A版高中数学选修2-1 思考定 H定点F叫做抛物线的焦点。义
思 考:如何建立适当的直角
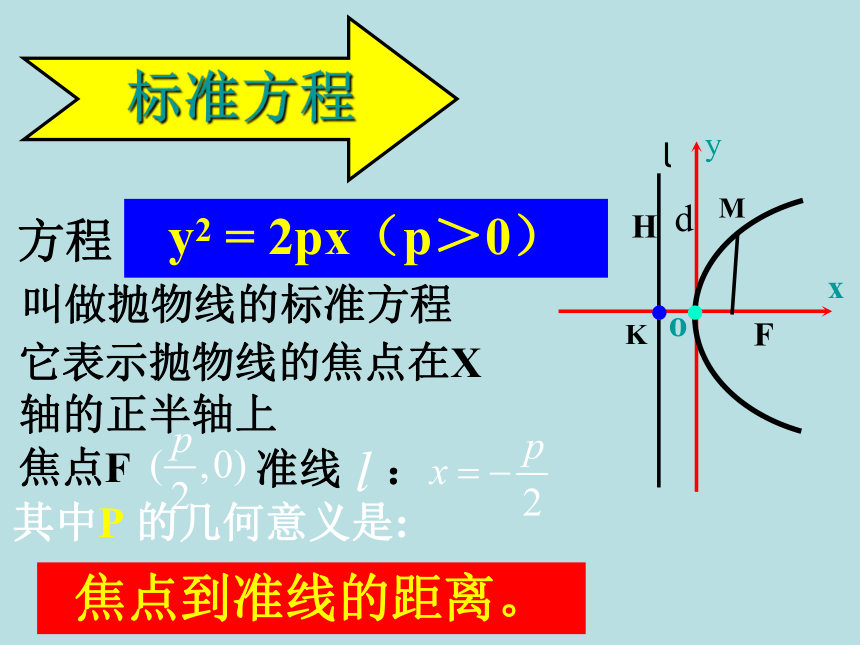
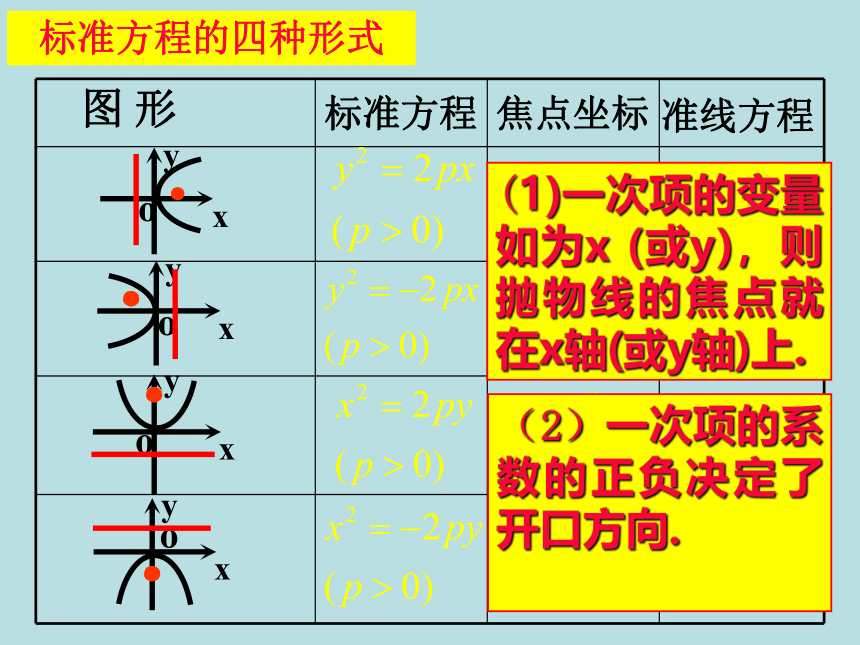
坐标系? 根据抛物线的几何特征,取经过点F且垂直于直线l的直线为x轴,垂足为K,并使原点与线段KF的中点重合.建立直角坐标系xoy。设︱KF︱= p (p>0),化简得 y2 = 2px(p>0)y2 = 2px(p>0)它表示抛物线的焦点在X轴的正半轴上 其中P 的几何意义是:焦点到准线的距离。探究:在建立椭圆、双曲线的标准方程时,选择不同的坐标系我们得到了不同形式的标准方程。那么,抛物线的标准方程有哪些不同的形式?标准方程的四种形式图 形准线方程焦点坐标标准方程(1)一次项的变量如为x (或y),则抛物线的焦点就在x轴(或y轴)上.(2)一次项的系数的正负决定了开口方向.
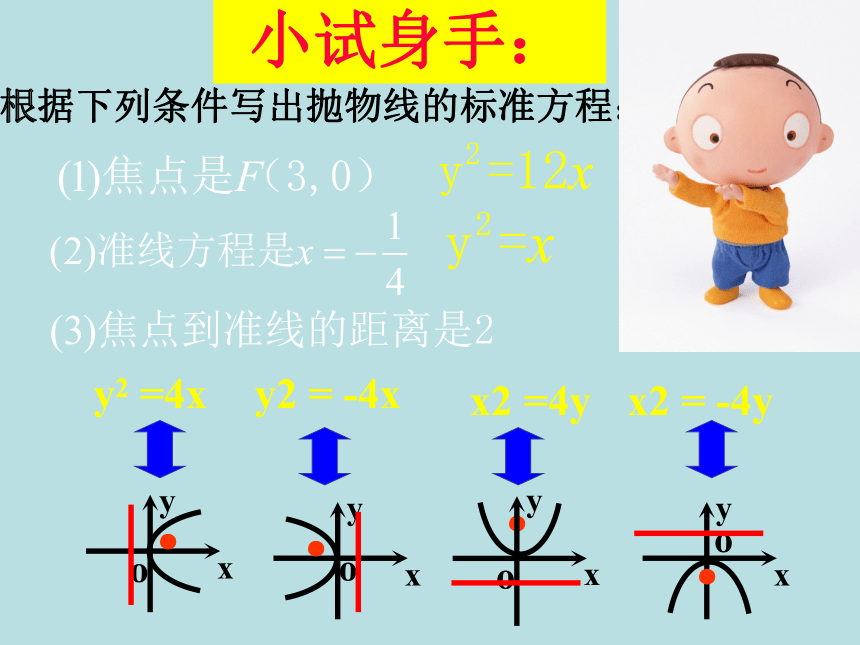
小试身手:根据下列条件写出抛物线的标准方程: 例1、(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;解:由方程知:p=3注:已知抛物线的标准方程,可求p,并能判断焦点位置,进而求焦点坐标或准线方程.例1、(2)已知抛物线的方程是y =- 6x2,
求它的焦点坐标和准线方程;解:原方程可化为:注:若已知的抛物线方程不是标准方程,要先转化为标准方程.求下列抛物线的焦点坐标和准线方程:练一练:(1)(2)(3)(4)方程准线方程焦点坐标思考:你能说明二次函数 的图象为什么是抛物线吗?指出它的焦点坐标、标准方程。例2、一种卫星接受天线的轴截面如图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接受天线,经反射聚集到焦点处,已知接收天线的口径(直径)为4.8m,深度为0.5m。试建立适当的坐标系,求抛物线的标准方程和焦点坐标例2、一种卫星接受天线的轴截面如图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接受天线,经反射聚集到焦点处,已知接收天线的口径(直径)为4.8m,深度为0.5m。试建立适当的坐标系,求抛物线的标准方程和焦点坐标即p=5.76解:如图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合。例2、一种卫星接受天线的轴截面如图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接受天线,经反射聚集到焦点处,已知接收天线的口径(直径)为4.8m,深度为0.5m。试建立适当的坐标系,求抛物线的标准方程和焦点坐标由已知条件可得,点A的坐标是(0.5,2.4),代入方程得填空:2、抛物线的标准方程、焦点、准线.小
结1、抛物线的定义. 3、抛物线标准方程的应用. 4、渗透了数形结合的重要思想.作 业 习题2.4
课本 P78: 1、2、3谢谢指导
思 考:如何建立适当的直角
坐标系? 根据抛物线的几何特征,取经过点F且垂直于直线l的直线为x轴,垂足为K,并使原点与线段KF的中点重合.建立直角坐标系xoy。设︱KF︱= p (p>0),化简得 y2 = 2px(p>0)y2 = 2px(p>0)它表示抛物线的焦点在X轴的正半轴上 其中P 的几何意义是:焦点到准线的距离。探究:在建立椭圆、双曲线的标准方程时,选择不同的坐标系我们得到了不同形式的标准方程。那么,抛物线的标准方程有哪些不同的形式?标准方程的四种形式图 形准线方程焦点坐标标准方程(1)一次项的变量如为x (或y),则抛物线的焦点就在x轴(或y轴)上.(2)一次项的系数的正负决定了开口方向.
小试身手:根据下列条件写出抛物线的标准方程: 例1、(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;解:由方程知:p=3注:已知抛物线的标准方程,可求p,并能判断焦点位置,进而求焦点坐标或准线方程.例1、(2)已知抛物线的方程是y =- 6x2,
求它的焦点坐标和准线方程;解:原方程可化为:注:若已知的抛物线方程不是标准方程,要先转化为标准方程.求下列抛物线的焦点坐标和准线方程:练一练:(1)(2)(3)(4)方程准线方程焦点坐标思考:你能说明二次函数 的图象为什么是抛物线吗?指出它的焦点坐标、标准方程。例2、一种卫星接受天线的轴截面如图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接受天线,经反射聚集到焦点处,已知接收天线的口径(直径)为4.8m,深度为0.5m。试建立适当的坐标系,求抛物线的标准方程和焦点坐标例2、一种卫星接受天线的轴截面如图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接受天线,经反射聚集到焦点处,已知接收天线的口径(直径)为4.8m,深度为0.5m。试建立适当的坐标系,求抛物线的标准方程和焦点坐标即p=5.76解:如图,在接收天线的轴截面所在平面内建立直角坐标系,使接收天线的顶点(即抛物线的顶点)与原点重合。例2、一种卫星接受天线的轴截面如图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接受天线,经反射聚集到焦点处,已知接收天线的口径(直径)为4.8m,深度为0.5m。试建立适当的坐标系,求抛物线的标准方程和焦点坐标由已知条件可得,点A的坐标是(0.5,2.4),代入方程得填空:2、抛物线的标准方程、焦点、准线.小
结1、抛物线的定义. 3、抛物线标准方程的应用. 4、渗透了数形结合的重要思想.作 业 习题2.4
课本 P78: 1、2、3谢谢指导
