2024-2025学年北师大版九年级数学下册课件2.2课时4 二次函数y=a(x-h)2+k的图像与性质
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册课件2.2课时4 二次函数y=a(x-h)2+k的图像与性质 |

|
|
| 格式 | pptx | ||
| 文件大小 | 404.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-19 17:17:18 | ||
图片预览


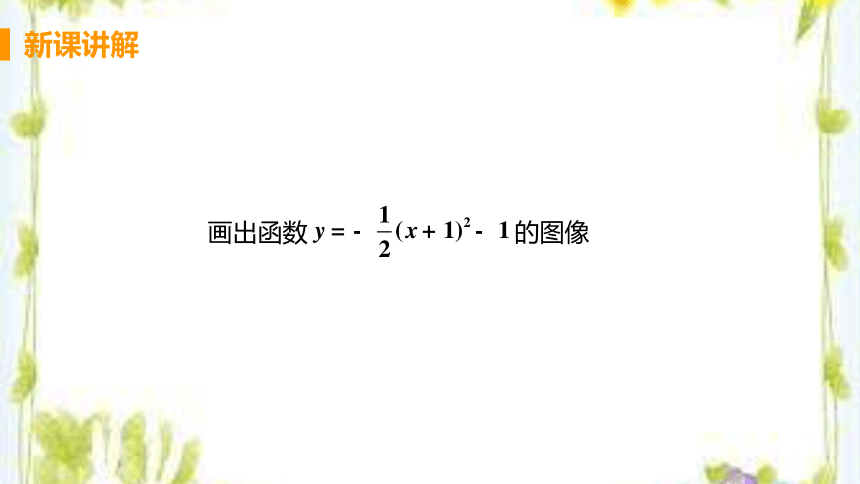







文档简介
(共31张PPT)
第二章 二次函数
2.2二次函数的图像和性质
课时4 二次函数y=a(x-h)2+k的图像与性质
1.二次函数y=a(x-h)2+k的图象(重点)
2.二次函数y=a(x-h)2+k的性质
3.二次函数y=a(x-h)2+k与y=ax2图象的平移关系
(重点、难点)
学习目标
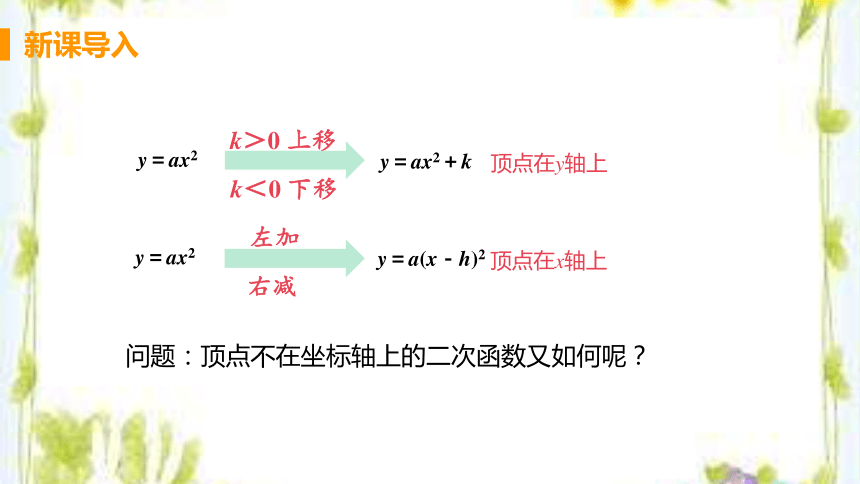
新课导入
y=ax2
k>0 上移
y=ax2+k
y=ax2
y=a(x-h)2
k<0 下移
顶点在y轴上
左加
右减
顶点在x轴上
问题:顶点不在坐标轴上的二次函数又如何呢?
新课讲解
画出函数 的图像
新课讲解
…
…
2
1
0
-1
-2
-3
-4
x
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
…
…
解: 先列表
再描点、连线
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
0
-1
-2
-3
-4
-5
-10
新课讲解
例
对于抛物线y=-(x+1)2+3,下列结论:
① 抛物线的开口向下;② 对称轴为直线x=1;
③ 顶点坐标为(-1,3);④ x>1 时,y 随x 的增大而减小.
其中正确结论有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
新课讲解
分析:①∵ a=-1<0,∴抛物线的开口向下,正确;
②对称轴为直线x=-1,错误;
③顶点坐标为(-1,3),正确;
④ x>1 时,y 随x 的增大而减小,正确.
综上所述,结论正确的是①③④,共3 个,故选C.
新课讲解
练一练
1.抛物线y=2(x-3)2+4的顶点坐标是( )
A.(3,4) B.(-3,4)
C.(3,-4) D.(2,4)
A
2.若抛物线y=(x-m)2+(m+1)的顶点在第一象
限,则m的取值范围为( )
A.m>1 B.m>0
C.m>-1 D.-1<m<0
B
新课讲解
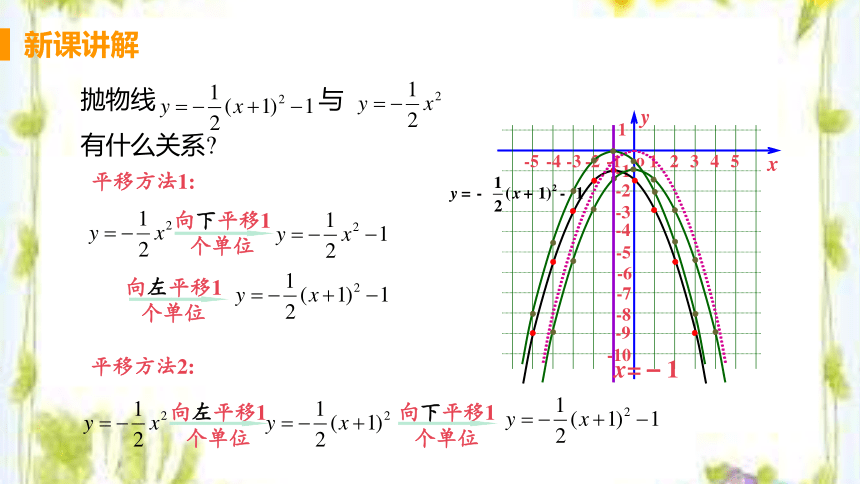
观察图象得到:抛物线的开口向下,
对称轴是直线x=-1,
顶点是(-1, -1).
抛物线 的开口方向、对称轴、顶点
新课讲解
向左平移1个单位
向下平移1个单位
向左平移1个单位
向下平移1个单位
平移方法1:
平移方法2:
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x=-1
抛物线 与
有什么关系
新课讲解
二次函数y=a(x-h)2+k与y=ax2图象有什么关系
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向左(右)平移,可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h,k的值来决定.
新课讲解
练一练
例
将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线对应的函数关系式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3
C.y=3(x+2)2-3 D.y=3(x-2)2-3
分析:由“上加下减”的原则可知,将抛物线y=3x2向上平移3个单位所得抛物线对应的函数关系式为y=3x2+3;由“左加右减”的原则可知,将抛物线y=3x2+3向左平移2个单位所得抛物线对应的函数关系式为y=3(x+2)2+3.
A
课堂小结
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上;
当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,k) .
当堂小练
1.二次函数y=a(x+m)2+n的图象如图所示,则一次函数y=mx+n的图象经过( )
A.第一、二、三象限
B.第一、二、四象限
C.第二、三、四象限
D.第一、三、四象限
C
当堂小练
2.将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线对应的函数表达式为( )
A.y=2x2+1
B.y=2x2-3
C.y=2(x-8)2+1
D.y=2(x-8)2-3
A
拓展与延伸
二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A. B.2 C. D.
D
分析:结合二次函数的增减性及图象的开口方向,对称轴进行解答即可.
1.
已知抛物线y=2(x-3)2,则:
(1)开口向 ;
(2)对称轴是 ;
(3)顶点坐标是 ;
(4)当x= 时,y的最 值是 ;
(5)当x 时,y随x的增大而增大.
>3
0
小
3
(3,0)
直线x=3
上
课后练习
2.(2024上海一模)将抛物线y=3x2向左平移2个单位长度,得到抛物线的表达式是( )
A.y=3x2-2 B.y=3x2+2
C.y=3(x-2)2 D.y=3(x+2)2
D
3.
已知抛物线y=-2(x-3)2-5,则:
(1)开口向 ;
(2)对称轴是 ;
(3)顶点坐标是 ;
(4)当x= 时,y的最 值是 ;
(5)当x 时,y随x的增大而减小.
>3
-5
大
3
(3,-5)
直线x=3
下
4.(2024广西)将抛物线y=x2先向右平移3个单位长度,再向上平移4个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+3)2-4
B.y=(x+3)2+4
C.y=(x-3)2+4
D.y=(x-3)2-4
C
x
y=-x2
y=-(x-1)2
函数 开口方向 对称轴 顶点坐标
y=-x2
y=-(x-1)2
y轴
(1,0)
(0,0)
直线x=1
向下
向下
5. (北师9下P38改编、人教9上P35改编)在同一个平面直角坐标系中,画出函数y=-x2与y=-(x-1)2的图象.
观察图象填空:
(填表画图略)
6.【例2】抛物线y=3(x-h)2向右平移3个单位长度后,得到抛物线y=3(x+2)2,则h= .
-5
7.如图,将抛物线y=x2向右平移a个单位长度后,顶点为A,与y轴交于点B,且△AOB为等腰直角三角形,求a的值.
解:平移后的抛物线的表达式为y=(x-a)2=x2-2ax+a2,∴顶点A的坐标为(a,0).
令x=0,则y=a2,∴B(0,a2).
∵△AOB为等腰直角三角形,
∴a=a2.解得a1=1,a2=0(舍去).
故a的值为1.
小结:用字母表示出关键点的坐标,列方程求解.
8.(2024杭州模拟)将抛物线y=2(x+3)2+1向左平移2个单位长度,再向下平移3个单位长度,则平移后抛物线的顶点坐标是( )
A.(5,-2) B.(1,-2)
C.(-1,4) D.(-5,-2)
D
小结:左右平移的规律——左“+”右“-”;
上下平移的规律——上“+”下“-”.
9.【例5】(2024广东)把抛物线y=2x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的表达式为
.
y=2(x+1)2-2
10.【例6】已知点(x1,y1),(x2,y2)在抛物线y=(x-h)2+k上,则:
(1)若x1<x2<h,则y1,y2,k的大小关系是 (用“<”连接);
(2)当x>3时,y随x的增大而增大,则h的取值范围为
.
h≤3
k<y2<y1
11.抛物线y=m(x+n)2向左平移2个单位长度后,得到抛物线y=-4(x-4)2,则m= ,n= .
-6
-4
★12. 0.50 (创新题)已知抛物线y=2(x-1)2的顶点为A,且与y轴交于点B.
(1)A的坐标为 ,B的坐标为 ;
(2)点P在抛物线上且在第一象限,S△PAB=2,求点P的坐标.
(0,2)
(1,0)
解:(2)∵y=2(x-1)2=2x2-4x+2,
∴设点P(a,2a2-4a+2),
如图,过点P作PC⊥x轴于点C,则S△PAB=S梯形PBOC-S△ABO-S△PAC=(2+2a2-4a+2)·a-1×2-(2a2-4a+2)×(a-1)=a2-a,∵S△PAB=2,∴a2-a=2.解得a1=-1(舍),a2=2.
∴点P的坐标为(2,2).
答案图
★13. 0.55 (创新题)(2023惠州月考)已知二次函数y=-(x-h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为-1,则h的值为( )
A.3或6 B.1或6
C.1或3 D.4或6
B
请完成课本本节对应习题
布置作业
感谢大家观看
第二章 二次函数
2.2二次函数的图像和性质
课时4 二次函数y=a(x-h)2+k的图像与性质
1.二次函数y=a(x-h)2+k的图象(重点)
2.二次函数y=a(x-h)2+k的性质
3.二次函数y=a(x-h)2+k与y=ax2图象的平移关系
(重点、难点)
学习目标
新课导入
y=ax2
k>0 上移
y=ax2+k
y=ax2
y=a(x-h)2
k<0 下移
顶点在y轴上
左加
右减
顶点在x轴上
问题:顶点不在坐标轴上的二次函数又如何呢?
新课讲解
画出函数 的图像
新课讲解
…
…
2
1
0
-1
-2
-3
-4
x
-5.5
-3
-1.5
-1
-1.5
-3
-5.5
…
…
解: 先列表
再描点、连线
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
0
-1
-2
-3
-4
-5
-10
新课讲解
例
对于抛物线y=-(x+1)2+3,下列结论:
① 抛物线的开口向下;② 对称轴为直线x=1;
③ 顶点坐标为(-1,3);④ x>1 时,y 随x 的增大而减小.
其中正确结论有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
新课讲解
分析:①∵ a=-1<0,∴抛物线的开口向下,正确;
②对称轴为直线x=-1,错误;
③顶点坐标为(-1,3),正确;
④ x>1 时,y 随x 的增大而减小,正确.
综上所述,结论正确的是①③④,共3 个,故选C.
新课讲解
练一练
1.抛物线y=2(x-3)2+4的顶点坐标是( )
A.(3,4) B.(-3,4)
C.(3,-4) D.(2,4)
A
2.若抛物线y=(x-m)2+(m+1)的顶点在第一象
限,则m的取值范围为( )
A.m>1 B.m>0
C.m>-1 D.-1<m<0
B
新课讲解
观察图象得到:抛物线的开口向下,
对称轴是直线x=-1,
顶点是(-1, -1).
抛物线 的开口方向、对称轴、顶点
新课讲解
向左平移1个单位
向下平移1个单位
向左平移1个单位
向下平移1个单位
平移方法1:
平移方法2:
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x=-1
抛物线 与
有什么关系
新课讲解
二次函数y=a(x-h)2+k与y=ax2图象有什么关系
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向左(右)平移,可以得到抛物线y=a(x-h)2+k.平移的方向、距离要根据h,k的值来决定.
新课讲解
练一练
例
将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线对应的函数关系式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3
C.y=3(x+2)2-3 D.y=3(x-2)2-3
分析:由“上加下减”的原则可知,将抛物线y=3x2向上平移3个单位所得抛物线对应的函数关系式为y=3x2+3;由“左加右减”的原则可知,将抛物线y=3x2+3向左平移2个单位所得抛物线对应的函数关系式为y=3(x+2)2+3.
A
课堂小结
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上;
当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,k) .
当堂小练
1.二次函数y=a(x+m)2+n的图象如图所示,则一次函数y=mx+n的图象经过( )
A.第一、二、三象限
B.第一、二、四象限
C.第二、三、四象限
D.第一、三、四象限
C
当堂小练
2.将抛物线y=2(x-4)2-1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线对应的函数表达式为( )
A.y=2x2+1
B.y=2x2-3
C.y=2(x-8)2+1
D.y=2(x-8)2-3
A
拓展与延伸
二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A. B.2 C. D.
D
分析:结合二次函数的增减性及图象的开口方向,对称轴进行解答即可.
1.
已知抛物线y=2(x-3)2,则:
(1)开口向 ;
(2)对称轴是 ;
(3)顶点坐标是 ;
(4)当x= 时,y的最 值是 ;
(5)当x 时,y随x的增大而增大.
>3
0
小
3
(3,0)
直线x=3
上
课后练习
2.(2024上海一模)将抛物线y=3x2向左平移2个单位长度,得到抛物线的表达式是( )
A.y=3x2-2 B.y=3x2+2
C.y=3(x-2)2 D.y=3(x+2)2
D
3.
已知抛物线y=-2(x-3)2-5,则:
(1)开口向 ;
(2)对称轴是 ;
(3)顶点坐标是 ;
(4)当x= 时,y的最 值是 ;
(5)当x 时,y随x的增大而减小.
>3
-5
大
3
(3,-5)
直线x=3
下
4.(2024广西)将抛物线y=x2先向右平移3个单位长度,再向上平移4个单位长度,得到的抛物线的函数表达式为( )
A.y=(x+3)2-4
B.y=(x+3)2+4
C.y=(x-3)2+4
D.y=(x-3)2-4
C
x
y=-x2
y=-(x-1)2
函数 开口方向 对称轴 顶点坐标
y=-x2
y=-(x-1)2
y轴
(1,0)
(0,0)
直线x=1
向下
向下
5. (北师9下P38改编、人教9上P35改编)在同一个平面直角坐标系中,画出函数y=-x2与y=-(x-1)2的图象.
观察图象填空:
(填表画图略)
6.【例2】抛物线y=3(x-h)2向右平移3个单位长度后,得到抛物线y=3(x+2)2,则h= .
-5
7.如图,将抛物线y=x2向右平移a个单位长度后,顶点为A,与y轴交于点B,且△AOB为等腰直角三角形,求a的值.
解:平移后的抛物线的表达式为y=(x-a)2=x2-2ax+a2,∴顶点A的坐标为(a,0).
令x=0,则y=a2,∴B(0,a2).
∵△AOB为等腰直角三角形,
∴a=a2.解得a1=1,a2=0(舍去).
故a的值为1.
小结:用字母表示出关键点的坐标,列方程求解.
8.(2024杭州模拟)将抛物线y=2(x+3)2+1向左平移2个单位长度,再向下平移3个单位长度,则平移后抛物线的顶点坐标是( )
A.(5,-2) B.(1,-2)
C.(-1,4) D.(-5,-2)
D
小结:左右平移的规律——左“+”右“-”;
上下平移的规律——上“+”下“-”.
9.【例5】(2024广东)把抛物线y=2x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的表达式为
.
y=2(x+1)2-2
10.【例6】已知点(x1,y1),(x2,y2)在抛物线y=(x-h)2+k上,则:
(1)若x1<x2<h,则y1,y2,k的大小关系是 (用“<”连接);
(2)当x>3时,y随x的增大而增大,则h的取值范围为
.
h≤3
k<y2<y1
11.抛物线y=m(x+n)2向左平移2个单位长度后,得到抛物线y=-4(x-4)2,则m= ,n= .
-6
-4
★12. 0.50 (创新题)已知抛物线y=2(x-1)2的顶点为A,且与y轴交于点B.
(1)A的坐标为 ,B的坐标为 ;
(2)点P在抛物线上且在第一象限,S△PAB=2,求点P的坐标.
(0,2)
(1,0)
解:(2)∵y=2(x-1)2=2x2-4x+2,
∴设点P(a,2a2-4a+2),
如图,过点P作PC⊥x轴于点C,则S△PAB=S梯形PBOC-S△ABO-S△PAC=(2+2a2-4a+2)·a-1×2-(2a2-4a+2)×(a-1)=a2-a,∵S△PAB=2,∴a2-a=2.解得a1=-1(舍),a2=2.
∴点P的坐标为(2,2).
答案图
★13. 0.55 (创新题)(2023惠州月考)已知二次函数y=-(x-h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为-1,则h的值为( )
A.3或6 B.1或6
C.1或3 D.4或6
B
请完成课本本节对应习题
布置作业
感谢大家观看
