北京课改版七年级上第四章简单的几何图形单元测试题含答案
文档属性
| 名称 | 北京课改版七年级上第四章简单的几何图形单元测试题含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 108.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-11 00:00:00 | ||
图片预览



文档简介
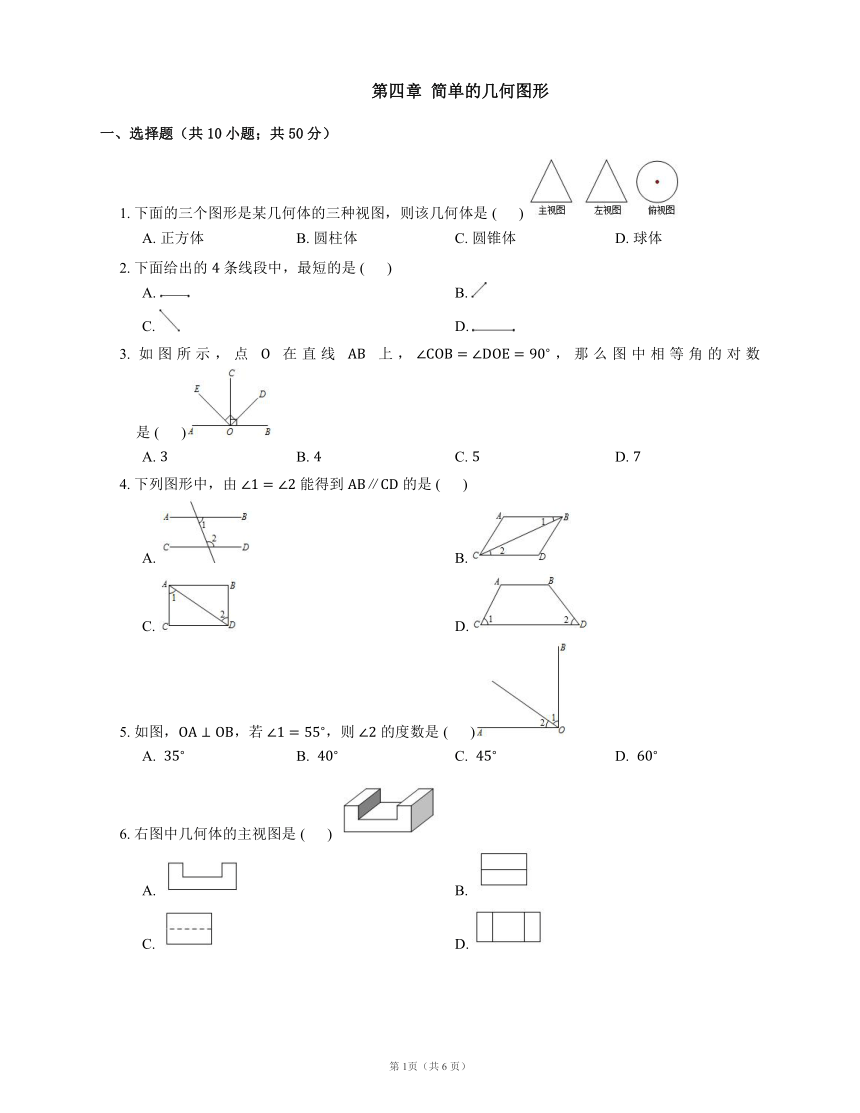
第四章 简单的几何图形
一、选择题(共10小题;共50分)
1. 下面的三个图形是某几何体的三种视图,则该几何体是 ( )
A. 正方体 B. 圆柱体 C. 圆锥体 D. 球体
2. 下面给出的 条线段中,最短的是 ( )
A. B.
C. D.
3. 如图所示,点 在直线 上,,那么图中相等角的对数是 ( )
A. B. C. D.
4. 下列图形中,由 能得到 的是 ( )
A. B.
C. D.
5. 如图,,若 ,则 的度数是 ( )
A. B. C. D.
6. 右图中几何体的主视图是 ( )
A. B.
C. D.
7. 如图所示是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是 到 .其中可看见 个面,其余 个面是看不见的,则看不见的面上的点数总和是 ( )
A. B. C. D.
8. 两条直线最多有 个交点,三条直线最多有 个交点,四条直线最多有 个交点,,那么六条直线最多有 ( )
A. 个交点 B. 个交点 C. 个交点 D. 个交点
9. 若一个棱柱有 个顶点,则在下列说法中,正确的是 ( )
A. 这个棱柱有 个侧面 B. 这个棱柱有 条侧棱
C. 这个棱柱的底面是六边形 D. 这个棱柱是一个十二棱柱
10. 江苏卫视智力问答节目《一站到底》深受广大电视爱好者喜欢,在某期节目中有这样一题:一副三角板不能拼出的角的度数是(拼接要求:既不重叠又不留空隙) ( )
A. B. C. D.
二、填空题(共10小题;共50分)
11. 你看这位""可爱吧!表面能展开平面图形""的是 .
12. 如图,请填写一个你认为恰当的条件 ,使 .
13. 一副三角板如图摆放,若 ,则 .
14. 一个正方体有 个面.
15. 在同一平面内,三条直线两两相交,最多有 个交点,那么 条直线两两相交,最多有 个交点, 条直线两两相交,最多有 个交点.
16. 如图是一个几何体的三视图,若这个几何体的体积是 ,则它的表面积是 .
17. 平面内不同的两点确定一条直线,不同的三点最多确定三条直线.若平面内的不同的 个点最多可确定 条直线,则 的值为 .
18. 填空:(1)如图所示,, 两点在线段 上,则 , ;(2)如果 ,,,那么 的长为 .
19. 如图,在 内以点 为端点的射线有 条,则图中共有 个角.
20. 在同一个学校上学的小明、小伟、小红三位同学住在 ,, 三个住宅区,如图所示,,, 三点共线,且 米, 米,他们打算合租一辆车接送上学,由于车位紧张,准备在此之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在 .
三、解答题(共6小题;共78分)
21. 把图中的图形与对应的图形名称用线连接起来.
22. 如图①所示,, 都是直角.
(1) 试猜想, 和 在数量上是否存在相等、互余或互补关系 你能说明你猜想的正确性吗
(2) 当 绕点 旋转到如图 ②所示的位置时,你的猜想还成立吗
23. 请根据图①②所示的数字,在图③中的空格中填上相应的数字.
24. 如图是一些小正方体搭成的几何体俯视图,小正方形中的数字表示该位置的小正方体的个数,请画出它的主视图,左视图.
25. 将下列各角用度、分、秒表示出来.
(1) ;
(2) ;
(3) .
26. 我们知道相交的两直线的交点个数是 ,记两平行直线的交点个数是 ;这样平面内的三条平行线它们的交点个数就是 ,经过同一点的三直线它们的交点个数就是 ;依次类推 .
(1) 请你画图说明同一平面内的五条直线最多有几个交点
(2) 平面内的五条直线可以有 个交点吗 如果有,请你画出符合条件的所有图形;如果没有,请说明理由.
(3) 在平面内画出 条直线,使交点个数恰好是 .
答案
第一部分
1. C 2. B 3. C 4. B 5. A
6. A 7. C 8. C 9. C 10. D
第二部分
11. 圆锥
12. 或 或 等(答案不唯一)
13.
14.
15. ;
16.
17.
18. ;;
19.
20. 处
第三部分
21. 如图.
22. (1) 与 互补.理由如下:
,,
即
所以 与 互补.
(2) 与 互补仍然成立.理由如下:
, 都是直角,
,
所以
即 与 互补.
23. 对面是 , 对面是 ( 在 与 之间), 对面是 .
24. 如图所示:
25. (1)
(2)
(3)
26. (1) 如图,最多有 个交点.
(2) 可以有 个交点,有 种不同的情形,如图.
(3) 在平面内画出 条直线,使交点个数恰好是 ,如图
第1页(共6 页)
一、选择题(共10小题;共50分)
1. 下面的三个图形是某几何体的三种视图,则该几何体是 ( )
A. 正方体 B. 圆柱体 C. 圆锥体 D. 球体
2. 下面给出的 条线段中,最短的是 ( )
A. B.
C. D.
3. 如图所示,点 在直线 上,,那么图中相等角的对数是 ( )
A. B. C. D.
4. 下列图形中,由 能得到 的是 ( )
A. B.
C. D.
5. 如图,,若 ,则 的度数是 ( )
A. B. C. D.
6. 右图中几何体的主视图是 ( )
A. B.
C. D.
7. 如图所示是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是 到 .其中可看见 个面,其余 个面是看不见的,则看不见的面上的点数总和是 ( )
A. B. C. D.
8. 两条直线最多有 个交点,三条直线最多有 个交点,四条直线最多有 个交点,,那么六条直线最多有 ( )
A. 个交点 B. 个交点 C. 个交点 D. 个交点
9. 若一个棱柱有 个顶点,则在下列说法中,正确的是 ( )
A. 这个棱柱有 个侧面 B. 这个棱柱有 条侧棱
C. 这个棱柱的底面是六边形 D. 这个棱柱是一个十二棱柱
10. 江苏卫视智力问答节目《一站到底》深受广大电视爱好者喜欢,在某期节目中有这样一题:一副三角板不能拼出的角的度数是(拼接要求:既不重叠又不留空隙) ( )
A. B. C. D.
二、填空题(共10小题;共50分)
11. 你看这位""可爱吧!表面能展开平面图形""的是 .
12. 如图,请填写一个你认为恰当的条件 ,使 .
13. 一副三角板如图摆放,若 ,则 .
14. 一个正方体有 个面.
15. 在同一平面内,三条直线两两相交,最多有 个交点,那么 条直线两两相交,最多有 个交点, 条直线两两相交,最多有 个交点.
16. 如图是一个几何体的三视图,若这个几何体的体积是 ,则它的表面积是 .
17. 平面内不同的两点确定一条直线,不同的三点最多确定三条直线.若平面内的不同的 个点最多可确定 条直线,则 的值为 .
18. 填空:(1)如图所示,, 两点在线段 上,则 , ;(2)如果 ,,,那么 的长为 .
19. 如图,在 内以点 为端点的射线有 条,则图中共有 个角.
20. 在同一个学校上学的小明、小伟、小红三位同学住在 ,, 三个住宅区,如图所示,,, 三点共线,且 米, 米,他们打算合租一辆车接送上学,由于车位紧张,准备在此之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在 .
三、解答题(共6小题;共78分)
21. 把图中的图形与对应的图形名称用线连接起来.
22. 如图①所示,, 都是直角.
(1) 试猜想, 和 在数量上是否存在相等、互余或互补关系 你能说明你猜想的正确性吗
(2) 当 绕点 旋转到如图 ②所示的位置时,你的猜想还成立吗
23. 请根据图①②所示的数字,在图③中的空格中填上相应的数字.
24. 如图是一些小正方体搭成的几何体俯视图,小正方形中的数字表示该位置的小正方体的个数,请画出它的主视图,左视图.
25. 将下列各角用度、分、秒表示出来.
(1) ;
(2) ;
(3) .
26. 我们知道相交的两直线的交点个数是 ,记两平行直线的交点个数是 ;这样平面内的三条平行线它们的交点个数就是 ,经过同一点的三直线它们的交点个数就是 ;依次类推 .
(1) 请你画图说明同一平面内的五条直线最多有几个交点
(2) 平面内的五条直线可以有 个交点吗 如果有,请你画出符合条件的所有图形;如果没有,请说明理由.
(3) 在平面内画出 条直线,使交点个数恰好是 .
答案
第一部分
1. C 2. B 3. C 4. B 5. A
6. A 7. C 8. C 9. C 10. D
第二部分
11. 圆锥
12. 或 或 等(答案不唯一)
13.
14.
15. ;
16.
17.
18. ;;
19.
20. 处
第三部分
21. 如图.
22. (1) 与 互补.理由如下:
,,
即
所以 与 互补.
(2) 与 互补仍然成立.理由如下:
, 都是直角,
,
所以
即 与 互补.
23. 对面是 , 对面是 ( 在 与 之间), 对面是 .
24. 如图所示:
25. (1)
(2)
(3)
26. (1) 如图,最多有 个交点.
(2) 可以有 个交点,有 种不同的情形,如图.
(3) 在平面内画出 条直线,使交点个数恰好是 ,如图
第1页(共6 页)
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
