人教版数学八上课件14.1.1同底数幂的乘法(共17张PPT)
文档属性
| 名称 | 人教版数学八上课件14.1.1同底数幂的乘法(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 73.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-12 21:16:34 | ||
图片预览





文档简介
课件17张PPT。14.1.1同底数幂的乘法一、教学目标1.进一步体会幂的意义;
2.理解同底数幂的乘法法则及其推导过程;
3.能熟练运用同底数幂的乘法法则进行计算;
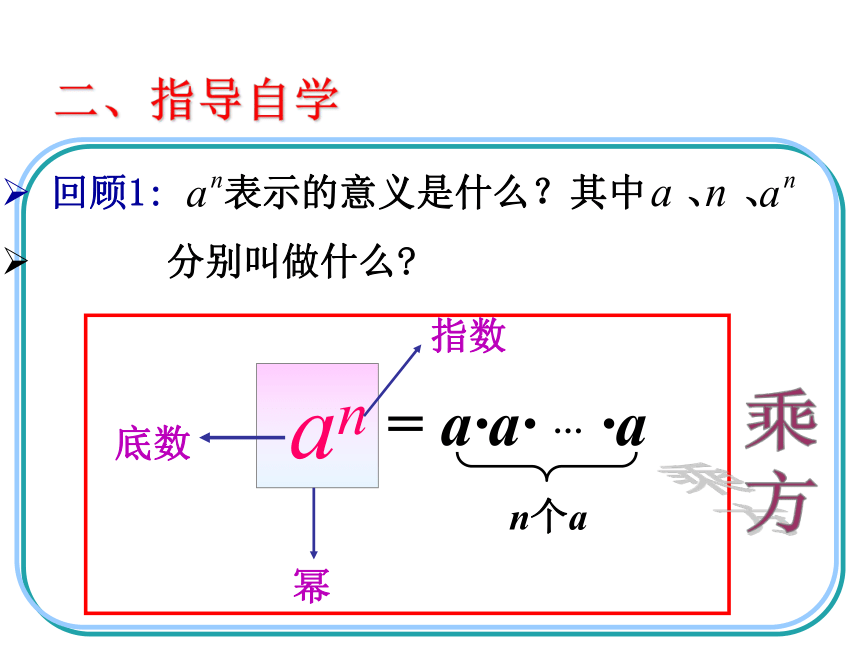
4.能运用同底数幂的乘法法则解决一些实际问题。二、指导自学 回顾1: 表示的意义是什么?其中 、 、
分别叫做什么? an底数幂指数乘
方二、指导自学 回顾2:(1) 表示什么?
(2) 改写成乘方的形式.解:(1)(2)二、指导自学问题1:一种电子计算机每秒可进行 次运算,
它工作 秒可进行多少次运算?解:二、指导自学问题2:根据乘方的意义填空,观察计算的结果有什么规律? ( ) ( )
( ) ( )
(3) ( ) ( )
77个2个2( )m+n思考:观察上面各题左右两边,底数、指数有 什么关系?你能得到什么结论?
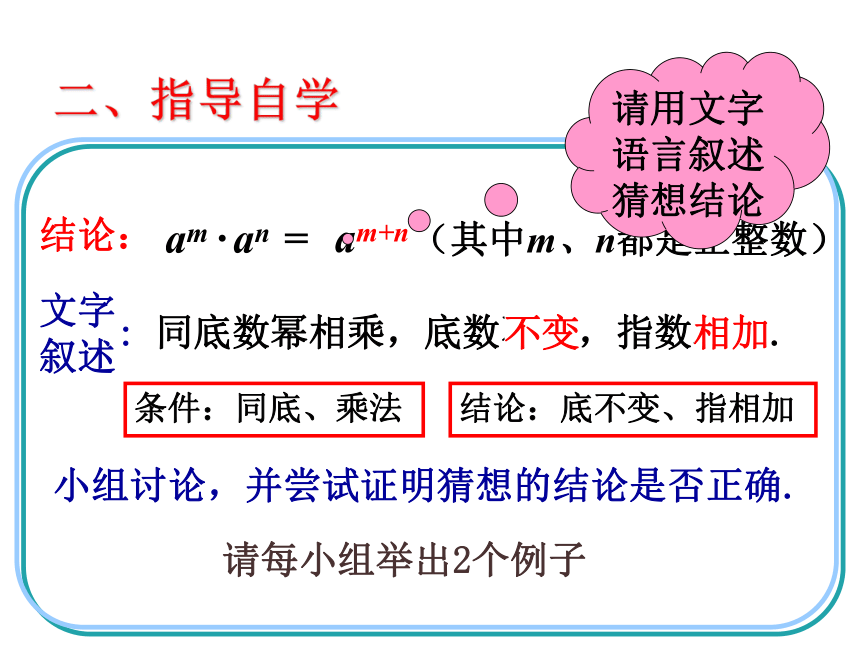
相乘结果底数与原底数 相同 ,指数是原来两个幂指数的 和 . 二、指导自学小组讨论,并尝试证明猜想的结论是否正确. am · an = ? (其中m、n都是正整数)猜想: : 同底数幂相乘,底数不变,指数相加.文字
叙述 am+n 结论:请用文字语言叙述猜想结论不变相加请每小组举出2个例子条件:同底、乘法结论:底不变、指相加二、指导自学想一想:当三个或三个以上同底数幂相乘时,
是否也具有这一性质呢? 怎样用公式表示?其中(m、n、p都是正整数)三、应用提高例1.计算下列各式,结果用幂的形式表示. x2 · x5 ; (2) a · a6 ;
(3) 2× 24× 23 ; (4) xm · x3m+1 ; 三、应用提高例3.计算:三、应用提高解: 例4.若am+n=6,an=3,求:am 的值.三、应用提高四、当堂训练(一)基础练习1.下面的计算对不对?如果不对,怎样改正?× √ × × ( )( )( )( )四、当堂训练(一)基础练习2.填空:
(1) ( )
3(2) ( ) (3) ,则 ;(4) ,则6四、当堂训练(一)基础练习四、当堂训练(二)拓展提高五、课堂小结我学到了什么?知识方法同底数幂相乘,底数不变,指数相加.
(m、n正整数)特殊→一般→特殊 灵活应用公式,注意公式的正用、逆用、变形用.
2.理解同底数幂的乘法法则及其推导过程;
3.能熟练运用同底数幂的乘法法则进行计算;
4.能运用同底数幂的乘法法则解决一些实际问题。二、指导自学 回顾1: 表示的意义是什么?其中 、 、
分别叫做什么? an底数幂指数乘
方二、指导自学 回顾2:(1) 表示什么?
(2) 改写成乘方的形式.解:(1)(2)二、指导自学问题1:一种电子计算机每秒可进行 次运算,
它工作 秒可进行多少次运算?解:二、指导自学问题2:根据乘方的意义填空,观察计算的结果有什么规律? ( ) ( )
( ) ( )
(3) ( ) ( )
77个2个2( )m+n思考:观察上面各题左右两边,底数、指数有 什么关系?你能得到什么结论?
相乘结果底数与原底数 相同 ,指数是原来两个幂指数的 和 . 二、指导自学小组讨论,并尝试证明猜想的结论是否正确. am · an = ? (其中m、n都是正整数)猜想: : 同底数幂相乘,底数不变,指数相加.文字
叙述 am+n 结论:请用文字语言叙述猜想结论不变相加请每小组举出2个例子条件:同底、乘法结论:底不变、指相加二、指导自学想一想:当三个或三个以上同底数幂相乘时,
是否也具有这一性质呢? 怎样用公式表示?其中(m、n、p都是正整数)三、应用提高例1.计算下列各式,结果用幂的形式表示. x2 · x5 ; (2) a · a6 ;
(3) 2× 24× 23 ; (4) xm · x3m+1 ; 三、应用提高例3.计算:三、应用提高解: 例4.若am+n=6,an=3,求:am 的值.三、应用提高四、当堂训练(一)基础练习1.下面的计算对不对?如果不对,怎样改正?× √ × × ( )( )( )( )四、当堂训练(一)基础练习2.填空:
(1) ( )
3(2) ( ) (3) ,则 ;(4) ,则6四、当堂训练(一)基础练习四、当堂训练(二)拓展提高五、课堂小结我学到了什么?知识方法同底数幂相乘,底数不变,指数相加.
(m、n正整数)特殊→一般→特殊 灵活应用公式,注意公式的正用、逆用、变形用.
