人教版数学九上课件 24.4.1 弧长和扇形面积(共19张PPT)
文档属性
| 名称 | 人教版数学九上课件 24.4.1 弧长和扇形面积(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 269.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-12 00:00:00 | ||
图片预览



文档简介
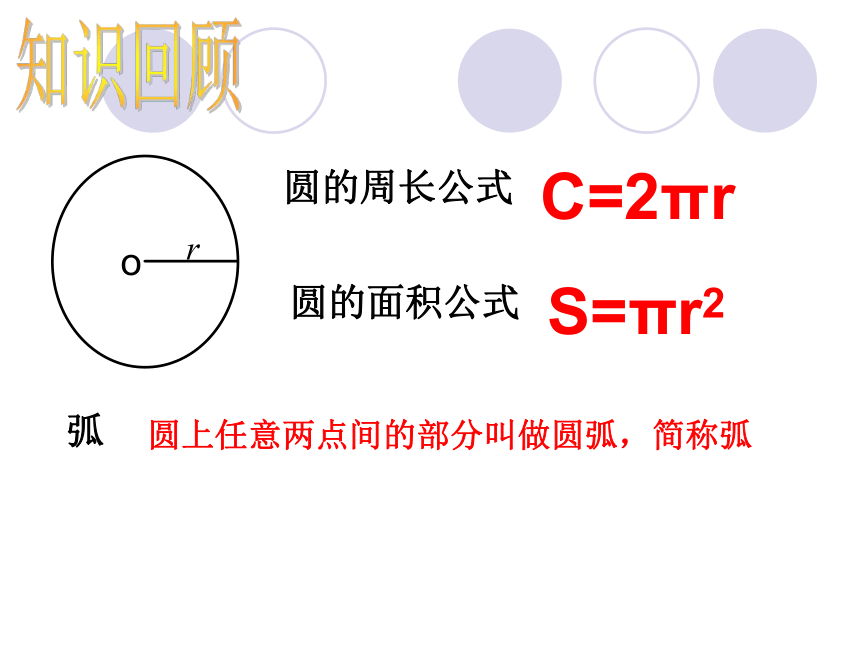
课件19张PPT。24.4.1 弧长和扇形面积漆 艳o圆的周长公式圆的面积公式C=2πrS=πr2弧圆上任意两点间的部分叫做圆弧,简称弧知识回顾
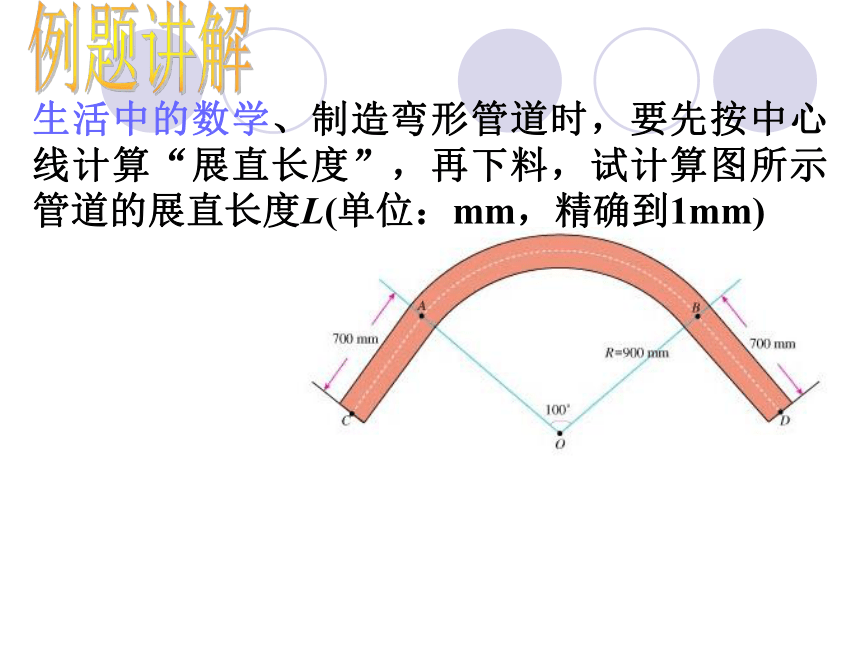
生活中的数学、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
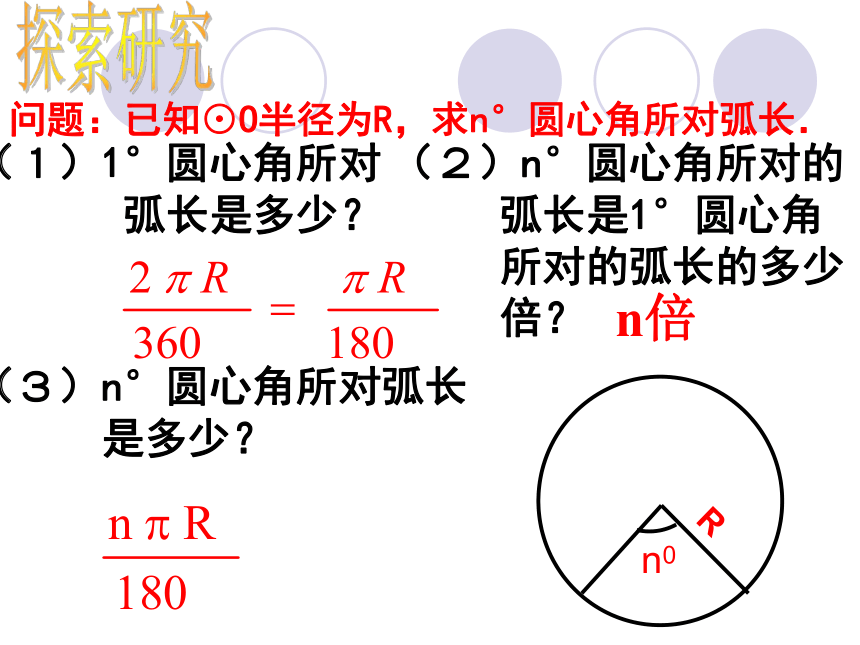
例题讲解问题:已知⊙O半径为R,求n°圆心角所对弧长.(1)1°圆心角所对
弧长是多少? (2)n°圆心角所对的
弧长是1°圆心角
所对的弧长的多少
倍? n倍(3)n°圆心角所对弧长
是多少? 探索研究 若设⊙O半径为R, n°的圆心角所对的弧长为L,则 (1)在应用弧长公式L 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.弧长公式
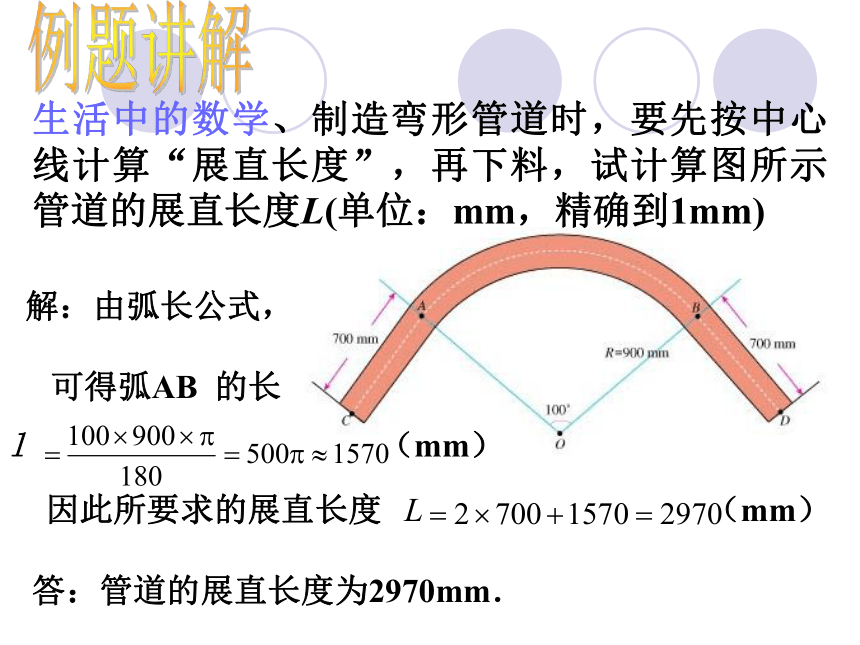
生活中的数学、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,
可得弧AB 的长
l (mm) 因此所要求的展直长度 L (mm) 答:管道的展直长度为2970mm. 例题讲解 在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有多大?
(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?问题探究 Πr2=25 Π
扇形的定义由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.图中阴影部分的图形叫什么呢?扇形新知探究 已知⊙O半径为R,求圆心角n°的扇形的面积? (1)圆面积可以看作是多少度的圆心角所对的 扇形的面积? 360°(2)圆心角为1°的扇形的面积是多少? (3)圆心角为n°的扇形的面积是圆心角为
1°的扇形的面积的多少倍? n倍 (4)圆心角为n°的扇形的面积是多少? 探索研究 若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形=
注意:
在应用扇形的面积公式S扇形=
进行计算时,要注意公式中n的意义.
n表示1°圆心角的倍数,它是不带单位的
扇形面积 在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有大?
(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?问题探究 Πr2=25 Π比较弧长公式与扇形面积公式l 弧S扇形在这两个公式中,弧长和扇形面积都和圆心角n°、半径R有关系,因此l 和S之间也有一定的关系,你能猜得出吗? 例:如图、水平放置的圆柱形排水管道的截面半径是1m,其中水面高0.5m,求截面上有水部分的面积。CD例题讲解2、已知半径为2的扇形,面积为 ,
则它的圆心角的度数为___.
3、已知半径为2的扇形,面积为 ,
则这个扇形的弧长=____.10∏120°小试牛刀1、已知圆弧的半径为30厘米,圆心
角为60°,则此圆弧的长度为___
4.如图所示,把边长为2的正方形ABCD的一边放在定直线L上,按顺时针方向绕点D旋转到如图的位置,则点B运动到点B′所经过的路线长度为 ________ 一、弧长的计算公式二、扇形面积计算公式课堂小结这节课你有什么收获?
1.如图,A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于 。拓展提高2.如图,已知P、Q分别是半径为1的半圆圆周上的两个三等分点,AB是直径,则阴影部分的面积等于 。拓展提高作业课本 P115页 5、6、7
生活中的数学、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
例题讲解问题:已知⊙O半径为R,求n°圆心角所对弧长.(1)1°圆心角所对
弧长是多少? (2)n°圆心角所对的
弧长是1°圆心角
所对的弧长的多少
倍? n倍(3)n°圆心角所对弧长
是多少? 探索研究 若设⊙O半径为R, n°的圆心角所对的弧长为L,则 (1)在应用弧长公式L 进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.弧长公式
生活中的数学、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,
可得弧AB 的长
l (mm) 因此所要求的展直长度 L (mm) 答:管道的展直长度为2970mm. 例题讲解 在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有多大?
(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?问题探究 Πr2=25 Π
扇形的定义由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.图中阴影部分的图形叫什么呢?扇形新知探究 已知⊙O半径为R,求圆心角n°的扇形的面积? (1)圆面积可以看作是多少度的圆心角所对的 扇形的面积? 360°(2)圆心角为1°的扇形的面积是多少? (3)圆心角为n°的扇形的面积是圆心角为
1°的扇形的面积的多少倍? n倍 (4)圆心角为n°的扇形的面积是多少? 探索研究 若设⊙O半径为R,圆心角为n°的扇形的面积
S扇形=
注意:
在应用扇形的面积公式S扇形=
进行计算时,要注意公式中n的意义.
n表示1°圆心角的倍数,它是不带单位的
扇形面积 在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:(1)这头牛吃草的最大活动区域有大?
(2)如果这头牛只能绕柱子转过80°角,那么它的最大活动区域有多大?问题探究 Πr2=25 Π比较弧长公式与扇形面积公式l 弧S扇形在这两个公式中,弧长和扇形面积都和圆心角n°、半径R有关系,因此l 和S之间也有一定的关系,你能猜得出吗? 例:如图、水平放置的圆柱形排水管道的截面半径是1m,其中水面高0.5m,求截面上有水部分的面积。CD例题讲解2、已知半径为2的扇形,面积为 ,
则它的圆心角的度数为___.
3、已知半径为2的扇形,面积为 ,
则这个扇形的弧长=____.10∏120°小试牛刀1、已知圆弧的半径为30厘米,圆心
角为60°,则此圆弧的长度为___
4.如图所示,把边长为2的正方形ABCD的一边放在定直线L上,按顺时针方向绕点D旋转到如图的位置,则点B运动到点B′所经过的路线长度为 ________ 一、弧长的计算公式二、扇形面积计算公式课堂小结这节课你有什么收获?
1.如图,A是半径为1的圆O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于 。拓展提高2.如图,已知P、Q分别是半径为1的半圆圆周上的两个三等分点,AB是直径,则阴影部分的面积等于 。拓展提高作业课本 P115页 5、6、7
同课章节目录
