2025年中考数学真题考点过关练--第7关 一元二次方程(含答案)
文档属性
| 名称 | 2025年中考数学真题考点过关练--第7关 一元二次方程(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 69.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 11:01:05 | ||
图片预览




文档简介
第7关 一元二次方程
基础练
考点 1 一元二次方程及其解法
1.「2024四川凉山州1若关于x的一元二次方程 的一个根是x=0、则a的值为 ( )
A.2 B.-2 C.2或-2 D.
2.[2024 贵州`一元二次方程 的解是( )
3.2024 内蒙古赤峰]等腰三角形的两边长分别是方程 的两个根,则这个三角形的周长为 ( )
A.17或13 B.13 或21
C.17 D.13
考点 2 根的判别式、根与系数的关系
4.2024 北京若关于x的一元二次方程 =0有两个相等的实数根,则实数c的值为( )
A.-16 B.-4 C.4 D.16
5.[2024四川自贡]关于x的方程 根的情况是 ( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
6.[2024四川乐山]若关于x的一元二次方程x +2x+p=0两根为x ,x ,且 则p的值为( )
B. C.-6 D.6
7.[2024 北京西城区二模]已知关于x的一元二次方程 有两个不相等的实数根.
(1)求实数k的取值范围;
(2)若k为满足条件的最大整数,求此时方程的根.
考点 3 一元二次方程的实际应用
8.[2024云南]两年前生产1千克甲种药品的成本为80元,随着生产技术的进步,现在生产1千克甲种药品的成本为60元.设甲种药品成本的年平均下降率为x,根据题意,下列方程正确的是 ( )
C.80(1-x)=60 D.80(1-2x)=60
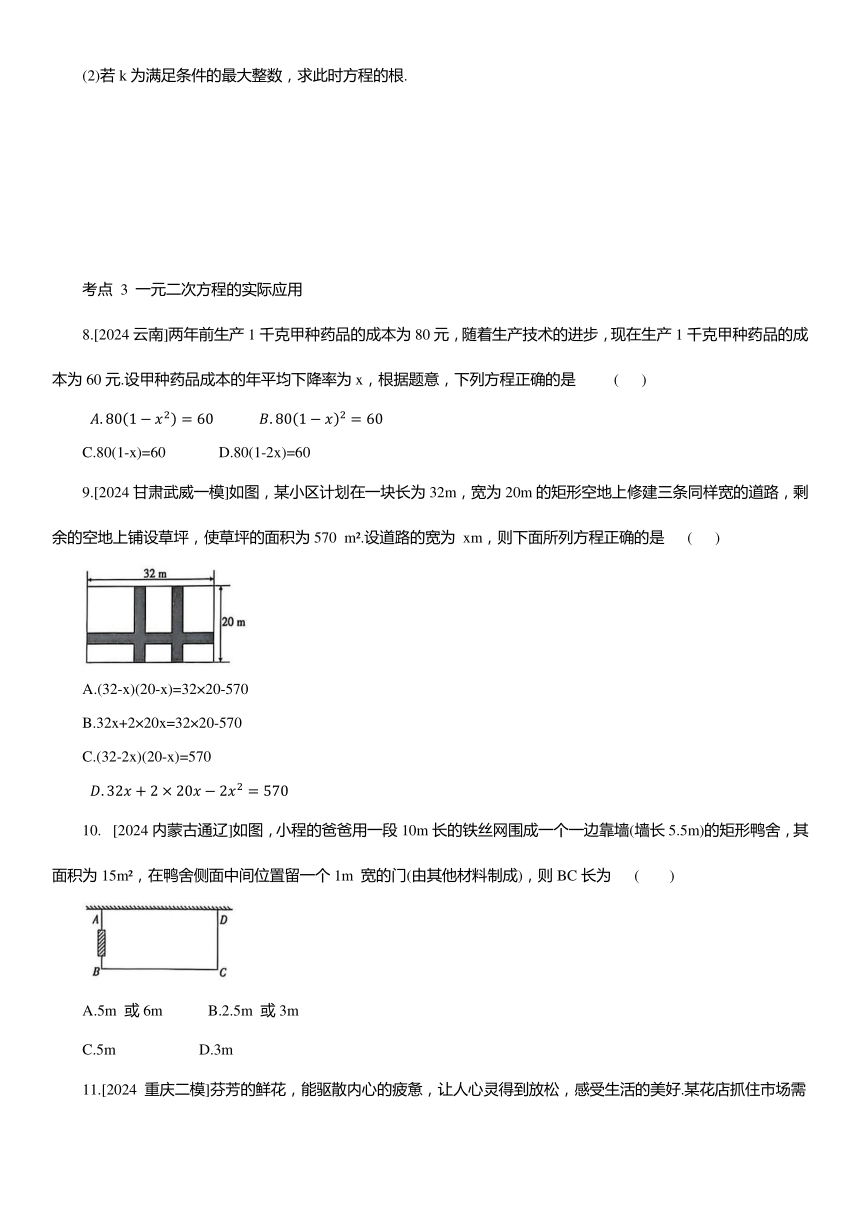
9.[2024甘肃武威一模]如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上铺设草坪,使草坪的面积为570 m .设道路的宽为 xm,则下面所列方程正确的是 ( )
A.(32-x)(20-x)=32×20-570
B.32x+2×20x=32×20-570
C.(32-2x)(20-x)=570
[2024内蒙古通辽]如图,小程的爸爸用一段10m长的铁丝网围成一个一边靠墙(墙长5.5m)的矩形鸭舍,其面积为15m ,在鸭舍侧面中间位置留一个1m 宽的门(由其他材料制成),则BC长为 ( )
A.5m 或6m B.2.5m 或3m
C.5m D.3m
11.[2024 重庆二模]芬芳的鲜花,能驱散内心的疲惫,让人心灵得到放松,感受生活的美好.某花店抓住市场需求,计划第一次购进玫瑰和向日葵共300枝,每枝玫瑰的进价为2元,售价定为5元,每枝向日葵的进价为4元,售价定为10元.
(1)若花店在无损耗的情况下将玫瑰和向日葵全部售完,要求总获利不低于1 200元,求花店最多购进玫瑰多少枝.
(2)花店在第二次购进玫瑰和向日葵时,两种花的进价不变.由于销售火爆,花店决定购进玫瑰和向日葵共360枝,其中玫瑰的进货量在
(1)的最多进货量的基础上增加10m枝,售价比第一次提高m元,向日葵售价不变,但向日葵在运输过程中有10%已经损坏,无法进行销售,最终第二批花全部售完后销售利润为1800元,求m的值.
提升练
12.[2024辽宁丹东校级模拟]下列方程是关于x的一元二次方程的是 ( )
13.[2024黑龙江绥化]小影与小冬一起写作业,在解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是-2和-5,则原来的方程是 ( )
14.[2024 广东深圳三模]“指尖上的非遗———麻柳刺绣”,针线勾勒之间,绣出世间百态.在一幅长80 cm,宽50cm 的刺绣风景画的四周镶一圈金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5 400 cm ,设金色纸边的宽度为x cm(风景画四周的金色纸边宽度相同),则列出的方程为 ( )
A.(50+x)(80+x)=5400
B.(50-x)(80-x)=5400
C.(50+2x)(80+2x)=5400
D.(50-2x)(80-2x)=5400
15.[2024四川南充一模]关于x的方程 的两个根x ,x 满足 且x >x ,则m的值为 ( )
A.-3 B.1
C.3 D.9
16.[2024江苏扬州校级模拟]根据下表可知,方程 的一个解x的范围为 ( )
x 0.28 0.29 0.30 0.31 0.32
y=x + 3x-1 -0.0816 -0.0459 -0.01 0.0261 0.0624
A.0.28C.0.3017.[2024云南]若一元二次方程 无实数根,则实数c的取值范围为 .
18.[2024四川南充]已知m 是方程 的一个根,则(m+5)(m-1)的值为 .
19.[2024江苏靖江二模]若 4y·+3、则M 的最小值为 .
20.[2024 重庆B卷]重庆在低空经济领域实现了新的突破、今年第一季度低空飞行航线安全运行了200架次,预计第三季度低空飞行航线安全运行将达到401 架次.设第二、第三两个季度安全运行架次的平均增长率为x,根据题意,可列方程为 .
21.2024 重庆A卷]随着经济复苏,某公司近两年的总收入逐年递增.该公司2021年缴税40万元,2023年缴税48.4 万元.该公司这两年缴税的年平均增长率是 .
22.2024 青海 (1)解一元二次方程:
(2)若直角三角形的两边长分别是(1)中方程的根,求第三边的长.
23.[2024浙江舟山二模]小敏与小霞两位同学解方程 的过程如下:
小敏: 两边同除以(x-3),得3=x-3, 则x=6.
小霞: 移项,得:3(x-3)-(x-3) =0, 提取公因式,得(x-3)(3-x-3)=0, 则x-3=0或3-x-3=0, 解得x =3,x =0.
你认为她们的解法是否正确 若正确,请在框内打“ ”;若错误,请在框内打“×”,并写出你的解答过程.
24.[2024广东广州]关于x的方程 有两个不等的实数根.
(1)求m的取值范围;
(2)化简:
25.[2024四川内江]已知关于x的一元二次方程 (p为常数)有两个不相等的实数根x 和x .
(1)填空:
(2)求
(3)已知 求p的值.
26.[2024 辽宁一模]某校乒乓球队举行队内比赛,比赛规则是每两个队员之间都比赛一场,每场比赛都要分出胜负,每一场比赛结束后依据胜负获得相应积分,本次比赛一共进行了210场,用时两天完成,下面是第一天比赛结束后部分队员的积分表:
队员号码 比赛场次 胜场 负场 积分
1 10 8 2 18
2 10 10 0 20
3 8 7 1 15
4 8 6 2 14
5 7 0 7 7
(1)在本次比赛中,有一名队员只输掉了一场比赛,则该名队员的积分是多少
(2)如果有一名队员在本次比赛中的积分不低于34分,那么他最多负 场.
27.[2024甘肃兰州校级模拟]如图,A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点 P,Q分别从点A,C 同时出发,点 P 以 3c m/s的速度向点 B 移动,到达 B 点时停止,点Q 以2cm /s的速度向 D 点移动,当点 P 到达 B 点时点 Q 随之停止运动.设运动时间为 ts.
(1)AP = ,BP = ,CQ = ,DQ= (用含 t 的代数式表示);
(2)t为多少时,四边形 PBCQ 的面积为33cm
(3)t为多少时,点 P 和点 Q 的距离为10 cm
第7关 一元二次方程
1. A 解析:∵关于x的一元二次方程(a+ 的一个根是x=0, 且a+2≠0,解得(a=2.
2. B 解析: x(x-2)=0,x-2=0或x=0,
解得
3C 解析:
(x-3)(x-7)=0,
解得
当等腰三角形的边长是3、3、7时,3+3<7、不符合三角形的三边关系,舍去;
当等腰三角形的边长是7、7、3时,这个三角形的周长是7+7+3=17.
4. C 解析:∵方程 有两个相等的实数根,
∴4c=16,解得c=4.
5. A 解析:关于x的方程. 中,∵a=1,b=m,c=-2,
∴方程有两个不相等的实数根.
6. A 解析:∵关于x的一元二次方程. 2x+p=0两根为x ,x ,
則
7.(1)k< (2)x =-1,x =-2
解析:(1)由题意可知 17-4k>0,解得
(2)由(1)可知k=4,
∴此时方程为
∴(x+1)(x+2)=0,
8. B
9. C 解析:∵道路的宽为 xm,
∴铺设草坪的部分可合成长为(32-2x)m,宽为(20-x)m的矩形.
根据题意得(32-2x)(20-x)=570.
10. C 解析:设BC长为 xm,则AB的长为
根据题意得·
解得x=5或x=6(舍去).
故BC长为5m.
11.(1)200枝(2)m=2
解析:(1)设花店购进玫瑰x枝,则购进向日葵(300-x)枝,
根据题意得(5-2)x+(10-4)(300-x)
≥1200,
解得x≤200,
∴x的最大值为200.
答:花店最多购进玫瑰200枝.
(2)根据题意得((5+m)(200+10m)-2(200+10m)+10[360-(200+10m)]×(1-10%)-4[360-(200+10m)]=1800,
整理得
解得 (不符合题意,舍去).
答:m的值为2.
12. D 解析:A.当a=0时, 不是一元二次方程,故A 不符合题意;
不是整式方程,故B不符合题意;
是一元一次方程,故C不符合题意;
是一元二次方程,故D符合题意.
故选 D.
13. B 解析:设原来的方程为 (a≠0),
则
所以b=-7a,c=10a,
所以原来的方程为 即
14. C 解析:由题意得挂图的长为(80+2x) cm,宽为(50+2x) cm,根据题意得(50+2x)(80+2x)=5400.
15. C 解析:∵
∴(x-m+2)(x-m-2)=0,
∴x-m+2=0或x-m-2=0,
∴m+2=2(m-2)+3,
解得m=3.
故选C.
16. C 解析:∵当x=0.30时, -0.01<0,
当x=0.31|时,
∴方程 的一个解x的范围为0.3017. c>1
解析:因为一元二次方程 无实数根,所以. 解得c>1.
18.-4
解析:∵m是方程. 的一个根,
19.2
解析:/ 故答案为2.
21.10%
解析:设年平均增长率是x,
则有
解得x=0.1=10%或x=-2.1(舍).
22.(1)x =1,x =3 (2)2 或
解析:
∴(x-1)(x-3)=0.
∴x-1=0或x-3=0,
(2)当3是直角三角形的斜边长时,第三边的长
当1和3是直角三角形的两直角边长时,第三边的长:
∴第三边的长为2 或
23.都错误,两框内均打“×”,解答过程见解析
解析:移项,得
提取公因式,得((x-3)(3-x+3)=0,
则x-3=0或:3-x+3=0,
解得
24.(1)m>3 (2)-2
解析:(1)∵关于x的方程 =0有两个不等的实数根,
解得m>3.
(2)∵m>3,
=-2.
25.(1)p;1
(3)p=3
解析:(1)由根与系数的关系得
∵关于x的一元二次方程 (p为常数)有两个不相等的实数根x 和
即
解得
当.p=3时,
当p=-1时 舍去.
∴p=3.
26.(1)39分 (2)6
解析:(1)设共有x个队员参加比赛,由题表得赢一场比赛得 20÷10=2(分),输掉一场比赛得7÷7=1(分),由题意得 解得x=21(负值舍去),
∴共有21个队员参加比赛,
∴每个队员一共比赛20场,(20-1)×2+1=39(分).
答:该名队员的积分是39分.
(2)设该名队员在本次比赛中负y场,由题意得(20-y)×2+y≥34,解得y≤6,
∴该名队员在本次比赛中最多负6场,故答案为6.
27.(1)3t cm;(16-3t) cm;2t cm;(16-2t) cm (2)t=5 (3) 或
解析:(1)当运动时间为 ts 时,AP=3t cm,BP=(16-3t) cm,CQ=2t cm,DQ=(16-2t) cm.
故答案为3t cm;(16-3t) cm;2t cm;(16-2t) cm.
(2)依题意得- 整理得16-t=11,
解得t=5.
答:当t为5时,四边形 PBCQ 的面积为33cm .
(3)过点 Q 作 QE⊥AB 于点 E,则 PE=|(16-3t)-2t|=|16-5t|.
依题意得|
即
解得
答:当t为 或 时,点P 和点 Q 的距离为10 cm.
基础练
考点 1 一元二次方程及其解法
1.「2024四川凉山州1若关于x的一元二次方程 的一个根是x=0、则a的值为 ( )
A.2 B.-2 C.2或-2 D.
2.[2024 贵州`一元二次方程 的解是( )
3.2024 内蒙古赤峰]等腰三角形的两边长分别是方程 的两个根,则这个三角形的周长为 ( )
A.17或13 B.13 或21
C.17 D.13
考点 2 根的判别式、根与系数的关系
4.2024 北京若关于x的一元二次方程 =0有两个相等的实数根,则实数c的值为( )
A.-16 B.-4 C.4 D.16
5.[2024四川自贡]关于x的方程 根的情况是 ( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
6.[2024四川乐山]若关于x的一元二次方程x +2x+p=0两根为x ,x ,且 则p的值为( )
B. C.-6 D.6
7.[2024 北京西城区二模]已知关于x的一元二次方程 有两个不相等的实数根.
(1)求实数k的取值范围;
(2)若k为满足条件的最大整数,求此时方程的根.
考点 3 一元二次方程的实际应用
8.[2024云南]两年前生产1千克甲种药品的成本为80元,随着生产技术的进步,现在生产1千克甲种药品的成本为60元.设甲种药品成本的年平均下降率为x,根据题意,下列方程正确的是 ( )
C.80(1-x)=60 D.80(1-2x)=60
9.[2024甘肃武威一模]如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上铺设草坪,使草坪的面积为570 m .设道路的宽为 xm,则下面所列方程正确的是 ( )
A.(32-x)(20-x)=32×20-570
B.32x+2×20x=32×20-570
C.(32-2x)(20-x)=570
[2024内蒙古通辽]如图,小程的爸爸用一段10m长的铁丝网围成一个一边靠墙(墙长5.5m)的矩形鸭舍,其面积为15m ,在鸭舍侧面中间位置留一个1m 宽的门(由其他材料制成),则BC长为 ( )
A.5m 或6m B.2.5m 或3m
C.5m D.3m
11.[2024 重庆二模]芬芳的鲜花,能驱散内心的疲惫,让人心灵得到放松,感受生活的美好.某花店抓住市场需求,计划第一次购进玫瑰和向日葵共300枝,每枝玫瑰的进价为2元,售价定为5元,每枝向日葵的进价为4元,售价定为10元.
(1)若花店在无损耗的情况下将玫瑰和向日葵全部售完,要求总获利不低于1 200元,求花店最多购进玫瑰多少枝.
(2)花店在第二次购进玫瑰和向日葵时,两种花的进价不变.由于销售火爆,花店决定购进玫瑰和向日葵共360枝,其中玫瑰的进货量在
(1)的最多进货量的基础上增加10m枝,售价比第一次提高m元,向日葵售价不变,但向日葵在运输过程中有10%已经损坏,无法进行销售,最终第二批花全部售完后销售利润为1800元,求m的值.
提升练
12.[2024辽宁丹东校级模拟]下列方程是关于x的一元二次方程的是 ( )
13.[2024黑龙江绥化]小影与小冬一起写作业,在解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是-2和-5,则原来的方程是 ( )
14.[2024 广东深圳三模]“指尖上的非遗———麻柳刺绣”,针线勾勒之间,绣出世间百态.在一幅长80 cm,宽50cm 的刺绣风景画的四周镶一圈金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5 400 cm ,设金色纸边的宽度为x cm(风景画四周的金色纸边宽度相同),则列出的方程为 ( )
A.(50+x)(80+x)=5400
B.(50-x)(80-x)=5400
C.(50+2x)(80+2x)=5400
D.(50-2x)(80-2x)=5400
15.[2024四川南充一模]关于x的方程 的两个根x ,x 满足 且x >x ,则m的值为 ( )
A.-3 B.1
C.3 D.9
16.[2024江苏扬州校级模拟]根据下表可知,方程 的一个解x的范围为 ( )
x 0.28 0.29 0.30 0.31 0.32
y=x + 3x-1 -0.0816 -0.0459 -0.01 0.0261 0.0624
A.0.28
18.[2024四川南充]已知m 是方程 的一个根,则(m+5)(m-1)的值为 .
19.[2024江苏靖江二模]若 4y·+3、则M 的最小值为 .
20.[2024 重庆B卷]重庆在低空经济领域实现了新的突破、今年第一季度低空飞行航线安全运行了200架次,预计第三季度低空飞行航线安全运行将达到401 架次.设第二、第三两个季度安全运行架次的平均增长率为x,根据题意,可列方程为 .
21.2024 重庆A卷]随着经济复苏,某公司近两年的总收入逐年递增.该公司2021年缴税40万元,2023年缴税48.4 万元.该公司这两年缴税的年平均增长率是 .
22.2024 青海 (1)解一元二次方程:
(2)若直角三角形的两边长分别是(1)中方程的根,求第三边的长.
23.[2024浙江舟山二模]小敏与小霞两位同学解方程 的过程如下:
小敏: 两边同除以(x-3),得3=x-3, 则x=6.
小霞: 移项,得:3(x-3)-(x-3) =0, 提取公因式,得(x-3)(3-x-3)=0, 则x-3=0或3-x-3=0, 解得x =3,x =0.
你认为她们的解法是否正确 若正确,请在框内打“ ”;若错误,请在框内打“×”,并写出你的解答过程.
24.[2024广东广州]关于x的方程 有两个不等的实数根.
(1)求m的取值范围;
(2)化简:
25.[2024四川内江]已知关于x的一元二次方程 (p为常数)有两个不相等的实数根x 和x .
(1)填空:
(2)求
(3)已知 求p的值.
26.[2024 辽宁一模]某校乒乓球队举行队内比赛,比赛规则是每两个队员之间都比赛一场,每场比赛都要分出胜负,每一场比赛结束后依据胜负获得相应积分,本次比赛一共进行了210场,用时两天完成,下面是第一天比赛结束后部分队员的积分表:
队员号码 比赛场次 胜场 负场 积分
1 10 8 2 18
2 10 10 0 20
3 8 7 1 15
4 8 6 2 14
5 7 0 7 7
(1)在本次比赛中,有一名队员只输掉了一场比赛,则该名队员的积分是多少
(2)如果有一名队员在本次比赛中的积分不低于34分,那么他最多负 场.
27.[2024甘肃兰州校级模拟]如图,A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点 P,Q分别从点A,C 同时出发,点 P 以 3c m/s的速度向点 B 移动,到达 B 点时停止,点Q 以2cm /s的速度向 D 点移动,当点 P 到达 B 点时点 Q 随之停止运动.设运动时间为 ts.
(1)AP = ,BP = ,CQ = ,DQ= (用含 t 的代数式表示);
(2)t为多少时,四边形 PBCQ 的面积为33cm
(3)t为多少时,点 P 和点 Q 的距离为10 cm
第7关 一元二次方程
1. A 解析:∵关于x的一元二次方程(a+ 的一个根是x=0, 且a+2≠0,解得(a=2.
2. B 解析: x(x-2)=0,x-2=0或x=0,
解得
3C 解析:
(x-3)(x-7)=0,
解得
当等腰三角形的边长是3、3、7时,3+3<7、不符合三角形的三边关系,舍去;
当等腰三角形的边长是7、7、3时,这个三角形的周长是7+7+3=17.
4. C 解析:∵方程 有两个相等的实数根,
∴4c=16,解得c=4.
5. A 解析:关于x的方程. 中,∵a=1,b=m,c=-2,
∴方程有两个不相等的实数根.
6. A 解析:∵关于x的一元二次方程. 2x+p=0两根为x ,x ,
則
7.(1)k< (2)x =-1,x =-2
解析:(1)由题意可知 17-4k>0,解得
(2)由(1)可知k=4,
∴此时方程为
∴(x+1)(x+2)=0,
8. B
9. C 解析:∵道路的宽为 xm,
∴铺设草坪的部分可合成长为(32-2x)m,宽为(20-x)m的矩形.
根据题意得(32-2x)(20-x)=570.
10. C 解析:设BC长为 xm,则AB的长为
根据题意得·
解得x=5或x=6(舍去).
故BC长为5m.
11.(1)200枝(2)m=2
解析:(1)设花店购进玫瑰x枝,则购进向日葵(300-x)枝,
根据题意得(5-2)x+(10-4)(300-x)
≥1200,
解得x≤200,
∴x的最大值为200.
答:花店最多购进玫瑰200枝.
(2)根据题意得((5+m)(200+10m)-2(200+10m)+10[360-(200+10m)]×(1-10%)-4[360-(200+10m)]=1800,
整理得
解得 (不符合题意,舍去).
答:m的值为2.
12. D 解析:A.当a=0时, 不是一元二次方程,故A 不符合题意;
不是整式方程,故B不符合题意;
是一元一次方程,故C不符合题意;
是一元二次方程,故D符合题意.
故选 D.
13. B 解析:设原来的方程为 (a≠0),
则
所以b=-7a,c=10a,
所以原来的方程为 即
14. C 解析:由题意得挂图的长为(80+2x) cm,宽为(50+2x) cm,根据题意得(50+2x)(80+2x)=5400.
15. C 解析:∵
∴(x-m+2)(x-m-2)=0,
∴x-m+2=0或x-m-2=0,
∴m+2=2(m-2)+3,
解得m=3.
故选C.
16. C 解析:∵当x=0.30时, -0.01<0,
当x=0.31|时,
∴方程 的一个解x的范围为0.30
解析:因为一元二次方程 无实数根,所以. 解得c>1.
18.-4
解析:∵m是方程. 的一个根,
19.2
解析:/ 故答案为2.
21.10%
解析:设年平均增长率是x,
则有
解得x=0.1=10%或x=-2.1(舍).
22.(1)x =1,x =3 (2)2 或
解析:
∴(x-1)(x-3)=0.
∴x-1=0或x-3=0,
(2)当3是直角三角形的斜边长时,第三边的长
当1和3是直角三角形的两直角边长时,第三边的长:
∴第三边的长为2 或
23.都错误,两框内均打“×”,解答过程见解析
解析:移项,得
提取公因式,得((x-3)(3-x+3)=0,
则x-3=0或:3-x+3=0,
解得
24.(1)m>3 (2)-2
解析:(1)∵关于x的方程 =0有两个不等的实数根,
解得m>3.
(2)∵m>3,
=-2.
25.(1)p;1
(3)p=3
解析:(1)由根与系数的关系得
∵关于x的一元二次方程 (p为常数)有两个不相等的实数根x 和
即
解得
当.p=3时,
当p=-1时 舍去.
∴p=3.
26.(1)39分 (2)6
解析:(1)设共有x个队员参加比赛,由题表得赢一场比赛得 20÷10=2(分),输掉一场比赛得7÷7=1(分),由题意得 解得x=21(负值舍去),
∴共有21个队员参加比赛,
∴每个队员一共比赛20场,(20-1)×2+1=39(分).
答:该名队员的积分是39分.
(2)设该名队员在本次比赛中负y场,由题意得(20-y)×2+y≥34,解得y≤6,
∴该名队员在本次比赛中最多负6场,故答案为6.
27.(1)3t cm;(16-3t) cm;2t cm;(16-2t) cm (2)t=5 (3) 或
解析:(1)当运动时间为 ts 时,AP=3t cm,BP=(16-3t) cm,CQ=2t cm,DQ=(16-2t) cm.
故答案为3t cm;(16-3t) cm;2t cm;(16-2t) cm.
(2)依题意得- 整理得16-t=11,
解得t=5.
答:当t为5时,四边形 PBCQ 的面积为33cm .
(3)过点 Q 作 QE⊥AB 于点 E,则 PE=|(16-3t)-2t|=|16-5t|.
依题意得|
即
解得
答:当t为 或 时,点P 和点 Q 的距离为10 cm.
同课章节目录
