第四单元《一发现潜藏的逻辑错误》 课件(共34张PPT)统编版高中语文选择性必修上册
文档属性
| 名称 | 第四单元《一发现潜藏的逻辑错误》 课件(共34张PPT)统编版高中语文选择性必修上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 统编版 | ||
| 科目 | 语文 | ||
| 更新时间 | 2025-05-20 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
逻辑的力量
下列话语中的“逻辑”是指什么
生物界遵循优胜劣汰、适者生存的逻辑。
我很难相信平行宇宙那一套逻辑。
他说的这番话完全不合逻辑。
福尔摩斯精通逻辑。
逻辑是一门独立的学问,大家都要学一点儿。
(指规律、事理。)
(指道理、理论。)
(指思维的规律。)
(指推理和论证的本领。)
(指研究思维的形式和规律,研究推理和论证的科学——逻辑学)
在本单元中要学的逻辑是指思维的规律和推理、论证的本领。
导入新课
一、发现潜藏的逻辑谬误
任务一:初识逻辑
1.逻辑是什么?
《现代汉语》释义为思维的规律和规则。
逻辑通过概念、判断来进行推理、论证,所以要学习逻辑,我们首先要了解概念以及概念之间的关系。
2.何为“概念”
①含义:心理学上认为,概念是人脑对客观事物本质的反映,这种反映是以词来标示和记载的。
概念是思维活动的结果和产物,同时又是思维活动借以进行的单元。
②概念的组成
概念的内涵∶
反映在概念中的对象的本质属性。比如说“人”这个概念的内涵是指“有语言、能思维、会制造工具的动物”。
概念的外延∶
具有概念所反映的本质属性的对象。比如“古今中外以及将来的一切人”就是“人”这个概念的外延。
是什么
有什么
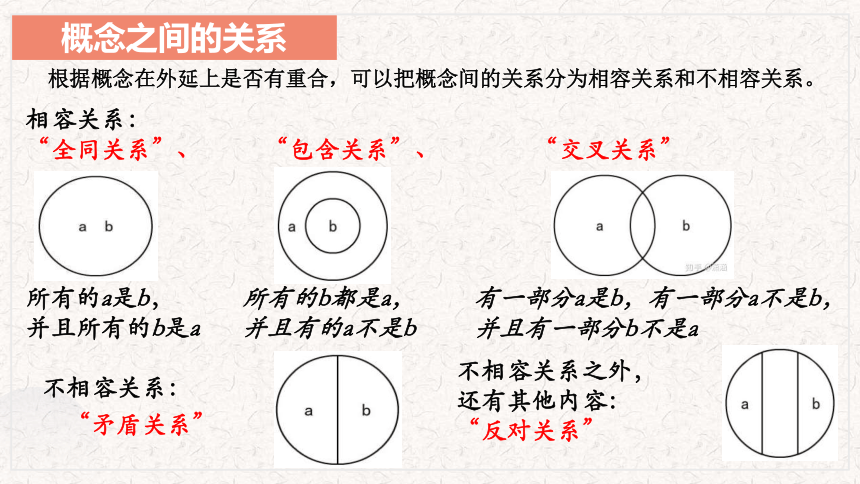
根据概念在外延上是否有重合,可以把概念间的关系分为相容关系和不相容关系。
相容关系:
“全同关系”、 “包含关系”、 “交叉关系”
不相容关系:
“矛盾关系”
概念之间的关系
所有的a是b,
并且所有的b是a
所有的b都是a,
并且有的a不是b
有一部分a是b,有一部分a不是b,
并且有一部分b不是a
不相容关系之外,
还有其他内容:
“反对关系”
“中国的首都”和“北京”
“青年”和“作家”
“大学生”和“小学生”
“战争”与“和平”
“学生”和“大学生”
“全同关系”
“反对关系”
“交叉关系”
“矛盾关系”
“包含关系”
逻辑作为思维的规律,具有这四个基本规律:
同一律
排中律
充足理由律
矛盾律(不矛盾律)
任务二:逻辑规律
PPT模板 http:///moban/
(一)同一律
“同一律”要求在同一思维过程中概念和判断具有确定性,始终保持如一。也就是概念间的关系应为“全同关系”。
违反同一律的要求的逻辑错误:“偷换概念”或者“转移论题”。
PPT模板 http:///moban/
(一)同一律
煮竹席
从前有个北方人到南方去,南方人请他吃笋。北方人没有吃过,觉得味道很鲜美,问:“这是什么 ”南方人回答:“是笋,长起来就是竹子。”北方人回到家里看见了竹席,忽然想到竹子既然是笋长起来的,竹席大概也能吃,就把竹席切碎了煮,煮来煮去不得熟。他恼了,跟妻子说; “南方人真滑头,专门戏弄人!”
尽管竹是由笋长成的,但它们是两个不同的发展阶段,有质的不同,是两个概念。北方人在这里将竹、笋两个概念搞混淆了。犯了“偷换概念”的错误。
偷换概念
张老师班会课上说:“同班同学要互相关照”,小王借作业给小明抄,被老师批评时反问道:“你不是说同班同学应该互相关照吗?”
PPT模板 http:///moban/
(一)同一律
说说下面这段话在论证上有什么毛病:
学习要讲究方法。方法对头,才能事半功倍。比如我对数学比较感兴趣,习题做得多,学习成绩就比较好;而对英语,我没有兴趣,怕读怕背,成绩就比较差。
在论证中违反同一律的要求,没有使论题保持始终如一,前面说学习要讲究方法,后面论述的是学习与兴趣的关系,这样的逻辑错误,叫转移论题,或偷换论题。
转移论题
PPT模板 http:///moban/
(二)矛盾律
又叫不矛盾律,指在同一思维过程中,两个互相矛盾或互相反对的判断不能同真,必有一假。
互相矛盾:两个命题互相矛盾,是指这两个命题不能同真,也不能同假。
互相反对:两个命题互相反对,是指这两个命题不能同真,但可以同假。
小明是个男孩子。 小明是个女孩子。
这两个命题是互相矛盾的,不能同真,也不能同假,必有一真一假;
小明在写语文作业。 小明在写数学作业。
这两个命题是互相反对的,不能同真,但可以同假。
矛盾律的要求是对两个互相矛盾或互相反对的命题,不能同时肯定,必须否定其中的一个。即A不能既是B又不是B。违反矛盾律要求的逻辑错误 :自相矛盾。
PPT模板 http:///moban/
(二)矛盾律
说说下列的表达有什么毛病:
①古时候有个人既卖矛又卖盾,有人买矛时他说:“我的矛能刺穿世上所有的盾”,有人买盾时他说:“我的盾能抵挡世上所有的矛”。
②一位小伙子在给他女朋友的信中写道:“我爱你爱得如此之深,甘愿为你赴汤蹈火。星期六若不下雨,我一定来。”
自相矛盾,违反矛盾律。
PPT模板 http:///moban/
(三)排中律
指在同一思维过程中,两个互相矛盾的判断不能同假,必有一真。排中律要求不能同时否定相互否定的思想。任何事物在明确的条件下,都要有明确的“是”或“非”的判断,不存在中间状态。
例如,在数学上,一个数字,要么大于零,要么不大于零,没有中间状态。违反排中律要求的逻辑错误:“两不可” 、“模棱两可”
例如,“你的项目,不能说成功了,也不能说没有成功。”如果这里的两个“成功”内涵和外延完全相同,则违反排中律,犯了“模棱两可”的错误,如果内涵和外延不同,则违反了同一律“偷换概念”的错误。
PPT模板 http:///moban/
(三)排中律
例2.在讨论是否应该禁烟时,甲说:“我不赞成禁烟,烟草可是国家的一项重要产业。可是,毕竟吸烟危害人的健康,所以,我也不赞成不禁烟的意见。”
“模棱两可”
例1.有一块空地可以种庄稼,甲、乙两人讨论这块地该种什么庄稼好。甲一会儿说应该种玉米,一会儿又说不应该种玉米。针对甲的说法,乙说: “你的两种意见,我都不同意。”
在这里,甲的说法就违反了矛盾律的要求,犯了“自相矛盾”的错误,因为他同时肯定了这块空地“应该种玉米”和“不应该种玉米”这两个相互矛盾的判断。而针对甲的说法,乙的说法就违反了排中律的要求,因为排中律认为两个互相矛盾的判断不能同假。犯了“两不可”的错误。
PPT模板 http:///moban/
(三)排中律
雷蒙德·斯穆里安(Raymond Smullyan)是普林斯顿大学的博士生,一天他去纽约玩,遇到了一位非常迷人的女音乐家,斯穆里安对女音乐家说:“我们来做个游戏吧,我说一句话,如果这句话是真的,可以给我你的签名吗?”女音乐家饶有兴致地说:“当然,但如果你说的不是真的,我就不会给你”。“好的……你既不会给我签名也不会给我一个吻”。就这样,斯穆里安巧妙地运用逻辑学赢得了一个香吻。为什么呢?
排中律不能有中项,斯穆里安利用排中律增加了中项,“你既不会给我签名也不会给我一个吻”如果是真,则要签名,自相矛盾,只能是假,则“也不会给我一个吻”必是假。
PPT模板 http:///moban/
排中律与矛盾律的区别
1.矛盾律:两个互相矛盾或者互相反对的命题,不能同时为真,必有一假。
2.排中律:两个互相矛盾的命题,不能同时为假,必有一真。
对比两个定律的叙述可以发现,最主要的不同是:矛盾律中包含了互相矛盾和互相反对的命题的判断,而排中律则只包含了对互相矛盾的命题的判断。
互相矛盾,是指两个命题不能同真,也不能同假。互相反对,是这两个命题不能同真,但可以同假。
例如“小张是湖南人”和“小张不是湖南人” 这两个命题是互相矛盾的,不能同真,也不能同假,必有一真一假;而“小张是湖南人”和“小张是江西人”这两个命题是互相反对的,不能同真,但可以同假。
对于一个命题该到底该应用哪一个定律,首先判断涉及到的两个命题是互相矛盾的还是互相反对的,如果是互相反对的,只能使用矛盾律;如果是互相矛盾的,而且是同时肯定两个命题,则违反了矛盾律,因为矛盾律规定不能同时为真,必有一假;如果是同时否定两个命题,则违反了排中律,因为排中律规定不能同时为假,必有一真。
PPT模板 http:///moban/
(四)充足理由律
在同一思维和论证过程中,一个思想被确定为真,要有充足的理由。要点:①对所要论证的观点必须给出理由。②给出的理由必须真实。③从给出的理由必须能够推出所要论证的论点。
常见的逻辑错误:“没有理由”“理由虚假”“推不出来”。
如:①送来的时候还好好的,怎么到你们医院之后就不行了呢?②小李结婚后就离开了公司,一定是他新婚夫人让他辞去这份工作的。③没撞,你为什么要扶?
①②都是因为时间上的接近就强加了前者和后者的因果关系,违背充足理由律。③“没撞”推不出“要扶”,强加因果,违背充足理由律。
逻辑规律 公式 要求 (同一时间同一方面对 同一对象) 逻辑错误
同一律 A是A 如果是真就是真 如果是假就是假 偷换概念;
偷换论题;
矛盾律 A不是非A 不能同时肯定 不能同真,必有一假 (矛盾关系、反对关系) 自相矛盾(两可);
排中律 A或者非A 不能同时否定 不能同假,必有一真 (矛盾关系) 两不可;模棱两可
充分理由律 A真; 因为B真, 并且B能推出A 一要有理由 二要理由真 三是必然推导 没有理由;
虚假理由;
推不出来;
逻辑谬误特指具有一定迷惑性的逻辑错误。一般指思维过程中违反逻辑规律的要求和逻辑规则而产生的错误。如概念的含义前后不一致,立场自相矛盾、态度模棱两可,理由站不住脚或推不出结论等。
任务三:合作探究,发现逻辑谬误
任务三:合作探究,发现逻辑谬误
①鲁迅的作品不是一天能读完的,《孔乙己》是鲁迅的作品,所以,《孔乙己》不是一天能读完的。
“鲁迅的作品”和“《孔乙己》”是“包含关系”,不是“全同关系”,违反“同一律”。犯了“偷换概念”的错误。
(《逻辑的力量P69》和课本)
②庄子曰:“请循其本。子曰‘汝安知鱼乐’云者,既已知吾知之而问我,我知之濠上也。“
分析:“安”,在问句中通常有两种用法,一种表示“怎么”,一种表示“哪里”。惠子问的是“你怎么知道鱼是快乐的”,是问原因,庄子回答“是在濠上这个地方知道的”,是答地点,答非所问,违反了“同一律”,犯了“偷换概念”的错误。
③“服务员同志,请当心,你的手指浸到我的汤里去了。“
“没有关系,汤不烫,我不痛。”
分析:顾客说的意思是“你弄脏了我的汤”,而服务员的回答是以为顾客关心他痛不痛,答非所问,违反了“同一律”,犯了“转移话题”的错误。
④“我是答应您昨天来修门铃没错。可我来了三次,每次按门铃,都没有人来开门,我只好走了。”
明确:“修门铃”说明“门铃坏了”与“按门铃有人开门(没坏)”,自相矛盾,二者必有一假,违反矛盾律(或“不矛盾律”)。
⑤在法国某地,一个耍戏法的人招揽观众:“快来快来,这里有拿破仑的头骨。”围观的一个人说:“奇怪,听说拿破仑的脑袋是很大的,这个头骨怎么和普通人的没有区别啊?”耍戏法的人解释道:“没错,这是拿破仑小时候的头骨。”
“头骨小”和“小时候的头骨”不是同一个概念,耍戏法的人在偷换概念,违反了“同一律”。
再者,“拿破仑小时候的头骨”意思是“拿破仑夭折了”,与事实“拿破仑并未夭折”互相矛盾了,又违反了“矛盾律”。
⑥有人说,《红楼梦》值得读,有人说不值得,两种意见我都不赞成:读,太花时间;不读,又有点儿可惜。
分析:“两种意见我都不赞成”的说法错误,《红楼梦》“值得读”和“不值得读”是互相矛盾的,不能都否定;都否定违反了排中律,要么赞成读,要么赞成不读。
⑦不薄之谓厚,不白之谓黑。
厚薄之间还存在着不厚不薄,黑与白之间还存在其他颜色,是反对关系,属于“排中律”使用不当。
⑧《祝福》中,鲁四老爷知道祥林嫂的死讯后说:“不早不迟,偏偏在这时候,——这就可见是一个谬种!”
用一个人的死亡时间,推测出“是一个谬种”的结论,违反“充足理由律”。
⑨你是否已经停止了对我的诽谤?请回答“是”或者“不是”!
分析:“你是否已经停止了对我的诽谤”,隐藏着一个前提,那就是对方一直在诽谤说话人。对方无论回答肯定还是否定,都意味着承认这个前提。而这个前提可能是虚假的。这种错误叫做“不当预设”,违反了排中律。
逻辑谬误和故意违反逻辑的语言艺术是有区别的。前者为无意为之,后者为有意为之。后者虽然违反了逻辑的规律,却让人体会到高妙的语言艺术,让人会心一笑。
请看:
欣赏逻辑谬误带来的艺术效果
①齐高帝曾与王僧虔赌书毕,帝曰:“谁为第一?”僧虔对曰:“臣书人臣中第一,陛下书帝中第一。”(P73)
赏析:齐高帝的意思是所有人放在一起比谁是第一?王僧虔故意曲解,把人分为了两类,让齐高帝和自己都得了第一,既保全了高帝的颜面,又保留了自己的尊严,而且还没有违背自己眼中的事实,不因为对方高高在上就阿谀奉承,也没有为了无关体统的事就冒上犯颜,体现了较高的语言艺术。
欣赏逻辑谬误带来的艺术效果
②有一次外事活动中,有位外国记者用嘲讽的口吻对周总理说:“你们中国人走路都是弯腰的,而我们却是挺直着胸膛走。周先生,您说是吗?”此话一出,语惊四座。周恩来不慌不忙,脸带微笑地说:“这并不奇怪,因为我们中国人喜欢走上坡路,而你们美国人喜欢走下坡路。”
赏析:弯腰走路、挺着胸膛走的“路”,其实是指现实生活中的路,“上坡路”和“下坡路”的“路”是国家的发展之路,这两个“路”全然不是一个概念。周恩来的回答虽违背了同一律,但却堪称语言艺术,“上坡下坡”有利反击了对方的挑衅。
分析逻辑谬误带来的艺术效果
臧克家《有的人》:有的人活着,他已经死了;有的人死了,他还活着。
在“死”与“活”的矛盾中,反映出诗人内心对精神不朽、虽死犹生的鲁迅先生的敬仰,对欺压人民、虽生犹死者的鄙夷的复杂情感交织。
表面上背离了形式逻辑,实际上更加深刻地揭示了心灵逻辑。
《威尼斯商人》经典情节(P65)
女主人公鲍西亚对求婚者说:“这里有三只盒子:一只是金盒子,一只是银盒子,一只是铅盒子,每只盒子上各写有一句话。三句话中,只有一句是真话。谁能猜中我的肖像放在哪一只盒子里,谁就能做我的丈夫。”
金盒上写的是“肖像在这里”,
银盒上写的是“肖像不在这里”,
铅盒上写的是“肖像不在金盒里”。
经过逻辑推断,你认为肖像应该在哪个盒子里?
逻辑分析:因为金盒子上的话和铅盒子上的话是矛盾的,所以两句中一真一假。其次,三句话中至多只有一句是真话,所以银盒上的是假话。
画像在银盒里。
新知讲解
【2016.山东卷】该型飞机在运营成本上是其他同级别机型的1.3至2倍,优势明显;在商载、航程、航速等方面也极具竞争力。
“在运营成本上是其他同级别机型的1.3至2倍”是劣势,而不是优势。
【2015.湖北卷】近年来,生态保护意识渐入人心,所以当社会经济发展与林地保护管理发生冲突时,一些地方在权衡之后往往会选择前者。
既然“生态保护意识渐入人心”,那么“一些地方在权衡之后往往会选择前者”明显与前文矛盾,应改为“选择后者”。
自相矛盾
课 堂 小 结
概 念
相容关系
不相容关系
逻辑基本规律
发现潜藏的逻辑谬误
辨别谬误
矛盾关系
交叉关系
包含关系
全同关系
充足理由律
排中律
矛盾律(不矛盾律)
同一律
反对关系
逻辑的力量
下列话语中的“逻辑”是指什么
生物界遵循优胜劣汰、适者生存的逻辑。
我很难相信平行宇宙那一套逻辑。
他说的这番话完全不合逻辑。
福尔摩斯精通逻辑。
逻辑是一门独立的学问,大家都要学一点儿。
(指规律、事理。)
(指道理、理论。)
(指思维的规律。)
(指推理和论证的本领。)
(指研究思维的形式和规律,研究推理和论证的科学——逻辑学)
在本单元中要学的逻辑是指思维的规律和推理、论证的本领。
导入新课
一、发现潜藏的逻辑谬误
任务一:初识逻辑
1.逻辑是什么?
《现代汉语》释义为思维的规律和规则。
逻辑通过概念、判断来进行推理、论证,所以要学习逻辑,我们首先要了解概念以及概念之间的关系。
2.何为“概念”
①含义:心理学上认为,概念是人脑对客观事物本质的反映,这种反映是以词来标示和记载的。
概念是思维活动的结果和产物,同时又是思维活动借以进行的单元。
②概念的组成
概念的内涵∶
反映在概念中的对象的本质属性。比如说“人”这个概念的内涵是指“有语言、能思维、会制造工具的动物”。
概念的外延∶
具有概念所反映的本质属性的对象。比如“古今中外以及将来的一切人”就是“人”这个概念的外延。
是什么
有什么
根据概念在外延上是否有重合,可以把概念间的关系分为相容关系和不相容关系。
相容关系:
“全同关系”、 “包含关系”、 “交叉关系”
不相容关系:
“矛盾关系”
概念之间的关系
所有的a是b,
并且所有的b是a
所有的b都是a,
并且有的a不是b
有一部分a是b,有一部分a不是b,
并且有一部分b不是a
不相容关系之外,
还有其他内容:
“反对关系”
“中国的首都”和“北京”
“青年”和“作家”
“大学生”和“小学生”
“战争”与“和平”
“学生”和“大学生”
“全同关系”
“反对关系”
“交叉关系”
“矛盾关系”
“包含关系”
逻辑作为思维的规律,具有这四个基本规律:
同一律
排中律
充足理由律
矛盾律(不矛盾律)
任务二:逻辑规律
PPT模板 http:///moban/
(一)同一律
“同一律”要求在同一思维过程中概念和判断具有确定性,始终保持如一。也就是概念间的关系应为“全同关系”。
违反同一律的要求的逻辑错误:“偷换概念”或者“转移论题”。
PPT模板 http:///moban/
(一)同一律
煮竹席
从前有个北方人到南方去,南方人请他吃笋。北方人没有吃过,觉得味道很鲜美,问:“这是什么 ”南方人回答:“是笋,长起来就是竹子。”北方人回到家里看见了竹席,忽然想到竹子既然是笋长起来的,竹席大概也能吃,就把竹席切碎了煮,煮来煮去不得熟。他恼了,跟妻子说; “南方人真滑头,专门戏弄人!”
尽管竹是由笋长成的,但它们是两个不同的发展阶段,有质的不同,是两个概念。北方人在这里将竹、笋两个概念搞混淆了。犯了“偷换概念”的错误。
偷换概念
张老师班会课上说:“同班同学要互相关照”,小王借作业给小明抄,被老师批评时反问道:“你不是说同班同学应该互相关照吗?”
PPT模板 http:///moban/
(一)同一律
说说下面这段话在论证上有什么毛病:
学习要讲究方法。方法对头,才能事半功倍。比如我对数学比较感兴趣,习题做得多,学习成绩就比较好;而对英语,我没有兴趣,怕读怕背,成绩就比较差。
在论证中违反同一律的要求,没有使论题保持始终如一,前面说学习要讲究方法,后面论述的是学习与兴趣的关系,这样的逻辑错误,叫转移论题,或偷换论题。
转移论题
PPT模板 http:///moban/
(二)矛盾律
又叫不矛盾律,指在同一思维过程中,两个互相矛盾或互相反对的判断不能同真,必有一假。
互相矛盾:两个命题互相矛盾,是指这两个命题不能同真,也不能同假。
互相反对:两个命题互相反对,是指这两个命题不能同真,但可以同假。
小明是个男孩子。 小明是个女孩子。
这两个命题是互相矛盾的,不能同真,也不能同假,必有一真一假;
小明在写语文作业。 小明在写数学作业。
这两个命题是互相反对的,不能同真,但可以同假。
矛盾律的要求是对两个互相矛盾或互相反对的命题,不能同时肯定,必须否定其中的一个。即A不能既是B又不是B。违反矛盾律要求的逻辑错误 :自相矛盾。
PPT模板 http:///moban/
(二)矛盾律
说说下列的表达有什么毛病:
①古时候有个人既卖矛又卖盾,有人买矛时他说:“我的矛能刺穿世上所有的盾”,有人买盾时他说:“我的盾能抵挡世上所有的矛”。
②一位小伙子在给他女朋友的信中写道:“我爱你爱得如此之深,甘愿为你赴汤蹈火。星期六若不下雨,我一定来。”
自相矛盾,违反矛盾律。
PPT模板 http:///moban/
(三)排中律
指在同一思维过程中,两个互相矛盾的判断不能同假,必有一真。排中律要求不能同时否定相互否定的思想。任何事物在明确的条件下,都要有明确的“是”或“非”的判断,不存在中间状态。
例如,在数学上,一个数字,要么大于零,要么不大于零,没有中间状态。违反排中律要求的逻辑错误:“两不可” 、“模棱两可”
例如,“你的项目,不能说成功了,也不能说没有成功。”如果这里的两个“成功”内涵和外延完全相同,则违反排中律,犯了“模棱两可”的错误,如果内涵和外延不同,则违反了同一律“偷换概念”的错误。
PPT模板 http:///moban/
(三)排中律
例2.在讨论是否应该禁烟时,甲说:“我不赞成禁烟,烟草可是国家的一项重要产业。可是,毕竟吸烟危害人的健康,所以,我也不赞成不禁烟的意见。”
“模棱两可”
例1.有一块空地可以种庄稼,甲、乙两人讨论这块地该种什么庄稼好。甲一会儿说应该种玉米,一会儿又说不应该种玉米。针对甲的说法,乙说: “你的两种意见,我都不同意。”
在这里,甲的说法就违反了矛盾律的要求,犯了“自相矛盾”的错误,因为他同时肯定了这块空地“应该种玉米”和“不应该种玉米”这两个相互矛盾的判断。而针对甲的说法,乙的说法就违反了排中律的要求,因为排中律认为两个互相矛盾的判断不能同假。犯了“两不可”的错误。
PPT模板 http:///moban/
(三)排中律
雷蒙德·斯穆里安(Raymond Smullyan)是普林斯顿大学的博士生,一天他去纽约玩,遇到了一位非常迷人的女音乐家,斯穆里安对女音乐家说:“我们来做个游戏吧,我说一句话,如果这句话是真的,可以给我你的签名吗?”女音乐家饶有兴致地说:“当然,但如果你说的不是真的,我就不会给你”。“好的……你既不会给我签名也不会给我一个吻”。就这样,斯穆里安巧妙地运用逻辑学赢得了一个香吻。为什么呢?
排中律不能有中项,斯穆里安利用排中律增加了中项,“你既不会给我签名也不会给我一个吻”如果是真,则要签名,自相矛盾,只能是假,则“也不会给我一个吻”必是假。
PPT模板 http:///moban/
排中律与矛盾律的区别
1.矛盾律:两个互相矛盾或者互相反对的命题,不能同时为真,必有一假。
2.排中律:两个互相矛盾的命题,不能同时为假,必有一真。
对比两个定律的叙述可以发现,最主要的不同是:矛盾律中包含了互相矛盾和互相反对的命题的判断,而排中律则只包含了对互相矛盾的命题的判断。
互相矛盾,是指两个命题不能同真,也不能同假。互相反对,是这两个命题不能同真,但可以同假。
例如“小张是湖南人”和“小张不是湖南人” 这两个命题是互相矛盾的,不能同真,也不能同假,必有一真一假;而“小张是湖南人”和“小张是江西人”这两个命题是互相反对的,不能同真,但可以同假。
对于一个命题该到底该应用哪一个定律,首先判断涉及到的两个命题是互相矛盾的还是互相反对的,如果是互相反对的,只能使用矛盾律;如果是互相矛盾的,而且是同时肯定两个命题,则违反了矛盾律,因为矛盾律规定不能同时为真,必有一假;如果是同时否定两个命题,则违反了排中律,因为排中律规定不能同时为假,必有一真。
PPT模板 http:///moban/
(四)充足理由律
在同一思维和论证过程中,一个思想被确定为真,要有充足的理由。要点:①对所要论证的观点必须给出理由。②给出的理由必须真实。③从给出的理由必须能够推出所要论证的论点。
常见的逻辑错误:“没有理由”“理由虚假”“推不出来”。
如:①送来的时候还好好的,怎么到你们医院之后就不行了呢?②小李结婚后就离开了公司,一定是他新婚夫人让他辞去这份工作的。③没撞,你为什么要扶?
①②都是因为时间上的接近就强加了前者和后者的因果关系,违背充足理由律。③“没撞”推不出“要扶”,强加因果,违背充足理由律。
逻辑规律 公式 要求 (同一时间同一方面对 同一对象) 逻辑错误
同一律 A是A 如果是真就是真 如果是假就是假 偷换概念;
偷换论题;
矛盾律 A不是非A 不能同时肯定 不能同真,必有一假 (矛盾关系、反对关系) 自相矛盾(两可);
排中律 A或者非A 不能同时否定 不能同假,必有一真 (矛盾关系) 两不可;模棱两可
充分理由律 A真; 因为B真, 并且B能推出A 一要有理由 二要理由真 三是必然推导 没有理由;
虚假理由;
推不出来;
逻辑谬误特指具有一定迷惑性的逻辑错误。一般指思维过程中违反逻辑规律的要求和逻辑规则而产生的错误。如概念的含义前后不一致,立场自相矛盾、态度模棱两可,理由站不住脚或推不出结论等。
任务三:合作探究,发现逻辑谬误
任务三:合作探究,发现逻辑谬误
①鲁迅的作品不是一天能读完的,《孔乙己》是鲁迅的作品,所以,《孔乙己》不是一天能读完的。
“鲁迅的作品”和“《孔乙己》”是“包含关系”,不是“全同关系”,违反“同一律”。犯了“偷换概念”的错误。
(《逻辑的力量P69》和课本)
②庄子曰:“请循其本。子曰‘汝安知鱼乐’云者,既已知吾知之而问我,我知之濠上也。“
分析:“安”,在问句中通常有两种用法,一种表示“怎么”,一种表示“哪里”。惠子问的是“你怎么知道鱼是快乐的”,是问原因,庄子回答“是在濠上这个地方知道的”,是答地点,答非所问,违反了“同一律”,犯了“偷换概念”的错误。
③“服务员同志,请当心,你的手指浸到我的汤里去了。“
“没有关系,汤不烫,我不痛。”
分析:顾客说的意思是“你弄脏了我的汤”,而服务员的回答是以为顾客关心他痛不痛,答非所问,违反了“同一律”,犯了“转移话题”的错误。
④“我是答应您昨天来修门铃没错。可我来了三次,每次按门铃,都没有人来开门,我只好走了。”
明确:“修门铃”说明“门铃坏了”与“按门铃有人开门(没坏)”,自相矛盾,二者必有一假,违反矛盾律(或“不矛盾律”)。
⑤在法国某地,一个耍戏法的人招揽观众:“快来快来,这里有拿破仑的头骨。”围观的一个人说:“奇怪,听说拿破仑的脑袋是很大的,这个头骨怎么和普通人的没有区别啊?”耍戏法的人解释道:“没错,这是拿破仑小时候的头骨。”
“头骨小”和“小时候的头骨”不是同一个概念,耍戏法的人在偷换概念,违反了“同一律”。
再者,“拿破仑小时候的头骨”意思是“拿破仑夭折了”,与事实“拿破仑并未夭折”互相矛盾了,又违反了“矛盾律”。
⑥有人说,《红楼梦》值得读,有人说不值得,两种意见我都不赞成:读,太花时间;不读,又有点儿可惜。
分析:“两种意见我都不赞成”的说法错误,《红楼梦》“值得读”和“不值得读”是互相矛盾的,不能都否定;都否定违反了排中律,要么赞成读,要么赞成不读。
⑦不薄之谓厚,不白之谓黑。
厚薄之间还存在着不厚不薄,黑与白之间还存在其他颜色,是反对关系,属于“排中律”使用不当。
⑧《祝福》中,鲁四老爷知道祥林嫂的死讯后说:“不早不迟,偏偏在这时候,——这就可见是一个谬种!”
用一个人的死亡时间,推测出“是一个谬种”的结论,违反“充足理由律”。
⑨你是否已经停止了对我的诽谤?请回答“是”或者“不是”!
分析:“你是否已经停止了对我的诽谤”,隐藏着一个前提,那就是对方一直在诽谤说话人。对方无论回答肯定还是否定,都意味着承认这个前提。而这个前提可能是虚假的。这种错误叫做“不当预设”,违反了排中律。
逻辑谬误和故意违反逻辑的语言艺术是有区别的。前者为无意为之,后者为有意为之。后者虽然违反了逻辑的规律,却让人体会到高妙的语言艺术,让人会心一笑。
请看:
欣赏逻辑谬误带来的艺术效果
①齐高帝曾与王僧虔赌书毕,帝曰:“谁为第一?”僧虔对曰:“臣书人臣中第一,陛下书帝中第一。”(P73)
赏析:齐高帝的意思是所有人放在一起比谁是第一?王僧虔故意曲解,把人分为了两类,让齐高帝和自己都得了第一,既保全了高帝的颜面,又保留了自己的尊严,而且还没有违背自己眼中的事实,不因为对方高高在上就阿谀奉承,也没有为了无关体统的事就冒上犯颜,体现了较高的语言艺术。
欣赏逻辑谬误带来的艺术效果
②有一次外事活动中,有位外国记者用嘲讽的口吻对周总理说:“你们中国人走路都是弯腰的,而我们却是挺直着胸膛走。周先生,您说是吗?”此话一出,语惊四座。周恩来不慌不忙,脸带微笑地说:“这并不奇怪,因为我们中国人喜欢走上坡路,而你们美国人喜欢走下坡路。”
赏析:弯腰走路、挺着胸膛走的“路”,其实是指现实生活中的路,“上坡路”和“下坡路”的“路”是国家的发展之路,这两个“路”全然不是一个概念。周恩来的回答虽违背了同一律,但却堪称语言艺术,“上坡下坡”有利反击了对方的挑衅。
分析逻辑谬误带来的艺术效果
臧克家《有的人》:有的人活着,他已经死了;有的人死了,他还活着。
在“死”与“活”的矛盾中,反映出诗人内心对精神不朽、虽死犹生的鲁迅先生的敬仰,对欺压人民、虽生犹死者的鄙夷的复杂情感交织。
表面上背离了形式逻辑,实际上更加深刻地揭示了心灵逻辑。
《威尼斯商人》经典情节(P65)
女主人公鲍西亚对求婚者说:“这里有三只盒子:一只是金盒子,一只是银盒子,一只是铅盒子,每只盒子上各写有一句话。三句话中,只有一句是真话。谁能猜中我的肖像放在哪一只盒子里,谁就能做我的丈夫。”
金盒上写的是“肖像在这里”,
银盒上写的是“肖像不在这里”,
铅盒上写的是“肖像不在金盒里”。
经过逻辑推断,你认为肖像应该在哪个盒子里?
逻辑分析:因为金盒子上的话和铅盒子上的话是矛盾的,所以两句中一真一假。其次,三句话中至多只有一句是真话,所以银盒上的是假话。
画像在银盒里。
新知讲解
【2016.山东卷】该型飞机在运营成本上是其他同级别机型的1.3至2倍,优势明显;在商载、航程、航速等方面也极具竞争力。
“在运营成本上是其他同级别机型的1.3至2倍”是劣势,而不是优势。
【2015.湖北卷】近年来,生态保护意识渐入人心,所以当社会经济发展与林地保护管理发生冲突时,一些地方在权衡之后往往会选择前者。
既然“生态保护意识渐入人心”,那么“一些地方在权衡之后往往会选择前者”明显与前文矛盾,应改为“选择后者”。
自相矛盾
课 堂 小 结
概 念
相容关系
不相容关系
逻辑基本规律
发现潜藏的逻辑谬误
辨别谬误
矛盾关系
交叉关系
包含关系
全同关系
充足理由律
排中律
矛盾律(不矛盾律)
同一律
反对关系
