第8章综合训练--2025人教A版数学必修第二册同步练习题(含解析)
文档属性
| 名称 | 第8章综合训练--2025人教A版数学必修第二册同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 550.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 11:04:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教A版数学必修第二册
综合训练
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.[2024安徽合肥高一期末]如图,△A'B'C'是用斜二测画法画出的水平放置的△ABC的直观图,其中B'C'=C'A'=1,A'B'∥x'轴,A'C'∥y'轴,则BC=( )
A. B.2 C. D.4
2.某圆锥高为,母线与底面所成的角为,则该圆锥的表面积为( )
A.3π B.4π
C.5π D.6π
3.[2024山西太原高一期末]已知m,n是两条不同的直线,α,β是两个不重合的平面,则下列命题正确的是( )
A.若m∥n,m∥α,n∥β,则α∥β
B.若α∥β,m∥α,n β,则m∥n
C.若m⊥n,m⊥α,n⊥β,则α⊥β
D.若α⊥β,m∥α,n∥β,则m⊥n
4.在等腰直角三角形ABC中,AB=BC=1,M为AC的中点,沿BM把它折成二面角,折后点A与点C的距离为1,则二面角C-BM-A的大小为( )
A.30° B.60°
C.90° D.120°
5.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,则四边形ABCD绕AD所在直线旋转一周所成几何体的表面积为( )
A.(60+4)π B.(60+8)π
C.(56+8)π D.(56+4)π
6.在空间四边形ABCD中,AD=2,BC=2,E,F分别是AB,CD的中点,EF=,则异面直线AD与BC所成角的大小为( )
A.150° B.60°
C.120° D.30°
7.如图,正方体ABCD-A1B1C1D1的棱长为1,动点E在线段A1C1上,F,M分别是AD,CD的中点,则下列结论错误的是( )
A.FM∥A1C1
B.当E为A1C1中点时,BE⊥FM
C.三棱锥B-CEF的体积为定值
D.存在点E,使得平面BEF∥平面CC1D1D
8.已知三棱锥P-ABC的高为1,底面三角形ABC为等边三角形,PA=PB=PC,且P,A,B,C都在体积为的球O的表面上,则该三棱锥的底面三角形ABC的边长为( )
A. B.
C.3 D.2
二、选择题:在每小题给出的选项中,有多项符合题目要求.
9.如图,圆柱的轴截面是四边形ABCD,E是底面圆周上异于A,B的一点,则下列结论中正确的是( )
A.AE⊥CE
B.BE⊥DE
C.DE⊥平面CEB
D.平面ADE⊥平面BCE
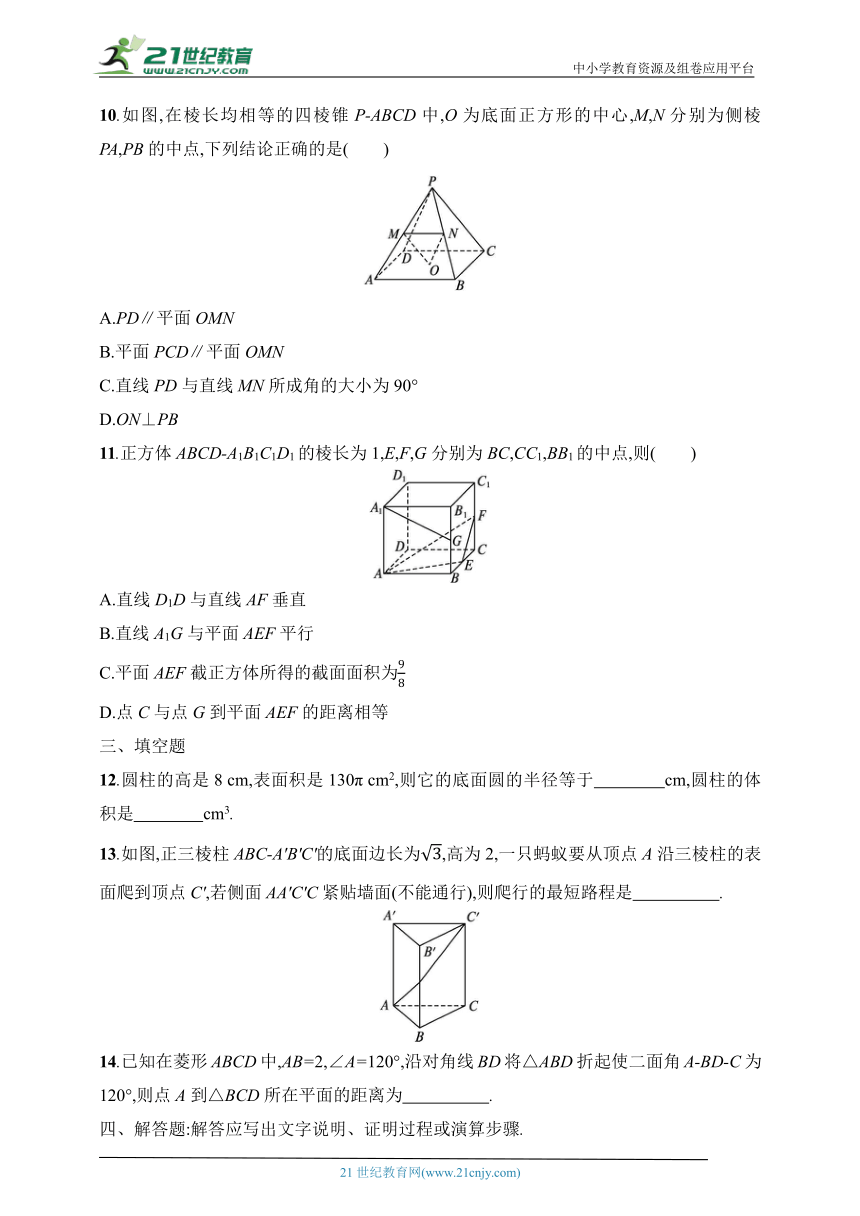
10.如图,在棱长均相等的四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,下列结论正确的是( )
A.PD∥平面OMN
B.平面PCD∥平面OMN
C.直线PD与直线MN所成角的大小为90°
D.ON⊥PB
11.正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点,则( )
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C与点G到平面AEF的距离相等
三、填空题
12.圆柱的高是8 cm,表面积是130π cm2,则它的底面圆的半径等于 cm,圆柱的体积是 cm3.
13.如图,正三棱柱ABC-A'B'C'的底面边长为,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C',若侧面AA'C'C紧贴墙面(不能通行),则爬行的最短路程是 .
14.已知在菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起使二面角A-BD-C为120°,则点A到△BCD所在平面的距离为 .
四、解答题:解答应写出文字说明、证明过程或演算步骤.
15.某种“笼具”由上、下两层组成,上层和下层分别是一个圆锥和一个圆柱,其中圆柱与圆锥的底面半径相等,如图所示,圆锥无底面,圆柱无上底面有下底面,内部镂空,已知圆锥的母线长为20 cm,圆柱高为30 cm,底面的周长为24π cm.
(1)求这种“笼具”的体积(π取3.14,结果精确到0.1 cm3);
(2)现要使用一种纱网材料制作这样“笼具”的保护罩(包括底面)50个,该保护罩紧贴包裹“笼具”,纱网材料(按实测面积计算)的造价为每平方米8元,共需多少元 (结果精确到0.1元)
16.[2024内蒙古包头高一月考]如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AD=2,E为PB的中点,F为AC与BD的交点.
(1)证明:EF∥平面PCD;
(2)求三棱锥E-ABF的体积.
17.如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=1,M,N,Q分别为AC,B1C1,CC1的中点.求证:
(1)MN∥平面ABB1A1;
(2)A1B⊥平面MNQ.
18.[2024河北沧州高一期末]如图,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面四边形ABCD为矩形,且平面PAD⊥平面ABCD,M,N分别为AB,AD的中点,二面角D-PN-C的正切值为2.
(1)求四棱锥P-ABCD的体积;
(2)证明:DM⊥PC;
(3)求直线PM与平面PNC所成角的正弦值.
19.[2024吉林长春高一检测]如图1,在等边三角形ABC中,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD,如图2.
图1
图2
(1)求证:AB∥平面DEF.
(2)在线段BC上是否存在一点P,使AP⊥DE 若存在,求的值;若不存在,请说明理由.
第八章综合训练
1.C 在△A'B'C'中,B'C'=C'A'=1,∠B'A'C'=45°,
由余弦定理可得B'C'2=A'C'2+A'B'2-2A'C'·A'B'·cos 45°,
即A'B'2-A'B'=0,而A'B'>0,解得A'B'=.
由斜二测画法可知,在△ABC中,AB⊥AC,AB=A'B'=,AC=2C'A'=2,
故BC=.
故选C.
2.A 由圆锥高为,母线与底面所成的角为,得圆锥底面圆半径r==1,母线l==2,所以圆锥的表面积S=πr2+πrl=3π.
故选A.
3.C 对于A,若m∥n,m∥α,n∥β,当m,n都平行于α与β的交线时,满足条件,此时α与β相交,故A错误;
对于B,若α∥β,m∥α,n β,则m,n可能异面,故B错误;
对于C,若m⊥n,m⊥α,n⊥β,则α⊥β,故C正确;
对于D,若α⊥β,m∥α,n∥β,则m,n可能平行或异面,故D错误.
故选C.
4.C
如图,由A'B=BC=1,∠A'BC=90°知A'C=.
∵M为A'C的中点,∴MC=AM=,且CM⊥BM,AM⊥BM,
∴∠CMA为二面角C-BM-A的平面角.
∵AC=1,MC=MA=,∴∠CMA=90°,故选C.
5.
A 四边形ABCD绕AD所在直线旋转一周所成的几何体,如图.
S表面=S圆台下底面+S圆台侧面+S圆锥侧面=+π(r1+r2)l2+πr1l1=π×52+π×(2+5)×5+π×2×2=(60+4)π.故选A.
6.D
如图所示.设BD的中点为O,连接EO,FO,所以EO∥AD,FO∥BC,则∠EOF是AD,BC所成的角或其补角,
又EO=AD=1,FO=BC=,EF=,
根据余弦定理,得cos∠EOF==-,
所以∠EOF=150°,异面直线AD与BC所成的角为30°.
7.D 连接AC,在正方体ABCD-A1B1C1D1中,因为AA1=CC1且AA1∥CC1,
所以四边形AA1C1C为平行四边形,则AC∥A1C1.
因为F,M分别是AD,CD的中点,所以FM∥AC∥A1C1,故A正确;
连接BA1,在正方体ABCD-A1B1C1D1中,BA1=BC1,当E为A1C1的中点时,BE⊥A1C1,所以BE⊥FM,故B正确;
因为三棱锥B-CEF的体积即为三棱锥E-BCF的体积,在三棱锥E-BCF中,底面三角形BCF的面积为定值,棱锥的高等于AA1,为定值,三棱锥E-BCF的体积为定值,则三棱锥B-CEF的体积为定值,故C正确;
直线BF与平面CC1D1D有交点,所以不存在点E,使得平面BEF∥平面CC1D1D,故D错误.故选D.
8.C 设球O的半径为R,由球的体积为可得,R3=,解得R=2.
因为三棱锥P-ABC的高h为1,所以球心O在三棱锥外.
如图,设点O1为△ABC的外心,则OO1⊥平面ABC.
在Rt△AO1O中,由A=OA2-O,且OO1=R-h=1,得AO1=.
因为△ABC为等边三角形,所以AO1=AB·sin 60°=AB,所以AB=AO1=3.故选C.
9.ABD 由AB是底面圆的直径,得∠AEB=90°,即AE⊥EB.
∵圆柱的轴截面是四边形ABCD,
∴AD⊥底面AEB,BC⊥底面AEB.
∴BE⊥AD,又AD∩AE=A,AD,AE 平面ADE,
∴BE⊥平面ADE,∴BE⊥DE.
同理可得,AE⊥CE,易得平面BCE⊥平面ADE.
可得A,B,D正确.
∵AD∥BC,∴∠ADE(或其补角)为DE与CB所成的角,显然∠ADE≠90°,∴DE⊥平面CEB不成立,即C错误.
10.ABD 连接BD,图略,显然O为BD的中点,又N为PB的中点,所以PD∥ON,由线面平行的判定定理可得,PD∥平面OMN,A正确;
由M,N分别为侧棱PA,PB的中点,所以MN∥AB,又底面为正方形,所以AB∥CD,所以MN∥CD,由线面平行的判定定理可得,CD∥平面OMN,又由选项A得PD∥平面OMN,由面面平行的判定定理可得,平面PCD∥平面OMN,B正确;
因为MN∥CD,所以∠PDC为直线PD与直线MN所成的角,又因为所有棱长都相等,所以∠PDC=60°,故直线PD与直线MN所成角的大小为60°,C错误;
因为底面为正方形,所以AB2+AD2=BD2,又所有棱长都相等,所以PB2+PD2=BD2,故PB⊥PD,
又PD∥ON,所以ON⊥PB,D正确.
11.BC ∵AD1∥EF,
∴平面AEF即平面AEFD1,故A错误.
∵A1G∥D1F,A1G AEFD1,
∴A1G∥平面AEFD1,即A1G∥平面AEF,故B正确.
平面AEF截正方体所得截面为等腰梯形AEFD1,易知梯形面积为,故C正确.
点G到平面AEFM的距离即点A1到面AD1F的距离,显然D错误.
12.5 200π 设圆柱的底面圆的半径为r cm,
则S圆柱表=2π·r·8+2πr2=130π.解得r=5,即圆柱的底面圆半径为5 cm.圆柱的体积V=52π×8=200π(cm3).
13. 正三棱柱ABC-A'B'C'的侧面部分展开图如图所示,
图1
图2
如图1,连接AC'与BB'交于点G,则爬行的最短路程是沿着AC'爬行,
此时AC'==4.
如图2,连接AC',过C'作AB的垂线交A'B'于点E,则C'E=A'C'·sin 60°=,则C'F=,所以AC'=.
<4,∴爬行的最短路程是.
14. 设AC∩BD=O,则翻折后AO⊥BD,CO⊥BD,即∠AOC即为二面角的平面角,所以∠AOC=120°,且AO=1,故d=1×sin 60°=.
15.解(1)设圆锥的底面半径为r,母线长为l,高为h1,圆柱高为h2,
则由题意有2πr=24π,得r=12 cm,圆锥高h1==16(cm),
所以“笼具”的体积V=πr2h2+r2h1=π144×30+144×16=5 088π≈15 976.3(cm3).
(2)圆柱的侧面积S1=2πrh2=720π(cm2),圆柱的底面积S2=πr2=144π(cm2),
圆锥的侧面积S3=πrl=240π(cm2),
所以“笼具”的侧面积S侧=S1+S2+S3=1 104π(cm2).
故造50个“笼具”的保护罩的最低总造价为≈138.7(元).
16.(1)证明∵四边形ABCD为正方形,F为AC与BD的交点,∴F是BD的中点,
又E是PB的中点,∴EF∥PD.
又EF 平面PCD,PD 平面PCD,
∴EF∥平面PCD.
(2)解∵PA⊥平面ABCD,E是PB的中点,
∴点E到平面ABCD的距离d=PA=1.
∵四边形ABCD是正方形,AD=2,
∴S△ABF=S正方形ABCD=1,
∴三棱锥E-ABF的体积V=S△ABF·d=1×1=.
17.
证明(1)取AB中点P,连接MP,PB1,
则MP∥BC,MP=BC.
又N是B1C1的中点,所以B1N=B1C1.
因为BC∥B1C1,BC=B1C1,所以MP∥B1N,MP=B1N.
所以四边形MPB1N是平行四边形,所以MN∥PB1.
因为MN 平面ABB1A1,PB1 平面ABB1A1,所以MN∥平面ABB1A1.
(2)连接AC1,A1C,BC1,B1C,如图,直三棱柱ABC-A1B1C1中,则BC⊥CC1,而AC⊥BC,则有BC⊥平面CC1A1A,必有BC⊥AC1,又由AC=CC1=1,四边形ACC1A1为正方形,则AC1⊥A1C,BC 平面A1BC,A1C 平面A1BC,BC∩A1C=C,则AC1⊥平面A1BC,必有AC1⊥A1B.
又由M,Q分别为AC,CC1的中点,则MQ∥AC1,
则有MQ⊥A1B.同理,NQ⊥A1B,
而MQ 平面MNQ,NQ 平面MNQ,MQ∩NQ=Q,
故有A1B⊥平面MNQ.
18.(1)解∵△PAD是边长为2的正三角形,N为AD的中点,∴PN⊥AD,PN=.
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PN 平面PAD,∴PN⊥平面ABCD.
又NC 平面ABCD,∴PN⊥NC.
∴∠DNC为二面角D-PN-C的平面角,
∴tan∠DNC=2=.
又DN=1,∴DC=2,
∴底面ABCD为正方形.
∴四棱锥P-ABCD的体积V=2×2.
(2)证明由(1)知,PN⊥平面ABCD,DM 平面ABCD,
∴PN⊥DM.
在正方形ABCD中,易知△DAM≌△CDN,∴∠ADM=∠DCN,
而∠ADM+∠MDC=90°,∴∠DCN+∠MDC=90°,
∴DM⊥CN.
∵PN∩CN=N,PN,CN 平面PNC,∴DM⊥平面PNC.
∵PC 平面PNC,
∴DM⊥PC.
(3)解设DM∩CN=O,连接PO,MN.
∵DM⊥平面PNC,
∴∠MPO为直线PM与平面PNC所成的角.
∵AD=2,AM=1,∴DM=,DO=,
∴MO=.
又MN=,PM=,
∴sin∠MPO=,
∴直线PM与平面PNC所成角的正弦值为.
19.(1)证明在题图2中,因为E,F分别是AC和BC的中点,所以EF∥AB.
因为AB 平面DEF,EF 平面DEF,所以AB∥平面DEF.
(2)解如图,在线段BC上取点P,使BP=BC,过点P在平面BCD内作PQ⊥CD于点Q,连接AQ.
由题意得,平面ACD⊥平面BCD.
因为PQ⊥CD,平面ACD∩平面BCD=CD,PQ 平面BCD,
所以PQ⊥平面ACD.
因为DE 平面ACD,所以PQ⊥DE.
在△BCD中,因为PQ⊥CD,且易知BD⊥CD,所以PQ∥BD,所以.
因为CD⊥AD,∠DAC=60°,所以CD=ADtan 60°=AD,故DQ=DC=AD.
在Rt△ADQ中,tan∠DAQ=,因为0°<∠DAQ<90°,则∠DAQ=30°.
又∠CAD=60°,所以AQ平分∠CAD.
因为DE是Rt△ACD斜边上的中线,则DE=AC=AE,且∠CAD=60°,
所以△ADE是等边三角形,则AQ⊥DE.
又因为PQ∩AQ=Q,PQ,AQ 平面APQ,所以DE⊥平面APQ.
因为AP 平面APQ,
所以AP⊥DE.
综上,在线段BC上存在一点P,且当时,AP⊥DE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版数学必修第二册
综合训练
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.[2024安徽合肥高一期末]如图,△A'B'C'是用斜二测画法画出的水平放置的△ABC的直观图,其中B'C'=C'A'=1,A'B'∥x'轴,A'C'∥y'轴,则BC=( )
A. B.2 C. D.4
2.某圆锥高为,母线与底面所成的角为,则该圆锥的表面积为( )
A.3π B.4π
C.5π D.6π
3.[2024山西太原高一期末]已知m,n是两条不同的直线,α,β是两个不重合的平面,则下列命题正确的是( )
A.若m∥n,m∥α,n∥β,则α∥β
B.若α∥β,m∥α,n β,则m∥n
C.若m⊥n,m⊥α,n⊥β,则α⊥β
D.若α⊥β,m∥α,n∥β,则m⊥n
4.在等腰直角三角形ABC中,AB=BC=1,M为AC的中点,沿BM把它折成二面角,折后点A与点C的距离为1,则二面角C-BM-A的大小为( )
A.30° B.60°
C.90° D.120°
5.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,则四边形ABCD绕AD所在直线旋转一周所成几何体的表面积为( )
A.(60+4)π B.(60+8)π
C.(56+8)π D.(56+4)π
6.在空间四边形ABCD中,AD=2,BC=2,E,F分别是AB,CD的中点,EF=,则异面直线AD与BC所成角的大小为( )
A.150° B.60°
C.120° D.30°
7.如图,正方体ABCD-A1B1C1D1的棱长为1,动点E在线段A1C1上,F,M分别是AD,CD的中点,则下列结论错误的是( )
A.FM∥A1C1
B.当E为A1C1中点时,BE⊥FM
C.三棱锥B-CEF的体积为定值
D.存在点E,使得平面BEF∥平面CC1D1D
8.已知三棱锥P-ABC的高为1,底面三角形ABC为等边三角形,PA=PB=PC,且P,A,B,C都在体积为的球O的表面上,则该三棱锥的底面三角形ABC的边长为( )
A. B.
C.3 D.2
二、选择题:在每小题给出的选项中,有多项符合题目要求.
9.如图,圆柱的轴截面是四边形ABCD,E是底面圆周上异于A,B的一点,则下列结论中正确的是( )
A.AE⊥CE
B.BE⊥DE
C.DE⊥平面CEB
D.平面ADE⊥平面BCE
10.如图,在棱长均相等的四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,下列结论正确的是( )
A.PD∥平面OMN
B.平面PCD∥平面OMN
C.直线PD与直线MN所成角的大小为90°
D.ON⊥PB
11.正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为BC,CC1,BB1的中点,则( )
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C与点G到平面AEF的距离相等
三、填空题
12.圆柱的高是8 cm,表面积是130π cm2,则它的底面圆的半径等于 cm,圆柱的体积是 cm3.
13.如图,正三棱柱ABC-A'B'C'的底面边长为,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C',若侧面AA'C'C紧贴墙面(不能通行),则爬行的最短路程是 .
14.已知在菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起使二面角A-BD-C为120°,则点A到△BCD所在平面的距离为 .
四、解答题:解答应写出文字说明、证明过程或演算步骤.
15.某种“笼具”由上、下两层组成,上层和下层分别是一个圆锥和一个圆柱,其中圆柱与圆锥的底面半径相等,如图所示,圆锥无底面,圆柱无上底面有下底面,内部镂空,已知圆锥的母线长为20 cm,圆柱高为30 cm,底面的周长为24π cm.
(1)求这种“笼具”的体积(π取3.14,结果精确到0.1 cm3);
(2)现要使用一种纱网材料制作这样“笼具”的保护罩(包括底面)50个,该保护罩紧贴包裹“笼具”,纱网材料(按实测面积计算)的造价为每平方米8元,共需多少元 (结果精确到0.1元)
16.[2024内蒙古包头高一月考]如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AD=2,E为PB的中点,F为AC与BD的交点.
(1)证明:EF∥平面PCD;
(2)求三棱锥E-ABF的体积.
17.如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=1,M,N,Q分别为AC,B1C1,CC1的中点.求证:
(1)MN∥平面ABB1A1;
(2)A1B⊥平面MNQ.
18.[2024河北沧州高一期末]如图,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面四边形ABCD为矩形,且平面PAD⊥平面ABCD,M,N分别为AB,AD的中点,二面角D-PN-C的正切值为2.
(1)求四棱锥P-ABCD的体积;
(2)证明:DM⊥PC;
(3)求直线PM与平面PNC所成角的正弦值.
19.[2024吉林长春高一检测]如图1,在等边三角形ABC中,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ACD沿CD翻折,使得平面ACD⊥平面BCD,如图2.
图1
图2
(1)求证:AB∥平面DEF.
(2)在线段BC上是否存在一点P,使AP⊥DE 若存在,求的值;若不存在,请说明理由.
第八章综合训练
1.C 在△A'B'C'中,B'C'=C'A'=1,∠B'A'C'=45°,
由余弦定理可得B'C'2=A'C'2+A'B'2-2A'C'·A'B'·cos 45°,
即A'B'2-A'B'=0,而A'B'>0,解得A'B'=.
由斜二测画法可知,在△ABC中,AB⊥AC,AB=A'B'=,AC=2C'A'=2,
故BC=.
故选C.
2.A 由圆锥高为,母线与底面所成的角为,得圆锥底面圆半径r==1,母线l==2,所以圆锥的表面积S=πr2+πrl=3π.
故选A.
3.C 对于A,若m∥n,m∥α,n∥β,当m,n都平行于α与β的交线时,满足条件,此时α与β相交,故A错误;
对于B,若α∥β,m∥α,n β,则m,n可能异面,故B错误;
对于C,若m⊥n,m⊥α,n⊥β,则α⊥β,故C正确;
对于D,若α⊥β,m∥α,n∥β,则m,n可能平行或异面,故D错误.
故选C.
4.C
如图,由A'B=BC=1,∠A'BC=90°知A'C=.
∵M为A'C的中点,∴MC=AM=,且CM⊥BM,AM⊥BM,
∴∠CMA为二面角C-BM-A的平面角.
∵AC=1,MC=MA=,∴∠CMA=90°,故选C.
5.
A 四边形ABCD绕AD所在直线旋转一周所成的几何体,如图.
S表面=S圆台下底面+S圆台侧面+S圆锥侧面=+π(r1+r2)l2+πr1l1=π×52+π×(2+5)×5+π×2×2=(60+4)π.故选A.
6.D
如图所示.设BD的中点为O,连接EO,FO,所以EO∥AD,FO∥BC,则∠EOF是AD,BC所成的角或其补角,
又EO=AD=1,FO=BC=,EF=,
根据余弦定理,得cos∠EOF==-,
所以∠EOF=150°,异面直线AD与BC所成的角为30°.
7.D 连接AC,在正方体ABCD-A1B1C1D1中,因为AA1=CC1且AA1∥CC1,
所以四边形AA1C1C为平行四边形,则AC∥A1C1.
因为F,M分别是AD,CD的中点,所以FM∥AC∥A1C1,故A正确;
连接BA1,在正方体ABCD-A1B1C1D1中,BA1=BC1,当E为A1C1的中点时,BE⊥A1C1,所以BE⊥FM,故B正确;
因为三棱锥B-CEF的体积即为三棱锥E-BCF的体积,在三棱锥E-BCF中,底面三角形BCF的面积为定值,棱锥的高等于AA1,为定值,三棱锥E-BCF的体积为定值,则三棱锥B-CEF的体积为定值,故C正确;
直线BF与平面CC1D1D有交点,所以不存在点E,使得平面BEF∥平面CC1D1D,故D错误.故选D.
8.C 设球O的半径为R,由球的体积为可得,R3=,解得R=2.
因为三棱锥P-ABC的高h为1,所以球心O在三棱锥外.
如图,设点O1为△ABC的外心,则OO1⊥平面ABC.
在Rt△AO1O中,由A=OA2-O,且OO1=R-h=1,得AO1=.
因为△ABC为等边三角形,所以AO1=AB·sin 60°=AB,所以AB=AO1=3.故选C.
9.ABD 由AB是底面圆的直径,得∠AEB=90°,即AE⊥EB.
∵圆柱的轴截面是四边形ABCD,
∴AD⊥底面AEB,BC⊥底面AEB.
∴BE⊥AD,又AD∩AE=A,AD,AE 平面ADE,
∴BE⊥平面ADE,∴BE⊥DE.
同理可得,AE⊥CE,易得平面BCE⊥平面ADE.
可得A,B,D正确.
∵AD∥BC,∴∠ADE(或其补角)为DE与CB所成的角,显然∠ADE≠90°,∴DE⊥平面CEB不成立,即C错误.
10.ABD 连接BD,图略,显然O为BD的中点,又N为PB的中点,所以PD∥ON,由线面平行的判定定理可得,PD∥平面OMN,A正确;
由M,N分别为侧棱PA,PB的中点,所以MN∥AB,又底面为正方形,所以AB∥CD,所以MN∥CD,由线面平行的判定定理可得,CD∥平面OMN,又由选项A得PD∥平面OMN,由面面平行的判定定理可得,平面PCD∥平面OMN,B正确;
因为MN∥CD,所以∠PDC为直线PD与直线MN所成的角,又因为所有棱长都相等,所以∠PDC=60°,故直线PD与直线MN所成角的大小为60°,C错误;
因为底面为正方形,所以AB2+AD2=BD2,又所有棱长都相等,所以PB2+PD2=BD2,故PB⊥PD,
又PD∥ON,所以ON⊥PB,D正确.
11.BC ∵AD1∥EF,
∴平面AEF即平面AEFD1,故A错误.
∵A1G∥D1F,A1G AEFD1,
∴A1G∥平面AEFD1,即A1G∥平面AEF,故B正确.
平面AEF截正方体所得截面为等腰梯形AEFD1,易知梯形面积为,故C正确.
点G到平面AEFM的距离即点A1到面AD1F的距离,显然D错误.
12.5 200π 设圆柱的底面圆的半径为r cm,
则S圆柱表=2π·r·8+2πr2=130π.解得r=5,即圆柱的底面圆半径为5 cm.圆柱的体积V=52π×8=200π(cm3).
13. 正三棱柱ABC-A'B'C'的侧面部分展开图如图所示,
图1
图2
如图1,连接AC'与BB'交于点G,则爬行的最短路程是沿着AC'爬行,
此时AC'==4.
如图2,连接AC',过C'作AB的垂线交A'B'于点E,则C'E=A'C'·sin 60°=,则C'F=,所以AC'=.
<4,∴爬行的最短路程是.
14. 设AC∩BD=O,则翻折后AO⊥BD,CO⊥BD,即∠AOC即为二面角的平面角,所以∠AOC=120°,且AO=1,故d=1×sin 60°=.
15.解(1)设圆锥的底面半径为r,母线长为l,高为h1,圆柱高为h2,
则由题意有2πr=24π,得r=12 cm,圆锥高h1==16(cm),
所以“笼具”的体积V=πr2h2+r2h1=π144×30+144×16=5 088π≈15 976.3(cm3).
(2)圆柱的侧面积S1=2πrh2=720π(cm2),圆柱的底面积S2=πr2=144π(cm2),
圆锥的侧面积S3=πrl=240π(cm2),
所以“笼具”的侧面积S侧=S1+S2+S3=1 104π(cm2).
故造50个“笼具”的保护罩的最低总造价为≈138.7(元).
16.(1)证明∵四边形ABCD为正方形,F为AC与BD的交点,∴F是BD的中点,
又E是PB的中点,∴EF∥PD.
又EF 平面PCD,PD 平面PCD,
∴EF∥平面PCD.
(2)解∵PA⊥平面ABCD,E是PB的中点,
∴点E到平面ABCD的距离d=PA=1.
∵四边形ABCD是正方形,AD=2,
∴S△ABF=S正方形ABCD=1,
∴三棱锥E-ABF的体积V=S△ABF·d=1×1=.
17.
证明(1)取AB中点P,连接MP,PB1,
则MP∥BC,MP=BC.
又N是B1C1的中点,所以B1N=B1C1.
因为BC∥B1C1,BC=B1C1,所以MP∥B1N,MP=B1N.
所以四边形MPB1N是平行四边形,所以MN∥PB1.
因为MN 平面ABB1A1,PB1 平面ABB1A1,所以MN∥平面ABB1A1.
(2)连接AC1,A1C,BC1,B1C,如图,直三棱柱ABC-A1B1C1中,则BC⊥CC1,而AC⊥BC,则有BC⊥平面CC1A1A,必有BC⊥AC1,又由AC=CC1=1,四边形ACC1A1为正方形,则AC1⊥A1C,BC 平面A1BC,A1C 平面A1BC,BC∩A1C=C,则AC1⊥平面A1BC,必有AC1⊥A1B.
又由M,Q分别为AC,CC1的中点,则MQ∥AC1,
则有MQ⊥A1B.同理,NQ⊥A1B,
而MQ 平面MNQ,NQ 平面MNQ,MQ∩NQ=Q,
故有A1B⊥平面MNQ.
18.(1)解∵△PAD是边长为2的正三角形,N为AD的中点,∴PN⊥AD,PN=.
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PN 平面PAD,∴PN⊥平面ABCD.
又NC 平面ABCD,∴PN⊥NC.
∴∠DNC为二面角D-PN-C的平面角,
∴tan∠DNC=2=.
又DN=1,∴DC=2,
∴底面ABCD为正方形.
∴四棱锥P-ABCD的体积V=2×2.
(2)证明由(1)知,PN⊥平面ABCD,DM 平面ABCD,
∴PN⊥DM.
在正方形ABCD中,易知△DAM≌△CDN,∴∠ADM=∠DCN,
而∠ADM+∠MDC=90°,∴∠DCN+∠MDC=90°,
∴DM⊥CN.
∵PN∩CN=N,PN,CN 平面PNC,∴DM⊥平面PNC.
∵PC 平面PNC,
∴DM⊥PC.
(3)解设DM∩CN=O,连接PO,MN.
∵DM⊥平面PNC,
∴∠MPO为直线PM与平面PNC所成的角.
∵AD=2,AM=1,∴DM=,DO=,
∴MO=.
又MN=,PM=,
∴sin∠MPO=,
∴直线PM与平面PNC所成角的正弦值为.
19.(1)证明在题图2中,因为E,F分别是AC和BC的中点,所以EF∥AB.
因为AB 平面DEF,EF 平面DEF,所以AB∥平面DEF.
(2)解如图,在线段BC上取点P,使BP=BC,过点P在平面BCD内作PQ⊥CD于点Q,连接AQ.
由题意得,平面ACD⊥平面BCD.
因为PQ⊥CD,平面ACD∩平面BCD=CD,PQ 平面BCD,
所以PQ⊥平面ACD.
因为DE 平面ACD,所以PQ⊥DE.
在△BCD中,因为PQ⊥CD,且易知BD⊥CD,所以PQ∥BD,所以.
因为CD⊥AD,∠DAC=60°,所以CD=ADtan 60°=AD,故DQ=DC=AD.
在Rt△ADQ中,tan∠DAQ=,因为0°<∠DAQ<90°,则∠DAQ=30°.
又∠CAD=60°,所以AQ平分∠CAD.
因为DE是Rt△ACD斜边上的中线,则DE=AC=AE,且∠CAD=60°,
所以△ADE是等边三角形,则AQ⊥DE.
又因为PQ∩AQ=Q,PQ,AQ 平面APQ,所以DE⊥平面APQ.
因为AP 平面APQ,
所以AP⊥DE.
综上,在线段BC上存在一点P,且当时,AP⊥DE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
