第9章测评--2025人教A版数学必修第二册同步练习题(含解析)
文档属性
| 名称 | 第9章测评--2025人教A版数学必修第二册同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 533.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教A版数学必修第二册
第九章测评
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列调查中属于抽样调查的是( )
①每隔5年进行一次人口普查;
②调查某商品的质量优劣;
③某报社对某个事情进行舆论调查;
④高考考生的身体检查.
A.②③ B.①④
C.③④ D.①②
2.在某种疫苗试验初期,某居民区有5 000人自愿接种了新冠疫苗,其中60~70岁的老年人有1 400人,16~19岁的中学生有400人,其余为符合接种条件的其他年龄段的居民.在一项接种疫苗的追踪调查中,要用分层随机抽样的方法从该居民区5 000名接种疫苗的人群中抽取部分人作为样本进行追踪调查,已知老年人中抽取了14人,则从其余符合接种条件的其他年龄段的居民中抽取的人数为( )
A.14 B.18
C.32 D.50
3.某中学国旗班共有50名学生,其中男女比例为3∶2,平均身高为174 cm,用分层随机抽样的方法从中抽取一个容量为20的样本,若样本中男生的平均身高为178 cm,则样本中女生人数与女生平均身高的估计值分别为( )
A.8人 168 cm B.8人 170 cm
C.12人 168 cm D.12人 170 cm
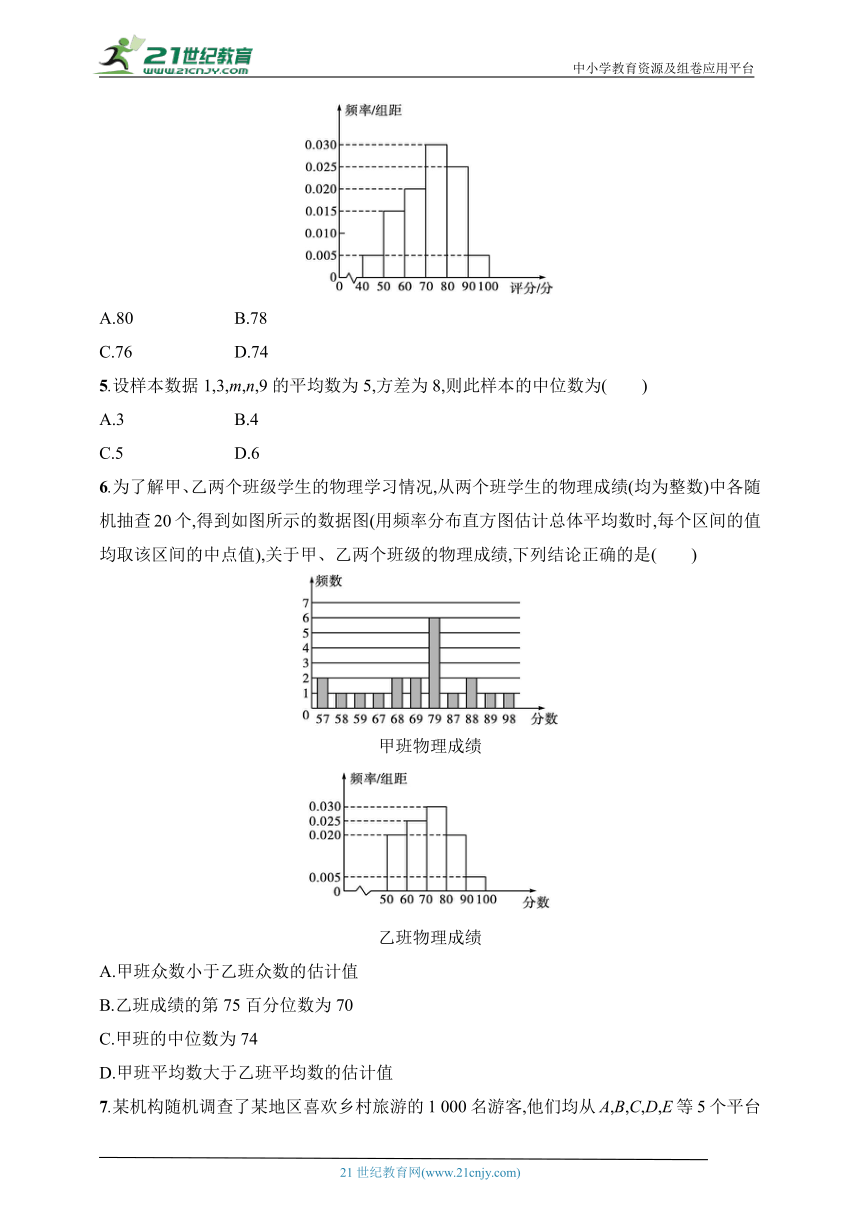
4.在一次学科核心素养能力测试活动中,随机抽取了100名同学的成绩(评分满分为100分),将所有数据按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,整理得到频率分布直方图如图所示,则估计这次调查数据的第64百分位数为( )
A.80 B.78
C.76 D.74
5.设样本数据1,3,m,n,9的平均数为5,方差为8,则此样本的中位数为( )
A.3 B.4
C.5 D.6
6.为了解甲、乙两个班级学生的物理学习情况,从两个班学生的物理成绩(均为整数)中各随机抽查20个,得到如图所示的数据图(用频率分布直方图估计总体平均数时,每个区间的值均取该区间的中点值),关于甲、乙两个班级的物理成绩,下列结论正确的是( )
甲班物理成绩
乙班物理成绩
A.甲班众数小于乙班众数的估计值
B.乙班成绩的第75百分位数为70
C.甲班的中位数为74
D.甲班平均数大于乙班平均数的估计值
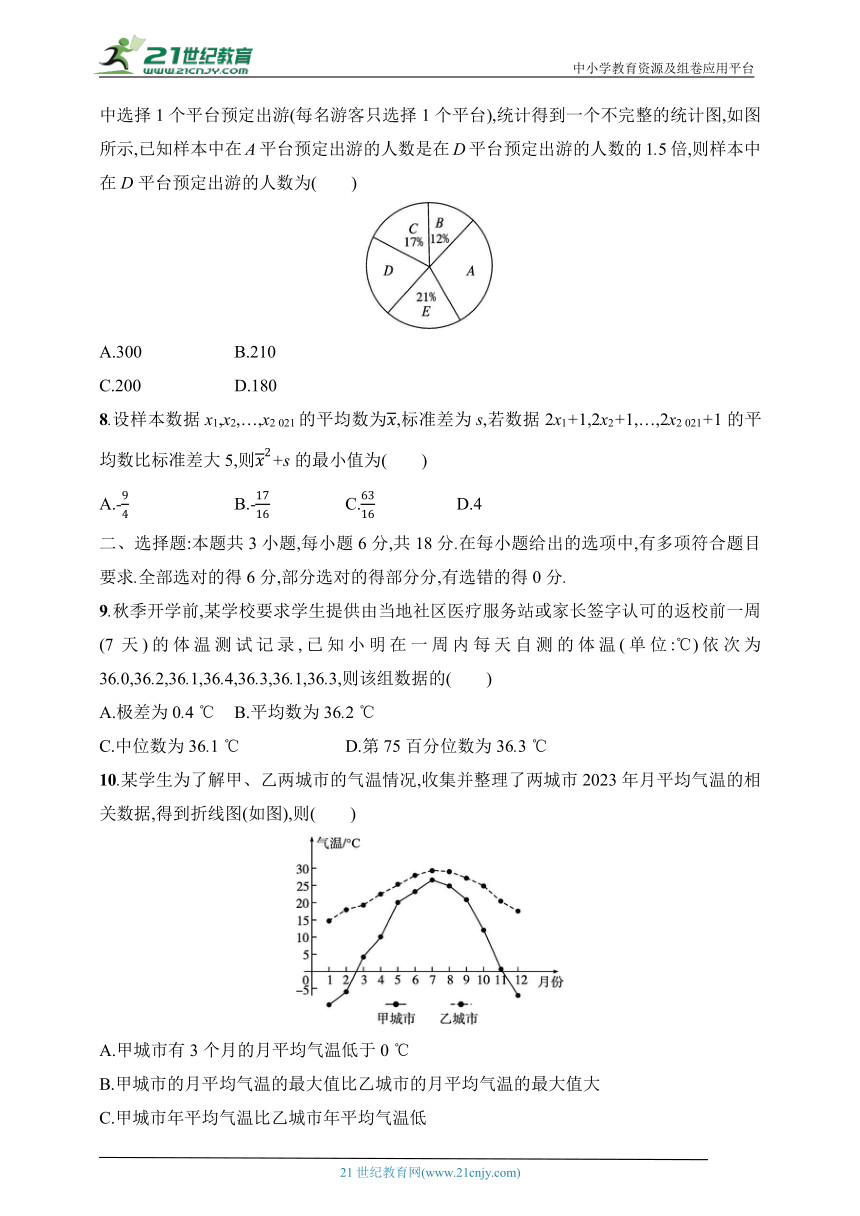
7.某机构随机调查了某地区喜欢乡村旅游的1 000名游客,他们均从A,B,C,D,E等5个平台中选择1个平台预定出游(每名游客只选择1个平台),统计得到一个不完整的统计图,如图所示,已知样本中在A平台预定出游的人数是在D平台预定出游的人数的1.5倍,则样本中在D平台预定出游的人数为( )
A.300 B.210
C.200 D.180
8.设样本数据x1,x2,…,x2 021的平均数为,标准差为s,若数据2x1+1,2x2+1,…,2x2 021+1的平均数比标准差大5,则+s的最小值为( )
A.- B.- C. D.4
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.秋季开学前,某学校要求学生提供由当地社区医疗服务站或家长签字认可的返校前一周(7天)的体温测试记录,已知小明在一周内每天自测的体温(单位:℃)依次为36.0,36.2,36.1,36.4,36.3,36.1,36.3,则该组数据的( )
A.极差为0.4 ℃ B.平均数为36.2 ℃
C.中位数为36.1 ℃ D.第75百分位数为36.3 ℃
10.某学生为了解甲、乙两城市的气温情况,收集并整理了两城市2023年月平均气温的相关数据,得到折线图(如图),则( )
A.甲城市有3个月的月平均气温低于0 ℃
B.甲城市的月平均气温的最大值比乙城市的月平均气温的最大值大
C.甲城市年平均气温比乙城市年平均气温低
D.甲城市月平均气温的方差比乙城市月平均气温的方差小
11.某学校利用学习强国APP安排教职工(共200人)在线学习党史知识.其教职工年龄情况和每周在线学习时长达3小时的情况分别如图①和图②所示,则下列说法正确的是( )
A.该学校中年教职工每周在线学习党史时长达3小时的人数最多
B.该学校老年教职工每周在线学习党史时长达3小时的人数最多
C.若要从该校的200名教职工中通过分层随机抽样的方法抽取20人,则应该从青年教职工中抽取6人
D.该学校在线学习党史时长达3小时的人数占总人数的80%
三、填空题:本题共3小题,每小题5分,共15分.
12.关于统计数据的分析,有以下几个结论:
①一组数不可能有两个众数;
②将一组数据中的每个数据都减去同一个数后,方差没有变化;
③调查剧院中观众观看感受时,从50排(每排人数相同)中任意抽取一排的人进行调查,属于分层随机抽样;
④一组数据的方差一定是正数.
其中结论错误的是 .
13.从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a= .若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层随机抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
14.如图是某高速公路测速点在2024年2月1日8:00到18:00内测得的过往车辆速度(单位:km/h)的频率分布直方图,则该段时间内过往车辆速度的中位数是 km/h,平均速度约为 km/h.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)某地准备修建一条新的地铁线路,为了调查市民对沿线地铁站配置方案的满意度,现对居民按年龄(单位:岁)进行问卷调查,从某小区年龄在[18,68]内的居民中随机抽取100人,将获得的数据按照年龄区间[18,28),[28,38),[38,48),[48,58),[58,68]分成5组,同时对这100人的意见情况进行统计得到频率分布表.经统计,在这100人中,共有65人赞同目前的地铁站配置方案.
分组 持赞同意见的人数 占本组的比例
[18,28) 20 0.8
[28,38) a b
[38,48) 8 0.8
[48,58) 12 0.6
[58,68] 15 0.6
(1)求a和b的值;
(2)在这100人中,按分层随机抽样的方法从年龄在区间[28,38),[38,48)内的居民(包括持反对意见者)中随机抽取18人进一步征询意见,求年龄在[28,38),[38,48)内的居民各抽取多少人
16.(15分)为调查高一、高二学生心理健康达标情况,某学校采用分层随机抽样方法,从高一、高二学生中分别抽取了50人、40人参加心理健康测试(满分:10分).经初步统计,参加测试的高一学生成绩xi(i=1,2,3,…,50)的平均分=7.4,方差=2.6,高二学生的成绩yi(i=1,2,3,…,40)的统计表如下:
成绩y 4 5 6 7 8 9
频数 3 7 11 9 6 4
(1)计算参加测试的高二学生成绩的平均分和方差;
(2)估计该学校高一、高二全体学生的平均分和方差.
17.(15分)某新能源汽车配件厂生产一种新能源汽车精密零件,为提高产品质量引入了一套新生产线,为检验新生产线所生产出来的零件质量有无显著提高,现同时用旧生产线和新生产线各生产了10个零件,得到各个零件的质量指标的数据如下:
旧生产线 5.2 4.8 4.8 5.0 5.0 5.2 5.1 4.8 5.1 5.0
新生产线 5.0 5.2 5.3 5.1 5.4 5.2 5.2 5.3 5.2 5.1
设旧生产线和新生产线所生产零件的质量指标的样本平均数分别为,样本方差分别为.
(1)求;
(2)若,则认为新生产线生产零件的质量有显著提高,否则不认为有显著提高,现计算得=0.022,试判断新生产线生产的零件质量较旧生产线生产的零件质量是否有显著提高.
18.(17分)自2004年以来,我国荒漠化和沙化状况呈现整体遏制、持续缩减、功能增强、成效明显的良好态势.治理沙漠离不开优质的树苗,现从苗圃中随机地抽测了200株树苗的高度(单位:cm),得到如图频率分布直方图.
(1)求直方图中a的值及众数、中位数;
(2)若树高185 cm及以上是可以移栽的合格树苗,
①求合格树苗的平均高度(结果精确到个位);
②从样本中按分层随机抽样方法抽取20株树苗作进一步研究,不合格树苗、合格树苗分别应抽取多少株
19.(17分)据调查,某市政府为了鼓励居民节约用水,减少水资源的浪费,计划在本市试行居民生活用水定额管理,即确定一个合理的居民用水量标准x(单位:吨),月均用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解全市居民用水量分布情况,通过抽样,获得了n户居民某年的月均用水量(单位:吨),其中月均用水量在[9,12)内的居民户数为39,并将数据制成了如图所示的频率分布直方图.
(1)求a和n的值.
(2)若该市政府希望使80%的居民用户月均用水量不超过标准x吨,试估计x的值.
(3)在(2)的条件下,若实施阶梯水价,月用水量不超过x吨时,按3元/吨计算,超出x吨的部分,按5元/吨计算.现市政府考核指标要求所有居民的月用水费均不超过70元,则该市居民用户月均用水量最多为多少吨
第九章测评
1.A 对于①,每隔5年进行一次人口普查,是普查,不是抽样调查;对于②,调查某商品的质量优劣,可以对该商品的一部分抽样调查;对于③,某报社对某个事情进行舆论调查,调查的范围广,应采用抽样调查;对于④,高考考生的身体检查,是普查,不能用抽样调查.所以适合用抽样调查的是②③.
2.C 设从其余符合接种条件的其他年龄段的居民中抽取的人数为x,由分层随机抽样的性质,得,解得x=32,∴从其余符合接种条件的其他年龄段的居民中抽取的人数为32.
3.A 由题意可知,样本中男生人数为20=12,女生人数为8,则样本中女生的平均身高为=168.故选A.
4.B 由0.005×10+0.015×10+0.020×10=0.4,
0.005×10+0.015×10+0.020×10+0.030×10=0.7,
故这次调查数据的第64百分位数位于[70,80)之间,
设这次调查数据的第64百分位数为x,
则有,解得x=78.故选B.
5.C 由题意可得,(1+3+m+n+9)=5,s2=[(1-5)2+(3-5)2+(m-5)2+(n-5)2+(9-5)2]=8,整理可得解得
∴该样本数据为1,3,5,7,9,故中位数为5.
6.D 甲班众数为79,乙班众数约为75,选项A错误;
∵0.020×10+0.025×10+0.030×10=0.75,
∴乙班成绩的第75百分位数为80,选项B错误;
根据频数分布图知,甲班学生的物理成绩从小到大排序的第10、第11个数是79,79,故甲班的中位数为79,选项C错误;
甲班平均数为(57×2+58+59+67+68×2+69×2+79×6+87+88×2+89+98)=74.8,
乙班平均数估计值为(55×0.020+65×0.025+75×0.030+85×0.020+95×0.005)×10=71.5,
故甲班平均数大于乙班平均数的估计值,选项D正确.
7.C 样本中在A平台预定出游的人数是在D平台预定出游的人数的1.5倍,设样本中在D平台预定出游的人数为a,则a+1.5a+(17%+12%+21%)×1 000=1 000,解得a=200.
∴样本中在D平台预定出游的人数为200.
8.A 样本数据x1,x2,…,x2 021的平均数为,标准差为s,
∵数据2x1+1,2x2+1,…,2x2 021+1的平均数比标准差大5,
∴2+1-2s=5,∴s=-2,
-2=,
∴当=-时,+s的最小值为-.
9.ABD 体温从低到高依次为36.0,36.1,36.1,36.2,36.3,36.3,36.4,极差为36.4-36.0=0.4(℃),故A正确;
平均数为=36.2(℃),故B正确;
中位数为36.2 ℃,故C错误;
因为7×75%=5.25,所以体温的第75百分位数为从小到大排列的第6个数,是36.3 ℃,故D正确.
10.AC 由折线图可得,甲城市在1月,2月,12月的月平均气温低于0 ℃,故A选项正确;甲、乙城市都在7月取得月平均气温的最大值,甲城市的月平均气温的最大值比乙城市的月平均气温的最大值小,故B选项错误;由折线图可知,乙城市的月平均折线图均在甲城市的月平均折线图的上方,所以甲城市年平均气温比乙城市年平均气温低,故C选项正确;由折线图可知,甲城市月平均气温比乙城市月平均气温波动大,所以甲城市月平均气温的方差比乙城市月平均气温的方差大,故D选项错误.
11.ACD 由图形知,该学校老年教职工在线学习党史时长达3小时的人数是200×30%×90%=54,中年教职工在线学习党史时长达3小时的人数是200×(1-30%-30%)×80%=64,青年教职工在线学习党史时长达3小时的人数是200×30%×70%=42,所以该学校中年教职工每周在线学习党史时长达3小时的人数最多,选项A正确,B错误;要从该校的200名教职工中通过分层随机抽样的方法抽取20人,应该从青年教职工中抽取20×30%=6(人),选项C正确;计算该学校在线学习党史时长达3小时的人数占总人数的比例为30%×90%+40%×80%+30%×70%=80%,所以选项D正确.
12.①③④ ①一组数可能有两个众数,故错误;②将一组数据中的每个数据都减去同一个数后,波动幅度没变,所以方差没有变化,故正确;③调查剧院中观众观看感受时,从50排(每排人数相同)中任意抽取一排的人进行调查,属于简单随机抽样,故错误;④一组数据的方差不一定是正数,可以是0,故错误.
13.0.030 3 ∵5个矩形面积之和为1,
即(0.005+0.010+0.020+a+0.035)×10=1,
∴0.070×10+10a=1,∴a=0.030.
∵三组内学生数的频率分别为0.3,0.2,0.1,
∴三组内学生的人数分别为30,20,10.
因此从[140,150]内选取的人数为18=3.
14.102.5 102 根据频率分布直方图中数据落在各区间的频率和为1得(0.01+0.03+0.02+m)×10=1,解得m=0.04,
该段时间内过往车辆速度的中位数是100+10=102.5;
平均速度约为85×0.1+95×0.3+105×0.4+115×0.2=102.
15.解(1)由题意,得20+8+12+15+a=65,解得a=10,
又=100,解得b=0.5.
(2)年龄在区间[28,38),[38,48)内的居民(包括持反对意见者)分别有=20(人),=10(人),故随机抽取18人进一步征询意见,年龄在[28,38)内的居民抽取18=12(人),
年龄在[38,48)内的居民抽取18=6(人).
16.解(1)由题意可得,
=6.5,
[3×(4-6.5)2+7×(5-6.5)2+11×(6-6.5)2+9×(7-6.5)2+6×(8-6.5)2+4×(9-6.5)2]=1.95.
(2)由(1)可得,(50+40)=(50×7.4+40×6.5)=7,
[2.6+(7.4-7)2]+[1.95+(6.5-7)2]=.
17.解(1)由题意得(5.2+4.8+4.8+5.0+5.0+5.2+5.1+4.8+5.1+5.0)=5.0,
(5.0+5.2+5.3+5.1+5.4+5.2+5.2+5.3+5.2+5.1)=5.2,
(4×0.12+2×0.22)=0.012.
(2)由(1)可得=5.2-5.0=0.2=,
因为,所以,
故新生产线生产的零件质量较旧生产线生产的零件质量有显著提高.
18.解(1)由题意,得(0.001 5+0.011 0+0.022 5+0.030 0+a+0.008 0+0.002 0)×10=1,解得a=0.025.
众数为=190,
因为(0.001 5+0.011 0+0.022 5)×10=0.35<0.5,
设中位数为x,则(0.001 5+0.011 0+0.022 5)×10+(x-185)×0.03=0.5,解得x=190,所以中位数为190.
(2)①因为树苗高度185 cm及以上的频率为(0.030 0+0.025 0+0.008 0+0.002 0)×10=0.65,
所以合格树苗的平均高度为(0.3×190+0.25×200+0.08×210+0.02×220)÷0.65≈197(cm).
②样本中合格树苗的频率为0.65,
则不合格树苗的频率为1-0.65=0.35,
所以按分层随机抽样方法抽取20株树苗,不合格树苗应抽取20×0.35=7(株),合格树苗应抽取20×0.65=13(株).
19.解(1)∵(0.015+0.025+0.050+0.065+0.085+0.050+0.020+0.015+0.005+a)×3=1,
∴a=.
∵用水量在[9,12)的频率为0.065×3=0.195,∴n==200(户).
(2)∵(0.015+0.025+0.050+0.065+0.085)×3=0.72<0.8,
(0.015+0.025+0.050+0.065+0.085+0.050)×3=0.87>0.8,
∴x=15+3=16.6(吨).
(3)设该市居民用户月均用水量最多为m吨,因为16.6×3=49.8<70,所以m>16.6,
则16.6×3+(m-16.6)×5≤70,解得m≤20.64.
∴该市居民用户月均用水量最多为20.64吨.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版数学必修第二册
第九章测评
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列调查中属于抽样调查的是( )
①每隔5年进行一次人口普查;
②调查某商品的质量优劣;
③某报社对某个事情进行舆论调查;
④高考考生的身体检查.
A.②③ B.①④
C.③④ D.①②
2.在某种疫苗试验初期,某居民区有5 000人自愿接种了新冠疫苗,其中60~70岁的老年人有1 400人,16~19岁的中学生有400人,其余为符合接种条件的其他年龄段的居民.在一项接种疫苗的追踪调查中,要用分层随机抽样的方法从该居民区5 000名接种疫苗的人群中抽取部分人作为样本进行追踪调查,已知老年人中抽取了14人,则从其余符合接种条件的其他年龄段的居民中抽取的人数为( )
A.14 B.18
C.32 D.50
3.某中学国旗班共有50名学生,其中男女比例为3∶2,平均身高为174 cm,用分层随机抽样的方法从中抽取一个容量为20的样本,若样本中男生的平均身高为178 cm,则样本中女生人数与女生平均身高的估计值分别为( )
A.8人 168 cm B.8人 170 cm
C.12人 168 cm D.12人 170 cm
4.在一次学科核心素养能力测试活动中,随机抽取了100名同学的成绩(评分满分为100分),将所有数据按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,整理得到频率分布直方图如图所示,则估计这次调查数据的第64百分位数为( )
A.80 B.78
C.76 D.74
5.设样本数据1,3,m,n,9的平均数为5,方差为8,则此样本的中位数为( )
A.3 B.4
C.5 D.6
6.为了解甲、乙两个班级学生的物理学习情况,从两个班学生的物理成绩(均为整数)中各随机抽查20个,得到如图所示的数据图(用频率分布直方图估计总体平均数时,每个区间的值均取该区间的中点值),关于甲、乙两个班级的物理成绩,下列结论正确的是( )
甲班物理成绩
乙班物理成绩
A.甲班众数小于乙班众数的估计值
B.乙班成绩的第75百分位数为70
C.甲班的中位数为74
D.甲班平均数大于乙班平均数的估计值
7.某机构随机调查了某地区喜欢乡村旅游的1 000名游客,他们均从A,B,C,D,E等5个平台中选择1个平台预定出游(每名游客只选择1个平台),统计得到一个不完整的统计图,如图所示,已知样本中在A平台预定出游的人数是在D平台预定出游的人数的1.5倍,则样本中在D平台预定出游的人数为( )
A.300 B.210
C.200 D.180
8.设样本数据x1,x2,…,x2 021的平均数为,标准差为s,若数据2x1+1,2x2+1,…,2x2 021+1的平均数比标准差大5,则+s的最小值为( )
A.- B.- C. D.4
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.秋季开学前,某学校要求学生提供由当地社区医疗服务站或家长签字认可的返校前一周(7天)的体温测试记录,已知小明在一周内每天自测的体温(单位:℃)依次为36.0,36.2,36.1,36.4,36.3,36.1,36.3,则该组数据的( )
A.极差为0.4 ℃ B.平均数为36.2 ℃
C.中位数为36.1 ℃ D.第75百分位数为36.3 ℃
10.某学生为了解甲、乙两城市的气温情况,收集并整理了两城市2023年月平均气温的相关数据,得到折线图(如图),则( )
A.甲城市有3个月的月平均气温低于0 ℃
B.甲城市的月平均气温的最大值比乙城市的月平均气温的最大值大
C.甲城市年平均气温比乙城市年平均气温低
D.甲城市月平均气温的方差比乙城市月平均气温的方差小
11.某学校利用学习强国APP安排教职工(共200人)在线学习党史知识.其教职工年龄情况和每周在线学习时长达3小时的情况分别如图①和图②所示,则下列说法正确的是( )
A.该学校中年教职工每周在线学习党史时长达3小时的人数最多
B.该学校老年教职工每周在线学习党史时长达3小时的人数最多
C.若要从该校的200名教职工中通过分层随机抽样的方法抽取20人,则应该从青年教职工中抽取6人
D.该学校在线学习党史时长达3小时的人数占总人数的80%
三、填空题:本题共3小题,每小题5分,共15分.
12.关于统计数据的分析,有以下几个结论:
①一组数不可能有两个众数;
②将一组数据中的每个数据都减去同一个数后,方差没有变化;
③调查剧院中观众观看感受时,从50排(每排人数相同)中任意抽取一排的人进行调查,属于分层随机抽样;
④一组数据的方差一定是正数.
其中结论错误的是 .
13.从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).由图中数据可知a= .若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层随机抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
14.如图是某高速公路测速点在2024年2月1日8:00到18:00内测得的过往车辆速度(单位:km/h)的频率分布直方图,则该段时间内过往车辆速度的中位数是 km/h,平均速度约为 km/h.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)某地准备修建一条新的地铁线路,为了调查市民对沿线地铁站配置方案的满意度,现对居民按年龄(单位:岁)进行问卷调查,从某小区年龄在[18,68]内的居民中随机抽取100人,将获得的数据按照年龄区间[18,28),[28,38),[38,48),[48,58),[58,68]分成5组,同时对这100人的意见情况进行统计得到频率分布表.经统计,在这100人中,共有65人赞同目前的地铁站配置方案.
分组 持赞同意见的人数 占本组的比例
[18,28) 20 0.8
[28,38) a b
[38,48) 8 0.8
[48,58) 12 0.6
[58,68] 15 0.6
(1)求a和b的值;
(2)在这100人中,按分层随机抽样的方法从年龄在区间[28,38),[38,48)内的居民(包括持反对意见者)中随机抽取18人进一步征询意见,求年龄在[28,38),[38,48)内的居民各抽取多少人
16.(15分)为调查高一、高二学生心理健康达标情况,某学校采用分层随机抽样方法,从高一、高二学生中分别抽取了50人、40人参加心理健康测试(满分:10分).经初步统计,参加测试的高一学生成绩xi(i=1,2,3,…,50)的平均分=7.4,方差=2.6,高二学生的成绩yi(i=1,2,3,…,40)的统计表如下:
成绩y 4 5 6 7 8 9
频数 3 7 11 9 6 4
(1)计算参加测试的高二学生成绩的平均分和方差;
(2)估计该学校高一、高二全体学生的平均分和方差.
17.(15分)某新能源汽车配件厂生产一种新能源汽车精密零件,为提高产品质量引入了一套新生产线,为检验新生产线所生产出来的零件质量有无显著提高,现同时用旧生产线和新生产线各生产了10个零件,得到各个零件的质量指标的数据如下:
旧生产线 5.2 4.8 4.8 5.0 5.0 5.2 5.1 4.8 5.1 5.0
新生产线 5.0 5.2 5.3 5.1 5.4 5.2 5.2 5.3 5.2 5.1
设旧生产线和新生产线所生产零件的质量指标的样本平均数分别为,样本方差分别为.
(1)求;
(2)若,则认为新生产线生产零件的质量有显著提高,否则不认为有显著提高,现计算得=0.022,试判断新生产线生产的零件质量较旧生产线生产的零件质量是否有显著提高.
18.(17分)自2004年以来,我国荒漠化和沙化状况呈现整体遏制、持续缩减、功能增强、成效明显的良好态势.治理沙漠离不开优质的树苗,现从苗圃中随机地抽测了200株树苗的高度(单位:cm),得到如图频率分布直方图.
(1)求直方图中a的值及众数、中位数;
(2)若树高185 cm及以上是可以移栽的合格树苗,
①求合格树苗的平均高度(结果精确到个位);
②从样本中按分层随机抽样方法抽取20株树苗作进一步研究,不合格树苗、合格树苗分别应抽取多少株
19.(17分)据调查,某市政府为了鼓励居民节约用水,减少水资源的浪费,计划在本市试行居民生活用水定额管理,即确定一个合理的居民用水量标准x(单位:吨),月均用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解全市居民用水量分布情况,通过抽样,获得了n户居民某年的月均用水量(单位:吨),其中月均用水量在[9,12)内的居民户数为39,并将数据制成了如图所示的频率分布直方图.
(1)求a和n的值.
(2)若该市政府希望使80%的居民用户月均用水量不超过标准x吨,试估计x的值.
(3)在(2)的条件下,若实施阶梯水价,月用水量不超过x吨时,按3元/吨计算,超出x吨的部分,按5元/吨计算.现市政府考核指标要求所有居民的月用水费均不超过70元,则该市居民用户月均用水量最多为多少吨
第九章测评
1.A 对于①,每隔5年进行一次人口普查,是普查,不是抽样调查;对于②,调查某商品的质量优劣,可以对该商品的一部分抽样调查;对于③,某报社对某个事情进行舆论调查,调查的范围广,应采用抽样调查;对于④,高考考生的身体检查,是普查,不能用抽样调查.所以适合用抽样调查的是②③.
2.C 设从其余符合接种条件的其他年龄段的居民中抽取的人数为x,由分层随机抽样的性质,得,解得x=32,∴从其余符合接种条件的其他年龄段的居民中抽取的人数为32.
3.A 由题意可知,样本中男生人数为20=12,女生人数为8,则样本中女生的平均身高为=168.故选A.
4.B 由0.005×10+0.015×10+0.020×10=0.4,
0.005×10+0.015×10+0.020×10+0.030×10=0.7,
故这次调查数据的第64百分位数位于[70,80)之间,
设这次调查数据的第64百分位数为x,
则有,解得x=78.故选B.
5.C 由题意可得,(1+3+m+n+9)=5,s2=[(1-5)2+(3-5)2+(m-5)2+(n-5)2+(9-5)2]=8,整理可得解得
∴该样本数据为1,3,5,7,9,故中位数为5.
6.D 甲班众数为79,乙班众数约为75,选项A错误;
∵0.020×10+0.025×10+0.030×10=0.75,
∴乙班成绩的第75百分位数为80,选项B错误;
根据频数分布图知,甲班学生的物理成绩从小到大排序的第10、第11个数是79,79,故甲班的中位数为79,选项C错误;
甲班平均数为(57×2+58+59+67+68×2+69×2+79×6+87+88×2+89+98)=74.8,
乙班平均数估计值为(55×0.020+65×0.025+75×0.030+85×0.020+95×0.005)×10=71.5,
故甲班平均数大于乙班平均数的估计值,选项D正确.
7.C 样本中在A平台预定出游的人数是在D平台预定出游的人数的1.5倍,设样本中在D平台预定出游的人数为a,则a+1.5a+(17%+12%+21%)×1 000=1 000,解得a=200.
∴样本中在D平台预定出游的人数为200.
8.A 样本数据x1,x2,…,x2 021的平均数为,标准差为s,
∵数据2x1+1,2x2+1,…,2x2 021+1的平均数比标准差大5,
∴2+1-2s=5,∴s=-2,
-2=,
∴当=-时,+s的最小值为-.
9.ABD 体温从低到高依次为36.0,36.1,36.1,36.2,36.3,36.3,36.4,极差为36.4-36.0=0.4(℃),故A正确;
平均数为=36.2(℃),故B正确;
中位数为36.2 ℃,故C错误;
因为7×75%=5.25,所以体温的第75百分位数为从小到大排列的第6个数,是36.3 ℃,故D正确.
10.AC 由折线图可得,甲城市在1月,2月,12月的月平均气温低于0 ℃,故A选项正确;甲、乙城市都在7月取得月平均气温的最大值,甲城市的月平均气温的最大值比乙城市的月平均气温的最大值小,故B选项错误;由折线图可知,乙城市的月平均折线图均在甲城市的月平均折线图的上方,所以甲城市年平均气温比乙城市年平均气温低,故C选项正确;由折线图可知,甲城市月平均气温比乙城市月平均气温波动大,所以甲城市月平均气温的方差比乙城市月平均气温的方差大,故D选项错误.
11.ACD 由图形知,该学校老年教职工在线学习党史时长达3小时的人数是200×30%×90%=54,中年教职工在线学习党史时长达3小时的人数是200×(1-30%-30%)×80%=64,青年教职工在线学习党史时长达3小时的人数是200×30%×70%=42,所以该学校中年教职工每周在线学习党史时长达3小时的人数最多,选项A正确,B错误;要从该校的200名教职工中通过分层随机抽样的方法抽取20人,应该从青年教职工中抽取20×30%=6(人),选项C正确;计算该学校在线学习党史时长达3小时的人数占总人数的比例为30%×90%+40%×80%+30%×70%=80%,所以选项D正确.
12.①③④ ①一组数可能有两个众数,故错误;②将一组数据中的每个数据都减去同一个数后,波动幅度没变,所以方差没有变化,故正确;③调查剧院中观众观看感受时,从50排(每排人数相同)中任意抽取一排的人进行调查,属于简单随机抽样,故错误;④一组数据的方差不一定是正数,可以是0,故错误.
13.0.030 3 ∵5个矩形面积之和为1,
即(0.005+0.010+0.020+a+0.035)×10=1,
∴0.070×10+10a=1,∴a=0.030.
∵三组内学生数的频率分别为0.3,0.2,0.1,
∴三组内学生的人数分别为30,20,10.
因此从[140,150]内选取的人数为18=3.
14.102.5 102 根据频率分布直方图中数据落在各区间的频率和为1得(0.01+0.03+0.02+m)×10=1,解得m=0.04,
该段时间内过往车辆速度的中位数是100+10=102.5;
平均速度约为85×0.1+95×0.3+105×0.4+115×0.2=102.
15.解(1)由题意,得20+8+12+15+a=65,解得a=10,
又=100,解得b=0.5.
(2)年龄在区间[28,38),[38,48)内的居民(包括持反对意见者)分别有=20(人),=10(人),故随机抽取18人进一步征询意见,年龄在[28,38)内的居民抽取18=12(人),
年龄在[38,48)内的居民抽取18=6(人).
16.解(1)由题意可得,
=6.5,
[3×(4-6.5)2+7×(5-6.5)2+11×(6-6.5)2+9×(7-6.5)2+6×(8-6.5)2+4×(9-6.5)2]=1.95.
(2)由(1)可得,(50+40)=(50×7.4+40×6.5)=7,
[2.6+(7.4-7)2]+[1.95+(6.5-7)2]=.
17.解(1)由题意得(5.2+4.8+4.8+5.0+5.0+5.2+5.1+4.8+5.1+5.0)=5.0,
(5.0+5.2+5.3+5.1+5.4+5.2+5.2+5.3+5.2+5.1)=5.2,
(4×0.12+2×0.22)=0.012.
(2)由(1)可得=5.2-5.0=0.2=,
因为,所以,
故新生产线生产的零件质量较旧生产线生产的零件质量有显著提高.
18.解(1)由题意,得(0.001 5+0.011 0+0.022 5+0.030 0+a+0.008 0+0.002 0)×10=1,解得a=0.025.
众数为=190,
因为(0.001 5+0.011 0+0.022 5)×10=0.35<0.5,
设中位数为x,则(0.001 5+0.011 0+0.022 5)×10+(x-185)×0.03=0.5,解得x=190,所以中位数为190.
(2)①因为树苗高度185 cm及以上的频率为(0.030 0+0.025 0+0.008 0+0.002 0)×10=0.65,
所以合格树苗的平均高度为(0.3×190+0.25×200+0.08×210+0.02×220)÷0.65≈197(cm).
②样本中合格树苗的频率为0.65,
则不合格树苗的频率为1-0.65=0.35,
所以按分层随机抽样方法抽取20株树苗,不合格树苗应抽取20×0.35=7(株),合格树苗应抽取20×0.65=13(株).
19.解(1)∵(0.015+0.025+0.050+0.065+0.085+0.050+0.020+0.015+0.005+a)×3=1,
∴a=.
∵用水量在[9,12)的频率为0.065×3=0.195,∴n==200(户).
(2)∵(0.015+0.025+0.050+0.065+0.085)×3=0.72<0.8,
(0.015+0.025+0.050+0.065+0.085+0.050)×3=0.87>0.8,
∴x=15+3=16.6(吨).
(3)设该市居民用户月均用水量最多为m吨,因为16.6×3=49.8<70,所以m>16.6,
则16.6×3+(m-16.6)×5≤70,解得m≤20.64.
∴该市居民用户月均用水量最多为20.64吨.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
