3.1.2 第1课时 函数的表示法--2025人教A版数学必修第一册同步练习题(含解析)
文档属性
| 名称 | 3.1.2 第1课时 函数的表示法--2025人教A版数学必修第一册同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 11:24:48 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025人教A版数学必修第一册
3.1.2 函数的表示法
第1课时 函数的表示法
A级 必备知识基础练
1.[探究点二]已知f(x)是反比例函数,且f(-3)=-1,则f(x)的解析式为( )
A.f(x)=- B.f(x)=
C.f(x)=3x D.f(x)=-3x
2.[探究点一]已知函数f(x)由下表给出,则满足f(f(x))>f(3)的x的值为( )
x 1 2 3
f(x) 2 3 1
A.1或3 B.1或2
C.2 D.3
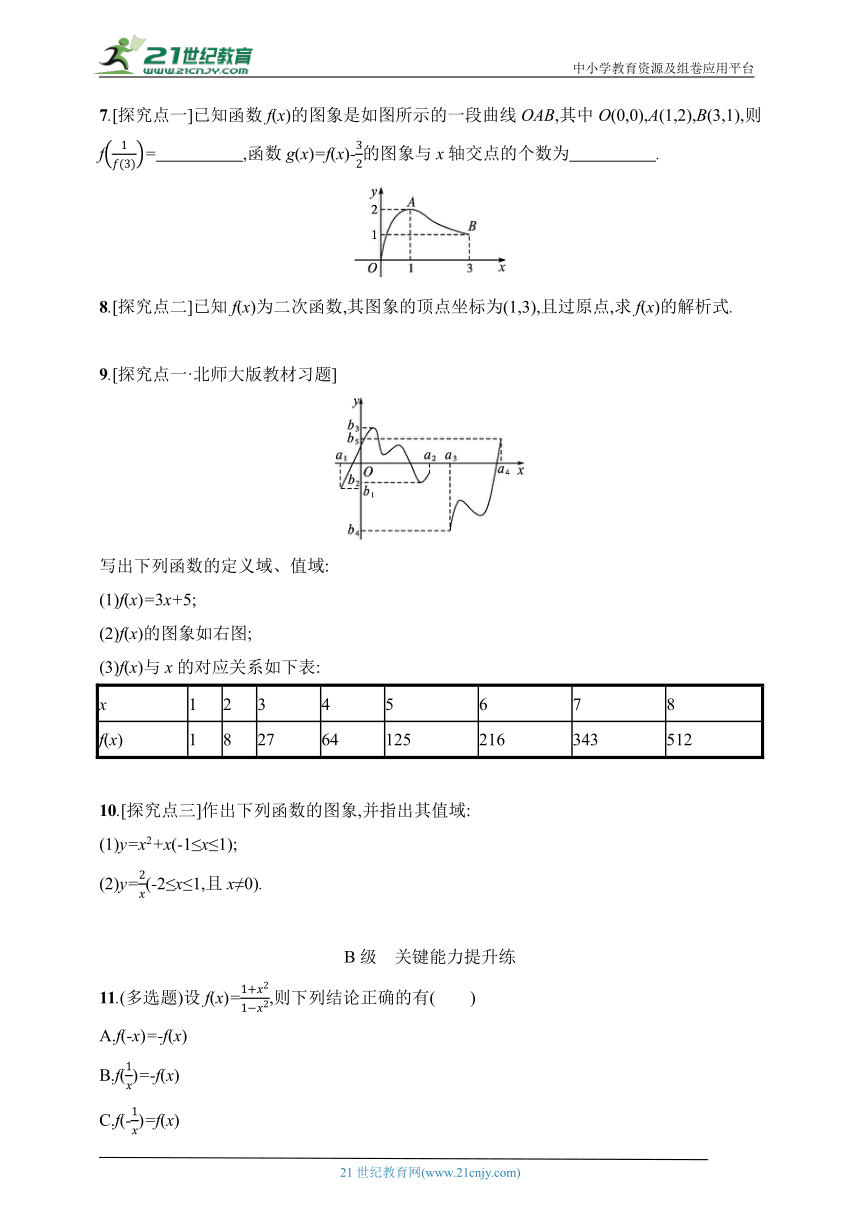
3.[探究点一]某同学到长城旅游,他租自行车由宾馆骑行前往长城,前进了a km,觉得有点累,休息后沿原路返回b km(b4.[探究点二]已知f=x,则f(x)=( )
A. B.
C. D.
5.[探究点二]已知f(x)是一次函数,且2f(2)-3f(1)=5,2f(0)-f(-1)=1,则f(x)=( )
A.3x+2 B.3x-2
C.2x+3 D.2x-3
6.[探究点二]已知f(x)是一次函数,若f(f(x))=4x+8,则f(x)的解析式为 .
7.[探究点一]已知函数f(x)的图象是如图所示的一段曲线OAB,其中O(0,0),A(1,2),B(3,1),则f= ,函数g(x)=f(x)-的图象与x轴交点的个数为 .
8.[探究点二]已知f(x)为二次函数,其图象的顶点坐标为(1,3),且过原点,求f(x)的解析式.
9.[探究点一·北师大版教材习题]
写出下列函数的定义域、值域:
(1)f(x)=3x+5;
(2)f(x)的图象如右图;
(3)f(x)与x的对应关系如下表:
x 1 2 3 4 5 6 7 8
f(x) 1 8 27 64 125 216 343 512
10.[探究点三]作出下列函数的图象,并指出其值域:
(1)y=x2+x(-1≤x≤1);
(2)y=(-2≤x≤1,且x≠0).
B级 关键能力提升练
11.(多选题)设f(x)=,则下列结论正确的有( )
A.f(-x)=-f(x)
B.f()=-f(x)
C.f(-)=f(x)
D.f(-x)=f(x)
12.若函数y=f(x)对任意x∈R,均有f(x+y)=f(x)+f(y),则下列函数中可以为y=f(x)解析式的是( )
A.f(x)=x+1 B.f(x)=2x-1
C.f(x)=2x D.f(x)=x2+x
13.(多选题)已知f(2x-1)=4x2,则下列结论正确的是( )
A.f(3)=9 B.f(-3)=4
C.f(x)=x2 D.f(x)=(x+1)2
14.已知f(+1)=,则f(x)= ,其定义域为 .
15.已知函数f(x)=.
(1)求f(2)与f(),f(3)与f().
(2)由(1)中求得结果,你能发现f(x)与f()有什么关系 并证明你的发现.
C级 学科素养创新练
16.(1)已知f(1+2x)=,求f(x)的解析式.
(2)已知g(x)-3g=x+2,求g(x)的解析式.
答案:
1.B 设f(x)=(k≠0),
∵f(-3)==-1,∴k=3,∴f(x)=.故选B.
2.A 由表知f(3)=1,若f(f(x))>f(3)=1,则f(x)=1或f(x)=2,所以x=3或x=1.故选A.
3.C 该同学先前进了a km,得图象是一段上升的直线,又休息了一段时间,图象是一段平行于t轴的直线,原路返回时,图象是一段下降的直线,调转车头继续前进时图象是一段上升的直线.故选C.
4.B 令=t,则t≠-1,x=,故f(t)=,即f(x)=.
5.B 设f(x)=kx+b(k≠0),
由题意可知
∴
∴∴f(x)=3x-2.故选B.
6.f(x)=2x+或f(x)=-2x-8 由题意可设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a2x+ab+b=4x+8.∴解得
∴f(x)=2x+或f(x)=-2x-8.
7.2 2 由题得f(3)=1,所以f()=f(1)=2.
令g(x)=f(x)-=0,所以f(x)=,观察函数f(x)的图象可以得到f(x)=有两个解,
所以g(x)=f(x)-的图象与x轴交点的个数为2.
8.解由于函数图象的顶点坐标为(1,3),且f(x)为二次函数,则设f(x)=a(x-1)2+3(a≠0).
∵函数图象过原点(0,0),∴a+3=0,∴a=-3.
故f(x)=-3(x-1)2+3.
9.解 (1)f(x)=3x+5的定义域为R,值域为R.
(2)f(x)的定义域为[a1,a2]∪[a3,a4],值域为[b4,b3].
(3)f(x)的定义域为{1,2,3,4,5,6,7,8},值域为{1,8,27,64,125,216,343,512}.
10.解(1)用描点法可以作出所求函数的图象如图所示.
由图可知y=x2+x(-1≤x≤1)的值域为.
(2)用描点法可以作出函数的图象如图所示.
由图可知y=(-2≤x≤1,且x≠0)的值域为(-∞,-1]∪[2,+∞).
11.BD 因为f(x)=,
所以f(-x)==f(x)≠-f(x),
f()==-f(x),f(-)==-f(x).故选BD.
12.C 若f(x)=2x,则f(x+y)=2(x+y),f(x)+f(y)=2x+2y=2(x+y),其他选项都不符合,故选C.
13.BD 令t=2x-1,则x=,
∴原函数化为f(t)=4=(t+1)2.
∴f(3)=16,f(-3)=4,f(x)=(x+1)2.
14.(x>1) (1,+∞) 令+1=t,由题意可知x>0,则t>1,x=(t-1)2,故f(t)=.
故f(x)=(x>1).
因此函数f(x)的定义域是(1,+∞).
15.解 (1)∵f(x)=,
∴f(2)=,f()=,f(3)=,f()=.
(2)由(1)发现f(x)+f()=1.
证明:
f(x)+f()==1.
16.解(1)由题意得,f(1+2x)的定义域为{x|x≠0}.
设t=1+2x(t≠1),则x=,∴f(t)=(t≠1),∴f(x)=(x≠1).
(2)由g(x)-3g=x+2,①
得g-3g(x)=+2,②
①②联立消去g得,g(x)=--1(x≠0).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版数学必修第一册
3.1.2 函数的表示法
第1课时 函数的表示法
A级 必备知识基础练
1.[探究点二]已知f(x)是反比例函数,且f(-3)=-1,则f(x)的解析式为( )
A.f(x)=- B.f(x)=
C.f(x)=3x D.f(x)=-3x
2.[探究点一]已知函数f(x)由下表给出,则满足f(f(x))>f(3)的x的值为( )
x 1 2 3
f(x) 2 3 1
A.1或3 B.1或2
C.2 D.3
3.[探究点一]某同学到长城旅游,他租自行车由宾馆骑行前往长城,前进了a km,觉得有点累,休息后沿原路返回b km(b
A. B.
C. D.
5.[探究点二]已知f(x)是一次函数,且2f(2)-3f(1)=5,2f(0)-f(-1)=1,则f(x)=( )
A.3x+2 B.3x-2
C.2x+3 D.2x-3
6.[探究点二]已知f(x)是一次函数,若f(f(x))=4x+8,则f(x)的解析式为 .
7.[探究点一]已知函数f(x)的图象是如图所示的一段曲线OAB,其中O(0,0),A(1,2),B(3,1),则f= ,函数g(x)=f(x)-的图象与x轴交点的个数为 .
8.[探究点二]已知f(x)为二次函数,其图象的顶点坐标为(1,3),且过原点,求f(x)的解析式.
9.[探究点一·北师大版教材习题]
写出下列函数的定义域、值域:
(1)f(x)=3x+5;
(2)f(x)的图象如右图;
(3)f(x)与x的对应关系如下表:
x 1 2 3 4 5 6 7 8
f(x) 1 8 27 64 125 216 343 512
10.[探究点三]作出下列函数的图象,并指出其值域:
(1)y=x2+x(-1≤x≤1);
(2)y=(-2≤x≤1,且x≠0).
B级 关键能力提升练
11.(多选题)设f(x)=,则下列结论正确的有( )
A.f(-x)=-f(x)
B.f()=-f(x)
C.f(-)=f(x)
D.f(-x)=f(x)
12.若函数y=f(x)对任意x∈R,均有f(x+y)=f(x)+f(y),则下列函数中可以为y=f(x)解析式的是( )
A.f(x)=x+1 B.f(x)=2x-1
C.f(x)=2x D.f(x)=x2+x
13.(多选题)已知f(2x-1)=4x2,则下列结论正确的是( )
A.f(3)=9 B.f(-3)=4
C.f(x)=x2 D.f(x)=(x+1)2
14.已知f(+1)=,则f(x)= ,其定义域为 .
15.已知函数f(x)=.
(1)求f(2)与f(),f(3)与f().
(2)由(1)中求得结果,你能发现f(x)与f()有什么关系 并证明你的发现.
C级 学科素养创新练
16.(1)已知f(1+2x)=,求f(x)的解析式.
(2)已知g(x)-3g=x+2,求g(x)的解析式.
答案:
1.B 设f(x)=(k≠0),
∵f(-3)==-1,∴k=3,∴f(x)=.故选B.
2.A 由表知f(3)=1,若f(f(x))>f(3)=1,则f(x)=1或f(x)=2,所以x=3或x=1.故选A.
3.C 该同学先前进了a km,得图象是一段上升的直线,又休息了一段时间,图象是一段平行于t轴的直线,原路返回时,图象是一段下降的直线,调转车头继续前进时图象是一段上升的直线.故选C.
4.B 令=t,则t≠-1,x=,故f(t)=,即f(x)=.
5.B 设f(x)=kx+b(k≠0),
由题意可知
∴
∴∴f(x)=3x-2.故选B.
6.f(x)=2x+或f(x)=-2x-8 由题意可设f(x)=ax+b(a≠0),
则f(f(x))=f(ax+b)=a2x+ab+b=4x+8.∴解得
∴f(x)=2x+或f(x)=-2x-8.
7.2 2 由题得f(3)=1,所以f()=f(1)=2.
令g(x)=f(x)-=0,所以f(x)=,观察函数f(x)的图象可以得到f(x)=有两个解,
所以g(x)=f(x)-的图象与x轴交点的个数为2.
8.解由于函数图象的顶点坐标为(1,3),且f(x)为二次函数,则设f(x)=a(x-1)2+3(a≠0).
∵函数图象过原点(0,0),∴a+3=0,∴a=-3.
故f(x)=-3(x-1)2+3.
9.解 (1)f(x)=3x+5的定义域为R,值域为R.
(2)f(x)的定义域为[a1,a2]∪[a3,a4],值域为[b4,b3].
(3)f(x)的定义域为{1,2,3,4,5,6,7,8},值域为{1,8,27,64,125,216,343,512}.
10.解(1)用描点法可以作出所求函数的图象如图所示.
由图可知y=x2+x(-1≤x≤1)的值域为.
(2)用描点法可以作出函数的图象如图所示.
由图可知y=(-2≤x≤1,且x≠0)的值域为(-∞,-1]∪[2,+∞).
11.BD 因为f(x)=,
所以f(-x)==f(x)≠-f(x),
f()==-f(x),f(-)==-f(x).故选BD.
12.C 若f(x)=2x,则f(x+y)=2(x+y),f(x)+f(y)=2x+2y=2(x+y),其他选项都不符合,故选C.
13.BD 令t=2x-1,则x=,
∴原函数化为f(t)=4=(t+1)2.
∴f(3)=16,f(-3)=4,f(x)=(x+1)2.
14.(x>1) (1,+∞) 令+1=t,由题意可知x>0,则t>1,x=(t-1)2,故f(t)=.
故f(x)=(x>1).
因此函数f(x)的定义域是(1,+∞).
15.解 (1)∵f(x)=,
∴f(2)=,f()=,f(3)=,f()=.
(2)由(1)发现f(x)+f()=1.
证明:
f(x)+f()==1.
16.解(1)由题意得,f(1+2x)的定义域为{x|x≠0}.
设t=1+2x(t≠1),则x=,∴f(t)=(t≠1),∴f(x)=(x≠1).
(2)由g(x)-3g=x+2,①
得g-3g(x)=+2,②
①②联立消去g得,g(x)=--1(x≠0).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
