4.4.1 对数函数的概念--4.4.2 对数函数的图象和性质--2025人教A版数学必修第一册同步练习题(含解析)
文档属性
| 名称 | 4.4.1 对数函数的概念--4.4.2 对数函数的图象和性质--2025人教A版数学必修第一册同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 375.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 11:01:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025人教A版数学必修第一册
4.4 对数函数
4.4.1 对数函数的概念
4.4.2 对数函数的图象和性质
A级 必备知识基础练
1.[探究点一](多选题)下列函数表达式中,是对数函数的有( )
A.y=logπx B.y=logx
C.y=log4x2 D.y=log2(x+1)
2.[探究点二]函数f(x)=的定义域为( )
A.(0,1) B.(1,+∞)
C.(0,+∞) D.(0,1)∪(1,+∞)
3.[探究点四]对数函数y=logax与y=logbx的图象如图,则( )
A.a<0,b<0
B.a<0,b>0
C.01
D.04.[探究点三]若函数y=f(x)是函数y=ax(a>0,且a≠1)的反函数,其图象经过点(,a),则f(x)=( )
A.log2x B.lox
C. D.x2
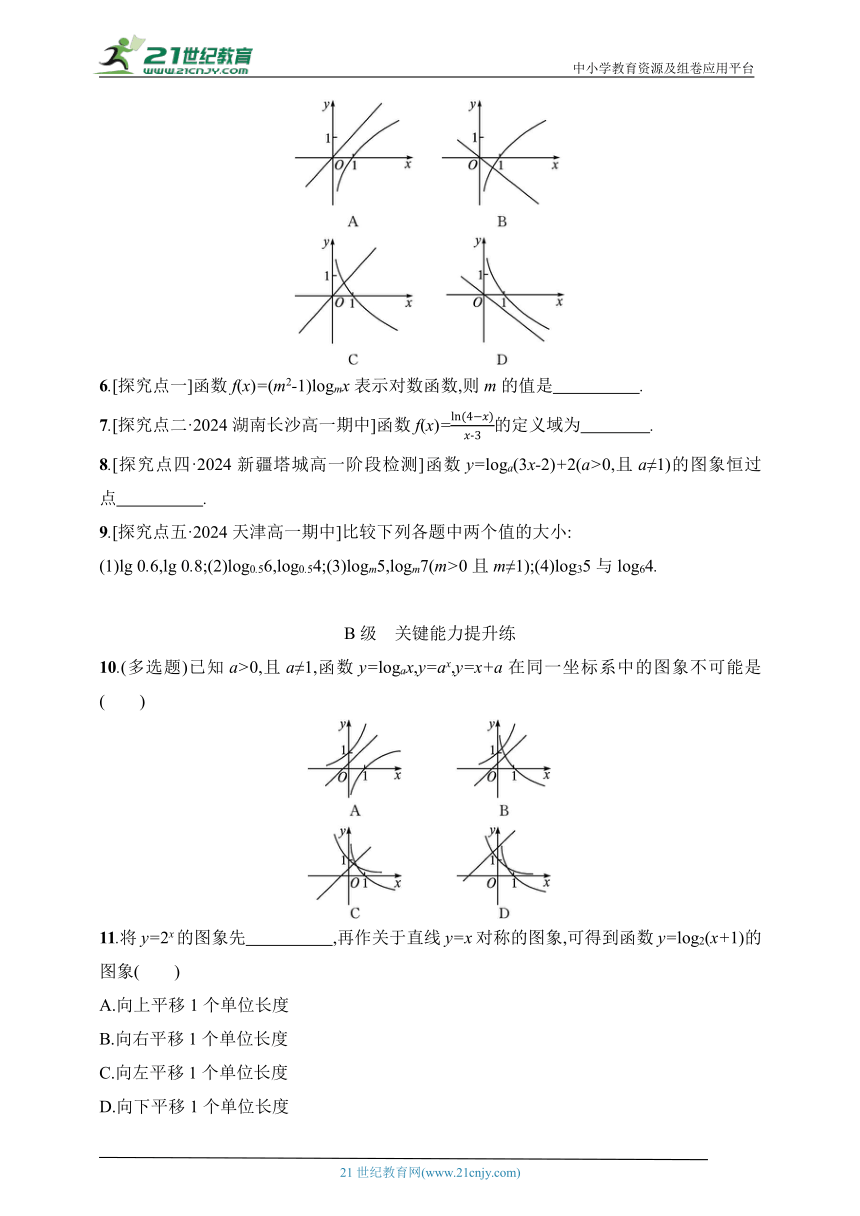
5.[探究点四]函数y=(1-a)x与y=logax(其中a>1)的图象只可能是( )
6.[探究点一]函数f(x)=(m2-1)logmx表示对数函数,则m的值是 .
7.[探究点二·2024湖南长沙高一期中]函数f(x)=的定义域为 .
8.[探究点四·2024新疆塔城高一阶段检测]函数y=loga(3x-2)+2(a>0,且a≠1)的图象恒过点 .
9.[探究点五·2024天津高一期中]比较下列各题中两个值的大小:
(1)lg 0.6,lg 0.8;(2)log0.56,log0.54;(3)logm5,logm7(m>0且m≠1);(4)log35与log64.
B级 关键能力提升练
10.(多选题)已知a>0,且a≠1,函数y=logax,y=ax,y=x+a在同一坐标系中的图象不可能是( )
11.将y=2x的图象先 ,再作关于直线y=x对称的图象,可得到函数y=log2(x+1)的图象( )
A.向上平移1个单位长度
B.向右平移1个单位长度
C.向左平移1个单位长度
D.向下平移1个单位长度
12.[2024湖南长沙高一阶段练习]若a=2 0230.2,b=log0.22 023,c=0.22 023,则( )
A.a>b>c
B.b>a>c
C.a>c>b
D.c>a>b
13.[2024北京高一期中]已知a=,b=log2,c=lo,则下列关系式中正确的是( )
A.c>a>b B.a>c>b
C.a>b>c D.c>b>a
14.若函数f(x)=log2|a+x|的图象不过第四象限,则实数a的取值范围为 .
15.已知函数f(x)=的最小值为-1,则a的取值范围是 .
16.已知函数f(x)=直线y=a与函数f(x)的图象恒有两个不同的交点,则a的取值范围是 .
17.已知实数a,b满足等式log2a=log3b,给出下列五个关系式:
①a>b>1;②b>a>1;③a其中可能正确的关系式是 .
18.设f(x)=ax(a>0,且a≠1),其图象经过点(),g(x)的图象与f(x)的图象关于直线y=x对称.
(1)若f(2m)=4,f(n)=25,求2m+n的值;
(2)若g(x)在区间[,c]上的值域为[a,b],且b-a=,求c的值.
C级 学科素养创新练
19.设函数f(x)=ln(ax2+2x+a)的定义域为M.
(1)若1∈M,2 M,求实数a的取值范围;
(2)若M=R,求实数a的取值范围.
答案:
1.AB 根据对数函数的定义知,y=logπx,y=lox是对数函数.故选AB.
2.D 因为f(x)=,所以解得x>0且x≠1,
所以f(x)的定义域为(0,1)∪(1,+∞).故选D.
3.C
4.B 因为y=ax的反函数为y=logax,又此函数图象经过点(,a),因此loga=a,解得a=,所以f(x)=lox.
5.B 对于A,B,因为a>1,故y=(1-a)x为R上的减函数,其图象应下降,y=logax为(0,+∞)上的增函数,故A错误,B正确;
对于C,D,当a>1时,y=logax为(0,+∞)上的增函数,故C,D错误.故选B.
6. 由函数f(x)=(m2-1)logmx表示对数函数,可得解得m=.
7.(-∞,3)∪(3,4) 要使函数f(x)=有意义,
只需解得x<4且x≠3,
所以函数的定义域为(-∞,3)∪(3,4).
8.(1,2) 令3x-2=1,即x=1,得y=loga1+2=2,
故y=loga(3x-2)+2(a>0,且a≠1)的图象恒过点(1,2).
9.解 (1)∵函数y=lg x是(0,+∞)上的增函数,0.6<0.8,∴lg 0.6(2)∵函数y=log0.5x是(0,+∞)上的减函数,6>4,
∴log0.56(3)当m>1时,函数y=logmx是(0,+∞)上的增函数.
∵5<7,∴logm5当0∵5<7,∴logm5>logm7.
(4)∵log35>log33=1,log64log64.
10.ABD
11.D y=log2(x+1)的反函数是y=2x-1,所以将y=2x的图象先向下平移1个单位长度,得y=2x-1.
12.C 因为a=2 0230.2>2 0230=1,所以a>1.
因为b=log0.22 023因为c=0.22 023<0.20=1,且c=0.22 023>0,
所以0c>b.故选C.
13.A 因为a=<20=1,所以0因为c=lo>lo=1,所以c>1.
因为b=log2所以b<0,故c>a>b.
故选A.
14.[1,+∞) 函数f(x)=log2|a+x|的图象关于直线x=-a对称,其定义域为{x|x≠-a},
作出函数f(x)=log2|a+x|的大致图象如图所示,由图可得,要使函数f(x)=log2|a+x|的图象不过第四象限,则解得a≥1,所以实数a的取值范围为[1,+∞).
15. ∵当x≥时,log2x≥log2=-1,
∴当f(x)的最小值为-1时,-+a≥-1,∴a≥-.
16.(0,1] 函数f(x)的图象如图所示,要使直线y=a与f(x)的图象有两个不同的交点,则017.②④⑤ 实数a,b满足等式log2a=log3b,即y=log2x在x=a处的函数值和y=log3x在x=b处的函数值相等,当a=b=1时,log2a=log3b=0,此时⑤成立;作直线y=1,由图象知,此时log2a=log3b=1,可得a=2,b=3,由此知②成立,①不成立;作出直线y=-1,由图象知,此时log2a=log3b=-1,可得a=,b=,由此知④成立,③不成立.综上知正确的关系式为②④⑤.
18.解(1)因为f(x)=ax(a>0,且a≠1)的图象经过点,所以,所以a=10,
所以f(x)=10x.
因为f(2m)=4,f(n)=25,所以102m=4,10n=25,
所以102m·10n=100,所以102m+n=102,所以2m+n=2.
(2)因为g(x)的图象与f(x)的图象关于直线y=x对称,所以g(x)=lg x(x>0),且为增函数,
所以g(x)在区间[,c]上的值域为[lg,lg c]=[a,b].因为b-a=,所以lg c-lg,
所以lg c=2,则c=100.
19.解由题意M={x|ax2+2x+a>0}.
(1)由1∈M,2 M可得
化简得解得-1所以a的取值范围为.
(2)由M=R可得ax2+2x+a>0恒成立.
当a=0时,不等式可化为2x>0,解得x>0,显然不符合题意;
当a≠0时,由二次函数的图象可知Δ=22-4×a×a<0,且a>0,即化简得解得a>1.
所以a的取值范围为(1,+∞).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版数学必修第一册
4.4 对数函数
4.4.1 对数函数的概念
4.4.2 对数函数的图象和性质
A级 必备知识基础练
1.[探究点一](多选题)下列函数表达式中,是对数函数的有( )
A.y=logπx B.y=logx
C.y=log4x2 D.y=log2(x+1)
2.[探究点二]函数f(x)=的定义域为( )
A.(0,1) B.(1,+∞)
C.(0,+∞) D.(0,1)∪(1,+∞)
3.[探究点四]对数函数y=logax与y=logbx的图象如图,则( )
A.a<0,b<0
B.a<0,b>0
C.0
D.0
A.log2x B.lox
C. D.x2
5.[探究点四]函数y=(1-a)x与y=logax(其中a>1)的图象只可能是( )
6.[探究点一]函数f(x)=(m2-1)logmx表示对数函数,则m的值是 .
7.[探究点二·2024湖南长沙高一期中]函数f(x)=的定义域为 .
8.[探究点四·2024新疆塔城高一阶段检测]函数y=loga(3x-2)+2(a>0,且a≠1)的图象恒过点 .
9.[探究点五·2024天津高一期中]比较下列各题中两个值的大小:
(1)lg 0.6,lg 0.8;(2)log0.56,log0.54;(3)logm5,logm7(m>0且m≠1);(4)log35与log64.
B级 关键能力提升练
10.(多选题)已知a>0,且a≠1,函数y=logax,y=ax,y=x+a在同一坐标系中的图象不可能是( )
11.将y=2x的图象先 ,再作关于直线y=x对称的图象,可得到函数y=log2(x+1)的图象( )
A.向上平移1个单位长度
B.向右平移1个单位长度
C.向左平移1个单位长度
D.向下平移1个单位长度
12.[2024湖南长沙高一阶段练习]若a=2 0230.2,b=log0.22 023,c=0.22 023,则( )
A.a>b>c
B.b>a>c
C.a>c>b
D.c>a>b
13.[2024北京高一期中]已知a=,b=log2,c=lo,则下列关系式中正确的是( )
A.c>a>b B.a>c>b
C.a>b>c D.c>b>a
14.若函数f(x)=log2|a+x|的图象不过第四象限,则实数a的取值范围为 .
15.已知函数f(x)=的最小值为-1,则a的取值范围是 .
16.已知函数f(x)=直线y=a与函数f(x)的图象恒有两个不同的交点,则a的取值范围是 .
17.已知实数a,b满足等式log2a=log3b,给出下列五个关系式:
①a>b>1;②b>a>1;③a
18.设f(x)=ax(a>0,且a≠1),其图象经过点(),g(x)的图象与f(x)的图象关于直线y=x对称.
(1)若f(2m)=4,f(n)=25,求2m+n的值;
(2)若g(x)在区间[,c]上的值域为[a,b],且b-a=,求c的值.
C级 学科素养创新练
19.设函数f(x)=ln(ax2+2x+a)的定义域为M.
(1)若1∈M,2 M,求实数a的取值范围;
(2)若M=R,求实数a的取值范围.
答案:
1.AB 根据对数函数的定义知,y=logπx,y=lox是对数函数.故选AB.
2.D 因为f(x)=,所以解得x>0且x≠1,
所以f(x)的定义域为(0,1)∪(1,+∞).故选D.
3.C
4.B 因为y=ax的反函数为y=logax,又此函数图象经过点(,a),因此loga=a,解得a=,所以f(x)=lox.
5.B 对于A,B,因为a>1,故y=(1-a)x为R上的减函数,其图象应下降,y=logax为(0,+∞)上的增函数,故A错误,B正确;
对于C,D,当a>1时,y=logax为(0,+∞)上的增函数,故C,D错误.故选B.
6. 由函数f(x)=(m2-1)logmx表示对数函数,可得解得m=.
7.(-∞,3)∪(3,4) 要使函数f(x)=有意义,
只需解得x<4且x≠3,
所以函数的定义域为(-∞,3)∪(3,4).
8.(1,2) 令3x-2=1,即x=1,得y=loga1+2=2,
故y=loga(3x-2)+2(a>0,且a≠1)的图象恒过点(1,2).
9.解 (1)∵函数y=lg x是(0,+∞)上的增函数,0.6<0.8,∴lg 0.6
∴log0.56
∵5<7,∴logm5
(4)∵log35>log33=1,log64
10.ABD
11.D y=log2(x+1)的反函数是y=2x-1,所以将y=2x的图象先向下平移1个单位长度,得y=2x-1.
12.C 因为a=2 0230.2>2 0230=1,所以a>1.
因为b=log0.22 023
所以0
13.A 因为a=<20=1,所以0
因为b=log2
故选A.
14.[1,+∞) 函数f(x)=log2|a+x|的图象关于直线x=-a对称,其定义域为{x|x≠-a},
作出函数f(x)=log2|a+x|的大致图象如图所示,由图可得,要使函数f(x)=log2|a+x|的图象不过第四象限,则解得a≥1,所以实数a的取值范围为[1,+∞).
15. ∵当x≥时,log2x≥log2=-1,
∴当f(x)的最小值为-1时,-+a≥-1,∴a≥-.
16.(0,1] 函数f(x)的图象如图所示,要使直线y=a与f(x)的图象有两个不同的交点,则0
18.解(1)因为f(x)=ax(a>0,且a≠1)的图象经过点,所以,所以a=10,
所以f(x)=10x.
因为f(2m)=4,f(n)=25,所以102m=4,10n=25,
所以102m·10n=100,所以102m+n=102,所以2m+n=2.
(2)因为g(x)的图象与f(x)的图象关于直线y=x对称,所以g(x)=lg x(x>0),且为增函数,
所以g(x)在区间[,c]上的值域为[lg,lg c]=[a,b].因为b-a=,所以lg c-lg,
所以lg c=2,则c=100.
19.解由题意M={x|ax2+2x+a>0}.
(1)由1∈M,2 M可得
化简得解得-1
(2)由M=R可得ax2+2x+a>0恒成立.
当a=0时,不等式可化为2x>0,解得x>0,显然不符合题意;
当a≠0时,由二次函数的图象可知Δ=22-4×a×a<0,且a>0,即化简得解得a>1.
所以a的取值范围为(1,+∞).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
