6.1 平面向量的概念--2025人教A版数学必修第二册同步练习题(含解析)
文档属性
| 名称 | 6.1 平面向量的概念--2025人教A版数学必修第二册同步练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 401.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教A版数学必修第二册
6.1 平面向量的概念
A级必备知识基础练
1.(多选题)[探究点一·2024山东菏泽高一期末]下列说法错误的是( )
A.向量就是有向线段
B.若e1,e2是单位向量,则|e1|=|e2|
C.||=||
D.若||>||,则
2.[探究点三]给出下列命题:①起点相同,方向相同的两个非零向量的终点相同;②起点相同的两个相等的非零向量的终点相同;③两个平行的非零向量的方向相同;④两个共线的非零向量的起点与终点一定共线.其中正确的是( )
A.①② B.②
C.②③ D.③④
3.[探究点二]若||=||且,则四边形ABCD的形状为( )
A.正方形 B.矩形
C.菱形 D.等腰梯形
4.(多选题)[探究点三]下列说法正确的是( )
A.若||=||且,则四边形ABCD是菱形
B.在平行四边形ABCD中,一定有
C.若a=b,b=c,则a=c
D.若a∥b,b∥c,则a∥c
5.(多选题)[探究点一]下列说法正确的是( )
A.向量不能比较大小,但向量的模能比较大小
B.|a|与|b|是否相等与a与b的方向无关
C.向量的模一定是正数
D.若向量与向量是共线向量,则A,B,C,D四点在一条直线上
6.[探究点二]在四边形ABCD中,,且是单位向量,则四边形ABCD是 .
7. [探究点三]如图所示,4×3的矩形(每个小方格的边长均为1),在起点和终点都在小方格的顶点处的向量中,试问:
(1)与相等的向量共有几个
(2)与平行且模为的向量共有几个
(3)与方向相同且模为3的向量共有几个
B级关键能力提升练
8.已知a为单位向量,下列说法正确的是( )
A.a的长度为一个单位长度
B.a与0不平行
C.与a共线的单位向量只有一个(不包括a本身)
D.a与0不是平行向量
9.已知四边形ABCD,下列说法正确的是( )
A.若,则四边形ABCD为平行四边形
B.若||=||,则四边形ABCD为矩形
C.若,且||=||,则四边形ABCD为矩形
D.若||=||,且,则四边形ABCD为梯形
10. (多选题)如图,在菱形ABCD中,∠DAB=120°,则以下说法正确的是( )
A.与相等的向量只有一个(不包括本身)
B.与的模相等的向量有9个(不包括本身)
C.的模为模的倍
D.不共线
11.给出下列四个条件:①a=b;②|a|=|b|;③a与b方向相反;④|a|=0或|b|=0.其中能使a∥b成立的条件是 .(填序号)
12.已知||=1,||=2,若∠ABC=90°,则||= .
13.有下列说法:
①若向量a与b满足a≠b,则a一定不与b共线;
②在同一平面中,若||=||=||≠0,则点B,C,D在以A为圆心,以||长为半径的圆上;
③在 ABCD中,一定有;
④共线向量是在一条直线上的向量.
其中所有正确的说法是 .(填序号)
14. 已知在四边形ABCD中,,且||=||,tan D=,判断四边形ABCD的形状.
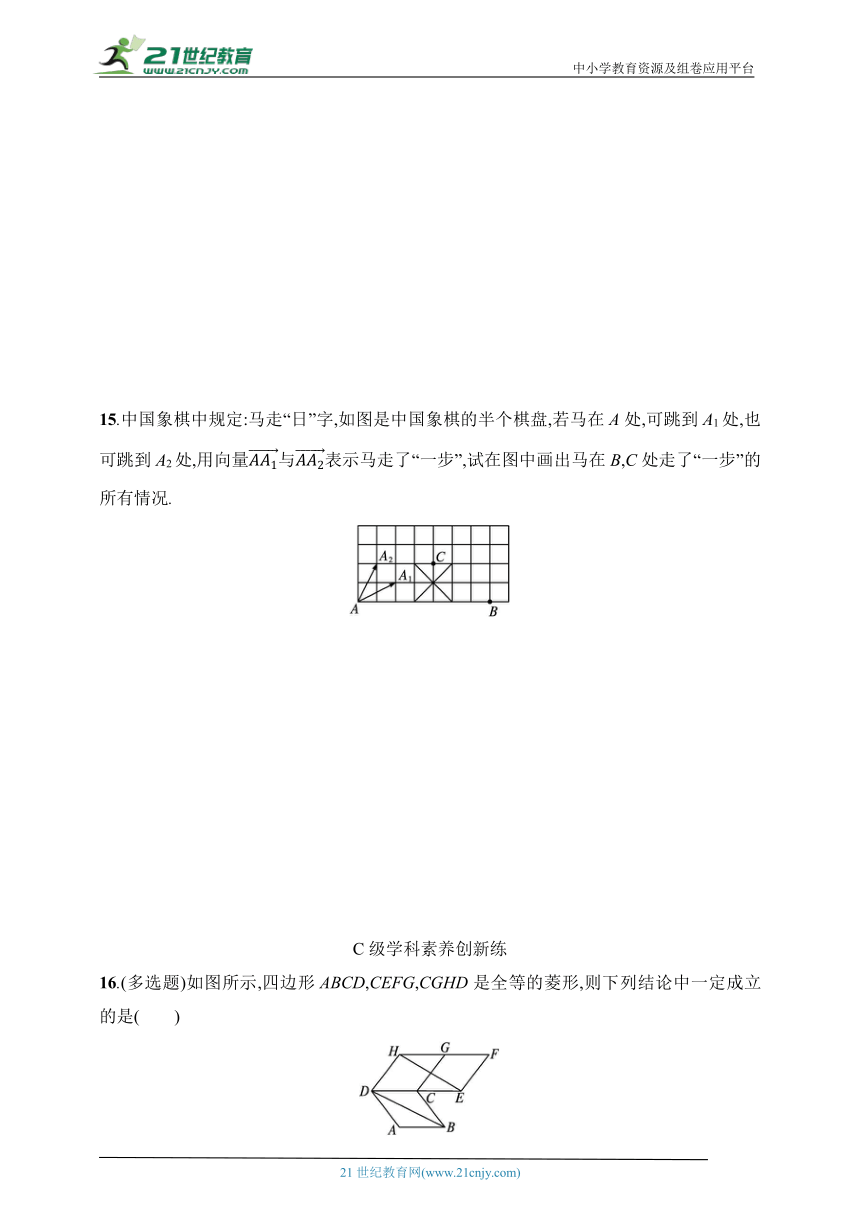
15.中国象棋中规定:马走“日”字,如图是中国象棋的半个棋盘,若马在A处,可跳到A1处,也可跳到A2处,用向量表示马走了“一步”,试在图中画出马在B,C处走了“一步”的所有情况.
C级学科素养创新练
16.(多选题)如图所示,四边形ABCD,CEFG,CGHD是全等的菱形,则下列结论中一定成立的是( )
A.||=||
B.共线
C.共线
D.
17.如图所示的方格纸由若干个边长为1的小正方形组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且||=.
(1)画出所有的向量;
(2)求||的最大值与最小值.
6.1 平面向量的概念
1.AD 向量可以用有向线段表示,但不能把两者等同,故A错误;由单位向量的定义可知,|e1|=|e2|,故B正确;因为CD=DC,所以||=||,故C正确;因为两个向量不能比较大小,故D错误.故选AD.
2.B ①起点相同,方向相同,但大小不一定相同,所以两个非零向量的终点不一定相同,故错误;
②起点相同的两个相等的非零向量的终点相同,故正确;
③两个平行的非零向量的方向相同或相反,故错误;
④两个共线的非零向量的起点与终点不一定共线,有向线段所在的直线可能平行,故错误.故选B.
3.C 由知,AB=CD且AB∥CD,即四边形ABCD为平行四边形.又因为||=||,所以四边形ABCD为菱形.
4.ABC 对于A,由,知AB=CD且AB∥CD,即四边形ABCD为平行四边形,又因为||=||,所以四边形ABCD为菱形,故A正确;对于B,在平行四边形ABCD中,对边平行且相等,的方向相同,所以,故B正确;对于C,由向量相等的定义知,当a=b,b=c时,有a=c,故C正确;对于D,当b=0时不成立,故D错误.故选ABC.
5.AB 对于A,向量既有大小又有方向,不能比较大小,向量的模可以比较大小,故选项A正确;对于B,|a|与|b|分别表示向量a与b的大小,与a,b的方向无关,故选项B正确;对于C,向量的模可能为零,故选项C不正确;对于D,若向量与向量是共线向量,表示的有向线段可能不在同一条直线上,得不出A,B,C,D四点在一条直线上,故选项D不正确.故选AB.
6.菱形 由可知四边形ABCD是平行四边形,
又是单位向量,所以||=||=1,所以四边形ABCD是菱形.
7.解(1)与向量相等的向量共有5个(不包括本身).
(2)与向量平行且模为的向量共有24个.
(3)与向量方向相同且模为3的向量共有2个.
8.A ∵已知a为单位向量,∴a的长度为一个单位长度,故A正确;
a与0平行,故B错误;
与a共线的单位向量有无数个,故C错误;零向量与任何向量都是平行向量,故D错误.
9.A A选项,若,则||=||且,则四边形ABCD为平行四边形,A正确;
B选项,如图,||=||=2,但是四边形ABCD不是矩形,B错误;
C选项,若,且||=||,则四边形ABCD可以是等腰梯形,也可以是矩形,故C错误;
D选项,若||=||,且,则四边形ABCD可以是平行四边形,也可以是梯形,D错误.故选A.
10.ABC A项,由相等向量的定义知,与相等的向量只有,故A正确;B项,因为AB=BC=CD=DA=AC,所以与的模相等的向量除外有9个,故B正确;C项,在Rt△ADO中,∠DAO=60°,则DO=DA,所以BD=DA,故C正确;D项,因为四边形ABCD是菱形,所以共线,故D错误.
11.①③④ 若a=b,则a与b大小相等且方向相同,所以a∥b;若|a|=|b|,则a与b的大小相等,而方向不确定,因此不一定有a∥b;方向相同或相反的向量都是平行向量,因此若a与b方向相反,则有a∥b;零向量与任意向量平行,所以若|a|=0或|b|=0,则a∥b.
12. 由勾股定理可知,|BC|=,即||=.
13.②③ ①两个向量不相等,可能是长度不相等,方向相同或相反,所以a与b有共线的可能,故①不正确;
②显然点B,C,D到点A的距离都等于||,故②正确;
③在平行四边形ABCD中,||=||,平行且方向相同,所以,故③正确;
④共线向量可以是在一条直线上的向量,也可以是所在直线互相平行的向量,故④不正确.
14.解∵在四边形ABCD中,,∴AB DC,
∴四边形ABCD是平行四边形.
∵tan D=,∴∠B=∠D=60°.
又||=||,
∴△ABC是等边三角形.
∴AB=BC,故四边形ABCD是菱形.
15.解根据规则,画出符合要求的所有向量,马在B处走了“一步”的情况如图所示,
马在C处走了“一步”的情况如图所示.
16.ABD 由向量相等及共线的概念,结合图形可知C不一定正确.
17.解(1)画出所有的向量如图所示.
(2)由(1)所画的图知,
①当点C位于点C1或C2时,||取得最小值;
②当点C位于点C5或C6时,||取得最大值.
∴||的最大值为,最小值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版数学必修第二册
6.1 平面向量的概念
A级必备知识基础练
1.(多选题)[探究点一·2024山东菏泽高一期末]下列说法错误的是( )
A.向量就是有向线段
B.若e1,e2是单位向量,则|e1|=|e2|
C.||=||
D.若||>||,则
2.[探究点三]给出下列命题:①起点相同,方向相同的两个非零向量的终点相同;②起点相同的两个相等的非零向量的终点相同;③两个平行的非零向量的方向相同;④两个共线的非零向量的起点与终点一定共线.其中正确的是( )
A.①② B.②
C.②③ D.③④
3.[探究点二]若||=||且,则四边形ABCD的形状为( )
A.正方形 B.矩形
C.菱形 D.等腰梯形
4.(多选题)[探究点三]下列说法正确的是( )
A.若||=||且,则四边形ABCD是菱形
B.在平行四边形ABCD中,一定有
C.若a=b,b=c,则a=c
D.若a∥b,b∥c,则a∥c
5.(多选题)[探究点一]下列说法正确的是( )
A.向量不能比较大小,但向量的模能比较大小
B.|a|与|b|是否相等与a与b的方向无关
C.向量的模一定是正数
D.若向量与向量是共线向量,则A,B,C,D四点在一条直线上
6.[探究点二]在四边形ABCD中,,且是单位向量,则四边形ABCD是 .
7. [探究点三]如图所示,4×3的矩形(每个小方格的边长均为1),在起点和终点都在小方格的顶点处的向量中,试问:
(1)与相等的向量共有几个
(2)与平行且模为的向量共有几个
(3)与方向相同且模为3的向量共有几个
B级关键能力提升练
8.已知a为单位向量,下列说法正确的是( )
A.a的长度为一个单位长度
B.a与0不平行
C.与a共线的单位向量只有一个(不包括a本身)
D.a与0不是平行向量
9.已知四边形ABCD,下列说法正确的是( )
A.若,则四边形ABCD为平行四边形
B.若||=||,则四边形ABCD为矩形
C.若,且||=||,则四边形ABCD为矩形
D.若||=||,且,则四边形ABCD为梯形
10. (多选题)如图,在菱形ABCD中,∠DAB=120°,则以下说法正确的是( )
A.与相等的向量只有一个(不包括本身)
B.与的模相等的向量有9个(不包括本身)
C.的模为模的倍
D.不共线
11.给出下列四个条件:①a=b;②|a|=|b|;③a与b方向相反;④|a|=0或|b|=0.其中能使a∥b成立的条件是 .(填序号)
12.已知||=1,||=2,若∠ABC=90°,则||= .
13.有下列说法:
①若向量a与b满足a≠b,则a一定不与b共线;
②在同一平面中,若||=||=||≠0,则点B,C,D在以A为圆心,以||长为半径的圆上;
③在 ABCD中,一定有;
④共线向量是在一条直线上的向量.
其中所有正确的说法是 .(填序号)
14. 已知在四边形ABCD中,,且||=||,tan D=,判断四边形ABCD的形状.
15.中国象棋中规定:马走“日”字,如图是中国象棋的半个棋盘,若马在A处,可跳到A1处,也可跳到A2处,用向量表示马走了“一步”,试在图中画出马在B,C处走了“一步”的所有情况.
C级学科素养创新练
16.(多选题)如图所示,四边形ABCD,CEFG,CGHD是全等的菱形,则下列结论中一定成立的是( )
A.||=||
B.共线
C.共线
D.
17.如图所示的方格纸由若干个边长为1的小正方形组成,方格纸中有两个定点A,B,点C为小正方形的顶点,且||=.
(1)画出所有的向量;
(2)求||的最大值与最小值.
6.1 平面向量的概念
1.AD 向量可以用有向线段表示,但不能把两者等同,故A错误;由单位向量的定义可知,|e1|=|e2|,故B正确;因为CD=DC,所以||=||,故C正确;因为两个向量不能比较大小,故D错误.故选AD.
2.B ①起点相同,方向相同,但大小不一定相同,所以两个非零向量的终点不一定相同,故错误;
②起点相同的两个相等的非零向量的终点相同,故正确;
③两个平行的非零向量的方向相同或相反,故错误;
④两个共线的非零向量的起点与终点不一定共线,有向线段所在的直线可能平行,故错误.故选B.
3.C 由知,AB=CD且AB∥CD,即四边形ABCD为平行四边形.又因为||=||,所以四边形ABCD为菱形.
4.ABC 对于A,由,知AB=CD且AB∥CD,即四边形ABCD为平行四边形,又因为||=||,所以四边形ABCD为菱形,故A正确;对于B,在平行四边形ABCD中,对边平行且相等,的方向相同,所以,故B正确;对于C,由向量相等的定义知,当a=b,b=c时,有a=c,故C正确;对于D,当b=0时不成立,故D错误.故选ABC.
5.AB 对于A,向量既有大小又有方向,不能比较大小,向量的模可以比较大小,故选项A正确;对于B,|a|与|b|分别表示向量a与b的大小,与a,b的方向无关,故选项B正确;对于C,向量的模可能为零,故选项C不正确;对于D,若向量与向量是共线向量,表示的有向线段可能不在同一条直线上,得不出A,B,C,D四点在一条直线上,故选项D不正确.故选AB.
6.菱形 由可知四边形ABCD是平行四边形,
又是单位向量,所以||=||=1,所以四边形ABCD是菱形.
7.解(1)与向量相等的向量共有5个(不包括本身).
(2)与向量平行且模为的向量共有24个.
(3)与向量方向相同且模为3的向量共有2个.
8.A ∵已知a为单位向量,∴a的长度为一个单位长度,故A正确;
a与0平行,故B错误;
与a共线的单位向量有无数个,故C错误;零向量与任何向量都是平行向量,故D错误.
9.A A选项,若,则||=||且,则四边形ABCD为平行四边形,A正确;
B选项,如图,||=||=2,但是四边形ABCD不是矩形,B错误;
C选项,若,且||=||,则四边形ABCD可以是等腰梯形,也可以是矩形,故C错误;
D选项,若||=||,且,则四边形ABCD可以是平行四边形,也可以是梯形,D错误.故选A.
10.ABC A项,由相等向量的定义知,与相等的向量只有,故A正确;B项,因为AB=BC=CD=DA=AC,所以与的模相等的向量除外有9个,故B正确;C项,在Rt△ADO中,∠DAO=60°,则DO=DA,所以BD=DA,故C正确;D项,因为四边形ABCD是菱形,所以共线,故D错误.
11.①③④ 若a=b,则a与b大小相等且方向相同,所以a∥b;若|a|=|b|,则a与b的大小相等,而方向不确定,因此不一定有a∥b;方向相同或相反的向量都是平行向量,因此若a与b方向相反,则有a∥b;零向量与任意向量平行,所以若|a|=0或|b|=0,则a∥b.
12. 由勾股定理可知,|BC|=,即||=.
13.②③ ①两个向量不相等,可能是长度不相等,方向相同或相反,所以a与b有共线的可能,故①不正确;
②显然点B,C,D到点A的距离都等于||,故②正确;
③在平行四边形ABCD中,||=||,平行且方向相同,所以,故③正确;
④共线向量可以是在一条直线上的向量,也可以是所在直线互相平行的向量,故④不正确.
14.解∵在四边形ABCD中,,∴AB DC,
∴四边形ABCD是平行四边形.
∵tan D=,∴∠B=∠D=60°.
又||=||,
∴△ABC是等边三角形.
∴AB=BC,故四边形ABCD是菱形.
15.解根据规则,画出符合要求的所有向量,马在B处走了“一步”的情况如图所示,
马在C处走了“一步”的情况如图所示.
16.ABD 由向量相等及共线的概念,结合图形可知C不一定正确.
17.解(1)画出所有的向量如图所示.
(2)由(1)所画的图知,
①当点C位于点C1或C2时,||取得最小值;
②当点C位于点C5或C6时,||取得最大值.
∴||的最大值为,最小值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
