数学:第十五章轴对称复习教案(冀教版八年级上)
文档属性
| 名称 | 数学:第十五章轴对称复习教案(冀教版八年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 48.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-13 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第十五章 轴对称
回顾与反思
〖教学目标〗
(-)知识目标
1.通过具体实例认识轴对称,理解它的基本性质;
2.能够按要求画出简单的平面图形经过一次(或二次)轴对称后的图形;
3.能利用轴对称进行图案设计,了解并欣赏物体的镜面对称;
4.了解等腰三角形的概念,掌握等腰三角形的性质和一个三角形是等腰三角形的条件;
5.了解等边三角形的概念及性质;利用等边三角形的性质探究一个锐角为角的直角三角形的边之间的关系.
(二)能力目标
体会解决问题的多样性,发展实践能力和创新能力.
(三)情感目标
认识丰富多彩的现实世界,形成初步的空间观念,逐步养成理解他人看法的意识,学会与他人交流.
〖教学重点〗
轴对称与等腰三角形.
〖教学难点〗
进行数学说理渗透.
〖教学过程〗
一、课前布置
阅读P71~P72回顾与反思,自己尝试着归纳本章的内容. 整理出本章的难点、重点,找出自己的疑点,盲点,出错点.
二、师生互动
[师]轴对称是一种生活中广泛存在的现象,通过本章的学习,你什么收获?
[生]我们了解了轴对称的基本性质,也体验了轴对称在生活中的广泛的应用,还欣赏了轴对称的美妙之处.
[生]在本章中,我们还研究了几何中最常见的最简单的轴对称图形,如:
角的轴对称性与角平分线的性质(角平分线上的点到这个角的两边的距离相等);
线段的轴对称性与线段的垂直平分线的性质(线段垂直平分线上的点到这条线段两个端点的距离相等);等腰三角形的轴对称性与等腰三角形的性质(等腰三角形顶角的平分线、底边上的中线、底边上的高重合,它们所在的直线是等腰三角形的对称轴)等等.
[生]我们还学习了等腰三角形的识别(等角对等边)和角的直角三角形的边之间的关系(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)
[师]这些简单的轴对称图形,通常是我们设计图案的基础.
[师生共研]常见的轴对称图形
图形 对称轴
点A 过A点的任意直线
直线l ①直线l ②l的垂线
线段AB ①直线AB ②线段AB的中垂线
角 角平分线所在的直线
等腰三角形 底边上的中线所在的直线
[生]我们还探索了轴对称的性质:
对应点所连的线段被对称轴垂直平分.
对应线段相等,对应角相等.
[师]我们还通过观察、折纸、简单图案设计等进一步了解了轴对称和轴对称图形.
(二)鼓励学生讲解教师提供的例题.(例题的设置是分层的,安排不同基础的学生尝试讲解,教师予以补充)
(本组例题是对冀教版课本内容的补充)
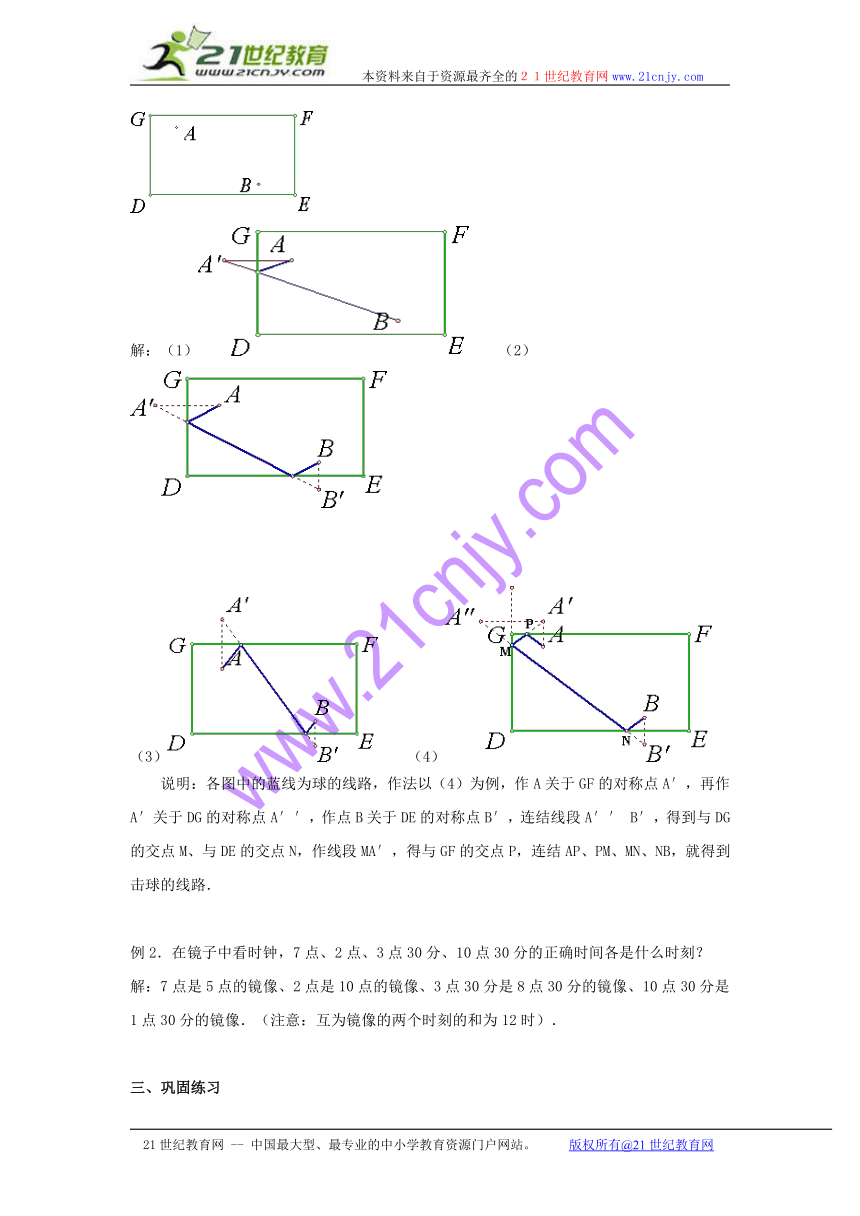
例1.如图,DEFG为矩形的台球桌面,现有球A、B位置如图,按下列要求,画出击打后球的线路.
(1)击打球A,使它碰撞台边DG后再击中球B;
(2)击打球A,使它碰撞台边DG,再碰撞台边DE后击中球B;
(3)击打球A,使它碰撞台边GF,再碰撞台边DE后击中球B;
(4)击打球A,使它碰撞台边GF,再碰撞台边DG,然后再碰撞台边DE后击中球B.
解:(1) (2)
(3) (4)
说明:各图中的蓝线为球的线路,作法以(4)为例,作A关于GF的对称点A′,再作A′关于DG的对称点A′′,作点B关于DE的对称点B′,连结线段A′′ B′,得到与DG的交点M、与DE的交点N,作线段MA′,得与GF的交点P,连结AP、PM、MN、NB,就得到击球的线路.
例2.在镜子中看时钟,7点、2点、3点30分、10点30分的正确时间各是什么时刻?
解:7点是5点的镜像、2点是10点的镜像、3点30分是8点30分的镜像、10点30分是1点30分的镜像.(注意:互为镜像的两个时刻的和为12时).
三、巩固练习
作业P72~76习题
1.选择题:
(1)等边三角形有( )条对称轴. A.1 B.2 C.3 D.6
(2)①直线 ②线段 ③平行四边形 ④梯形 ⑤角 ⑥等腰三角形;上述图形中,不是轴对称图形的有( )个. A.1 B.2 C.3 D.4
(3) 将一张正方形的纸片沿对角线对折后,得到一个等腰直角三角形,在这个重合的纸上剪出一个图案,打开后得到的图案至少有( )条对称轴. A.1 B.2 C.3 D.4
(4)如图是一个正五边形,AF是对称轴,则图中对应角相等的有( )对.
A.3 B.4 C.2 D.6
(5)A、B、C、D、E、F、G、H、I、J这十个字母中,
在镜子中看到的像与原字母相同的有( )个.
A.9 B.8 C.7 D.6
〖答案提示〗
1.(1)C (2)B (3)A (4)B (5)C
2.填空题:
(1)不在直线MN上的两个点A、B关于直线MN对称,则 垂直平分 .
(2)一个四边形是轴对称图形,有且只有四条对称轴,则这个四边形是 形.
(3)有一个内角为80°的等腰三角形,另外两个内角的度数分别是 .
(4)一位数字是轴对称的是 .
(5)有的汉字在镜子的两种放置下,它在镜子中的像都和原字相同,写出4个这样的汉字: .
〖答案提示〗
2. (1)直线MN, 线段AB; (2)正方形;
(3)50°、50°(顶角为80°时)或80°、20°(底角为80°时);
(4)1、3、8、0; (5)田、申、口、中、亘、王等.
3.以直线l为对称轴补全图形,看看象什么?
4.已知三个居民点A、B、C(如图),现要建一个服务中心P,使它到三个居民点A、B、C的距离相等,应建在何处?(画出点P的位置,简单说明理由)
5.画出下列轴对称图形的对称轴(有几条对称轴就画出几条,不要遗漏).
6.取一张正方形的纸片,沿对角线对折,得到一个等腰直角三角形,再沿这个三角形的对称轴对折,在得到的小三角形上剪出一个图案(发挥你的才能剪得漂亮些).打开后这个图形至少有几条对称轴?怎么做可以增加对称轴的条数?
〖答案提示〗
3.如图.
4.作线段AB、AC的垂直平分线,相交于点P,点P就是服务中心的位置.根据线段垂直平分线上的点到这条线段两个端点的距离相等。
5.如图,绿色的是对称轴(注意:右图的两条线本身所在直线也是对称轴).
6.得到的图形至少有两条对称轴.要想增加对称轴的条数,只要你在小三角形上剪的图形也是轴对称图形就可以了.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第十五章 轴对称
回顾与反思
〖教学目标〗
(-)知识目标
1.通过具体实例认识轴对称,理解它的基本性质;
2.能够按要求画出简单的平面图形经过一次(或二次)轴对称后的图形;
3.能利用轴对称进行图案设计,了解并欣赏物体的镜面对称;
4.了解等腰三角形的概念,掌握等腰三角形的性质和一个三角形是等腰三角形的条件;
5.了解等边三角形的概念及性质;利用等边三角形的性质探究一个锐角为角的直角三角形的边之间的关系.
(二)能力目标
体会解决问题的多样性,发展实践能力和创新能力.
(三)情感目标
认识丰富多彩的现实世界,形成初步的空间观念,逐步养成理解他人看法的意识,学会与他人交流.
〖教学重点〗
轴对称与等腰三角形.
〖教学难点〗
进行数学说理渗透.
〖教学过程〗
一、课前布置
阅读P71~P72回顾与反思,自己尝试着归纳本章的内容. 整理出本章的难点、重点,找出自己的疑点,盲点,出错点.
二、师生互动
[师]轴对称是一种生活中广泛存在的现象,通过本章的学习,你什么收获?
[生]我们了解了轴对称的基本性质,也体验了轴对称在生活中的广泛的应用,还欣赏了轴对称的美妙之处.
[生]在本章中,我们还研究了几何中最常见的最简单的轴对称图形,如:
角的轴对称性与角平分线的性质(角平分线上的点到这个角的两边的距离相等);
线段的轴对称性与线段的垂直平分线的性质(线段垂直平分线上的点到这条线段两个端点的距离相等);等腰三角形的轴对称性与等腰三角形的性质(等腰三角形顶角的平分线、底边上的中线、底边上的高重合,它们所在的直线是等腰三角形的对称轴)等等.
[生]我们还学习了等腰三角形的识别(等角对等边)和角的直角三角形的边之间的关系(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)
[师]这些简单的轴对称图形,通常是我们设计图案的基础.
[师生共研]常见的轴对称图形
图形 对称轴
点A 过A点的任意直线
直线l ①直线l ②l的垂线
线段AB ①直线AB ②线段AB的中垂线
角 角平分线所在的直线
等腰三角形 底边上的中线所在的直线
[生]我们还探索了轴对称的性质:
对应点所连的线段被对称轴垂直平分.
对应线段相等,对应角相等.
[师]我们还通过观察、折纸、简单图案设计等进一步了解了轴对称和轴对称图形.
(二)鼓励学生讲解教师提供的例题.(例题的设置是分层的,安排不同基础的学生尝试讲解,教师予以补充)
(本组例题是对冀教版课本内容的补充)
例1.如图,DEFG为矩形的台球桌面,现有球A、B位置如图,按下列要求,画出击打后球的线路.
(1)击打球A,使它碰撞台边DG后再击中球B;
(2)击打球A,使它碰撞台边DG,再碰撞台边DE后击中球B;
(3)击打球A,使它碰撞台边GF,再碰撞台边DE后击中球B;
(4)击打球A,使它碰撞台边GF,再碰撞台边DG,然后再碰撞台边DE后击中球B.
解:(1) (2)
(3) (4)
说明:各图中的蓝线为球的线路,作法以(4)为例,作A关于GF的对称点A′,再作A′关于DG的对称点A′′,作点B关于DE的对称点B′,连结线段A′′ B′,得到与DG的交点M、与DE的交点N,作线段MA′,得与GF的交点P,连结AP、PM、MN、NB,就得到击球的线路.
例2.在镜子中看时钟,7点、2点、3点30分、10点30分的正确时间各是什么时刻?
解:7点是5点的镜像、2点是10点的镜像、3点30分是8点30分的镜像、10点30分是1点30分的镜像.(注意:互为镜像的两个时刻的和为12时).
三、巩固练习
作业P72~76习题
1.选择题:
(1)等边三角形有( )条对称轴. A.1 B.2 C.3 D.6
(2)①直线 ②线段 ③平行四边形 ④梯形 ⑤角 ⑥等腰三角形;上述图形中,不是轴对称图形的有( )个. A.1 B.2 C.3 D.4
(3) 将一张正方形的纸片沿对角线对折后,得到一个等腰直角三角形,在这个重合的纸上剪出一个图案,打开后得到的图案至少有( )条对称轴. A.1 B.2 C.3 D.4
(4)如图是一个正五边形,AF是对称轴,则图中对应角相等的有( )对.
A.3 B.4 C.2 D.6
(5)A、B、C、D、E、F、G、H、I、J这十个字母中,
在镜子中看到的像与原字母相同的有( )个.
A.9 B.8 C.7 D.6
〖答案提示〗
1.(1)C (2)B (3)A (4)B (5)C
2.填空题:
(1)不在直线MN上的两个点A、B关于直线MN对称,则 垂直平分 .
(2)一个四边形是轴对称图形,有且只有四条对称轴,则这个四边形是 形.
(3)有一个内角为80°的等腰三角形,另外两个内角的度数分别是 .
(4)一位数字是轴对称的是 .
(5)有的汉字在镜子的两种放置下,它在镜子中的像都和原字相同,写出4个这样的汉字: .
〖答案提示〗
2. (1)直线MN, 线段AB; (2)正方形;
(3)50°、50°(顶角为80°时)或80°、20°(底角为80°时);
(4)1、3、8、0; (5)田、申、口、中、亘、王等.
3.以直线l为对称轴补全图形,看看象什么?
4.已知三个居民点A、B、C(如图),现要建一个服务中心P,使它到三个居民点A、B、C的距离相等,应建在何处?(画出点P的位置,简单说明理由)
5.画出下列轴对称图形的对称轴(有几条对称轴就画出几条,不要遗漏).
6.取一张正方形的纸片,沿对角线对折,得到一个等腰直角三角形,再沿这个三角形的对称轴对折,在得到的小三角形上剪出一个图案(发挥你的才能剪得漂亮些).打开后这个图形至少有几条对称轴?怎么做可以增加对称轴的条数?
〖答案提示〗
3.如图.
4.作线段AB、AC的垂直平分线,相交于点P,点P就是服务中心的位置.根据线段垂直平分线上的点到这条线段两个端点的距离相等。
5.如图,绿色的是对称轴(注意:右图的两条线本身所在直线也是对称轴).
6.得到的图形至少有两条对称轴.要想增加对称轴的条数,只要你在小三角形上剪的图形也是轴对称图形就可以了.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
