2024-2025学年人教A版数学必修第二册 第8章 立体几何初步 同步练习(含答案)
文档属性
| 名称 | 2024-2025学年人教A版数学必修第二册 第8章 立体几何初步 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 399.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 10:17:06 | ||
图片预览



文档简介
第8章 立体几何初步
一、选择题
1.在空间中,设m,n为两条不同的直线,α为一个平面,下列条件可判定m⊥n的是( )
A.m⊥α,n⊥α B.m∥α,n∥α
C.m⊥α,n∥α D.m∥α,且n α
2.已知m,n是空间中两条不同的直线,α,β是两个不同的平面,且m α,n β,则下列说法正确的是( )
A.若α∩β=l且α⊥β,m α,m⊥l,则m⊥β
B.若m∥n,则α∥β
C.若α∩β=l且m⊥l,n⊥l,则α⊥β
D.若α∥β,则m∥n
3.已知PA垂直于以AB为直径的圆所在的平面,C为圆上异于A,B两点的任一点,则下列关系不正确的是( )
A.PA⊥BC B.BC⊥平面PAC
C.AC⊥PB D.PC⊥BC
4.在空间四边形ABCD中,E,F分别是AB和BC上的点,若AE∶EB=CF∶FB=1∶2,则对角线AC和平面DEF的位置关系是( )
A.平行 B.相交
C.在平面内 D.不能确定
5.如图,在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,则下面四个结论不成立的是( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面PAE
D.平面PDE⊥平面ABC
6.(多选题)(2023·山东青岛期末)如图,在梯形ABCD中,AD∥BC,AD=AB =1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A 的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题,其中正确的是( )
A.A′D⊥BC
B.三棱锥A′-BCD的体积为
C.BA′⊥CA′
D.平面A′BC⊥平面A′DC
7.在长方体ABCD-A1B1C1D1中,AA1=AD=2AB.若E,F分别为线段A1D1,CC1的中点,则直线EF与平面ADD1A1所成角的正弦值为( )
A. B.
C. D.
8.(多选题)如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下面四个命题:
①没有水的部分始终呈棱柱形;
②水面EFGH所在四边形的面积为定值;
③棱A1D1始终与水面所在平面平行;
④当容器倾斜如图所示时,BE·BF是定值.
其中正确的命题是( )
A.① B.②
C.③ D.④
二、填空题
9.已知直线l,a,b,平面α,若要得到结论l⊥α,则需要在条件a α,b α,l⊥a,l⊥b中另外添加的一个条件是___.
10.如图,已知∠BAC=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中,与PC垂直的直线有___条;与AP垂直的直线有___条.
11.已知三条不同的直线a,b,c和两个不同的平面α,β满足以下条件:①a⊥α,b⊥β;②α∩β=m;③c⊥a,c⊥b,c α,c β,则c与m的位置关系是___.(填“相交”,“平行”或“异面”)
12.已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为___.
13.如图所示,等边三角形ABC的边长为4,D为BC的中点,沿AD把△ADC折叠到△ADC′处,使二面角B-AD-C′为60°,则折叠后二面角A-BC′-D的正切值为___.
三、解答题
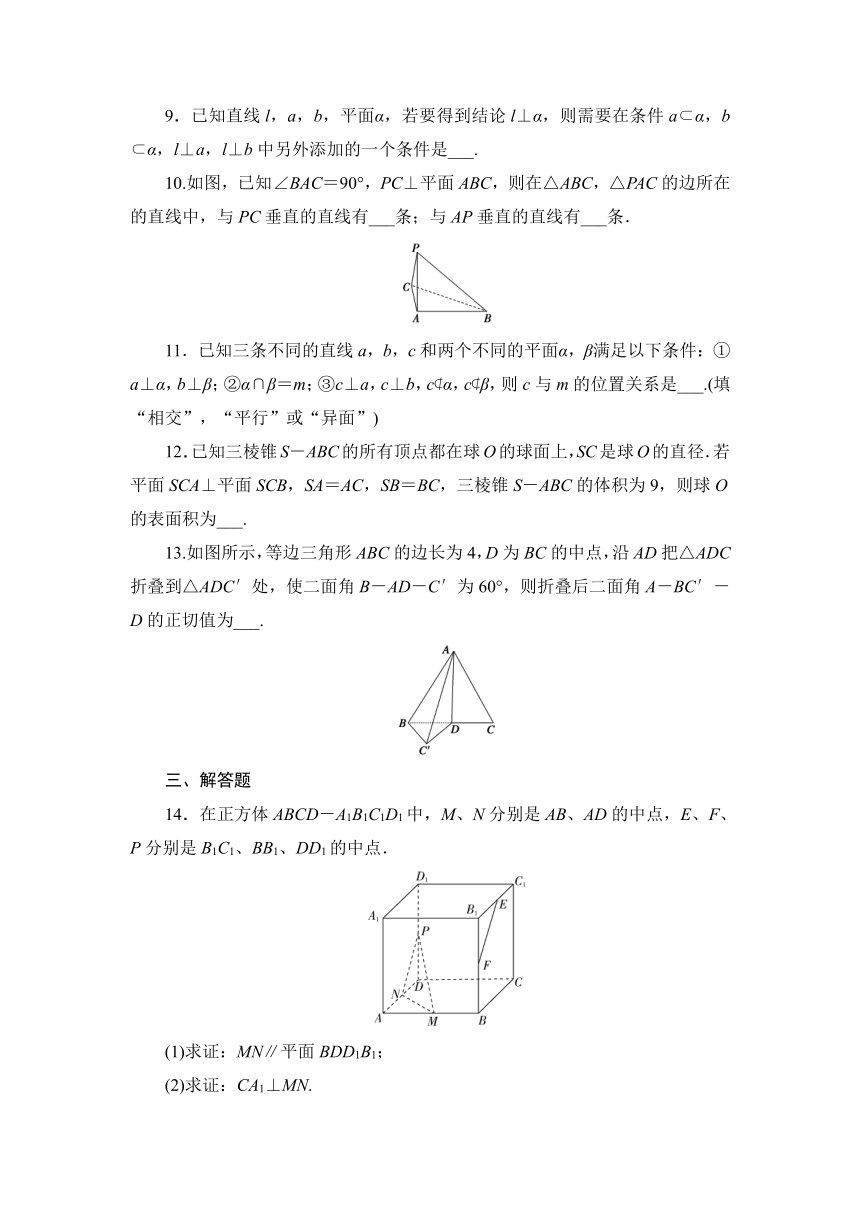
14.在正方体ABCD-A1B1C1D1中,M、N分别是AB、AD的中点,E、F、P分别是B1C1、BB1、DD1的中点.
(1)求证:MN∥平面BDD1B1;
(2)求证:CA1⊥MN.
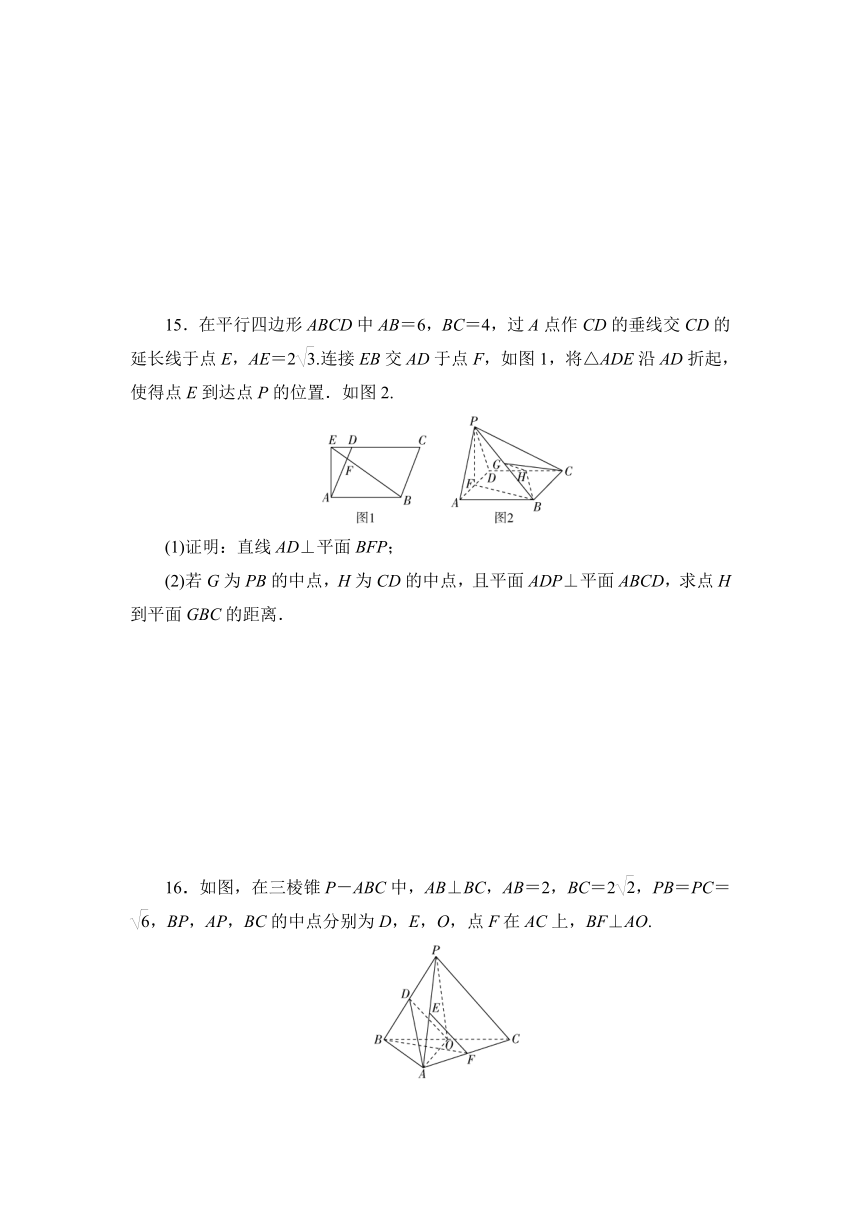
15.在平行四边形ABCD中AB=6,BC=4,过A点作CD的垂线交CD的延长线于点E,AE=2.连接EB交AD于点F,如图1,将△ADE沿AD折起,使得点E到达点P的位置.如图2.
(1)证明:直线AD⊥平面BFP;
(2)若G为PB的中点,H为CD的中点,且平面ADP⊥平面ABCD,求点H到平面GBC的距离.
16.如图,在三棱锥P-ABC中,AB⊥BC,AB=2,BC=2,PB=PC=,BP,AP,BC的中点分别为D,E,O,点F在AC上,BF⊥AO.
(1)求证:EF∥平面ADO;
(2)若∠POF=120°,求三棱锥P-ABC的体积.
17. 如图所示,四棱柱ABCD-A1B1C1D1的底面是菱形,侧棱垂直于底面,点E,F分别在棱AA1,CC1上,且满足AE=AA1,CF=CC1,平面BEF与平面ABC的交线为l.
(1)证明:直线l⊥平面BDD1;
(2)已知EF=2,BD1=4,设BF与平面BDD1所成的角为θ,求sin θ的取值范围.
第8章 立体几何初步
一、选择题
1.C
当m⊥α,n⊥α时,m∥n,所以A选项错误;当m∥α,n∥α时,m,n可能平行,所以B选项错误;当m⊥α,n∥α时,m⊥n,所以C选项正确;当m∥α,且n α时,m,n可能平行,所以D选项错误.故选C.
2. A
若α∩β=l且α⊥β,m α,m⊥l,则m⊥β,由面面垂直性质定理得出A正确;若m∥n,且m α,n β,则α∥β或α与β相交,故B错误;若m α,n β,α∩β=l,且m⊥l,n⊥l,则α与β相交,可能垂直,也可能不垂直,故C错误;两个平面平行,不能证明两个平面里的直线都平行,可能异面, 故D错误;故选A.
3.C
由PA⊥平面ACB PA⊥BC,故A不符合题意;由BC⊥PA,BC⊥AC,PA∩AC=A,可得BC⊥平面PAC,所以BC⊥PC,故B、D不符合题意;AC⊥PB显然不成立,故C符合题意.
4. A
如图,由=得AC∥EF.又因为EF 平面DEF,AC 平面DEF,所以AC∥平面DEF.
5. D
因为BC∥DF,DF 平面PDF,BC 平面PDF,所以BC∥平面PDF,故选项A正确;在正四面体P-ABC中,AE⊥BC,PE⊥BC,AE∩PE=E,所以BC⊥平面PAE,又DF∥BC,则DF⊥平面PAE,从而平面PDF⊥平面PAE.因此选项B、C均正确.
6.C D
如图所示,E为BD的中点,连接A′E.因为A′D=A′B,
所以A′E⊥BD,因为平面A′BD⊥平面BCD,
平面A′BD∩平面BCD=BD,A′E 平面A′BD,
所以A′E⊥平面BCD,所以A′E⊥BC.
若A′D⊥BC,则可得到BC⊥平面A′BD,故BC⊥BD,与已知矛盾,故A错误.
易得三棱锥A′-BCD的体积V=××××=,故B错误.
易知△A′CD为直角三角形,则A′C=.在△A′BC中,A′B=1,BC=2,A′C=,满足BC2=A′B2+A′C2,所以BA′⊥CA′.故C正确.
因为BA′⊥DA′,DA′∩CA′=A′,所以BA′⊥平面A′DC,因为BA′ 平面A′BC,所以平面A′BC⊥平面A′DC,故D正确.故选CD.
7.C
取DD1的中点G,连接EG、FG、EC1,易知∠FEG为直线EF与平面ADD1A1所成的角,设AB=a,则AA1=AD=2a,在△ED1C1中可求出EC1=a,在△EFC1中可求出EF=a,所以在△EFG中,sin∠FEG==,故选C.
8.ACD
由题图,显然①是正确的,②是错误的;对于③,∵A1D1∥BC,BC∥FG,
∴A1D1∥FG且A1D1 平面EFGH,FG 平面EFGH,
∴A1D1∥平面EFGH(水面).∴③是正确的;
对于④,∵水是定量的(定体积V),
∴S△BEF·BC=V,即BE·BF·BC=V.
∴BE·BF=(定值),即④是正确的,故选ACD.
二、填空题
9. _a与b相交__.
由线面垂直的判定定理得到,a与b相交.
故答案为a与b相交.
10. 3__; _1__.
∵PC⊥平面ABC,
∴PC垂直于直线AB,BC,AC.
∵AB⊥AC,AB⊥PC,AC∩PC=C,∴AB⊥平面PAC,
又∵AP 平面PAC,
∴AB⊥AP,与AP垂直的直线是AB.
11. _平行__.
由题意可知,直线a与直线b不平行,过a上一点A作直线b′∥b,如图所示,
则a与b′确定一个平面γ,
由a⊥α,a γ,则γ⊥α,
由b⊥β,b′∥b,则b′⊥β,又b′ γ,则γ⊥β,
由α∩β=m,得m⊥γ,
由c⊥b,得c⊥b′,又c⊥a,a∩b′=A,a,b′ γ,所以c⊥γ,
c α,c β,所以c∥m.
故答案为平行.
12. _36π__.
设球O的半径为R,∵SC为球O的直径,∴点O为SC的中点.连接AO,OB,∵SA=AC,SB=BC,∴AO⊥SC,∴BO⊥SC.∵平面SCA⊥平面SCB,平面SCA∩平面SCB=SC,AO 平面SCA,∴AO⊥平面SCB,所以VS-ABC=VA-SBC=×S△SBC×AO=××AO,即9=××R,解得R=3,∴球O的表面积为S=4πR2=4π×32=36π.
13. _2__.
易知∠BDC′即二面角B-AD-C′的平面角,有∠BDC′=60°,所以△BDC′为等边三角形.取BC′的中点M,连接DM,AM,则易知DM⊥BC′,AM⊥BC′,所以二面角A-BC′-D的平面角即∠AMD.在等边三角形ABC中,易知AD=2,在等边三角形BDC′中,易知DM=,所以tan∠AMD==2.
三、解答题
14. (1)连接BD,B1D1,∵MN∥BD,MN 面BDD1B1,BD 平面BDD1B1,
∴MN∥平面BDD1B1.
(2)AA1⊥平面ABCD,MN 平面ABCD,∴AA1⊥MN,
∵AC⊥BD,MN∥BD,∴AC⊥MN.
又∵AA1∩AC=A,∴MN⊥平面A1AC,∴CA1⊥MN.
15. (1)证明:图1中,在Rt△BAE中,AB=6,AE=2,所以∠AEB=60°.所以BE=4.
∵△ADE也是直角三角形,∴DE==2,
∴==,
∵∠AED=∠EAB=90°,
∴△AEB∽△EDA,∴∠EAD=∠ABE,
∴∠DAB+∠ABE=∠DAB+∠EAD=90°,∴BE⊥AD,
在图2中,PF⊥AD,BF⊥AD,PF∩BF=F,所以AD⊥平面BFP.
(2)∵平面ADP⊥平面ABCD,且平面ADP∩平面ABCD=AD,
PF 平面ADP,PF⊥AD,∴PF⊥平面ABCD.
取BF的中点为O,连接GO,则GO∥PF,
∴GO⊥平面ABCD,即GO为三棱锥G-BCH的高.
∴GO=PF=×PAsin30°=.
∵CH=DC=3,∴S△BCH=CH·AE=×3×2=3,
∴VG-BCH=S△BCH·GO=×3×=.
又∵BC⊥BF,PF⊥BC,又BF∩PF=F,
∴BC⊥平面PBF,∴BC⊥BG,
GB=PB==,
∴S△GBC=××4=.
设点H到平面GBC的距离为d,则由VH-GBC=VG-BCH,
得·d=,解得d=.
∴点H到平面GBC的距离为.
16. (1)证明:连接DE,OF,设AF=tAC,则=+=(1-t)+t,=-+.又因为BF⊥AO,所以·=[(1-t)+t]·=(t-1)2+t=4(t-1)+4t=0,
解得t=,则F为AC的中点.
由D,E,O,F分别为PB,PA,BC,AC的中点,
于是DE∥AB,DE=AB,OF∥AB,OF=AB,即DE∥OF,DE=OF,
则四边形ODEF为平行四边形,
所以EF∥DO,又EF 平面ADO,DO 平面ADO,
所以EF∥平面ADO.
(2)过P作PM垂直FO的延长线交于点M,
因为PB=PC,O是BC中点,所以PO⊥BC,
在Rt△PBO中,PB=,BO=BC=,
所以PO===2,
因为AB⊥BC,OF∥AB,
所以OF⊥BC,又PO∩OF=O,PO,OF 平面POF,
所以BC⊥平面POF,又PM 平面POF,
所以BC⊥PM,又BC∩FM=O,BC,FM 平面ABC,
所以PM⊥平面ABC,
即三棱锥P-ABC的高为PM,
因为∠POF=120°,所以∠POM=60°,
所以PM=POsin 60°=2×=,
又S△ABC=AB·BC=×2×2=2,
所以VP-ABC=S△ABC·PM=×2×=.
17. (1)证明:如图,连接AC,与BD交于点O.
由条件可知AE∥CF,且AE=CF,所以AC∥EF,
因为EF 平面BEF,AC 平面BEF,所以AC∥平面BEF.
因为平面BEF∩平面ABC=l,所以AC∥l.
因为四棱柱ABCD-A1B1C1D1的底面是菱形,且侧棱垂直于底面,
所以AC⊥BD,AC⊥BB1,
又BD∩BB1=B,所以AC⊥平面BDD1,
所以l⊥平面BDD1.
(2)设EF∩平面BDD1=H,连接BH.
由(1)知EH⊥平面BDD1,故∠HBF=θ.
则sin θ==.
令BO=a,则BD=2a在Rt△D1DB中,DD1==2,
∴FC=HO=,
∴在Rt△HOB中HB==,
∴在Rt△FHB中,BF==,
∴sin θ=,
由0
一、选择题
1.在空间中,设m,n为两条不同的直线,α为一个平面,下列条件可判定m⊥n的是( )
A.m⊥α,n⊥α B.m∥α,n∥α
C.m⊥α,n∥α D.m∥α,且n α
2.已知m,n是空间中两条不同的直线,α,β是两个不同的平面,且m α,n β,则下列说法正确的是( )
A.若α∩β=l且α⊥β,m α,m⊥l,则m⊥β
B.若m∥n,则α∥β
C.若α∩β=l且m⊥l,n⊥l,则α⊥β
D.若α∥β,则m∥n
3.已知PA垂直于以AB为直径的圆所在的平面,C为圆上异于A,B两点的任一点,则下列关系不正确的是( )
A.PA⊥BC B.BC⊥平面PAC
C.AC⊥PB D.PC⊥BC
4.在空间四边形ABCD中,E,F分别是AB和BC上的点,若AE∶EB=CF∶FB=1∶2,则对角线AC和平面DEF的位置关系是( )
A.平行 B.相交
C.在平面内 D.不能确定
5.如图,在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,则下面四个结论不成立的是( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面PAE
D.平面PDE⊥平面ABC
6.(多选题)(2023·山东青岛期末)如图,在梯形ABCD中,AD∥BC,AD=AB =1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起.设折起后点A 的位置为A′,并且平面A′BD⊥平面BCD.给出下面四个命题,其中正确的是( )
A.A′D⊥BC
B.三棱锥A′-BCD的体积为
C.BA′⊥CA′
D.平面A′BC⊥平面A′DC
7.在长方体ABCD-A1B1C1D1中,AA1=AD=2AB.若E,F分别为线段A1D1,CC1的中点,则直线EF与平面ADD1A1所成角的正弦值为( )
A. B.
C. D.
8.(多选题)如图,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜度的不同,有下面四个命题:
①没有水的部分始终呈棱柱形;
②水面EFGH所在四边形的面积为定值;
③棱A1D1始终与水面所在平面平行;
④当容器倾斜如图所示时,BE·BF是定值.
其中正确的命题是( )
A.① B.②
C.③ D.④
二、填空题
9.已知直线l,a,b,平面α,若要得到结论l⊥α,则需要在条件a α,b α,l⊥a,l⊥b中另外添加的一个条件是___.
10.如图,已知∠BAC=90°,PC⊥平面ABC,则在△ABC,△PAC的边所在的直线中,与PC垂直的直线有___条;与AP垂直的直线有___条.
11.已知三条不同的直线a,b,c和两个不同的平面α,β满足以下条件:①a⊥α,b⊥β;②α∩β=m;③c⊥a,c⊥b,c α,c β,则c与m的位置关系是___.(填“相交”,“平行”或“异面”)
12.已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为___.
13.如图所示,等边三角形ABC的边长为4,D为BC的中点,沿AD把△ADC折叠到△ADC′处,使二面角B-AD-C′为60°,则折叠后二面角A-BC′-D的正切值为___.
三、解答题
14.在正方体ABCD-A1B1C1D1中,M、N分别是AB、AD的中点,E、F、P分别是B1C1、BB1、DD1的中点.
(1)求证:MN∥平面BDD1B1;
(2)求证:CA1⊥MN.
15.在平行四边形ABCD中AB=6,BC=4,过A点作CD的垂线交CD的延长线于点E,AE=2.连接EB交AD于点F,如图1,将△ADE沿AD折起,使得点E到达点P的位置.如图2.
(1)证明:直线AD⊥平面BFP;
(2)若G为PB的中点,H为CD的中点,且平面ADP⊥平面ABCD,求点H到平面GBC的距离.
16.如图,在三棱锥P-ABC中,AB⊥BC,AB=2,BC=2,PB=PC=,BP,AP,BC的中点分别为D,E,O,点F在AC上,BF⊥AO.
(1)求证:EF∥平面ADO;
(2)若∠POF=120°,求三棱锥P-ABC的体积.
17. 如图所示,四棱柱ABCD-A1B1C1D1的底面是菱形,侧棱垂直于底面,点E,F分别在棱AA1,CC1上,且满足AE=AA1,CF=CC1,平面BEF与平面ABC的交线为l.
(1)证明:直线l⊥平面BDD1;
(2)已知EF=2,BD1=4,设BF与平面BDD1所成的角为θ,求sin θ的取值范围.
第8章 立体几何初步
一、选择题
1.C
当m⊥α,n⊥α时,m∥n,所以A选项错误;当m∥α,n∥α时,m,n可能平行,所以B选项错误;当m⊥α,n∥α时,m⊥n,所以C选项正确;当m∥α,且n α时,m,n可能平行,所以D选项错误.故选C.
2. A
若α∩β=l且α⊥β,m α,m⊥l,则m⊥β,由面面垂直性质定理得出A正确;若m∥n,且m α,n β,则α∥β或α与β相交,故B错误;若m α,n β,α∩β=l,且m⊥l,n⊥l,则α与β相交,可能垂直,也可能不垂直,故C错误;两个平面平行,不能证明两个平面里的直线都平行,可能异面, 故D错误;故选A.
3.C
由PA⊥平面ACB PA⊥BC,故A不符合题意;由BC⊥PA,BC⊥AC,PA∩AC=A,可得BC⊥平面PAC,所以BC⊥PC,故B、D不符合题意;AC⊥PB显然不成立,故C符合题意.
4. A
如图,由=得AC∥EF.又因为EF 平面DEF,AC 平面DEF,所以AC∥平面DEF.
5. D
因为BC∥DF,DF 平面PDF,BC 平面PDF,所以BC∥平面PDF,故选项A正确;在正四面体P-ABC中,AE⊥BC,PE⊥BC,AE∩PE=E,所以BC⊥平面PAE,又DF∥BC,则DF⊥平面PAE,从而平面PDF⊥平面PAE.因此选项B、C均正确.
6.C D
如图所示,E为BD的中点,连接A′E.因为A′D=A′B,
所以A′E⊥BD,因为平面A′BD⊥平面BCD,
平面A′BD∩平面BCD=BD,A′E 平面A′BD,
所以A′E⊥平面BCD,所以A′E⊥BC.
若A′D⊥BC,则可得到BC⊥平面A′BD,故BC⊥BD,与已知矛盾,故A错误.
易得三棱锥A′-BCD的体积V=××××=,故B错误.
易知△A′CD为直角三角形,则A′C=.在△A′BC中,A′B=1,BC=2,A′C=,满足BC2=A′B2+A′C2,所以BA′⊥CA′.故C正确.
因为BA′⊥DA′,DA′∩CA′=A′,所以BA′⊥平面A′DC,因为BA′ 平面A′BC,所以平面A′BC⊥平面A′DC,故D正确.故选CD.
7.C
取DD1的中点G,连接EG、FG、EC1,易知∠FEG为直线EF与平面ADD1A1所成的角,设AB=a,则AA1=AD=2a,在△ED1C1中可求出EC1=a,在△EFC1中可求出EF=a,所以在△EFG中,sin∠FEG==,故选C.
8.ACD
由题图,显然①是正确的,②是错误的;对于③,∵A1D1∥BC,BC∥FG,
∴A1D1∥FG且A1D1 平面EFGH,FG 平面EFGH,
∴A1D1∥平面EFGH(水面).∴③是正确的;
对于④,∵水是定量的(定体积V),
∴S△BEF·BC=V,即BE·BF·BC=V.
∴BE·BF=(定值),即④是正确的,故选ACD.
二、填空题
9. _a与b相交__.
由线面垂直的判定定理得到,a与b相交.
故答案为a与b相交.
10. 3__; _1__.
∵PC⊥平面ABC,
∴PC垂直于直线AB,BC,AC.
∵AB⊥AC,AB⊥PC,AC∩PC=C,∴AB⊥平面PAC,
又∵AP 平面PAC,
∴AB⊥AP,与AP垂直的直线是AB.
11. _平行__.
由题意可知,直线a与直线b不平行,过a上一点A作直线b′∥b,如图所示,
则a与b′确定一个平面γ,
由a⊥α,a γ,则γ⊥α,
由b⊥β,b′∥b,则b′⊥β,又b′ γ,则γ⊥β,
由α∩β=m,得m⊥γ,
由c⊥b,得c⊥b′,又c⊥a,a∩b′=A,a,b′ γ,所以c⊥γ,
c α,c β,所以c∥m.
故答案为平行.
12. _36π__.
设球O的半径为R,∵SC为球O的直径,∴点O为SC的中点.连接AO,OB,∵SA=AC,SB=BC,∴AO⊥SC,∴BO⊥SC.∵平面SCA⊥平面SCB,平面SCA∩平面SCB=SC,AO 平面SCA,∴AO⊥平面SCB,所以VS-ABC=VA-SBC=×S△SBC×AO=××AO,即9=××R,解得R=3,∴球O的表面积为S=4πR2=4π×32=36π.
13. _2__.
易知∠BDC′即二面角B-AD-C′的平面角,有∠BDC′=60°,所以△BDC′为等边三角形.取BC′的中点M,连接DM,AM,则易知DM⊥BC′,AM⊥BC′,所以二面角A-BC′-D的平面角即∠AMD.在等边三角形ABC中,易知AD=2,在等边三角形BDC′中,易知DM=,所以tan∠AMD==2.
三、解答题
14. (1)连接BD,B1D1,∵MN∥BD,MN 面BDD1B1,BD 平面BDD1B1,
∴MN∥平面BDD1B1.
(2)AA1⊥平面ABCD,MN 平面ABCD,∴AA1⊥MN,
∵AC⊥BD,MN∥BD,∴AC⊥MN.
又∵AA1∩AC=A,∴MN⊥平面A1AC,∴CA1⊥MN.
15. (1)证明:图1中,在Rt△BAE中,AB=6,AE=2,所以∠AEB=60°.所以BE=4.
∵△ADE也是直角三角形,∴DE==2,
∴==,
∵∠AED=∠EAB=90°,
∴△AEB∽△EDA,∴∠EAD=∠ABE,
∴∠DAB+∠ABE=∠DAB+∠EAD=90°,∴BE⊥AD,
在图2中,PF⊥AD,BF⊥AD,PF∩BF=F,所以AD⊥平面BFP.
(2)∵平面ADP⊥平面ABCD,且平面ADP∩平面ABCD=AD,
PF 平面ADP,PF⊥AD,∴PF⊥平面ABCD.
取BF的中点为O,连接GO,则GO∥PF,
∴GO⊥平面ABCD,即GO为三棱锥G-BCH的高.
∴GO=PF=×PAsin30°=.
∵CH=DC=3,∴S△BCH=CH·AE=×3×2=3,
∴VG-BCH=S△BCH·GO=×3×=.
又∵BC⊥BF,PF⊥BC,又BF∩PF=F,
∴BC⊥平面PBF,∴BC⊥BG,
GB=PB==,
∴S△GBC=××4=.
设点H到平面GBC的距离为d,则由VH-GBC=VG-BCH,
得·d=,解得d=.
∴点H到平面GBC的距离为.
16. (1)证明:连接DE,OF,设AF=tAC,则=+=(1-t)+t,=-+.又因为BF⊥AO,所以·=[(1-t)+t]·=(t-1)2+t=4(t-1)+4t=0,
解得t=,则F为AC的中点.
由D,E,O,F分别为PB,PA,BC,AC的中点,
于是DE∥AB,DE=AB,OF∥AB,OF=AB,即DE∥OF,DE=OF,
则四边形ODEF为平行四边形,
所以EF∥DO,又EF 平面ADO,DO 平面ADO,
所以EF∥平面ADO.
(2)过P作PM垂直FO的延长线交于点M,
因为PB=PC,O是BC中点,所以PO⊥BC,
在Rt△PBO中,PB=,BO=BC=,
所以PO===2,
因为AB⊥BC,OF∥AB,
所以OF⊥BC,又PO∩OF=O,PO,OF 平面POF,
所以BC⊥平面POF,又PM 平面POF,
所以BC⊥PM,又BC∩FM=O,BC,FM 平面ABC,
所以PM⊥平面ABC,
即三棱锥P-ABC的高为PM,
因为∠POF=120°,所以∠POM=60°,
所以PM=POsin 60°=2×=,
又S△ABC=AB·BC=×2×2=2,
所以VP-ABC=S△ABC·PM=×2×=.
17. (1)证明:如图,连接AC,与BD交于点O.
由条件可知AE∥CF,且AE=CF,所以AC∥EF,
因为EF 平面BEF,AC 平面BEF,所以AC∥平面BEF.
因为平面BEF∩平面ABC=l,所以AC∥l.
因为四棱柱ABCD-A1B1C1D1的底面是菱形,且侧棱垂直于底面,
所以AC⊥BD,AC⊥BB1,
又BD∩BB1=B,所以AC⊥平面BDD1,
所以l⊥平面BDD1.
(2)设EF∩平面BDD1=H,连接BH.
由(1)知EH⊥平面BDD1,故∠HBF=θ.
则sin θ==.
令BO=a,则BD=2a
∴FC=HO=,
∴在Rt△HOB中HB==,
∴在Rt△FHB中,BF==,
∴sin θ=,
由0
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
