华师大版七下(2024版)9.4中心对称学案
文档属性
| 名称 | 华师大版七下(2024版)9.4中心对称学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 945.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第9章轴对称、平移与旋转
9.4 中心对称
学习目标与重难点
学习目标:
1.能说出中心对称的定义并指出对称中心;能运用中心对称性质作出简单图形的对称点;
2. 通过 “观察特例→归纳定义→验证性质→规范作图” 的探究过程,发展几何直观与逻辑推理能力,体会从特殊到一般的数学思维。
3. 发现中心对称在艺术设计、建筑结构中的对称美,体会数学对现实世界的规律提炼作用,增强 “用数学眼光欣赏生活” 的意识。
学习重点: 1. 中心对称的概念理解:明确 “中心对称图形” 与 “两图形成中心对称” 的区别与联系;掌握对称中心的核心作用 —— 所有对称点连线的中点。
2. 中心对称的作图方法:熟练运用 “延长法” 作出对称点.
学习难点:中心对称性质的综合应用,在复杂情境中,能逆向运用 “对称点连线被对称中心平分” 的性质解决问题。
预习自测
知识链接
1.中心对称图形是旋转对称图形吗?
2.在线段、直角、正方形、长方形、正五边形中,是中心对称图形的有哪些?
3.如何确定对称中心?
自学自测
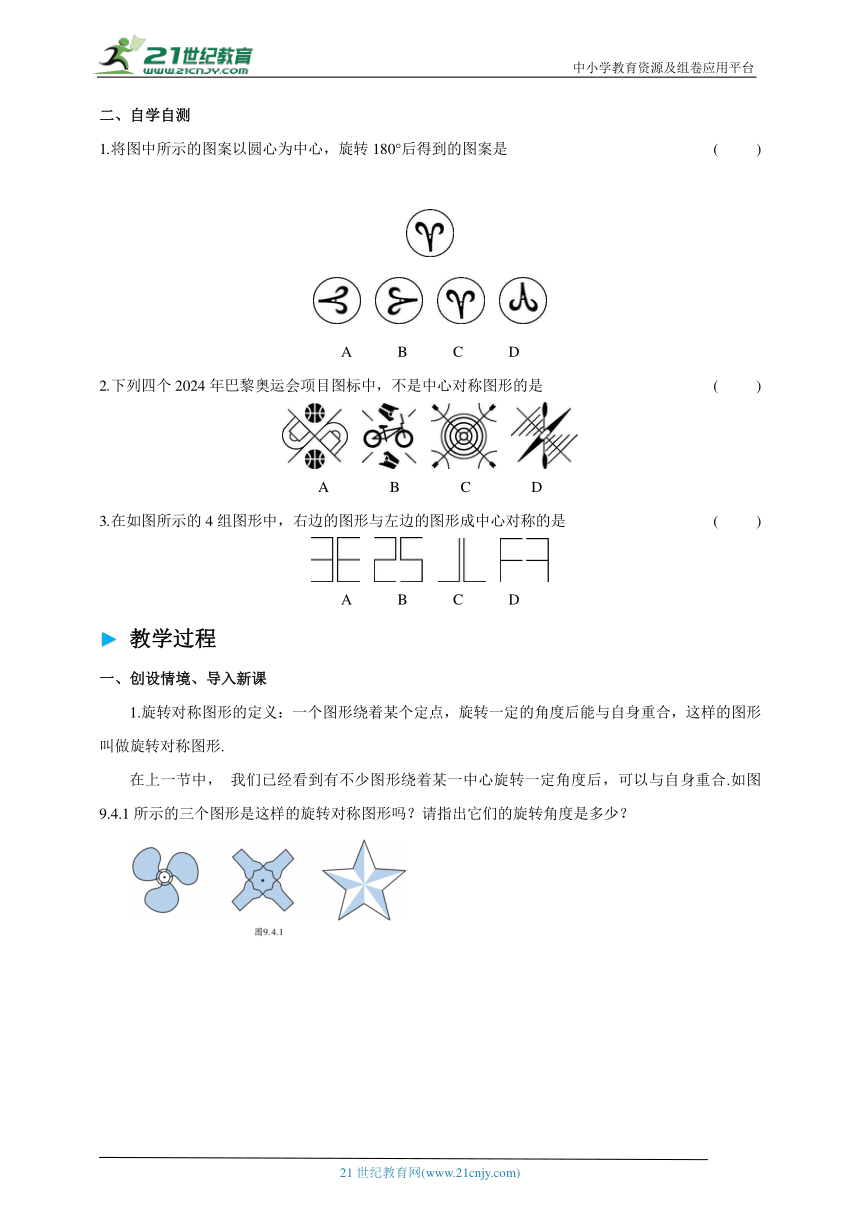
1.将图中所示的图案以圆心为中心,旋转180°后得到的图案是 ( )
A B C D
2.下列四个2024年巴黎奥运会项目图标中,不是中心对称图形的是 ( )
A B C D
3.在如图所示的4组图形中,右边的图形与左边的图形成中心对称的是 ( )
A B C D
教学过程
一、创设情境、导入新课
1.旋转对称图形的定义:一个图形绕着某个定点,旋转一定的角度后能与自身重合,这样的图形叫做旋转对称图形.
在上一节中, 我们已经看到有不少图形绕着某一中心旋转一定角度后,可以与自身重合.如图9.4.1所示的三个图形是这样的旋转对称图形吗?请指出它们的旋转角度是多少?
二、合作交流、新知探究
探究一: 中心对称图形的认识
教材第149页:
问题1:将下面的图形绕O点旋转180°,你有什么发现?
提取概念:
中心对称图形:
_______________________________________________________________________________________
_______________________________________________________________________________________
对称中心:
_______________________________________________________________________________________
中心对称图形是旋转角度为180°的旋转对称图形,你能举出一些这样的实例吗?
问题2:观察下列图形的运动,说一说它们有什么共同点.
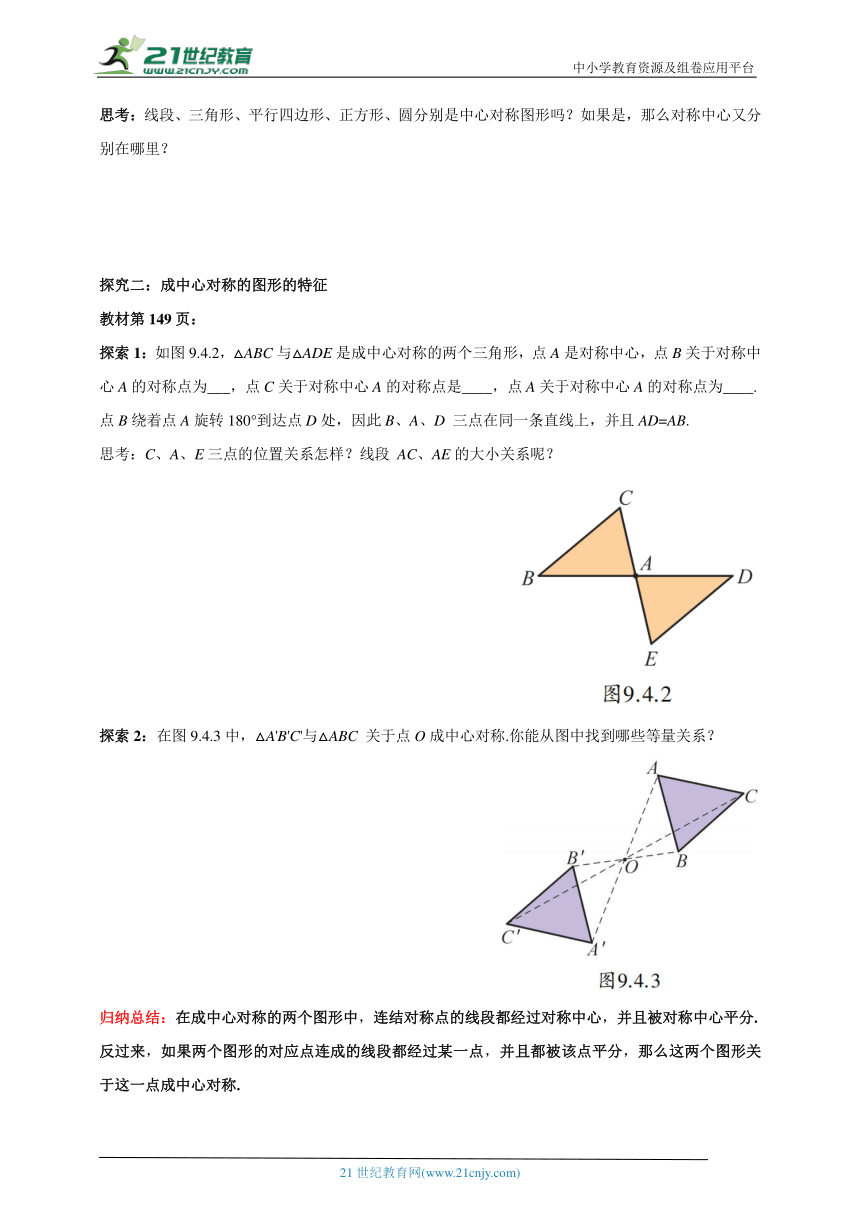
思考:线段、三角形、平行四边形、正方形、圆分别是中心对称图形吗?如果是,那么对称中心又分别在哪里?
探究二:成中心对称的图形的特征
教材第149页:
探索1:如图9.4.2,△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,点B关于对称中心A的对称点为___,点C关于对称中心A的对称点是____,点A关于对称中心A的对称点为____.
点B绕着点A旋转180°到达点D处,因此B、A、D 三点在同一条直线上,并且AD=AB.
思考:C、A、E三点的位置关系怎样?线段 AC、AE的大小关系呢?
探索2:在图9.4.3中,△A'B'C'与△ABC 关于点O成中心对称.你能从图中找到哪些等量关系?
归纳总结:在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
探究三:例题讲解
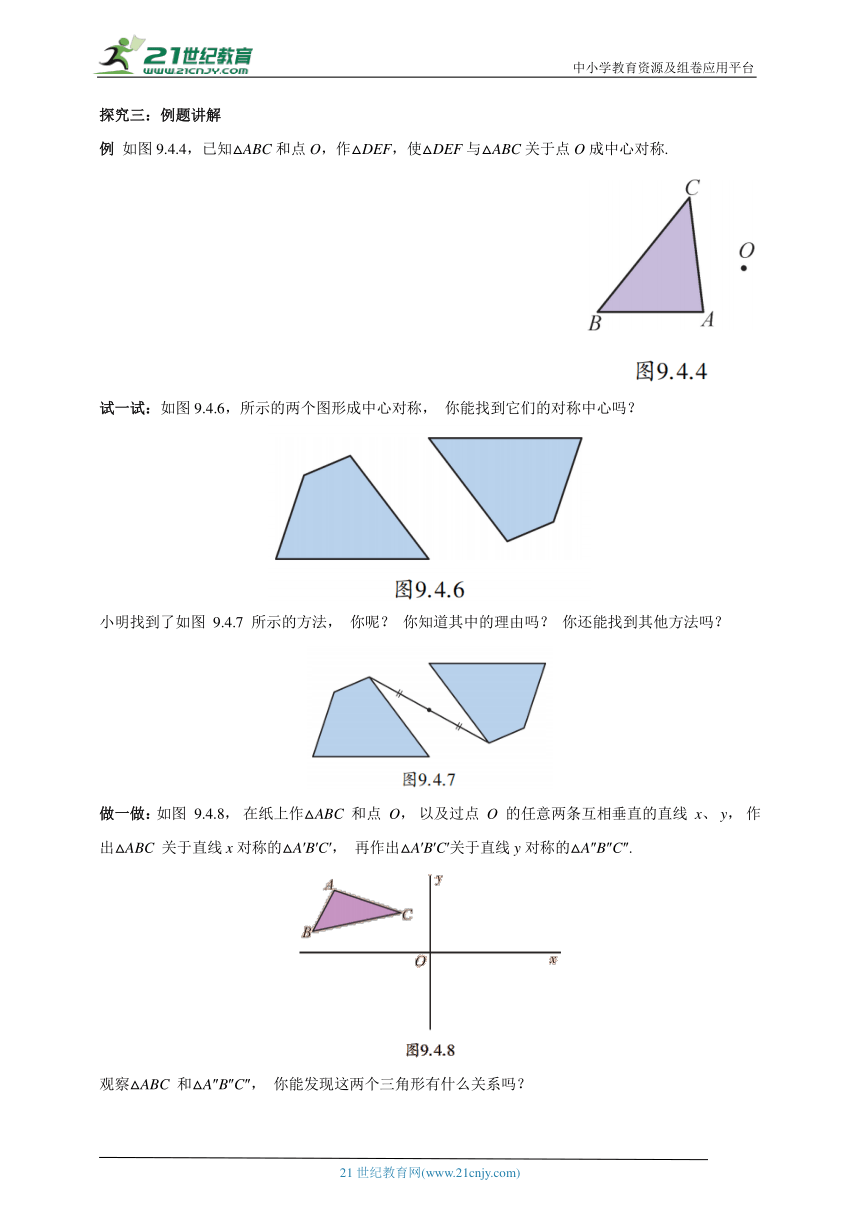
例 如图9.4.4,已知△ABC和点O,作△DEF,使△DEF与△ABC关于点O成中心对称.
试一试:如图9.4.6,所示的两个图形成中心对称, 你能找到它们的对称中心吗?
小明找到了如图 9.4.7 所示的方法, 你呢? 你知道其中的理由吗? 你还能找到其他方法吗?
做一做:如图 9.4.8, 在纸上作△ABC 和点 O, 以及过点 O 的任意两条互相垂直的直线 x、 y, 作出△ABC 关于直线x对称的△A′B′C′, 再作出△A′B′C′关于直线y对称的△A″B″C″.
观察△ABC 和△A″B″C″, 你能发现这两个三角形有什么关系吗?
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.剪纸是中国传统的民间艺术,下列各剪纸图案中,不是中心对称图形的是( )
2.下列命题中:
①中心对称图形一定是轴对称图形;②有两条互相垂直的对称轴的轴对称图形一定是中心对称图形;③关于某一点为中心对称的两个三角形能重合;④两个重合的图形一定为中心对称.其中正确的个数为( )
A.1 B.2 C.3 D.4
3.已知每组中的两个图形分别关于某点成中心对称,画出对称中心.
选做题:
4.下列各组图形中,△A'B'C'与△ABC成中心对称的是( )
5.已知六边形ABCDEF是以O为中心的中心对称图形(如图),画出六边形ABCDEF的全部图形,并指出所有的对应点和对应线段.
6.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
【综合拓展类作业】
7.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成中心对称且也以格点为顶点的三角形共有 ;(不包括△ABC本身)
8.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,四边形ABCD是中心对称图形,直线EF经过对称中心O,则S四边形AEFB
________S四边形DEFC(填“>”“<”“=”);
(2)正方形是中心对称图形,两个正方形如图②所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
总结反思、拓展升华
【课堂总结】
知识点:
1.中心对称图形、对称中心的概念.
2.中心对称的概念
3.成中心对称的图形的性质
(1)在成中心对称的两个图形中, 连结对应点的线段都经过对称中心, 且被对称中心平分.
(2)反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
注意事项:
五、【作业布置】
【知识技能类作业】
必做题:
1.下列图案中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列说法中,正确的是( )
A.在成中心对称的图形中,连结对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连结对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点,那么这两个图形一定关于这一点成中心对称
D.以上说法都正确
3.如图,在每个小正方形的边长均相等的网格中,△ABC的顶点及点O均在格点(网格线的交点)上.
(1)画出△ABC关于点O成中心对称的△A'B'C'.(点A、B、C的对应点分别为点A'、B'、C')
(2)将(1)中的△A'B'C'绕点A'顺时针旋转90°得到△A'B″C″,画出△A'B″C″.(点B'、C'的对应点分别为点B″、C″)
选做题:
4.如图,点M为线段EF的中点,△AEC与△BFD成中心对称,A、E、M、F、B共线,试确定对称中心,并指出图中相等的线段和相等的角.
5.如图,在△ABC中,∠ACB=90°,△ABC旋转后能与△DEC重合,且点B、C、E三点在同一直线上.
(1)图中旋转中心是哪一点?
(2)旋转角的度数是多少?
(3)DE和AB有怎样的位置关系?
【综合拓展类作业】
6.如图,在△ABC中,AD是BC边上的中线,△A'BD与△ACD关于点D成中心对称.
(1)直接写出图中所有相等的线段;
(2)若AB=5,AC=3,求线段AD长度的取值范围.
答案:
自学测试:
1.D 2.B 3.A
课堂巩固:
1.B;2.B;
3. 【解析】如图所示,点O,W分别为(1)(2)组两个图形的对称中心.
4.D;
5. 【解析】作法如下:
图中A的对应点是D,B的对应点是E,C的对应点是F;AB对应线段是DE,BC对应线段是EF,CD对应线段是AF.
6. 【解析】如图所示,BB',CC'的交点即为O,△A'B'C'即为所求.
7.2;
8. 【解析】(1)如题图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB=S四边形DEFC;
答案:=
(2)如图所示:
(3)如图所示:
作业布置:
参考答案
1.C 2.B
3.
4.旋转中心为点M.
相等的线段为AC=BD,CE=DF,AE=BF,EM=FM,AM=BM,AF=BE,
相等的角为∠A=∠B,∠C=∠D,∠CEA=∠DFB,∠CEF=∠DFE.
5.(1)旋转中心是点C.
(2)旋转角的度数是180°.
(3)DE和AB的位置关系是平行.
6.(1)BD=CD,AD=A'D,AC=A'B.
(2)1<AD<4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第9章轴对称、平移与旋转
9.4 中心对称
学习目标与重难点
学习目标:
1.能说出中心对称的定义并指出对称中心;能运用中心对称性质作出简单图形的对称点;
2. 通过 “观察特例→归纳定义→验证性质→规范作图” 的探究过程,发展几何直观与逻辑推理能力,体会从特殊到一般的数学思维。
3. 发现中心对称在艺术设计、建筑结构中的对称美,体会数学对现实世界的规律提炼作用,增强 “用数学眼光欣赏生活” 的意识。
学习重点: 1. 中心对称的概念理解:明确 “中心对称图形” 与 “两图形成中心对称” 的区别与联系;掌握对称中心的核心作用 —— 所有对称点连线的中点。
2. 中心对称的作图方法:熟练运用 “延长法” 作出对称点.
学习难点:中心对称性质的综合应用,在复杂情境中,能逆向运用 “对称点连线被对称中心平分” 的性质解决问题。
预习自测
知识链接
1.中心对称图形是旋转对称图形吗?
2.在线段、直角、正方形、长方形、正五边形中,是中心对称图形的有哪些?
3.如何确定对称中心?
自学自测
1.将图中所示的图案以圆心为中心,旋转180°后得到的图案是 ( )
A B C D
2.下列四个2024年巴黎奥运会项目图标中,不是中心对称图形的是 ( )
A B C D
3.在如图所示的4组图形中,右边的图形与左边的图形成中心对称的是 ( )
A B C D
教学过程
一、创设情境、导入新课
1.旋转对称图形的定义:一个图形绕着某个定点,旋转一定的角度后能与自身重合,这样的图形叫做旋转对称图形.
在上一节中, 我们已经看到有不少图形绕着某一中心旋转一定角度后,可以与自身重合.如图9.4.1所示的三个图形是这样的旋转对称图形吗?请指出它们的旋转角度是多少?
二、合作交流、新知探究
探究一: 中心对称图形的认识
教材第149页:
问题1:将下面的图形绕O点旋转180°,你有什么发现?
提取概念:
中心对称图形:
_______________________________________________________________________________________
_______________________________________________________________________________________
对称中心:
_______________________________________________________________________________________
中心对称图形是旋转角度为180°的旋转对称图形,你能举出一些这样的实例吗?
问题2:观察下列图形的运动,说一说它们有什么共同点.
思考:线段、三角形、平行四边形、正方形、圆分别是中心对称图形吗?如果是,那么对称中心又分别在哪里?
探究二:成中心对称的图形的特征
教材第149页:
探索1:如图9.4.2,△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,点B关于对称中心A的对称点为___,点C关于对称中心A的对称点是____,点A关于对称中心A的对称点为____.
点B绕着点A旋转180°到达点D处,因此B、A、D 三点在同一条直线上,并且AD=AB.
思考:C、A、E三点的位置关系怎样?线段 AC、AE的大小关系呢?
探索2:在图9.4.3中,△A'B'C'与△ABC 关于点O成中心对称.你能从图中找到哪些等量关系?
归纳总结:在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
探究三:例题讲解
例 如图9.4.4,已知△ABC和点O,作△DEF,使△DEF与△ABC关于点O成中心对称.
试一试:如图9.4.6,所示的两个图形成中心对称, 你能找到它们的对称中心吗?
小明找到了如图 9.4.7 所示的方法, 你呢? 你知道其中的理由吗? 你还能找到其他方法吗?
做一做:如图 9.4.8, 在纸上作△ABC 和点 O, 以及过点 O 的任意两条互相垂直的直线 x、 y, 作出△ABC 关于直线x对称的△A′B′C′, 再作出△A′B′C′关于直线y对称的△A″B″C″.
观察△ABC 和△A″B″C″, 你能发现这两个三角形有什么关系吗?
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.剪纸是中国传统的民间艺术,下列各剪纸图案中,不是中心对称图形的是( )
2.下列命题中:
①中心对称图形一定是轴对称图形;②有两条互相垂直的对称轴的轴对称图形一定是中心对称图形;③关于某一点为中心对称的两个三角形能重合;④两个重合的图形一定为中心对称.其中正确的个数为( )
A.1 B.2 C.3 D.4
3.已知每组中的两个图形分别关于某点成中心对称,画出对称中心.
选做题:
4.下列各组图形中,△A'B'C'与△ABC成中心对称的是( )
5.已知六边形ABCDEF是以O为中心的中心对称图形(如图),画出六边形ABCDEF的全部图形,并指出所有的对应点和对应线段.
6.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
【综合拓展类作业】
7.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成中心对称且也以格点为顶点的三角形共有 ;(不包括△ABC本身)
8.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,四边形ABCD是中心对称图形,直线EF经过对称中心O,则S四边形AEFB
________S四边形DEFC(填“>”“<”“=”);
(2)正方形是中心对称图形,两个正方形如图②所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
总结反思、拓展升华
【课堂总结】
知识点:
1.中心对称图形、对称中心的概念.
2.中心对称的概念
3.成中心对称的图形的性质
(1)在成中心对称的两个图形中, 连结对应点的线段都经过对称中心, 且被对称中心平分.
(2)反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
注意事项:
五、【作业布置】
【知识技能类作业】
必做题:
1.下列图案中,既是轴对称图形又是中心对称图形的是( )
A B C D
2.下列说法中,正确的是( )
A.在成中心对称的图形中,连结对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连结对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点,那么这两个图形一定关于这一点成中心对称
D.以上说法都正确
3.如图,在每个小正方形的边长均相等的网格中,△ABC的顶点及点O均在格点(网格线的交点)上.
(1)画出△ABC关于点O成中心对称的△A'B'C'.(点A、B、C的对应点分别为点A'、B'、C')
(2)将(1)中的△A'B'C'绕点A'顺时针旋转90°得到△A'B″C″,画出△A'B″C″.(点B'、C'的对应点分别为点B″、C″)
选做题:
4.如图,点M为线段EF的中点,△AEC与△BFD成中心对称,A、E、M、F、B共线,试确定对称中心,并指出图中相等的线段和相等的角.
5.如图,在△ABC中,∠ACB=90°,△ABC旋转后能与△DEC重合,且点B、C、E三点在同一直线上.
(1)图中旋转中心是哪一点?
(2)旋转角的度数是多少?
(3)DE和AB有怎样的位置关系?
【综合拓展类作业】
6.如图,在△ABC中,AD是BC边上的中线,△A'BD与△ACD关于点D成中心对称.
(1)直接写出图中所有相等的线段;
(2)若AB=5,AC=3,求线段AD长度的取值范围.
答案:
自学测试:
1.D 2.B 3.A
课堂巩固:
1.B;2.B;
3. 【解析】如图所示,点O,W分别为(1)(2)组两个图形的对称中心.
4.D;
5. 【解析】作法如下:
图中A的对应点是D,B的对应点是E,C的对应点是F;AB对应线段是DE,BC对应线段是EF,CD对应线段是AF.
6. 【解析】如图所示,BB',CC'的交点即为O,△A'B'C'即为所求.
7.2;
8. 【解析】(1)如题图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB=S四边形DEFC;
答案:=
(2)如图所示:
(3)如图所示:
作业布置:
参考答案
1.C 2.B
3.
4.旋转中心为点M.
相等的线段为AC=BD,CE=DF,AE=BF,EM=FM,AM=BM,AF=BE,
相等的角为∠A=∠B,∠C=∠D,∠CEA=∠DFB,∠CEF=∠DFE.
5.(1)旋转中心是点C.
(2)旋转角的度数是180°.
(3)DE和AB的位置关系是平行.
6.(1)BD=CD,AD=A'D,AC=A'B.
(2)1<AD<4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
