华师大版七下(2024版)9.5图形的全等课件
文档属性
| 名称 | 华师大版七下(2024版)9.5图形的全等课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 00:00:00 | ||
图片预览











文档简介
(共42张PPT)
第九章 轴对称、平移与旋转
9.5图形的全等
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能准确阐述全等图形的定义,识别生活与数学情境中的全等图形,并用符号 “≌” 规范表示全等关系; 熟练运用全等图形的性质和判定,根据图形变换类型确定对应边、对应角,解决简单的线段长度、角度计算问题.
01
通过 “观察实例 — 操作验证 — 归纳性质 — 应用拓展” 的探究过程,经历从具体到抽象的数学建模活动,提升几何直观能力与逻辑推理能力,掌握 “从特殊到一般” 的数学研究方法。
02
感受全等图形在建筑设计、艺术创作、工业生产中的美学价值与实用价值,体会数学与生活的紧密联系,增强用数学眼光观察世界、用数学思维解决问题的信心。
03
02
新知导入
1.图形的轴对称、平移和旋转,这是图形的三种基本变换有什么共同点呢?
2.下列各组图形的形状与大小有什么特点?
图形经过这样的变换,位置发生了改变,但变换前后两个图形的对应线段相等,对应角相等,图形的形状和大小并没有改变.
形状大小相同
03
新知探究
问题1:观察思考:每组中的两个图形有什么特点?
探究一
全等图形的认识
形状大小完全相同
03
新知探究
问题2:观察思考:每组中的两个图形有什么特点?
探究一
全等图形的认识
形状大小完全相同
03
新知探究
我们已经认识了图形的轴对称、平移与旋转,这是图形的三种基本变换,图形经过这样的变换,位置发生了改变,但变换前后两个图形的对应线段相等,对应角相等,图形的形状和大小并没有改变.
03
新知探究
要想知道两个图形的形状和大小是否完全相同,可以通过轴对称、平移与旋转这些图形的变换,把两个图形叠合在一起,观察它们是否完全重合.能够完全重合的两个图形叫做全等图形.
概括
03
新知探究
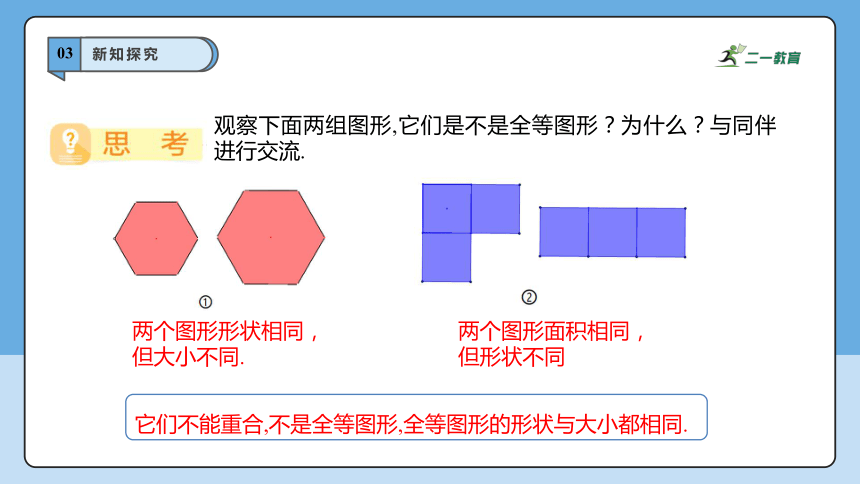
观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流.
两个图形形状相同,但大小不同.
两个图形面积相同,但形状不同
它们不能重合,不是全等图形,全等图形的形状与大小都相同.
03
新知探究
轴对称、 平移与旋转都是从实际生活中抽象得到的一些基本变换, 它们保证了变换过程中, 任意两点之间的距离不变, 从而保证了图形的形状和大小都不发生变化, 反映了图形之间的全等关系. 这种运用动态变换研究图形之间关系的方法, 是一种重要而且有效的方法.
03
新知探究
图9.5.1中给出了8个图形,你能发现哪两个图形是全等图形吗 动手试试看.
全等图形:
(2)和(4) (3)和(6)
一个图形经过轴对称、平移和旋转等变换所得到的新图形一定与原图形全等;
反过来,两个全等的图形经过上述变换后一定能够互相重合.
03
新知探究
1.两个能够完全重合的图形称为全等图形.
2.图形经过轴对称、平移或旋转等变换所得到的新图形一定与原图形全等.
3.两个全等图形经过轴对称、平移或旋转等变换后一定能够互相重合.
概括
03
新知探究
思考:观察图9.5.2中的两对多边形,每对中的其中一个可以经过怎样的变换和另一个图形重合?
探究二
全等图形的性质和判定
03
新知探究
探究二
全等图形的性质和判定
左图中可绕点O逆时针旋转90°后重合.
03
新知探究
探究二
全等图形的性质和判定
右图中可向下平移三格,再沿直线作轴对称即可重合.
03
新知探究
两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
概括
03
新知探究
如下图9.5.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′(这里,符号“≌”表示全等,读作“全等于”). 点A与点A′、点B与点B′、点C与点C′、点D与点D′、点E与点E′分别是对应顶点.
思考:请指出两个图形的对应角和对应边.
对应角:∠A与∠A' ∠B与∠B' ∠C与∠C' ∠D与∠D' ∠E与∠E'
对应边:AB=A'B' BC=B'C' CD=C'D' DE=D'E' EA=E'A'
03
新知探究
1.全等多边形的性质:全等多边形的对应边相等,对应角相等.
2.全等多边形的判定方法:边、角分别对应相等的两个多边形称为全等多边形.
3.全等三角形的性质:全等三角形的对应边、对应角分别相等.
4.全等三角形的判定方法:如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
归纳总结
03
新知探究
解:对应顶点:点A与点D、点B与点E、点C与点F;
对应边: AB与DE、BC与EF、CA与ED;
对应角:∠A与∠D、∠B与∠E、∠C与∠F.
如图9.5.4所示,△ABC≌△DEF,且∠A=∠D,∠B=∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗?
04
例题讲解
如图9.5.5,△ABC沿着BC的方向平移至△DEF,∠A=80°,∠B=60°求∠F的度数.
例1
分析
通过平移后的两个三角形是全等三角形,全等三角形的对应边、对应角分别相等
04
例题讲解
解析
【解】由图形平移的特征,可知△ABC和△DEF的形状与大小相同,
即△ABC≌△DEF.
∴∠D=∠A=80°(全等三角形的对应角相等).
同理∠DEF=∠B=60°.
又∵∠D+∠DEF+∠F=180°(三角形的内角和等于180°),
∴∠F=180°∠D∠DEF180°80°60°40°.
04
新知讲解
全等三角形对应边相等,根据图形以及全等三角形对应顶点的字母写在对应位置上准确找出对应角是解题的关键.
方法总结
04
例题讲解
分析
(1)根据全等三角形对应边相等;
(2)由,且,代入数据进行计算即可得解.
如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=7.
(1)试说明AB=CD;
(2)求线段AB的长.
例2
04
例题讲解
解析
【解】(1),
,
,
即.
(2),且,
.
04
新知讲解
全等三角形对应边相等,根据图形以及全等三角形对应顶点的字母写在对应位置上准确找出对应边是解题的关键.
方法总结
1.下列四个图形中,属于全等图形的是( )
A.①和② B.②和③ C.①和③ D.全部
04
课堂练习
【知识技能类作业】必做题:
A
2.如图,直角△ABC沿直角边BC所在直线向右平移到直角△DEF,则下列结论中,错误的是( )
A.BE=EC B.BC=EF C.AC=DF D.△ABC≌△DEF
A
3.若△ABC≌△A'B'C',且∠C=50°,∠BAC-∠A'B'C'=10°,则∠BAC= .
4.如图所示,△ABC与△DEC全等,且∠ACB=90°.
(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角;
(2)请直接写出直线AB,DE的位置关系.
04
课堂练习
【知识技能类作业】必做题:
70°
解:(1)△ABC与△DEC全等,观察题中图形发现可将△ABC绕点C顺时针旋转90°得到△DEC(答案不唯一).
对应边:AB与DE,AC与DC,BC与EC,
对应角:∠A与∠D,∠ACB与∠DCE,∠ABC与∠E.
(2)直线AB,DE互相垂直.
04
课堂练习
【知识技能类作业】选做题:
D
48
5.在直角三角形ABC中,D,E分别是AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠C=( )
A.15° B.20° C.25° D.30°
6.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为 .
04
课堂练习
【知识技能类作业】选做题:
解:(1)因为所以
因为,所以,
所以
即的度数为;
(2)因为,
所以,
所以与的周长和为.
7.如图,,点在边上,与交于点,已知.
(1)求的度数.
(2)求与的周长和.
04
课堂练习
【综合拓展类作业】
8.如图①,在直角△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为t s.
(1)如图①,当t= 时,△APC的面积等于△ABC面积的一半;
(2)如图②,在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
04
课堂练习
【综合拓展类作业】
(1)①当点P在BC上时,如图①-1所示,
若△APC的面积等于△ABC面积的一半;则CP=BC= cm,
此时,点P移动的距离为AC+CP=12+=(cm),
移动的时间为:÷3=(s),
②当点P在BA上时,如图①-2所示,
若△APC的面积等于△ABC面积的一半;则PB=AB= cm,即点P为BA的中点,
此时,点P移动的距离为AC+CB+BP=12+9+=(cm),
移动的时间为:÷3=(s);
答案:或
04
课堂练习
【综合拓展类作业】
(2)△APQ≌△DEF,即对应顶点为A与D,P与E,Q与F;
①当点P在AC上时,如图②-1所示,
此时,AP=4,AQ=5,
所以点Q移动的速度为5÷(4÷3)= cm/s,
②当点P在AB上时,如图②-2所示,此时,AP=4,AQ=5,
即点P移动的距离为9+12+15-4=32(cm),点Q移动的距离为9+12+15-5=31(cm),
所以点Q移动的速度为31÷(32÷3)= cm/s,
综上所述,在两点运动过程中的某一时刻,恰好△APQ≌△DEF,点Q的运动速度为 cm/s或 cm/s.
05
课堂小结
全等图形
能够完全重合的图形.
定义
性质:对应边,角分别相等
判定方法:边,角分别对应相等,则三角形全等
全等三角形
对应角相等,对应边相等.
性质
2.如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中不一定正确的是( )
A.BE=EC B.BC=EF C.AC=DF D.△ABC≌△DEF
1.下列四个图形中,有两个全等的图形,它们是( )
A.①和② B.②和③ C.②和④ D.③和④
06
作业布置
【知识技能类作业】必做题:
B
A
3.如图,已知△ABC≌△BAD.若∠DAC=20°,∠C=88°,则∠DBA= °.
06
作业布置
【知识技能类作业】必做题:
36
4.如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,则∠DFE= °,EC= .
100
2
06
作业布置
【知识技能类作业】选做题:
5.如图,△ABC≌△DEF,点B、E、C、F在同一条直线上.
(1)若∠BED=140°,∠D=75°,求∠ACB的度数;
(2)若BE=2,EC=3,求BF的长.
解(1).,.
又,
.
.
(2),.
又,
.
.
06
作业布置
【知识技能类作业】选做题:
解(1).
.
.
(2),
.
.
6.如图,已知.
(1)若,求线段的长;
(2)若求的度数.
06
作业布置
【知识技能类作业】选做题:
解(1).
.
.
(2),
.
.
.
7.如图,已知,点在上,与相交于点,若
(1)求线段的长;
(2)求的度数.
06
作业布置
【综合拓展类作业】
8.如图1,已知△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,C为AD的中点.
(1)求∠BAE的度数和AE的长;
解(1).
.
.
为的中点,
,
.
06
作业布置
【综合拓展类作业】
解(2).
.
.
(2)如图2,延长BC,交ED于点F,求∠DFC的度数.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第九章 轴对称、平移与旋转
9.5图形的全等
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能准确阐述全等图形的定义,识别生活与数学情境中的全等图形,并用符号 “≌” 规范表示全等关系; 熟练运用全等图形的性质和判定,根据图形变换类型确定对应边、对应角,解决简单的线段长度、角度计算问题.
01
通过 “观察实例 — 操作验证 — 归纳性质 — 应用拓展” 的探究过程,经历从具体到抽象的数学建模活动,提升几何直观能力与逻辑推理能力,掌握 “从特殊到一般” 的数学研究方法。
02
感受全等图形在建筑设计、艺术创作、工业生产中的美学价值与实用价值,体会数学与生活的紧密联系,增强用数学眼光观察世界、用数学思维解决问题的信心。
03
02
新知导入
1.图形的轴对称、平移和旋转,这是图形的三种基本变换有什么共同点呢?
2.下列各组图形的形状与大小有什么特点?
图形经过这样的变换,位置发生了改变,但变换前后两个图形的对应线段相等,对应角相等,图形的形状和大小并没有改变.
形状大小相同
03
新知探究
问题1:观察思考:每组中的两个图形有什么特点?
探究一
全等图形的认识
形状大小完全相同
03
新知探究
问题2:观察思考:每组中的两个图形有什么特点?
探究一
全等图形的认识
形状大小完全相同
03
新知探究
我们已经认识了图形的轴对称、平移与旋转,这是图形的三种基本变换,图形经过这样的变换,位置发生了改变,但变换前后两个图形的对应线段相等,对应角相等,图形的形状和大小并没有改变.
03
新知探究
要想知道两个图形的形状和大小是否完全相同,可以通过轴对称、平移与旋转这些图形的变换,把两个图形叠合在一起,观察它们是否完全重合.能够完全重合的两个图形叫做全等图形.
概括
03
新知探究
观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流.
两个图形形状相同,但大小不同.
两个图形面积相同,但形状不同
它们不能重合,不是全等图形,全等图形的形状与大小都相同.
03
新知探究
轴对称、 平移与旋转都是从实际生活中抽象得到的一些基本变换, 它们保证了变换过程中, 任意两点之间的距离不变, 从而保证了图形的形状和大小都不发生变化, 反映了图形之间的全等关系. 这种运用动态变换研究图形之间关系的方法, 是一种重要而且有效的方法.
03
新知探究
图9.5.1中给出了8个图形,你能发现哪两个图形是全等图形吗 动手试试看.
全等图形:
(2)和(4) (3)和(6)
一个图形经过轴对称、平移和旋转等变换所得到的新图形一定与原图形全等;
反过来,两个全等的图形经过上述变换后一定能够互相重合.
03
新知探究
1.两个能够完全重合的图形称为全等图形.
2.图形经过轴对称、平移或旋转等变换所得到的新图形一定与原图形全等.
3.两个全等图形经过轴对称、平移或旋转等变换后一定能够互相重合.
概括
03
新知探究
思考:观察图9.5.2中的两对多边形,每对中的其中一个可以经过怎样的变换和另一个图形重合?
探究二
全等图形的性质和判定
03
新知探究
探究二
全等图形的性质和判定
左图中可绕点O逆时针旋转90°后重合.
03
新知探究
探究二
全等图形的性质和判定
右图中可向下平移三格,再沿直线作轴对称即可重合.
03
新知探究
两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
概括
03
新知探究
如下图9.5.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′(这里,符号“≌”表示全等,读作“全等于”). 点A与点A′、点B与点B′、点C与点C′、点D与点D′、点E与点E′分别是对应顶点.
思考:请指出两个图形的对应角和对应边.
对应角:∠A与∠A' ∠B与∠B' ∠C与∠C' ∠D与∠D' ∠E与∠E'
对应边:AB=A'B' BC=B'C' CD=C'D' DE=D'E' EA=E'A'
03
新知探究
1.全等多边形的性质:全等多边形的对应边相等,对应角相等.
2.全等多边形的判定方法:边、角分别对应相等的两个多边形称为全等多边形.
3.全等三角形的性质:全等三角形的对应边、对应角分别相等.
4.全等三角形的判定方法:如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
归纳总结
03
新知探究
解:对应顶点:点A与点D、点B与点E、点C与点F;
对应边: AB与DE、BC与EF、CA与ED;
对应角:∠A与∠D、∠B与∠E、∠C与∠F.
如图9.5.4所示,△ABC≌△DEF,且∠A=∠D,∠B=∠E.你能指出它们之间其他的对应顶点、对应角和对应边吗?
04
例题讲解
如图9.5.5,△ABC沿着BC的方向平移至△DEF,∠A=80°,∠B=60°求∠F的度数.
例1
分析
通过平移后的两个三角形是全等三角形,全等三角形的对应边、对应角分别相等
04
例题讲解
解析
【解】由图形平移的特征,可知△ABC和△DEF的形状与大小相同,
即△ABC≌△DEF.
∴∠D=∠A=80°(全等三角形的对应角相等).
同理∠DEF=∠B=60°.
又∵∠D+∠DEF+∠F=180°(三角形的内角和等于180°),
∴∠F=180°∠D∠DEF180°80°60°40°.
04
新知讲解
全等三角形对应边相等,根据图形以及全等三角形对应顶点的字母写在对应位置上准确找出对应角是解题的关键.
方法总结
04
例题讲解
分析
(1)根据全等三角形对应边相等;
(2)由,且,代入数据进行计算即可得解.
如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=7.
(1)试说明AB=CD;
(2)求线段AB的长.
例2
04
例题讲解
解析
【解】(1),
,
,
即.
(2),且,
.
04
新知讲解
全等三角形对应边相等,根据图形以及全等三角形对应顶点的字母写在对应位置上准确找出对应边是解题的关键.
方法总结
1.下列四个图形中,属于全等图形的是( )
A.①和② B.②和③ C.①和③ D.全部
04
课堂练习
【知识技能类作业】必做题:
A
2.如图,直角△ABC沿直角边BC所在直线向右平移到直角△DEF,则下列结论中,错误的是( )
A.BE=EC B.BC=EF C.AC=DF D.△ABC≌△DEF
A
3.若△ABC≌△A'B'C',且∠C=50°,∠BAC-∠A'B'C'=10°,则∠BAC= .
4.如图所示,△ABC与△DEC全等,且∠ACB=90°.
(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角;
(2)请直接写出直线AB,DE的位置关系.
04
课堂练习
【知识技能类作业】必做题:
70°
解:(1)△ABC与△DEC全等,观察题中图形发现可将△ABC绕点C顺时针旋转90°得到△DEC(答案不唯一).
对应边:AB与DE,AC与DC,BC与EC,
对应角:∠A与∠D,∠ACB与∠DCE,∠ABC与∠E.
(2)直线AB,DE互相垂直.
04
课堂练习
【知识技能类作业】选做题:
D
48
5.在直角三角形ABC中,D,E分别是AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠C=( )
A.15° B.20° C.25° D.30°
6.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为 .
04
课堂练习
【知识技能类作业】选做题:
解:(1)因为所以
因为,所以,
所以
即的度数为;
(2)因为,
所以,
所以与的周长和为.
7.如图,,点在边上,与交于点,已知.
(1)求的度数.
(2)求与的周长和.
04
课堂练习
【综合拓展类作业】
8.如图①,在直角△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为t s.
(1)如图①,当t= 时,△APC的面积等于△ABC面积的一半;
(2)如图②,在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
04
课堂练习
【综合拓展类作业】
(1)①当点P在BC上时,如图①-1所示,
若△APC的面积等于△ABC面积的一半;则CP=BC= cm,
此时,点P移动的距离为AC+CP=12+=(cm),
移动的时间为:÷3=(s),
②当点P在BA上时,如图①-2所示,
若△APC的面积等于△ABC面积的一半;则PB=AB= cm,即点P为BA的中点,
此时,点P移动的距离为AC+CB+BP=12+9+=(cm),
移动的时间为:÷3=(s);
答案:或
04
课堂练习
【综合拓展类作业】
(2)△APQ≌△DEF,即对应顶点为A与D,P与E,Q与F;
①当点P在AC上时,如图②-1所示,
此时,AP=4,AQ=5,
所以点Q移动的速度为5÷(4÷3)= cm/s,
②当点P在AB上时,如图②-2所示,此时,AP=4,AQ=5,
即点P移动的距离为9+12+15-4=32(cm),点Q移动的距离为9+12+15-5=31(cm),
所以点Q移动的速度为31÷(32÷3)= cm/s,
综上所述,在两点运动过程中的某一时刻,恰好△APQ≌△DEF,点Q的运动速度为 cm/s或 cm/s.
05
课堂小结
全等图形
能够完全重合的图形.
定义
性质:对应边,角分别相等
判定方法:边,角分别对应相等,则三角形全等
全等三角形
对应角相等,对应边相等.
性质
2.如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中不一定正确的是( )
A.BE=EC B.BC=EF C.AC=DF D.△ABC≌△DEF
1.下列四个图形中,有两个全等的图形,它们是( )
A.①和② B.②和③ C.②和④ D.③和④
06
作业布置
【知识技能类作业】必做题:
B
A
3.如图,已知△ABC≌△BAD.若∠DAC=20°,∠C=88°,则∠DBA= °.
06
作业布置
【知识技能类作业】必做题:
36
4.如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,则∠DFE= °,EC= .
100
2
06
作业布置
【知识技能类作业】选做题:
5.如图,△ABC≌△DEF,点B、E、C、F在同一条直线上.
(1)若∠BED=140°,∠D=75°,求∠ACB的度数;
(2)若BE=2,EC=3,求BF的长.
解(1).,.
又,
.
.
(2),.
又,
.
.
06
作业布置
【知识技能类作业】选做题:
解(1).
.
.
(2),
.
.
6.如图,已知.
(1)若,求线段的长;
(2)若求的度数.
06
作业布置
【知识技能类作业】选做题:
解(1).
.
.
(2),
.
.
.
7.如图,已知,点在上,与相交于点,若
(1)求线段的长;
(2)求的度数.
06
作业布置
【综合拓展类作业】
8.如图1,已知△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,C为AD的中点.
(1)求∠BAE的度数和AE的长;
解(1).
.
.
为的中点,
,
.
06
作业布置
【综合拓展类作业】
解(2).
.
.
(2)如图2,延长BC,交ED于点F,求∠DFC的度数.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
