2024-2025学年北师大版九年级数学下册 2.4课时3 抛物线的实际问题 课件(共32张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册 2.4课时3 抛物线的实际问题 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 781.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 16:00:04 | ||
图片预览











文档简介
(共32张PPT)
第二章 二次函数
2.4 二次函数的应用
课时3 抛物线的实际问题
1.实际中二次函数模型的建立
2.求实际中“抛物线”型的最值问题. (重点、难点)
学习目标
新课导入
前面我们已经学习了利用二次函数解决几何最值问题,实际问题中最值问题,本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
新课讲解
1.运用二次函数的代数模型解决实际中的问题,如抛
(投)物体,抛物线的模型问题等,经常需要运用抽象
与概括的数学思想,将文字语言转化为数学符号.
新课讲解
2.利用二次函数解决实际问题的基本思路是:
(1)建立适当的平面直角坐标系;
(2)把实际问题中一些数据与点的坐标联系起来;
(3)用待定系数法求出抛物线对应的函数表达式;
(4)利用二次函数的图象及性质去分析、解决问题.
新课讲解
例
随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池(如图2-4-8),在水池中心竖直安装了一根高为2 m 的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1 m 处达到最高,水柱落地处离水池中心3 m.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线对应的函数表达式.
(2)求水柱的最大高度是多少.
新课讲解
解:
新课讲解
新课讲解
例
典例分析
如图,某灌溉设备的喷头B高出地面1.25 m,喷出的抛物线型水流在与喷头底部A的距离为1 m处达到距离地面最大高度2.25 m,试建立恰当的直角坐标系并求出与该抛物线型水流对应的二次函数关系式.
新课讲解
分析:解决问题的关键是建立适当的平面直角坐标系,把
实际问题中的长度转化为点的坐标,从而利用待定
系数法求二次函数关系式.
新课讲解
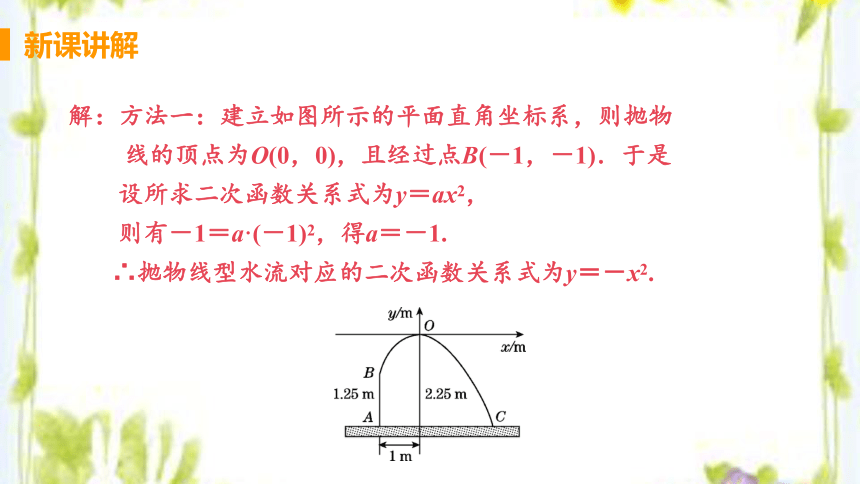
解:方法一:建立如图所示的平面直角坐标系,则抛物
线的顶点为O(0,0),且经过点B(-1,-1).于是
设所求二次函数关系式为y=ax2,
则有-1=a·(-1)2,得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2.
新课讲解
方法二:建立如图所示的平面直角坐标系,则抛物线的
顶点为D(0,2.25),且抛物线经过点B(-1,1.25).于是
设所求二次函数关系式为y=ax2+2.25,则有1.25=a·
(-1)2+2.25,解得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2+2.25.
新课讲解
方法三:建立如图所示的平面直角坐标系,则抛物线的
顶点为D(1,2.25),且经过点B(0,1.25).于是设所求二
次函数关系式为y=a(x-1)2+2.25,则有1.25=a(-1)2+
2.25,解得a=-1.∴抛物线型水流对应的二次函数关系
式为y=-(x-1)2+2.25.
课堂小结
1.抛物线型建筑物问题:几种常见的抛物线型建筑
物有拱形桥洞、隧道洞口、拱形门等.解决这类
问题的关键是根据已知条件选择合理的位置建立
直角坐标系,结合问题中的数据求出函数解析式,
然后利用函数解析式解决问题.
课堂小结
2.运动问题:(1)运动中的距离、时间、速度问题;
这类问题多根据运动规律中的公式求解.(2)物
体的运动路线(轨迹)问题;解决这类问题的思想
方法是利用数形结合思想和函数思想,合理建立
直角坐标系,根据已知数据,运用待定系数法求
出运动轨迹(抛物线)的解析式,再利用二次函数
的性质去分析、解决问题.
当堂小练
1.如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为 坐标原点时抛物线对应的函数表达式是y=- (x-6)2+4,则选取点B为坐标原点时抛物线对应的函数表达式是______________________.
当堂小练
2.向上发射一枚炮弹,经x s后的高度为y m,且时间与高度之间的关系为y=ax2+bx.若此炮弹在第7 s与第14 s时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9.5 s B.第10 s
C.第10.5 s D.第11 s
C
拓展与延伸
足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
拓展与延伸
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对称轴是直线t= ;③足球被踢出9 s时落地;④足球被踢出1.5 s时,距离地面的高度是11 m.其中正确结论的个数是( )
A.1 B.2
C.3 D.4
B
1.(人教9上P49、北师9下P41改编)(2024梅州一模)从地面竖直向上抛出一小球,小球的高度h(米)与运动时间t(秒)之间的关系式是h=-5t2+30t(0≤t≤6),则小球到达最高高度时,运动的时间是( )
A.1秒 B.2秒 C.3秒 D.4秒
C
课后练习
2.(人教9上P47改编)(2024辽宁一模)如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=-(x-10)(x+4),则铅球推出的距离OA= m.
10
3.(人教9上P49改编、北师9下P47改编)有一根长为20 cm的铁丝,把它弯成一个矩形ABCD,其中AB=x cm,矩形面积为y cm2.
(1)求y与x之间的函数关系式;
(2)当x为何值时,矩形的面积最大?最大面积为多少?
解:(1)∵AB=x,∴BC=10-x.
∴y=AB·BC=x(10-x)=-x2+10x,
其中0<x<10.
(2)y=-x2+10x=-(x-5)2+25.
∴当x=5时,矩形ABCD的面积最大,最大面积为25 cm2.
4.【例1】(跨学科融合)(人教9上P43改编、北师9下P52改编)如图,一个小球在地面O点被击出,球的飞行路线是抛物线y=-x2+x,其中y(m)是飞行高度,x(m)是球飞出的水平距离.
(1)求球飞行过程中的最大高度;
(2)求球飞行过程中的最远水平距离.
小结:(1)求最大高度的关键是求抛物线的顶点坐标;
(2)求最远水平距离的关键是求抛物线与x轴的交点坐标.
解:(1)球飞行过程中的最大高度就是抛物线y=-x2+x的顶点的纵坐标,由y=-x2+x=-(x-4)2+,知顶点坐标为,∴球飞行过程中的最大高度是 m.
(2)y=0时,即-x2+x=0,解得x1=0,x2=8.
∴球飞行过程中的最远水平距离是8 m.
5.【例2】(人教9上P57、北师9下P47)如图,用30 m长的篱笆沿墙建造一边靠墙的矩形菜园,已知墙长18 m,设矩形的宽AB为x m.
(1)用含x的代数式表示矩形的长BC;
(2)设矩形的面积为y m2,用含x的代数
式表示矩形的面积y,并求出自变量的取值范围;
(3)这个矩形菜园的长和宽各为多少时,菜园的面积y最大?最大面积是多少?
解:(1)∵AB=CD=x m,∴BC=(30-2x)m.
(2)由题意得y=x(30-2x)=-2x2+30x.
由x>0且0<30-2x≤18,解得6≤x<15.
(3)y=-2x2+30x=-2(x-7.5)2+112.5,
∴当x=7.5时,y有最大值,y最大=112.5,
此时这个矩形的长为15 m、宽为7.5 m.
答:这个矩形菜园的长为15 m、宽为7.5 m时,菜园的面积最大,最大面积是112.5 m2.
6.(跨学科融合)(2023襄阳改编)如图,一位篮球运动员投篮时,球从A点出手后沿抛物线行进,篮球出手后距离地面的高度y(m)与篮球距离出手点的水平距离x(m)之间的函数关系式是y=-x2+x+.
(1)求篮球出手点距离地面的高度;
(2)求篮球行进过程中距离地面的最大高度.
解:(1)令x=0,则y=,
故篮球出手点距离地面的高度为 m.
(2)∵y=-x2+x+=-,∴其顶点坐标为,故篮球行进过程中距离地面的最大高度为 m.
★7. 0.45 (北师9下P60改编)某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.
(1)当x为何值时,矩形花园的面积最大?最大面积为多少?
(2)若在P处有一棵树与墙CD,AD的距离分
别是15 m和6 m,要将这棵树围在花园内(含
边界,不考虑树的粗细),求花园面积S的最
大值.
解:(1)S=x(28-x)=-(x-14)2+196(0<x<28),
∵a=-1<0,
∴S有最大值,
当x=14时,S最大值=196(m2).
(2)依题意有,解得6≤x≤13,在对称轴的左侧,S随x的增大而增大,因此当x=13时,S最大值=195(m2).
请完成《 少年班 》本节对应习题
布置作业
感谢大家
第二章 二次函数
2.4 二次函数的应用
课时3 抛物线的实际问题
1.实际中二次函数模型的建立
2.求实际中“抛物线”型的最值问题. (重点、难点)
学习目标
新课导入
前面我们已经学习了利用二次函数解决几何最值问题,实际问题中最值问题,本节课我们继续学习利用二次函数解决拱桥、隧道、以及一些运动类的“抛物线”型问题.
新课讲解
1.运用二次函数的代数模型解决实际中的问题,如抛
(投)物体,抛物线的模型问题等,经常需要运用抽象
与概括的数学思想,将文字语言转化为数学符号.
新课讲解
2.利用二次函数解决实际问题的基本思路是:
(1)建立适当的平面直角坐标系;
(2)把实际问题中一些数据与点的坐标联系起来;
(3)用待定系数法求出抛物线对应的函数表达式;
(4)利用二次函数的图象及性质去分析、解决问题.
新课讲解
例
随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池(如图2-4-8),在水池中心竖直安装了一根高为2 m 的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1 m 处达到最高,水柱落地处离水池中心3 m.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线对应的函数表达式.
(2)求水柱的最大高度是多少.
新课讲解
解:
新课讲解
新课讲解
例
典例分析
如图,某灌溉设备的喷头B高出地面1.25 m,喷出的抛物线型水流在与喷头底部A的距离为1 m处达到距离地面最大高度2.25 m,试建立恰当的直角坐标系并求出与该抛物线型水流对应的二次函数关系式.
新课讲解
分析:解决问题的关键是建立适当的平面直角坐标系,把
实际问题中的长度转化为点的坐标,从而利用待定
系数法求二次函数关系式.
新课讲解
解:方法一:建立如图所示的平面直角坐标系,则抛物
线的顶点为O(0,0),且经过点B(-1,-1).于是
设所求二次函数关系式为y=ax2,
则有-1=a·(-1)2,得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2.
新课讲解
方法二:建立如图所示的平面直角坐标系,则抛物线的
顶点为D(0,2.25),且抛物线经过点B(-1,1.25).于是
设所求二次函数关系式为y=ax2+2.25,则有1.25=a·
(-1)2+2.25,解得a=-1.
∴抛物线型水流对应的二次函数关系式为y=-x2+2.25.
新课讲解
方法三:建立如图所示的平面直角坐标系,则抛物线的
顶点为D(1,2.25),且经过点B(0,1.25).于是设所求二
次函数关系式为y=a(x-1)2+2.25,则有1.25=a(-1)2+
2.25,解得a=-1.∴抛物线型水流对应的二次函数关系
式为y=-(x-1)2+2.25.
课堂小结
1.抛物线型建筑物问题:几种常见的抛物线型建筑
物有拱形桥洞、隧道洞口、拱形门等.解决这类
问题的关键是根据已知条件选择合理的位置建立
直角坐标系,结合问题中的数据求出函数解析式,
然后利用函数解析式解决问题.
课堂小结
2.运动问题:(1)运动中的距离、时间、速度问题;
这类问题多根据运动规律中的公式求解.(2)物
体的运动路线(轨迹)问题;解决这类问题的思想
方法是利用数形结合思想和函数思想,合理建立
直角坐标系,根据已知数据,运用待定系数法求
出运动轨迹(抛物线)的解析式,再利用二次函数
的性质去分析、解决问题.
当堂小练
1.如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为 坐标原点时抛物线对应的函数表达式是y=- (x-6)2+4,则选取点B为坐标原点时抛物线对应的函数表达式是______________________.
当堂小练
2.向上发射一枚炮弹,经x s后的高度为y m,且时间与高度之间的关系为y=ax2+bx.若此炮弹在第7 s与第14 s时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9.5 s B.第10 s
C.第10.5 s D.第11 s
C
拓展与延伸
足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
拓展与延伸
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对称轴是直线t= ;③足球被踢出9 s时落地;④足球被踢出1.5 s时,距离地面的高度是11 m.其中正确结论的个数是( )
A.1 B.2
C.3 D.4
B
1.(人教9上P49、北师9下P41改编)(2024梅州一模)从地面竖直向上抛出一小球,小球的高度h(米)与运动时间t(秒)之间的关系式是h=-5t2+30t(0≤t≤6),则小球到达最高高度时,运动的时间是( )
A.1秒 B.2秒 C.3秒 D.4秒
C
课后练习
2.(人教9上P47改编)(2024辽宁一模)如图,一名学生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=-(x-10)(x+4),则铅球推出的距离OA= m.
10
3.(人教9上P49改编、北师9下P47改编)有一根长为20 cm的铁丝,把它弯成一个矩形ABCD,其中AB=x cm,矩形面积为y cm2.
(1)求y与x之间的函数关系式;
(2)当x为何值时,矩形的面积最大?最大面积为多少?
解:(1)∵AB=x,∴BC=10-x.
∴y=AB·BC=x(10-x)=-x2+10x,
其中0<x<10.
(2)y=-x2+10x=-(x-5)2+25.
∴当x=5时,矩形ABCD的面积最大,最大面积为25 cm2.
4.【例1】(跨学科融合)(人教9上P43改编、北师9下P52改编)如图,一个小球在地面O点被击出,球的飞行路线是抛物线y=-x2+x,其中y(m)是飞行高度,x(m)是球飞出的水平距离.
(1)求球飞行过程中的最大高度;
(2)求球飞行过程中的最远水平距离.
小结:(1)求最大高度的关键是求抛物线的顶点坐标;
(2)求最远水平距离的关键是求抛物线与x轴的交点坐标.
解:(1)球飞行过程中的最大高度就是抛物线y=-x2+x的顶点的纵坐标,由y=-x2+x=-(x-4)2+,知顶点坐标为,∴球飞行过程中的最大高度是 m.
(2)y=0时,即-x2+x=0,解得x1=0,x2=8.
∴球飞行过程中的最远水平距离是8 m.
5.【例2】(人教9上P57、北师9下P47)如图,用30 m长的篱笆沿墙建造一边靠墙的矩形菜园,已知墙长18 m,设矩形的宽AB为x m.
(1)用含x的代数式表示矩形的长BC;
(2)设矩形的面积为y m2,用含x的代数
式表示矩形的面积y,并求出自变量的取值范围;
(3)这个矩形菜园的长和宽各为多少时,菜园的面积y最大?最大面积是多少?
解:(1)∵AB=CD=x m,∴BC=(30-2x)m.
(2)由题意得y=x(30-2x)=-2x2+30x.
由x>0且0<30-2x≤18,解得6≤x<15.
(3)y=-2x2+30x=-2(x-7.5)2+112.5,
∴当x=7.5时,y有最大值,y最大=112.5,
此时这个矩形的长为15 m、宽为7.5 m.
答:这个矩形菜园的长为15 m、宽为7.5 m时,菜园的面积最大,最大面积是112.5 m2.
6.(跨学科融合)(2023襄阳改编)如图,一位篮球运动员投篮时,球从A点出手后沿抛物线行进,篮球出手后距离地面的高度y(m)与篮球距离出手点的水平距离x(m)之间的函数关系式是y=-x2+x+.
(1)求篮球出手点距离地面的高度;
(2)求篮球行进过程中距离地面的最大高度.
解:(1)令x=0,则y=,
故篮球出手点距离地面的高度为 m.
(2)∵y=-x2+x+=-,∴其顶点坐标为,故篮球行进过程中距离地面的最大高度为 m.
★7. 0.45 (北师9下P60改编)某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.
(1)当x为何值时,矩形花园的面积最大?最大面积为多少?
(2)若在P处有一棵树与墙CD,AD的距离分
别是15 m和6 m,要将这棵树围在花园内(含
边界,不考虑树的粗细),求花园面积S的最
大值.
解:(1)S=x(28-x)=-(x-14)2+196(0<x<28),
∵a=-1<0,
∴S有最大值,
当x=14时,S最大值=196(m2).
(2)依题意有,解得6≤x≤13,在对称轴的左侧,S随x的增大而增大,因此当x=13时,S最大值=195(m2).
请完成《 少年班 》本节对应习题
布置作业
感谢大家
