人教版数学八上课件11.3.2多边形的内角和、外角和 (共47张PPT)
文档属性
| 名称 | 人教版数学八上课件11.3.2多边形的内角和、外角和 (共47张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-13 00:00:00 | ||
图片预览





文档简介
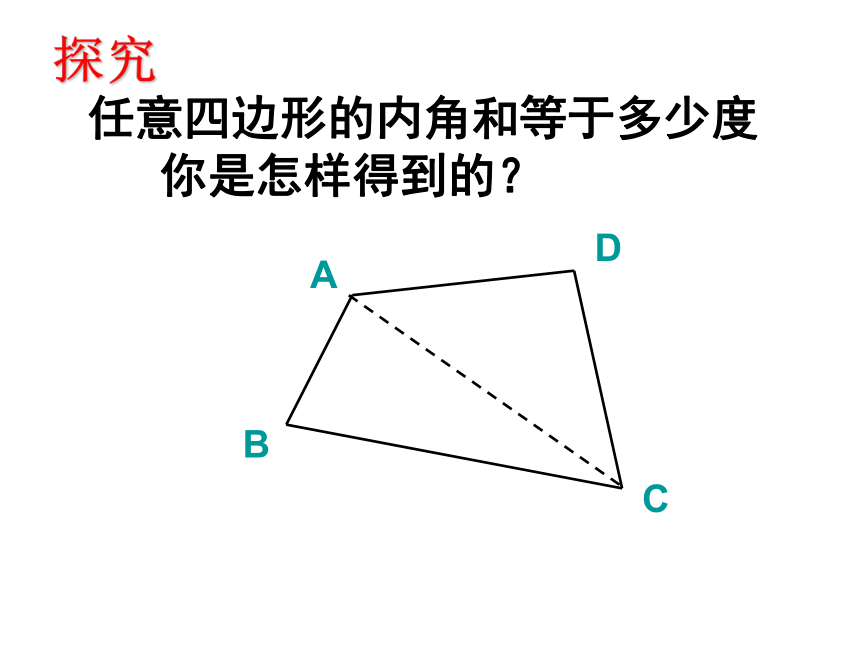
课件47张PPT。多边形及其内外角和三角形的内角和是180°,那么四边形的内角和是多少呢?五边形呢?你是如何得到这个结论的? 任意四边形的内角和等于多少度
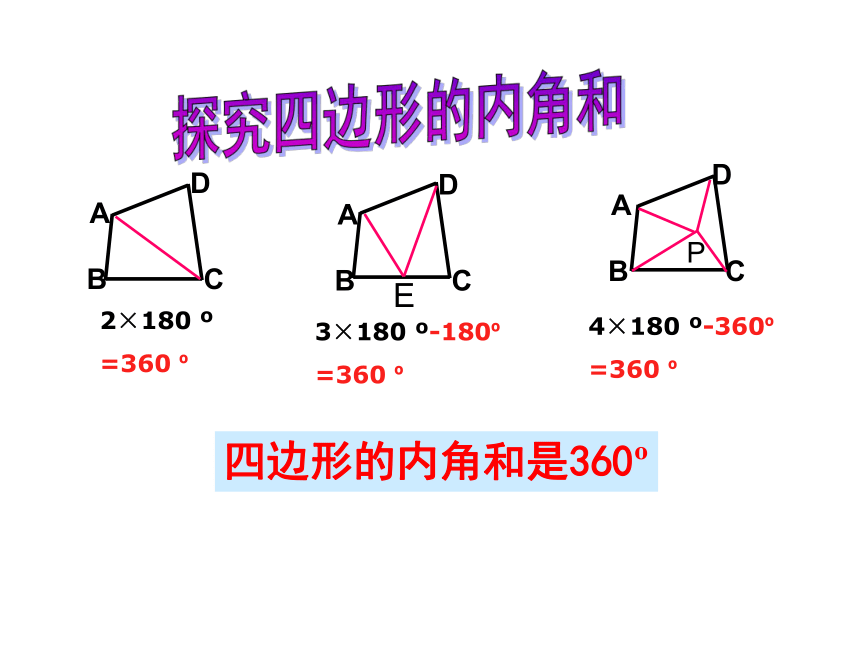
你是怎样得到的?ABCD探究探究四边形的内角和2×180 o
=360 o4×180 o-360o
=360 o四边形的内角和是360o3×180 o-180o
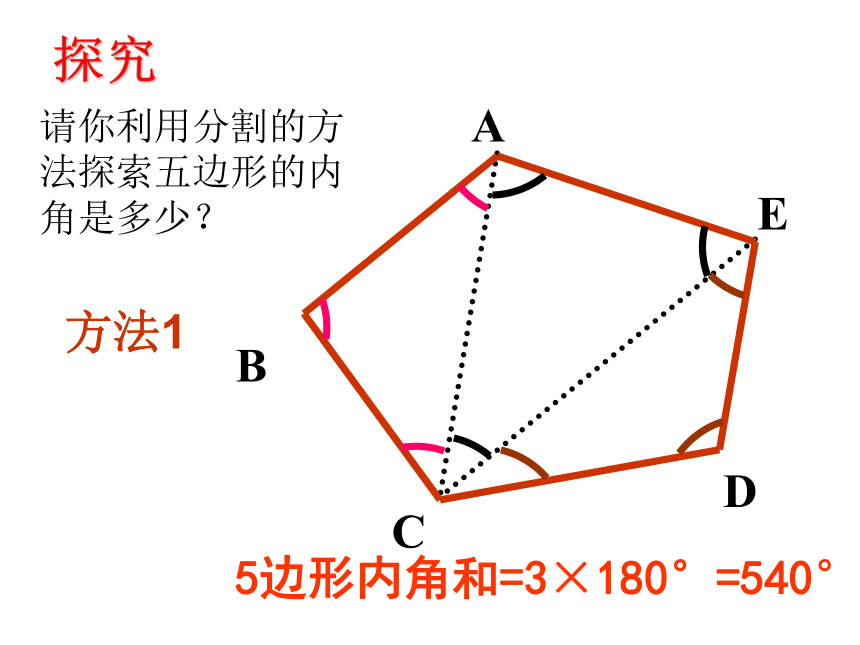
=360 oEP B ACDE探究5边形内角和=3×180°=540°请你利用分割的方法探索五边形的内角是多少?方法1E
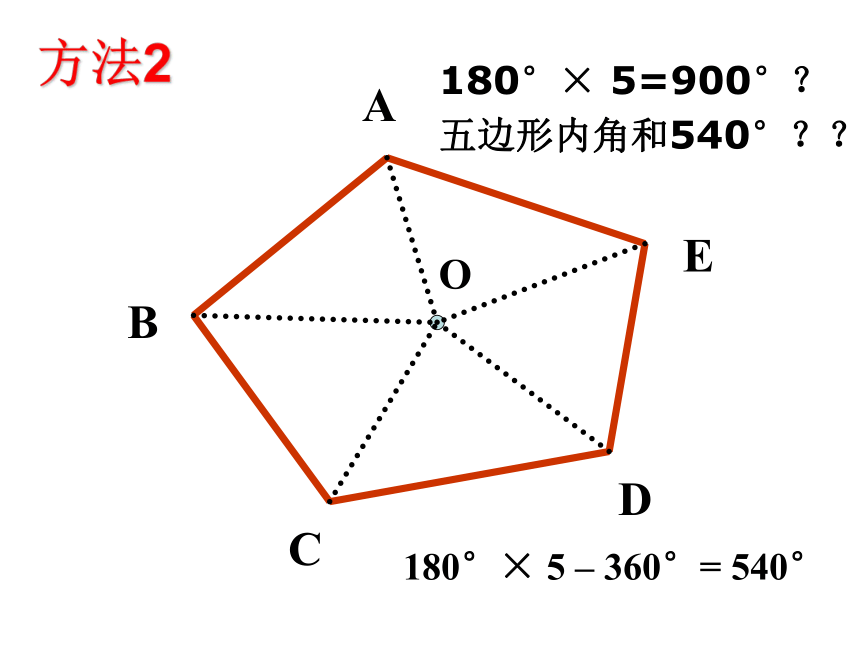
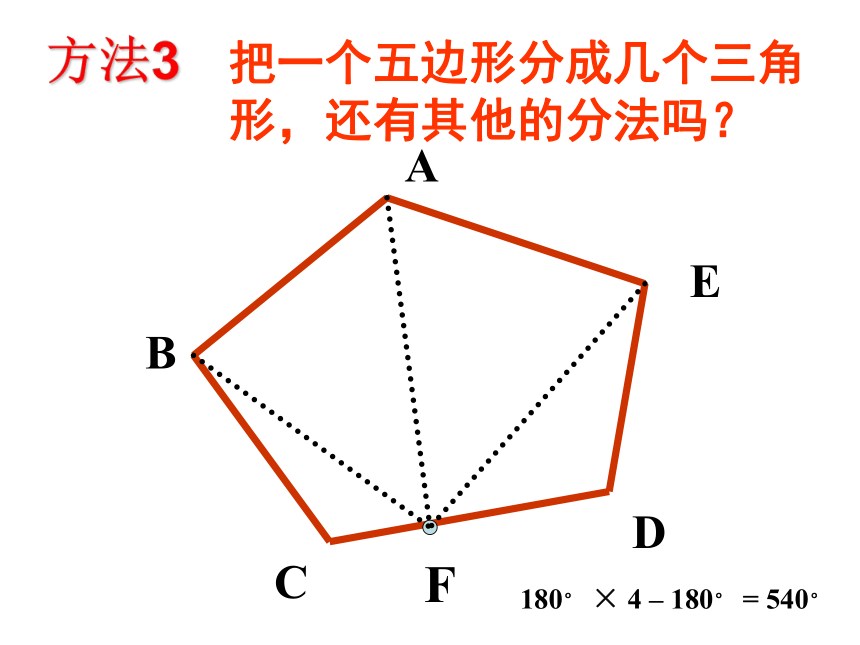
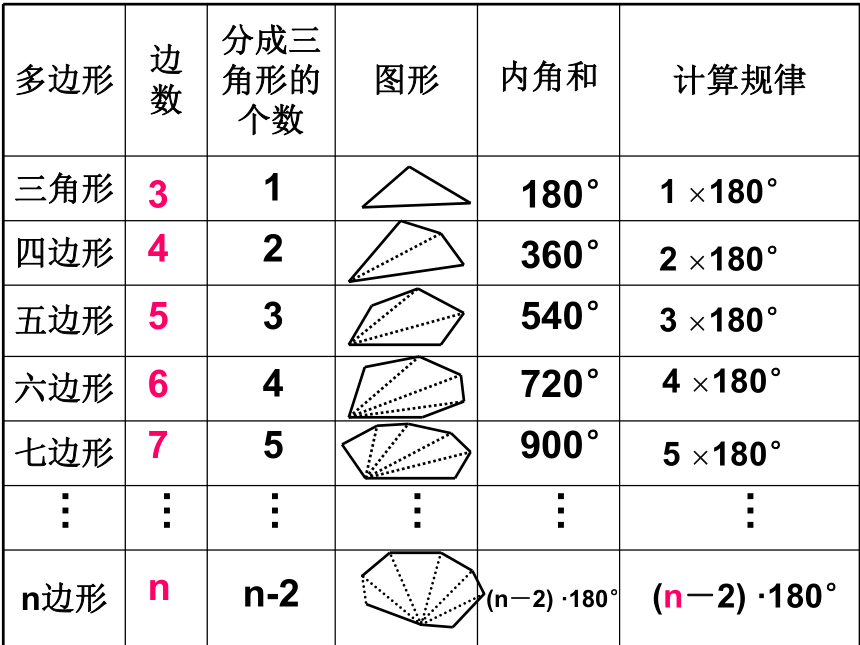
ABCDO方法2180°× 5 – 360°= 540°180°× 5=900°?五边形内角和540°??把一个五边形分成几个三角形,还有其他的分法吗?ABCDEF180° × 4 – 180° = 540°方法3怎样求多边形内角和的?………………34567n1n-22345180°360°540°720°900°(n-2) ·180°(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°结论:
1.n边形内角和(n-2)×180°(n≥3)
2.已知内角和求几边形:内角和÷180+24.n边形共有对角线 条(n≥3)3.n边形从一个顶点出发的对角线有(n-3)条
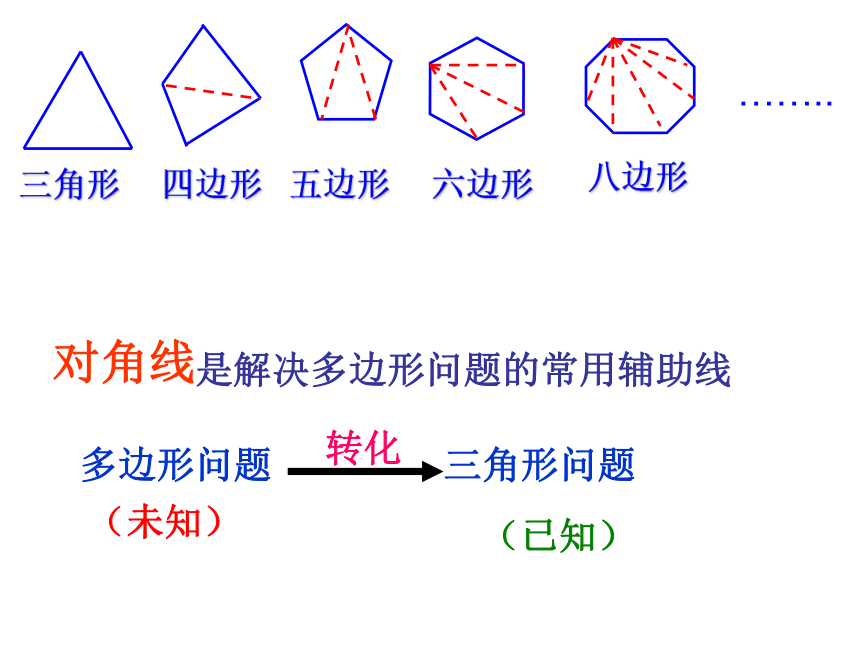
(n≥3)三角形六边形四边形八边形……..五边形是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化(未知)(已知)练一练: (2)已知一个多边形的内角和为720o ,则这个多边形是______边形6 (3)在五边形ABCDE中,若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______80o(1)求十边形的内角和的度数。 解:(10-2)×180°=8 ×180°=1440°答:十边形的内角和是1440°(4)过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
①这个多边形的边数.
② 这个多边形内角和的度数.5.填空(求边数)
(1)已知一个多边形的内角和为1080°,则它的边数为__。
(2)已知一个多边形的每一个内角都是156°,则它的边数为__。8156.正五边形 的每一个外角等于___.每一个内角等于_____,72°108°7.如果一个正多边形的一个内角等于120°,则这个多边 形的边 数是_____69.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____A.12 B.9 C. 8 D.78.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____A122.下列角度中,不能成为多边形内角和的是( )
A 540° B 280° C 1800° D 900°3.一个九边形的八个内角都是140°,那么,它的第九个内角为_______度. 1.多边形得边数增加一条时,其内角和就增加 度 能力训练: 5.随着多边形的边数n的增加,它的外角和( ) A.增加 B.减小 C.不变 D.不定 6.小明想设计一个内角和为2012°的多边形。他的想法会实现吗? .
4.五边形ABCDE中,若∠A = ∠D = 90°,
∠B:∠C :∠E = 3:8:7,求∠B,∠C ,∠E∵AB∥DE, CD∥AF(已知)∴∠1=∠3,∠2=∠4(两 直线平行,内错角相等) ∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F∴∠FAB+∠C+∠E= 1/2 ×720°=360°多边形的外角和www.yousee123.com外角:多边形的边与它的邻边的延长线组成的角。外角678910问题 大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
ABCDE12345(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。即:多边形的外角和等于360o3×180o-1×180o=360o4×180o-2×180o=360o5×180o-3×180o=360o6×180o-4×180o=360on×180o-(n-2)×180o=360o合作学习多边形的外角和从上表中得到了什么结论?结论:任何多边形的外角和为360°练习
(1)八边形的内角和为______,外角和为_____(2)已知一个多边形的每一个外角都是72o,求这个边形的边数为______例1:一个多边形的内角和等 于它的外 角和的3倍,它 是几边形?解:设它是n边形,则
(n-2).180=3×360
解得:n=8
答:它是8边形
www.czsx.com.cn例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。 解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°解:∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,∴∠CDE=∠FAB同理∠AFE=∠BCD,∠ABC=∠DEF∴∠FAB+∠BCD+∠DEF= ×720°=360°例3 一个六边形如图,已知AB∥DE,BC∥EF, CD∥AF,求∠A+∠C+∠E的度数。 (1)一个多边形的每一个外角都是600,这个多边形是几边形?它的内角和等于多少度?
(2)有没有这样的多边形,它的内角和是外角和的3倍? (3)一个多边形的每一个外角都相等,且每一个内角都比外角大900,求这个多边形的边数和每个内角的度数。 7、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,6、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,5、四边形的四个内角的比是8:6:3:7,求它的四个内角,4、一个多边形的内角和是外角和的4倍,这是几边形拓展:一个六边形如图,已知 BA∥DE ,∠B= ∠ E,∠C=∠F
(1)求证:CD∥AF
(2)求∠A+∠C+∠E的度数.强化训练 三角形三个内角的度数分别是(x+y)o, (x-y)o,xo,且x>y>0,则该三角形有一个内角为 ( )
A、30O B、45O C、60O D、90O
2.一个正多边形每一个内角都是120o,这个多边形是( ) A、正四边形 B、正五边形
C、正六边形 D、正七边形
CC 3.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为( )
A、13条 B、14条 C、15条 D、16条
下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
AD5.小明绕五边形各边走一圈,他共转了_ __度。
6.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是 ;360(1)、(2)、(4) 7.如下图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,则∠C=_ __∠BED= 。65°60°8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。内角和减少180O内角和不变内角和增加180O 把一个五边形切取一个角,将得到几边形?此时多边形的内角与外角有什么变化? 探究活动:如图, ∠A=45°, ∠B=25 ° ∠C=30 ° ,则 ∠D= 。EE100 °探究活动:如图, ∠A+∠B+∠C+∠E+∠F= 。G180 °探究活动:如图, ∠A+∠B+∠C+∠E+∠F= 。180 °巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。7×180O-2×360O=540O(4)求∠A+∠B+∠C+∠D+∠E+∠F的度数。 结论n边形的内角和为(n-2) ×180°(n≥3)n边形从一个顶点出发的对角线有(n-3)条(n≥3)n边形共有对角线 条(n≥3)任何多边形的外角和为360°再见SEE YOU !
你是怎样得到的?ABCD探究探究四边形的内角和2×180 o
=360 o4×180 o-360o
=360 o四边形的内角和是360o3×180 o-180o
=360 oEP B ACDE探究5边形内角和=3×180°=540°请你利用分割的方法探索五边形的内角是多少?方法1E
ABCDO方法2180°× 5 – 360°= 540°180°× 5=900°?五边形内角和540°??把一个五边形分成几个三角形,还有其他的分法吗?ABCDEF180° × 4 – 180° = 540°方法3怎样求多边形内角和的?………………34567n1n-22345180°360°540°720°900°(n-2) ·180°(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°结论:
1.n边形内角和(n-2)×180°(n≥3)
2.已知内角和求几边形:内角和÷180+24.n边形共有对角线 条(n≥3)3.n边形从一个顶点出发的对角线有(n-3)条
(n≥3)三角形六边形四边形八边形……..五边形是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化(未知)(已知)练一练: (2)已知一个多边形的内角和为720o ,则这个多边形是______边形6 (3)在五边形ABCDE中,若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______80o(1)求十边形的内角和的度数。 解:(10-2)×180°=8 ×180°=1440°答:十边形的内角和是1440°(4)过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
①这个多边形的边数.
② 这个多边形内角和的度数.5.填空(求边数)
(1)已知一个多边形的内角和为1080°,则它的边数为__。
(2)已知一个多边形的每一个内角都是156°,则它的边数为__。8156.正五边形 的每一个外角等于___.每一个内角等于_____,72°108°7.如果一个正多边形的一个内角等于120°,则这个多边 形的边 数是_____69.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____A.12 B.9 C. 8 D.78.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____A122.下列角度中,不能成为多边形内角和的是( )
A 540° B 280° C 1800° D 900°3.一个九边形的八个内角都是140°,那么,它的第九个内角为_______度. 1.多边形得边数增加一条时,其内角和就增加 度 能力训练: 5.随着多边形的边数n的增加,它的外角和( ) A.增加 B.减小 C.不变 D.不定 6.小明想设计一个内角和为2012°的多边形。他的想法会实现吗? .
4.五边形ABCDE中,若∠A = ∠D = 90°,
∠B:∠C :∠E = 3:8:7,求∠B,∠C ,∠E∵AB∥DE, CD∥AF(已知)∴∠1=∠3,∠2=∠4(两 直线平行,内错角相等) ∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F∴∠FAB+∠C+∠E= 1/2 ×720°=360°多边形的外角和www.yousee123.com外角:多边形的边与它的邻边的延长线组成的角。外角678910问题 大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?在图中标出它们.
ABCDE12345(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。即:多边形的外角和等于360o3×180o-1×180o=360o4×180o-2×180o=360o5×180o-3×180o=360o6×180o-4×180o=360on×180o-(n-2)×180o=360o合作学习多边形的外角和从上表中得到了什么结论?结论:任何多边形的外角和为360°练习
(1)八边形的内角和为______,外角和为_____(2)已知一个多边形的每一个外角都是72o,求这个边形的边数为______例1:一个多边形的内角和等 于它的外 角和的3倍,它 是几边形?解:设它是n边形,则
(n-2).180=3×360
解得:n=8
答:它是8边形
www.czsx.com.cn例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。 解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°解:∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,∴∠CDE=∠FAB同理∠AFE=∠BCD,∠ABC=∠DEF∴∠FAB+∠BCD+∠DEF= ×720°=360°例3 一个六边形如图,已知AB∥DE,BC∥EF, CD∥AF,求∠A+∠C+∠E的度数。 (1)一个多边形的每一个外角都是600,这个多边形是几边形?它的内角和等于多少度?
(2)有没有这样的多边形,它的内角和是外角和的3倍? (3)一个多边形的每一个外角都相等,且每一个内角都比外角大900,求这个多边形的边数和每个内角的度数。 7、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,6、一个多边形的每个内角都比相邻的外角3倍多20度,求这个多边形的边数,5、四边形的四个内角的比是8:6:3:7,求它的四个内角,4、一个多边形的内角和是外角和的4倍,这是几边形拓展:一个六边形如图,已知 BA∥DE ,∠B= ∠ E,∠C=∠F
(1)求证:CD∥AF
(2)求∠A+∠C+∠E的度数.强化训练 三角形三个内角的度数分别是(x+y)o, (x-y)o,xo,且x>y>0,则该三角形有一个内角为 ( )
A、30O B、45O C、60O D、90O
2.一个正多边形每一个内角都是120o,这个多边形是( ) A、正四边形 B、正五边形
C、正六边形 D、正七边形
CC 3.一个多边形木板,截去一个三角形后(截线不经过顶点),得到新多边形内角和为2160o,则原多边形的边数为( )
A、13条 B、14条 C、15条 D、16条
下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O; B、有一个外角是锐角的三角形是钝角三角形;C、三角形的外角中必有两个角是钝角; D、锐角三角形中两锐角的和必然小于60O;
AD5.小明绕五边形各边走一圈,他共转了_ __度。
6.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是 ;360(1)、(2)、(4) 7.如下图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,则∠C=_ __∠BED= 。65°60°8、两个多边形的边数比是1:2,两个多边形的内角和为1440度,求这两个多边形的边数,2、有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。内角和减少180O内角和不变内角和增加180O 把一个五边形切取一个角,将得到几边形?此时多边形的内角与外角有什么变化? 探究活动:如图, ∠A=45°, ∠B=25 ° ∠C=30 ° ,则 ∠D= 。EE100 °探究活动:如图, ∠A+∠B+∠C+∠E+∠F= 。G180 °探究活动:如图, ∠A+∠B+∠C+∠E+∠F= 。180 °巩固一下:
求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数。7×180O-2×360O=540O(4)求∠A+∠B+∠C+∠D+∠E+∠F的度数。 结论n边形的内角和为(n-2) ×180°(n≥3)n边形从一个顶点出发的对角线有(n-3)条(n≥3)n边形共有对角线 条(n≥3)任何多边形的外角和为360°再见SEE YOU !
