13.1.1等腰三角形的常用辅助线(共8张PPT)
文档属性
| 名称 | 13.1.1等腰三角形的常用辅助线(共8张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 537.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-13 08:52:44 | ||
图片预览

文档简介
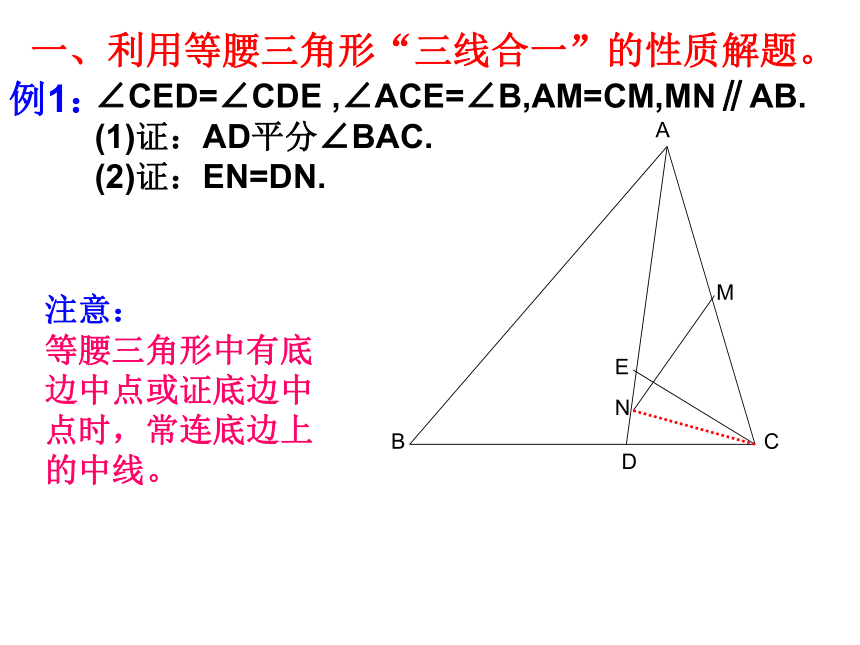
课件8张PPT。等腰三角形中的辅助线一、利用等腰三角形“三线合一”的性质解题。例1:∠CED=∠CDE ,∠ACE=∠B,AM=CM,MN∥AB.
(1)证:AD平分∠BAC.
(2)证:EN=DN.注意:
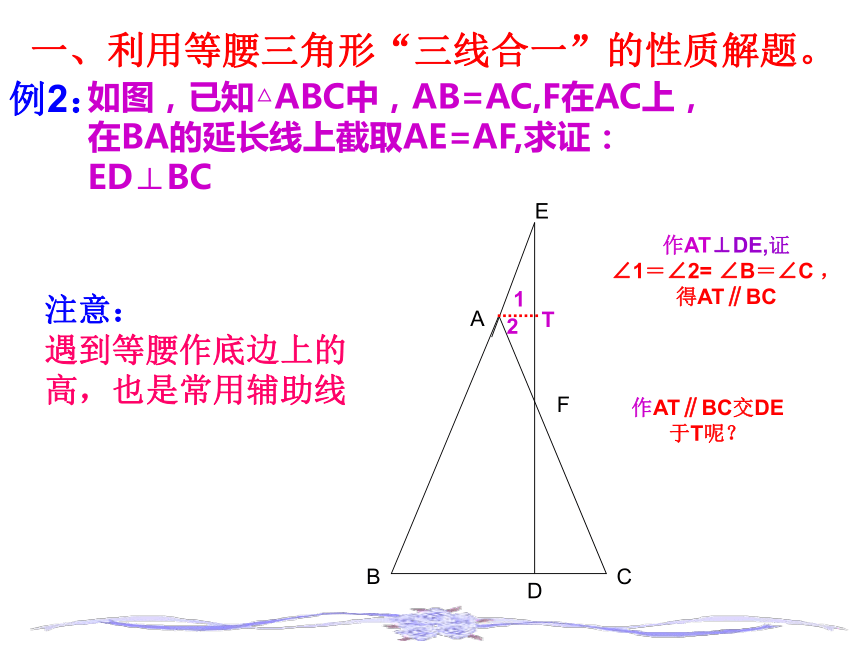
等腰三角形中有底边中点或证底边中点时,常连底边上的中线。 如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AE=AF,求证:ED⊥BCT作AT⊥DE,证
∠1=∠2= ∠B=∠C ,得AT∥BC12作AT∥BC交DE于T呢?一、利用等腰三角形“三线合一”的性质解题。例2:注意:
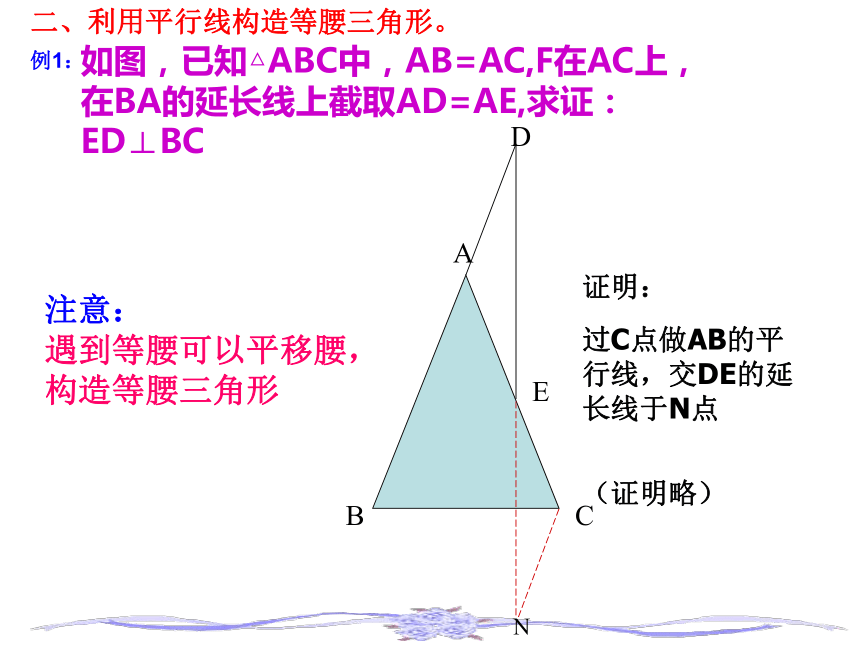
遇到等腰作底边上的高,也是常用辅助线 如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AD=AE,求证:ED⊥BC例1:二、利用平行线构造等腰三角形。证明:
过C点做AB的平行线,交DE的延长线于N点
(证明略)N注意:
遇到等腰可以平移腰,构造等腰三角形BACEDFT如图,AB=AC,CD=BE,求证:EF=DF二、利用平行线构造等腰三角形。例2:注意:
遇到等腰可以平移腰,构造等腰三角形二、利用平行线构造等腰三角形。例3:如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AD=AE,求证:ED⊥BC证明:
过D点做BC的平行线,交CA的延长线于O点,并延长DE交BC于F点
(证明略)注意:
遇到等腰可以平移底边,构造等腰三角形例、如图,在等腰直角三角形ABC中,∠ACB=90°,点D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF,
(1)求证:AD ⊥CF。
(2)若点G为AC的中点,连接GF,试确定GF与BC的关系,并说明理由。AFBDEC三、连接构造等腰三角形。G
(1)证:AD平分∠BAC.
(2)证:EN=DN.注意:
等腰三角形中有底边中点或证底边中点时,常连底边上的中线。 如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AE=AF,求证:ED⊥BCT作AT⊥DE,证
∠1=∠2= ∠B=∠C ,得AT∥BC12作AT∥BC交DE于T呢?一、利用等腰三角形“三线合一”的性质解题。例2:注意:
遇到等腰作底边上的高,也是常用辅助线 如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AD=AE,求证:ED⊥BC例1:二、利用平行线构造等腰三角形。证明:
过C点做AB的平行线,交DE的延长线于N点
(证明略)N注意:
遇到等腰可以平移腰,构造等腰三角形BACEDFT如图,AB=AC,CD=BE,求证:EF=DF二、利用平行线构造等腰三角形。例2:注意:
遇到等腰可以平移腰,构造等腰三角形二、利用平行线构造等腰三角形。例3:如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AD=AE,求证:ED⊥BC证明:
过D点做BC的平行线,交CA的延长线于O点,并延长DE交BC于F点
(证明略)注意:
遇到等腰可以平移底边,构造等腰三角形例、如图,在等腰直角三角形ABC中,∠ACB=90°,点D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF,
(1)求证:AD ⊥CF。
(2)若点G为AC的中点,连接GF,试确定GF与BC的关系,并说明理由。AFBDEC三、连接构造等腰三角形。G
