11.3用反比例函数解决问题同步强化练习(含解析)
文档属性
| 名称 | 11.3用反比例函数解决问题同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 22:00:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.3用反比例函数解决问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知矩形的面积为,则如图给出的四个图象中,能大致呈现矩形相邻边长与之间的函数关系的是( )
A. B. C. D.
2.当路程s一定时,速度v与时间t之间的函数关系是( )
A.正比例函数关系
B.反比例函数关系
C.一次函数关系
D.不成函数关系
3.已知经过闭合电路的电流(单位:)与电路的电阻(,单位:)是反比例函数关系.根据下表判断正确的为( )
20 30 40 50 60 70 80 90 100
5 … … … … … 1
A. B.当,
C.图象经过一、三象限 D.图象经过点
4.初三年级甲、乙、丙、丁四个级部举行了知识竞赛,如图,平面直角坐标系中,x轴表示级部参赛人数,y轴表示竞赛成绩的优秀率(该级部优秀人数与该级部参加竞赛人数的比值),其中描述甲、丁两个级部情况的点恰好在同一个反比例函数的图象上,则这四个级部在这次知识竞赛中成绩优秀人数的多少正确的是( )
A.甲乙丙丁 B.丙甲丁乙 C.甲丁乙丙 D.乙甲丁丙
5.固体糖溶于水可得到糖水.现有甲、乙、丙、丁四瓶糖水,如图,轴表示糖水质量,轴表示含糖浓度(瓶中糖固体质量与糖水质量的比值),其中乙、丁两点恰好在同一个反比例函数的图象上,则这四瓶糖水中含糖固体质量最多的是( )
A.甲 B.乙 C.丙 D.丁
6.甲、乙两地相距100km,汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(单位:h)与行驶速度 v(单位:km/h)之间的函数图像是( )
A. B.
C. D.
7.矩形面积是40 m2,设它的一边长为x(m),则矩形的另一边长y(m)与x的函数关系是( )
A.y=20-x B.y=40x C.y= D.y=
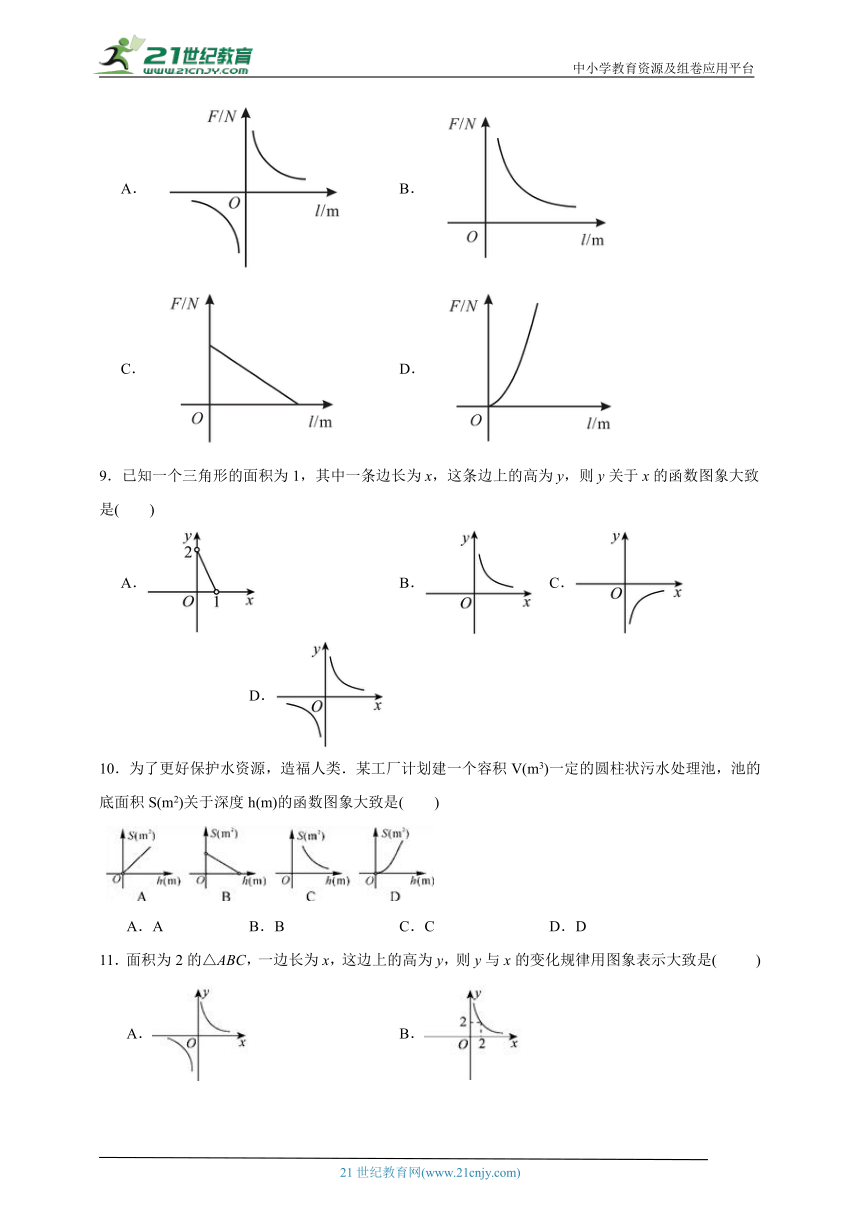
8.阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为和,则动力F关于动力臂l的函数图象为( )
A. B.
C. D.
9.已知一个三角形的面积为1,其中一条边长为x,这条边上的高为y,则y关于x的函数图象大致是( )
A. B. C. D.
10.为了更好保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的圆柱状污水处理池,池的底面积S(m2)关于深度h(m)的函数图象大致是( )
A.A B.B C.C D.D
11.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( )
A. B.
C. D.
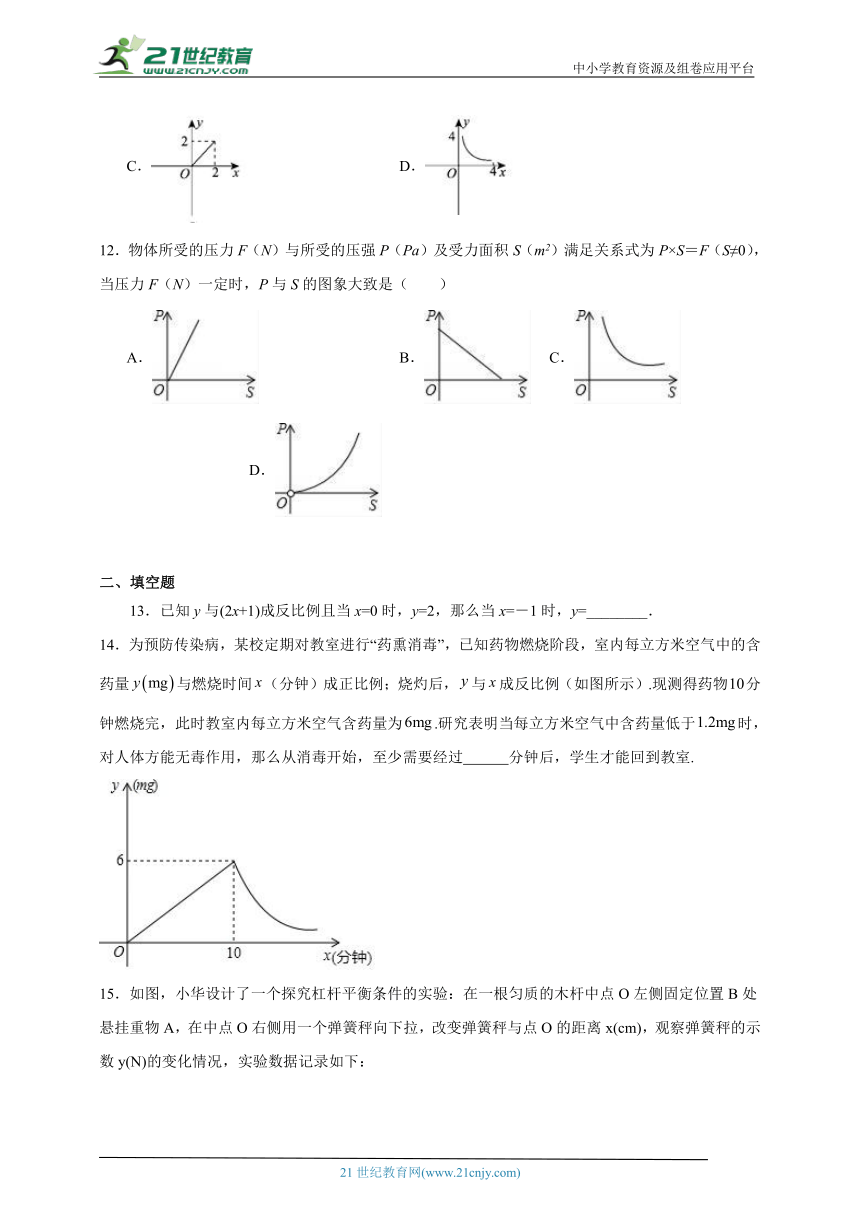
12.物体所受的压力F(N)与所受的压强P(Pa)及受力面积S(m2)满足关系式为P×S=F(S≠0),当压力F(N)一定时,P与S的图象大致是( )
A. B. C. D.
二、填空题
13.已知y与(2x+1)成反比例且当x=0时,y=2,那么当x=-1时,y=________.
14.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量与燃烧时间(分钟)成正比例;烧灼后,与成反比例(如图所示).现测得药物分钟燃烧完,此时教室内每立方米空气含药量为.研究表明当每立方米空气中含药量低于时,对人体方能无毒作用,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室.
15.如图,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况,实验数据记录如下:
则y与x之间的函数关系为 .
16.某蓄水池的排水管的平均排水量为每小时8立方米,6小时可以将满池水全部排空.现在排水量为平均每小时Q立方米,那么将满池水排空所需要的时间为t(小时),写出时间t(小时)与Q之间的函数表达式 .
17.小王驾车从甲地到乙地,他以70千米/时的平均速度4小时到达目的地,当他按原路匀速返回甲地时,汽车的速度y(千米/时)与时间x(时)(x≠0)的函数关系式为 .
三、解答题
18.某种型号热水器的容量为180升,设其工作时间为y分,每分的排水量为x升.
(1)写出y关于x的函数表达式和自变量x的取值范围;
(2)当每分钟的排水量为10升时,热水器工作多长时间?
(3)如果热水器可连续工作的时间不超过1小时,那么每分的排水量应控制在什么范围内?
19.某天上午7:30,小芳在家通过滴滴打车软件打车前往动车站搭乘当天上午8:30的动车.记汽车的行驶时间为t小时,行驶速度为v千米/小时(汽车行驶速度不超过60千米/小时).根据经验,v,t的一组对应值如下表:
V(千米/小时) 20 30 40 50 60
T(小时) 0.6 0.4 0.3 0.25 0.2
(1)根据表中的数据描点,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)若小芳从开始打车到上车用了10分钟,小芳想在动车出发前半小时到达动车站,若汽车的平均速度为32千米/小时,小芳能否在预定的时间内到达动车站?请说明理由;
(3)若汽车到达动车站的行驶时间t满足0.3<t<0.5,求平均速度v的取值范围.
20.学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边 y与另一边 x之间的函数关系式如下图所示.
(1)绿化带面积是多少 你能写出这一函数表达式吗
(2)完成下表,并回答问题:如果该绿化带的长不得超过40m,那么它的宽应控制在什么范围内
21.某商场出售一批进价为2元的贺卡,在市场营销中发现,此种贺卡的销售单价x(单位:元)与日销售量y(单位:张)之间有如下关系:
销售单价x(元) 3 4 5 6
日销售量y(张) 20 15 12 10
(1)根据表中数据在平面直角坐标系中描出实数对的对应点;
(2)确定y与x之间的函数关系式,并画出图象;
(3)设此种贺卡的日销售利润为w元,试求出w与x之间的函数关系式.若物价局规定此种贺卡的售价最高不超过10元/张,请你求出销售单价x定为多少元时,才能获得最大日销售利润?并求出最大日销售利润.
22.某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至元/度之间,经测算,若电价调至x元/度,则本年度新增的电量为y(亿度)与(元/度)成反比例关系,且当时,.
(1)求y与x之间的函数关系式;
(2)若每度电的成本价为0.3元,电价调至0.6元/度,请你预算本年度电力部门的纯收入.[纯收入用电量(实际电价成本价)]
23.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x(cm) … 10 15 20 25 30 …
y(N) … 30 20 15 12 10 …
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
24.某蓄水池的排水管每时排水8m3,6小时(h)可将满水池全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?
(3)写出t与Q之间的关系式
(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空?
《11.3用反比例函数解决问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B D C D C B B C
题号 11 12
答案 B C
1.A
【分析】根据矩形的面积公式得出xy=5,那么y与x之间的函数关系为反比例函数关系,再根据x、y所表示的实际意义得到x、y应大于0;即可得出答案.
【详解】∵矩形的面积为5,矩形相邻的两边长分别是y与x,
∴xy=5,
∴(x>0,y>0),
故选A.
【点睛】考查反比例函数的应用,解答该类题目的关键是确定两个变量之间的函数关系,利用实际意义确定所在的象限.
2.B
【详解】根据路程、速度、时间的关系;路程=速度×时间即可解题.
3.B
【分析】根据表格当电阻时,电流,设反比例函数为,由此求出电流与电路的电阻的关系,即可求解.
【详解】解:∵电流与电路的电阻是反比例函数关系,
∴设反比例函数解析式为,从表中可知电阻时,电流,
∴,
∴当时,;当时,,
∴,即选项错误;
当时,由得,
∴,即选项正确;
∵,
∴的图象在第一象限,即选项错误;
当时,,
∴图象不经过点,即选项错误.
故选:B.
【点睛】本题主要考查反比例函数图象的性质,掌握反比例函数的特点与实际情况中电阻与电流的关系是解题的关键.
4.D
【分析】根据题意可知的值即为该级部的优秀人数,再根据图象即可确定各级部人数的大小关系.
【详解】解:根据题意,可知的值即为该级部的优秀人数,
∵描述甲、丁两级部情况的点恰好在同一个反比例函数的图象上,
∴甲、丁两级部的优秀人数相同,
∵点乙在反比例函数图象上面,
∴乙级部的的值最大,即优秀人数最多,
∵点丙在反比例函数图象下面,
∴丙级部的的值最小,即优秀人数最少,
∴乙甲丁丙,
故选:D.
【点睛】本题考查了反比例函数的图象上点的坐标特征,结合实际含义理解图象上点的坐标含义是解题的关键.
5.C
【分析】本题考查反比例函数的实际应用,发现的值即为糖水中含糖固体质量成为解题的关键.
根据题意可知,的值即为糖水中含糖固体质量,再根据图象即可确定甲瓶糖水中含糖固体质量最少,丙瓶糖水中含糖固体质量最多,乙、丁两瓶糖水中含糖固体质量相同解题即可.
【详解】解:根据题意,可知的值即为糖水中含糖固体质量,
∵描述乙、丁两瓶情况的点恰好在同一个反比例函数的图象上,
∴乙、丁两瓶糖水中含糖固体质量相同,
∵点甲在反比例函数图象下面,点丙在反比例函数图象上面,
∴甲瓶的的值最小,即糖水中含糖固体质量最少,丙瓶的的值最大,即糖水中含糖固体质量最多.
故选∶C.
6.D
【分析】本题考查函数的图象.根据实际意义,写出函数的解析式,根据函数的类型,以及自变量的取值范围即可进行判断.
【详解】解:根据题意有:,
所以,
故与之间是反比例函数,其图象在第一象限.
故选:D.
7.C
【详解】试题解析:
由于矩形的另一边长=矩形面积÷一边长,
∴矩形的另一边长y(m)与x的函数关系是
故选C.
8.B
【分析】直接利用阻力×阻力臂=动力×动力臂,进而得出动力F关于动力臂l的函数关系式,从而确定其图象即可.
【详解】解:∵阻力×阻力臂=动力×动力臂,且阻力和阻力臂分别为和
∴动力F关于动力臂l的函数解析式为:,
即,是反比例函数,
又∵动力臂,
故B选项符合题意.
故选:B.
【点睛】本题考查了反比例函数的应用,正确读懂题意得出关系式是解本题的关键.
9.B
【分析】三角形的面积=×底边×底边上的高,那么底边=2三角形的面积÷这个底边上的高,线段应大于0,实际意义的函数都在第一象限.
【详解】∵xy=1,
∴y关于x的函数关系式为y=(x>0),由于线段的长不为0,故函数图象在第一象限.
故选:B.
【点睛】此题考查了反比例函数的应用,根据题意,找到所求量的等量关系是解决问题的关键.除法一般写成分式的形式,除号可看成分式线.
10.C
【详解】因为v=sh,所以,其中v是常量,h>0,所以函数图象是在第一象限的双曲线的一条分支,故选C.
11.B
【分析】由△ABC的面积及一边长为x,这边上的高为y可得关系式,即2=xy,y=(x>0).根据反比例函数y=的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限,因为x>0,所以其图象在第一象限,即可得出答案.
【详解】解:∵ xy=2
∴y= (x>0,y>0)
故选B.
【点睛】此题需要根据反比例函数的性质解答:反比例函数y=的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.
12.C
【分析】利用压强公式得到P=,则可判定P与S为反比例函数关系,然后利用S的取值范围可对各选项进行判断.
【详解】解:P=,
所以P与S为反比例函数关系,
因为S>0,
所以反比例函数图象在第一象限.
所以C选项是正确的.
【点睛】本题主要考查反比例函数的应用,解题关键在于确定两个变量之间的函数关系.
13.-2
【详解】试题解析:y与(2x+1)成反比例,
设
当x=0时,y=2,则 解得:
则:
当时,
故答案为-2.
14.50
【分析】先求得反比例函数的解析式,然后把代入反比例函数解析式,求出相应的即可;
【详解】解:设药物燃烧后与之间的解析式,把点代入得,解得,
关于的函数式为:;
当时,由;得,所以50分钟后学生才可进入教室;
故答案为50.
【点睛】本题考查了一次函数与反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
15.
【分析】通过表格我们可以得到表格中每组数据相乘为一个定值300,故我们可以猜想y与x之间是成反比例函数的关系,根据表格中的数据求出反比例函数的解析式,再将其余的点带入验证即可.
【详解】解:由表格猜想y与x之间的函数关系为反比例函数
解:设反比例函数解析式为
把x=10,y=30代入得:k=300
∴
将其余点带入均符合要求
∴y与x之间的函数关系式为:
故答案为:
【点睛】本题主要考查的是反比例函数的性质以及解析式的求法,正确的掌握反比例函数的性质是解题的关键.
16.t=
【分析】根据蓄水量=每小时排水量×排水时间,即可算出该蓄水池的蓄水总量,再由防水时间=蓄水总量÷每小时的排水量即可得出时间(小时)与之间的函数表达式.
【详解】某蓄水池的排水管的平均排水量为每小时立方米,小时可以将满池水全部排空,
该水池的蓄水量为(立方米),
,
.
故答案为:.
【点睛】本题考查了根据实际问题列出反比例函数关系式,解题的关键是根据数量关系列出关于的函数关系式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出函数关系式是关键.
17.y=(x>0)
【分析】根据速度×时间=路程,可以求出甲地去乙地的路程;再根据行驶速度=路程÷时间,得到y与x的函数解析式.
【详解】由已知得:甲地去乙地的路程=70×4=280,则
汽车的速度y(千米/时)与时间x(时)(x≠0)的函数关系式为y=(x>0).
故答案为y=(x>0).
【点睛】考查了根据实际问题列反比例函数关系式,清楚路程、速度、时间三者之间的关系对解答本题很重要.
18.(1)y=(x>0);(2)当x=10时,y==18(分);(3)当0<y≤60时,x≥3(升).
【分析】(1)工作时间为y(分)×每分钟的排水量为x(升)=总容量,所以可得出y与x的关系式.
(2)已知自变量求函数值;
(3)已知函数值求自变量.
【详解】解:(1)根据题意可知y=;
(2)在y=中,当x=10时,y==18,
∴热水器不间断工作的时间为18分;
(3)热水器可连续工作的最长时间为1小时,即0≤y≤60,
∴x≥3.∴每分的排水量x≥3.
【点睛】此题主要考查反比例函数在实际生活中的应用,根据题意准确的列式是解题的关键.
19.(1)v=;(2)若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;(3)平均速度v的取值范围是24<v<40
【分析】(1)根据表格中数据,可知v是t的反比例函数,设v=,利用待定系数法求出k即可;
(2)根据时间t=小时,求出速度,即可判断;
(3)根据自变量的取值范围,求出函数值的取值范围即可.
【详解】(1)根据表格中数据,可知v=,
∵v=20时,t=0.6,
∴k=20×0.6=12,
∴v= (t≥0.2).
(2)∵1﹣-=,
∴t=时,v==36>32,
∴若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;
(3)∵0.3<t<0.5,
∴24<v<40,
答:平均速度v的取值范围是24<v<40.
【点睛】本题考查反比例函数的应用,待定系数法等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于基础题.
20.(1)400(m 2),函数表达式为 y= ;(2)40,20, ,10,从图中可以看出.若长不超过40m,则它的宽应大于等于10m.
【详解】试题分析:
(1)由“矩形的长=面积÷宽”可得:,把点A(40,10)代入即可求出S和函数关系式;
(2)根据(1)中所得函数关系式即可计算出表格中与对应的的值,由计算结果即可得到所求结论;
试题解析:
(1)设矩形面积为S,由题意可得:,
把点A(40,10)代入可得:,
∴矩形的面积S=400,函数关系式为:;
(2)由计算完成表中数据如下:
(m) 10 20 30 40
(m) 40 20 10
由表中数据可知,若矩形长不超过40m,则矩形的宽不少于10m.
21.(1)见解析
(2)y与x之间的函数关系式为.画出图象见解析
(3)销售单价x定为10元时,才能获得最大日销售利润,最大日销售利润为 48元
【分析】(1)建立坐标系直接描点即可;
(2)要确定y与x之间的函数关系式,通过观察表中数据,可以发现y与x的乘积是相同的,都是60,所以可知y与x成反比例,用待定系数法求解后再验证即可;
(3)先确定与的函数关系式,然后根据售价最高不超过10元/张,利用函数的增减性即可得出答案.
【详解】(1)解:建立平面直角坐标系描点,如图所示:
(2)解:由题意设y与x之间的函数关系式为(且k为常数),把代入,得,
将,,分别代入,均成立,
所以y与x之间的函数关系式为,
画出的图象如上图所示;
(3)解:,
当时,w随x的增大而增大,
又因为,
所以当时,,
所以,销售单价x定为10元时,才能获得最大日销售利润,最大日销售利润为 48元.
【点睛】本题主要考查了反比例函数的定义,待定系数法以及利用反比例关系式求最大值的问题,解题的关键是知道两个变量的乘法是定值时是反比例关系.
22.(1)
(2)0.6亿元
【分析】此题主要考查了反比例函数的应用.
(1)利用本年度新增的电量为y(亿度)与(元)成反比例关系,假设出函数关系式求出即可;
(2)利用(1)中所求进而求出总用电量,进而得出纯收入.
【详解】(1)解:由题意,设.
当时,,
则,
解得,
故y与x之间的函数关系式为;
(2)解:由题意可得,,则,
故总用电量为亿度,
故本年度电力部门的纯收入为(亿元).
23.(1)图象见解析;;(2)随着弹簧秤与O点的距离不断减小,弹簧秤上的示数不断增大.
【分析】(1)在平面直角坐标系中描出相应的点,用平滑的曲线连接这些点,然后由图象猜测可y与x之间的函数关系为反比例函数关系;再根据待定系数法求解即可;
(2)把y=24代入(1)中的函数关系式即可求出弹簧秤与O点的距离,根据反比例函数的性质即可得出答案;
【详解】解:(1)取实验数据(10,30),(15,20),(20,15),(25,12),(30,10),并在平面直角坐标系中描出相应的点,用平滑的曲线连接这些点,得到如图所示的图象.由图象猜测y与x之间的函数关系为反比例函数关系.
设反比例函数为(k≠0),把 x=10,y=30代入,
得k=300,
∴,将各点代入均适合.
∴y与x之间的函数解析式为.
(2)把y=24代入,得x=12.5.
∴当弹簧秤的示数为24N时,弹簧秤与O点之间的距离是12.5cm.
随着弹簧秤与O点之间的距离不断减小,弹簧秤的示数不断增大.
【点睛】本题考查了反比例函数的应用,正确理解题意、得出相应的反比例函数关系式是解题的关键.
24.(1)48m3;(2)将减少;(3);(4)9.6m3;(5)4h
【分析】根据:每小时排水量×排水时间=蓄水池的容积,可以得到函数关系式.
(1)已知每小时排水量8m2及排水时间6h,可求蓄水池的容积为48m3;
(2)由基本等量关系得Q×t=48,判断函数关系,确定增减情况;
(3)由Q×t=48可得:t=;
(4)根据题意得出不等式,然后求解即可;
(5)把Q=12代入函数解析式求解即可.
【详解】(1)蓄水池的容积是:6×10=48m3;
(2)∵Q×t=48,Q与t成反比例关系.
∴Q增大,t将减少;
(3)t与Q之间的关系式为t=;
(4)∵t=≤5,解不等式得,Q≥9.6,即每小时的排水量至少为9.6m3;
(5)当Q=12时,由Q×t=48得t=4,即最少用4h可将满池水全部排空.
【点睛】本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式,再运用函数关系式解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
11.3用反比例函数解决问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知矩形的面积为,则如图给出的四个图象中,能大致呈现矩形相邻边长与之间的函数关系的是( )
A. B. C. D.
2.当路程s一定时,速度v与时间t之间的函数关系是( )
A.正比例函数关系
B.反比例函数关系
C.一次函数关系
D.不成函数关系
3.已知经过闭合电路的电流(单位:)与电路的电阻(,单位:)是反比例函数关系.根据下表判断正确的为( )
20 30 40 50 60 70 80 90 100
5 … … … … … 1
A. B.当,
C.图象经过一、三象限 D.图象经过点
4.初三年级甲、乙、丙、丁四个级部举行了知识竞赛,如图,平面直角坐标系中,x轴表示级部参赛人数,y轴表示竞赛成绩的优秀率(该级部优秀人数与该级部参加竞赛人数的比值),其中描述甲、丁两个级部情况的点恰好在同一个反比例函数的图象上,则这四个级部在这次知识竞赛中成绩优秀人数的多少正确的是( )
A.甲乙丙丁 B.丙甲丁乙 C.甲丁乙丙 D.乙甲丁丙
5.固体糖溶于水可得到糖水.现有甲、乙、丙、丁四瓶糖水,如图,轴表示糖水质量,轴表示含糖浓度(瓶中糖固体质量与糖水质量的比值),其中乙、丁两点恰好在同一个反比例函数的图象上,则这四瓶糖水中含糖固体质量最多的是( )
A.甲 B.乙 C.丙 D.丁
6.甲、乙两地相距100km,汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(单位:h)与行驶速度 v(单位:km/h)之间的函数图像是( )
A. B.
C. D.
7.矩形面积是40 m2,设它的一边长为x(m),则矩形的另一边长y(m)与x的函数关系是( )
A.y=20-x B.y=40x C.y= D.y=
8.阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为和,则动力F关于动力臂l的函数图象为( )
A. B.
C. D.
9.已知一个三角形的面积为1,其中一条边长为x,这条边上的高为y,则y关于x的函数图象大致是( )
A. B. C. D.
10.为了更好保护水资源,造福人类.某工厂计划建一个容积V(m3)一定的圆柱状污水处理池,池的底面积S(m2)关于深度h(m)的函数图象大致是( )
A.A B.B C.C D.D
11.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( )
A. B.
C. D.
12.物体所受的压力F(N)与所受的压强P(Pa)及受力面积S(m2)满足关系式为P×S=F(S≠0),当压力F(N)一定时,P与S的图象大致是( )
A. B. C. D.
二、填空题
13.已知y与(2x+1)成反比例且当x=0时,y=2,那么当x=-1时,y=________.
14.为预防传染病,某校定期对教室进行“药熏消毒”,已知药物燃烧阶段,室内每立方米空气中的含药量与燃烧时间(分钟)成正比例;烧灼后,与成反比例(如图所示).现测得药物分钟燃烧完,此时教室内每立方米空气含药量为.研究表明当每立方米空气中含药量低于时,对人体方能无毒作用,那么从消毒开始,至少需要经过 分钟后,学生才能回到教室.
15.如图,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况,实验数据记录如下:
则y与x之间的函数关系为 .
16.某蓄水池的排水管的平均排水量为每小时8立方米,6小时可以将满池水全部排空.现在排水量为平均每小时Q立方米,那么将满池水排空所需要的时间为t(小时),写出时间t(小时)与Q之间的函数表达式 .
17.小王驾车从甲地到乙地,他以70千米/时的平均速度4小时到达目的地,当他按原路匀速返回甲地时,汽车的速度y(千米/时)与时间x(时)(x≠0)的函数关系式为 .
三、解答题
18.某种型号热水器的容量为180升,设其工作时间为y分,每分的排水量为x升.
(1)写出y关于x的函数表达式和自变量x的取值范围;
(2)当每分钟的排水量为10升时,热水器工作多长时间?
(3)如果热水器可连续工作的时间不超过1小时,那么每分的排水量应控制在什么范围内?
19.某天上午7:30,小芳在家通过滴滴打车软件打车前往动车站搭乘当天上午8:30的动车.记汽车的行驶时间为t小时,行驶速度为v千米/小时(汽车行驶速度不超过60千米/小时).根据经验,v,t的一组对应值如下表:
V(千米/小时) 20 30 40 50 60
T(小时) 0.6 0.4 0.3 0.25 0.2
(1)根据表中的数据描点,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)若小芳从开始打车到上车用了10分钟,小芳想在动车出发前半小时到达动车站,若汽车的平均速度为32千米/小时,小芳能否在预定的时间内到达动车站?请说明理由;
(3)若汽车到达动车站的行驶时间t满足0.3<t<0.5,求平均速度v的取值范围.
20.学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边 y与另一边 x之间的函数关系式如下图所示.
(1)绿化带面积是多少 你能写出这一函数表达式吗
(2)完成下表,并回答问题:如果该绿化带的长不得超过40m,那么它的宽应控制在什么范围内
21.某商场出售一批进价为2元的贺卡,在市场营销中发现,此种贺卡的销售单价x(单位:元)与日销售量y(单位:张)之间有如下关系:
销售单价x(元) 3 4 5 6
日销售量y(张) 20 15 12 10
(1)根据表中数据在平面直角坐标系中描出实数对的对应点;
(2)确定y与x之间的函数关系式,并画出图象;
(3)设此种贺卡的日销售利润为w元,试求出w与x之间的函数关系式.若物价局规定此种贺卡的售价最高不超过10元/张,请你求出销售单价x定为多少元时,才能获得最大日销售利润?并求出最大日销售利润.
22.某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至元/度之间,经测算,若电价调至x元/度,则本年度新增的电量为y(亿度)与(元/度)成反比例关系,且当时,.
(1)求y与x之间的函数关系式;
(2)若每度电的成本价为0.3元,电价调至0.6元/度,请你预算本年度电力部门的纯收入.[纯收入用电量(实际电价成本价)]
23.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x(cm) … 10 15 20 25 30 …
y(N) … 30 20 15 12 10 …
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
24.某蓄水池的排水管每时排水8m3,6小时(h)可将满水池全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?
(3)写出t与Q之间的关系式
(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空?
《11.3用反比例函数解决问题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B D C D C B B C
题号 11 12
答案 B C
1.A
【分析】根据矩形的面积公式得出xy=5,那么y与x之间的函数关系为反比例函数关系,再根据x、y所表示的实际意义得到x、y应大于0;即可得出答案.
【详解】∵矩形的面积为5,矩形相邻的两边长分别是y与x,
∴xy=5,
∴(x>0,y>0),
故选A.
【点睛】考查反比例函数的应用,解答该类题目的关键是确定两个变量之间的函数关系,利用实际意义确定所在的象限.
2.B
【详解】根据路程、速度、时间的关系;路程=速度×时间即可解题.
3.B
【分析】根据表格当电阻时,电流,设反比例函数为,由此求出电流与电路的电阻的关系,即可求解.
【详解】解:∵电流与电路的电阻是反比例函数关系,
∴设反比例函数解析式为,从表中可知电阻时,电流,
∴,
∴当时,;当时,,
∴,即选项错误;
当时,由得,
∴,即选项正确;
∵,
∴的图象在第一象限,即选项错误;
当时,,
∴图象不经过点,即选项错误.
故选:B.
【点睛】本题主要考查反比例函数图象的性质,掌握反比例函数的特点与实际情况中电阻与电流的关系是解题的关键.
4.D
【分析】根据题意可知的值即为该级部的优秀人数,再根据图象即可确定各级部人数的大小关系.
【详解】解:根据题意,可知的值即为该级部的优秀人数,
∵描述甲、丁两级部情况的点恰好在同一个反比例函数的图象上,
∴甲、丁两级部的优秀人数相同,
∵点乙在反比例函数图象上面,
∴乙级部的的值最大,即优秀人数最多,
∵点丙在反比例函数图象下面,
∴丙级部的的值最小,即优秀人数最少,
∴乙甲丁丙,
故选:D.
【点睛】本题考查了反比例函数的图象上点的坐标特征,结合实际含义理解图象上点的坐标含义是解题的关键.
5.C
【分析】本题考查反比例函数的实际应用,发现的值即为糖水中含糖固体质量成为解题的关键.
根据题意可知,的值即为糖水中含糖固体质量,再根据图象即可确定甲瓶糖水中含糖固体质量最少,丙瓶糖水中含糖固体质量最多,乙、丁两瓶糖水中含糖固体质量相同解题即可.
【详解】解:根据题意,可知的值即为糖水中含糖固体质量,
∵描述乙、丁两瓶情况的点恰好在同一个反比例函数的图象上,
∴乙、丁两瓶糖水中含糖固体质量相同,
∵点甲在反比例函数图象下面,点丙在反比例函数图象上面,
∴甲瓶的的值最小,即糖水中含糖固体质量最少,丙瓶的的值最大,即糖水中含糖固体质量最多.
故选∶C.
6.D
【分析】本题考查函数的图象.根据实际意义,写出函数的解析式,根据函数的类型,以及自变量的取值范围即可进行判断.
【详解】解:根据题意有:,
所以,
故与之间是反比例函数,其图象在第一象限.
故选:D.
7.C
【详解】试题解析:
由于矩形的另一边长=矩形面积÷一边长,
∴矩形的另一边长y(m)与x的函数关系是
故选C.
8.B
【分析】直接利用阻力×阻力臂=动力×动力臂,进而得出动力F关于动力臂l的函数关系式,从而确定其图象即可.
【详解】解:∵阻力×阻力臂=动力×动力臂,且阻力和阻力臂分别为和
∴动力F关于动力臂l的函数解析式为:,
即,是反比例函数,
又∵动力臂,
故B选项符合题意.
故选:B.
【点睛】本题考查了反比例函数的应用,正确读懂题意得出关系式是解本题的关键.
9.B
【分析】三角形的面积=×底边×底边上的高,那么底边=2三角形的面积÷这个底边上的高,线段应大于0,实际意义的函数都在第一象限.
【详解】∵xy=1,
∴y关于x的函数关系式为y=(x>0),由于线段的长不为0,故函数图象在第一象限.
故选:B.
【点睛】此题考查了反比例函数的应用,根据题意,找到所求量的等量关系是解决问题的关键.除法一般写成分式的形式,除号可看成分式线.
10.C
【详解】因为v=sh,所以,其中v是常量,h>0,所以函数图象是在第一象限的双曲线的一条分支,故选C.
11.B
【分析】由△ABC的面积及一边长为x,这边上的高为y可得关系式,即2=xy,y=(x>0).根据反比例函数y=的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限,因为x>0,所以其图象在第一象限,即可得出答案.
【详解】解:∵ xy=2
∴y= (x>0,y>0)
故选B.
【点睛】此题需要根据反比例函数的性质解答:反比例函数y=的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.
12.C
【分析】利用压强公式得到P=,则可判定P与S为反比例函数关系,然后利用S的取值范围可对各选项进行判断.
【详解】解:P=,
所以P与S为反比例函数关系,
因为S>0,
所以反比例函数图象在第一象限.
所以C选项是正确的.
【点睛】本题主要考查反比例函数的应用,解题关键在于确定两个变量之间的函数关系.
13.-2
【详解】试题解析:y与(2x+1)成反比例,
设
当x=0时,y=2,则 解得:
则:
当时,
故答案为-2.
14.50
【分析】先求得反比例函数的解析式,然后把代入反比例函数解析式,求出相应的即可;
【详解】解:设药物燃烧后与之间的解析式,把点代入得,解得,
关于的函数式为:;
当时,由;得,所以50分钟后学生才可进入教室;
故答案为50.
【点睛】本题考查了一次函数与反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
15.
【分析】通过表格我们可以得到表格中每组数据相乘为一个定值300,故我们可以猜想y与x之间是成反比例函数的关系,根据表格中的数据求出反比例函数的解析式,再将其余的点带入验证即可.
【详解】解:由表格猜想y与x之间的函数关系为反比例函数
解:设反比例函数解析式为
把x=10,y=30代入得:k=300
∴
将其余点带入均符合要求
∴y与x之间的函数关系式为:
故答案为:
【点睛】本题主要考查的是反比例函数的性质以及解析式的求法,正确的掌握反比例函数的性质是解题的关键.
16.t=
【分析】根据蓄水量=每小时排水量×排水时间,即可算出该蓄水池的蓄水总量,再由防水时间=蓄水总量÷每小时的排水量即可得出时间(小时)与之间的函数表达式.
【详解】某蓄水池的排水管的平均排水量为每小时立方米,小时可以将满池水全部排空,
该水池的蓄水量为(立方米),
,
.
故答案为:.
【点睛】本题考查了根据实际问题列出反比例函数关系式,解题的关键是根据数量关系列出关于的函数关系式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出函数关系式是关键.
17.y=(x>0)
【分析】根据速度×时间=路程,可以求出甲地去乙地的路程;再根据行驶速度=路程÷时间,得到y与x的函数解析式.
【详解】由已知得:甲地去乙地的路程=70×4=280,则
汽车的速度y(千米/时)与时间x(时)(x≠0)的函数关系式为y=(x>0).
故答案为y=(x>0).
【点睛】考查了根据实际问题列反比例函数关系式,清楚路程、速度、时间三者之间的关系对解答本题很重要.
18.(1)y=(x>0);(2)当x=10时,y==18(分);(3)当0<y≤60时,x≥3(升).
【分析】(1)工作时间为y(分)×每分钟的排水量为x(升)=总容量,所以可得出y与x的关系式.
(2)已知自变量求函数值;
(3)已知函数值求自变量.
【详解】解:(1)根据题意可知y=;
(2)在y=中,当x=10时,y==18,
∴热水器不间断工作的时间为18分;
(3)热水器可连续工作的最长时间为1小时,即0≤y≤60,
∴x≥3.∴每分的排水量x≥3.
【点睛】此题主要考查反比例函数在实际生活中的应用,根据题意准确的列式是解题的关键.
19.(1)v=;(2)若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;(3)平均速度v的取值范围是24<v<40
【分析】(1)根据表格中数据,可知v是t的反比例函数,设v=,利用待定系数法求出k即可;
(2)根据时间t=小时,求出速度,即可判断;
(3)根据自变量的取值范围,求出函数值的取值范围即可.
【详解】(1)根据表格中数据,可知v=,
∵v=20时,t=0.6,
∴k=20×0.6=12,
∴v= (t≥0.2).
(2)∵1﹣-=,
∴t=时,v==36>32,
∴若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;
(3)∵0.3<t<0.5,
∴24<v<40,
答:平均速度v的取值范围是24<v<40.
【点睛】本题考查反比例函数的应用,待定系数法等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于基础题.
20.(1)400(m 2),函数表达式为 y= ;(2)40,20, ,10,从图中可以看出.若长不超过40m,则它的宽应大于等于10m.
【详解】试题分析:
(1)由“矩形的长=面积÷宽”可得:,把点A(40,10)代入即可求出S和函数关系式;
(2)根据(1)中所得函数关系式即可计算出表格中与对应的的值,由计算结果即可得到所求结论;
试题解析:
(1)设矩形面积为S,由题意可得:,
把点A(40,10)代入可得:,
∴矩形的面积S=400,函数关系式为:;
(2)由计算完成表中数据如下:
(m) 10 20 30 40
(m) 40 20 10
由表中数据可知,若矩形长不超过40m,则矩形的宽不少于10m.
21.(1)见解析
(2)y与x之间的函数关系式为.画出图象见解析
(3)销售单价x定为10元时,才能获得最大日销售利润,最大日销售利润为 48元
【分析】(1)建立坐标系直接描点即可;
(2)要确定y与x之间的函数关系式,通过观察表中数据,可以发现y与x的乘积是相同的,都是60,所以可知y与x成反比例,用待定系数法求解后再验证即可;
(3)先确定与的函数关系式,然后根据售价最高不超过10元/张,利用函数的增减性即可得出答案.
【详解】(1)解:建立平面直角坐标系描点,如图所示:
(2)解:由题意设y与x之间的函数关系式为(且k为常数),把代入,得,
将,,分别代入,均成立,
所以y与x之间的函数关系式为,
画出的图象如上图所示;
(3)解:,
当时,w随x的增大而增大,
又因为,
所以当时,,
所以,销售单价x定为10元时,才能获得最大日销售利润,最大日销售利润为 48元.
【点睛】本题主要考查了反比例函数的定义,待定系数法以及利用反比例关系式求最大值的问题,解题的关键是知道两个变量的乘法是定值时是反比例关系.
22.(1)
(2)0.6亿元
【分析】此题主要考查了反比例函数的应用.
(1)利用本年度新增的电量为y(亿度)与(元)成反比例关系,假设出函数关系式求出即可;
(2)利用(1)中所求进而求出总用电量,进而得出纯收入.
【详解】(1)解:由题意,设.
当时,,
则,
解得,
故y与x之间的函数关系式为;
(2)解:由题意可得,,则,
故总用电量为亿度,
故本年度电力部门的纯收入为(亿元).
23.(1)图象见解析;;(2)随着弹簧秤与O点的距离不断减小,弹簧秤上的示数不断增大.
【分析】(1)在平面直角坐标系中描出相应的点,用平滑的曲线连接这些点,然后由图象猜测可y与x之间的函数关系为反比例函数关系;再根据待定系数法求解即可;
(2)把y=24代入(1)中的函数关系式即可求出弹簧秤与O点的距离,根据反比例函数的性质即可得出答案;
【详解】解:(1)取实验数据(10,30),(15,20),(20,15),(25,12),(30,10),并在平面直角坐标系中描出相应的点,用平滑的曲线连接这些点,得到如图所示的图象.由图象猜测y与x之间的函数关系为反比例函数关系.
设反比例函数为(k≠0),把 x=10,y=30代入,
得k=300,
∴,将各点代入均适合.
∴y与x之间的函数解析式为.
(2)把y=24代入,得x=12.5.
∴当弹簧秤的示数为24N时,弹簧秤与O点之间的距离是12.5cm.
随着弹簧秤与O点之间的距离不断减小,弹簧秤的示数不断增大.
【点睛】本题考查了反比例函数的应用,正确理解题意、得出相应的反比例函数关系式是解题的关键.
24.(1)48m3;(2)将减少;(3);(4)9.6m3;(5)4h
【分析】根据:每小时排水量×排水时间=蓄水池的容积,可以得到函数关系式.
(1)已知每小时排水量8m2及排水时间6h,可求蓄水池的容积为48m3;
(2)由基本等量关系得Q×t=48,判断函数关系,确定增减情况;
(3)由Q×t=48可得:t=;
(4)根据题意得出不等式,然后求解即可;
(5)把Q=12代入函数解析式求解即可.
【详解】(1)蓄水池的容积是:6×10=48m3;
(2)∵Q×t=48,Q与t成反比例关系.
∴Q增大,t将减少;
(3)t与Q之间的关系式为t=;
(4)∵t=≤5,解不等式得,Q≥9.6,即每小时的排水量至少为9.6m3;
(5)当Q=12时,由Q×t=48得t=4,即最少用4h可将满池水全部排空.
【点睛】本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式,再运用函数关系式解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
