人教版初中数学七上 课件3.4实际问题与一元一次方程(共19张PPT)
文档属性
| 名称 | 人教版初中数学七上 课件3.4实际问题与一元一次方程(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-13 10:14:42 | ||
图片预览






文档简介
课件19张PPT。3.4实际问题与一元一次方程潘塘街初级中学 罗锦海列方程解应用问题大致包含哪些步骤?1. 审:审题,分析题目中的数量关系;2. 设:设适当的未知数,并表示未知量;3. 列:根据题目中的数量关系列方程;4. 解:解这个方程求未知数的值;5. 答:检验并写出答案.复习与回顾学习目标工程问题中的量及其关系:1.工作效率:2.工程问题中的量及其关系:3.总工作量可看做“ ”单位时间内完成的工作量工作量=工作效率×工作时间1各部分工作量之和=总工作总量知识回顾:工程问题中的等量关系:工作总量 = 工作效率×工作时间 一件工作,甲单独做x小时完成,乙单
独做y小时完成,那么甲、乙的工作效率分
别为??? ????、???? ???;甲、乙合作m天可以完成
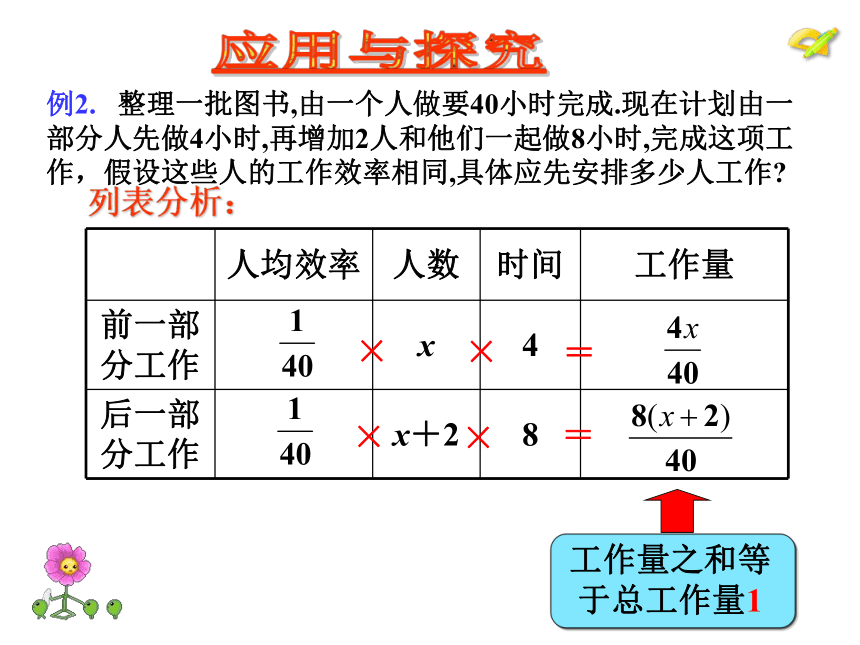
的工作量为??? ? 或 ???。 填空:思考:例2. 整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?工程问题列表分析:例2. 整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?应用与探究 解:设安排 x 人先做4 h.
依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.1.审题找等量关系在草纸上进行,书面格式中主要写
“设”、“列” 、“解”、“答”四个步骤的解题过程。
2.列方程时,要注意方程两边应是同一类量,并且单位要统一。
3.解应用题,切勿漏写“答”,“设”和“答”都必须写清
单位名称。
4.一般情况下,题中所给条件在列方程时不能重复使用,也不能
漏掉不用,重复使用某一个条件,会得到一个恒等式,无法
求得应用题的解。
5.对于求得的解,还要看它是否符合实际意义,再写“答”
列方程解应用题的注意事项: 一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线? 解:设 x天可以铺好这条管线.
依题意得: ,
解方程,得: x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.勇敢闯关 一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果甲工程队先施工3天,剩下的由甲乙合作,还需多少天可以铺好这条管线? 解:设还需 x天可以铺好这条管线.
依题意得:
勇敢闯关 一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果甲乙工程队合作施工2天,因甲工程队另有任务,剩下的由乙工程队完成,乙还需多少天可以铺好这条管线? 解:设乙还需x天可以铺好这条管线.
依题意得:
勇敢闯关 1、 一件工作,甲单独做需50天才能完成,乙独做需要45天完成。问在乙单独做7天以后,甲、乙合作多少天可以完成。解:设甲、乙合作x天可以完成,依题意,得:解得: x = 20答:甲、乙合作20天可以完成。快乐达标巩固练习2、某管道由甲、乙两工程队单独施工分别需要30
天、20天。
(1)如果两队从两端同时相向施工,需要多少
天铺好?
(2)又知甲队单独施工每天需付200元的施工
费,乙队单独施工每天需付280元施工费,
那么是由甲队单独施工,还是乙队单独施
工,还是两队同时施工,请你按照少花钱
多办事的原则,设计一个方案,并说明理
由。 巩固练习解:(1)设需要 x 天铺好,依题意,得:解得: x = 12∴ 需要12天铺好。(2)若单独由甲队施工,则需30天完成,花费
200×30=6000(元);若单独由乙队施工,则需20天完成,花费
280×20=5600(元);若由甲、乙队共同施工,则需12天完成,
花费200×12+280×12=5760(元)。∴ 按照少花钱多办事的原则,应选择由乙
队单独施工完成。谈谈你的收获和困惑 课后作业:必做题:教材练习106页4题5题预习作业:预习“销售中的营销” “球赛积分表问题”。三、小结与归纳 问题5:用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么? ? 解题后的反思 议 一 议(1)用方程解实际问题的基本过程:审(借助表格,图表等提炼数学信息,理解问题中的基本数学关系);
设(用代数式表示实际问题中的文字语言,文字语言符号化);
列(找到所列代数式中的基本等量关系,列出方程);
解(解方程);
验(是否是方程的解,实际问题有意义);
答(实际问题的答案).
独做y小时完成,那么甲、乙的工作效率分
别为??? ????、???? ???;甲、乙合作m天可以完成
的工作量为??? ? 或 ???。 填空:思考:例2. 整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?工程问题列表分析:例2. 整理一批图书,由一个人做要40小时完成.现在计划由一部分人先做4小时,再增加2人和他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?应用与探究 解:设安排 x 人先做4 h.
依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.1.审题找等量关系在草纸上进行,书面格式中主要写
“设”、“列” 、“解”、“答”四个步骤的解题过程。
2.列方程时,要注意方程两边应是同一类量,并且单位要统一。
3.解应用题,切勿漏写“答”,“设”和“答”都必须写清
单位名称。
4.一般情况下,题中所给条件在列方程时不能重复使用,也不能
漏掉不用,重复使用某一个条件,会得到一个恒等式,无法
求得应用题的解。
5.对于求得的解,还要看它是否符合实际意义,再写“答”
列方程解应用题的注意事项: 一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线? 解:设 x天可以铺好这条管线.
依题意得: ,
解方程,得: x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.勇敢闯关 一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果甲工程队先施工3天,剩下的由甲乙合作,还需多少天可以铺好这条管线? 解:设还需 x天可以铺好这条管线.
依题意得:
勇敢闯关 一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果甲乙工程队合作施工2天,因甲工程队另有任务,剩下的由乙工程队完成,乙还需多少天可以铺好这条管线? 解:设乙还需x天可以铺好这条管线.
依题意得:
勇敢闯关 1、 一件工作,甲单独做需50天才能完成,乙独做需要45天完成。问在乙单独做7天以后,甲、乙合作多少天可以完成。解:设甲、乙合作x天可以完成,依题意,得:解得: x = 20答:甲、乙合作20天可以完成。快乐达标巩固练习2、某管道由甲、乙两工程队单独施工分别需要30
天、20天。
(1)如果两队从两端同时相向施工,需要多少
天铺好?
(2)又知甲队单独施工每天需付200元的施工
费,乙队单独施工每天需付280元施工费,
那么是由甲队单独施工,还是乙队单独施
工,还是两队同时施工,请你按照少花钱
多办事的原则,设计一个方案,并说明理
由。 巩固练习解:(1)设需要 x 天铺好,依题意,得:解得: x = 12∴ 需要12天铺好。(2)若单独由甲队施工,则需30天完成,花费
200×30=6000(元);若单独由乙队施工,则需20天完成,花费
280×20=5600(元);若由甲、乙队共同施工,则需12天完成,
花费200×12+280×12=5760(元)。∴ 按照少花钱多办事的原则,应选择由乙
队单独施工完成。谈谈你的收获和困惑 课后作业:必做题:教材练习106页4题5题预习作业:预习“销售中的营销” “球赛积分表问题”。三、小结与归纳 问题5:用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么? ? 解题后的反思 议 一 议(1)用方程解实际问题的基本过程:审(借助表格,图表等提炼数学信息,理解问题中的基本数学关系);
设(用代数式表示实际问题中的文字语言,文字语言符号化);
列(找到所列代数式中的基本等量关系,列出方程);
解(解方程);
验(是否是方程的解,实际问题有意义);
答(实际问题的答案).
