14.3 实 数 导学练课件(共48张PPT) 2025-2025学年冀教版八年级数学上册
文档属性
| 名称 | 14.3 实 数 导学练课件(共48张PPT) 2025-2025学年冀教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 20:44:50 | ||
图片预览










文档简介
(共48张PPT)
14.3 实 数
第十四章 实 数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
无理数
实数的概念及分类
实数与数轴
实数的性质
实数的大小比较
确定一个无理数的大致范围
知1-讲
感悟新知
知识点
无理数
1
1. 定义
无限不循环小数叫做无理数 .
判断标准: 小数位数无限,小数形式为不循环 .
感悟新知
知1-讲
特别警示
1. 无理数都是无限小数,但无限小数不一定是无理数,只有无限不循环小数才是无理数.例如: 0. 是无限小数,但不是无理数.
2. 某些数的平方根或立方根是无理数,但带根号的数不一定都是无理数 .例如 , 就不是无理数.
感悟新知
2. 三种常见形式
(1)开方开不尽而得到的数,如 , ,…;
(2)含有 π 的一类数,如 π, π, π +1,…;
(3) 以无限不循环小数的形式出现的具有特定结构的数,如0.101 001 000 1…(每相邻两个 1 之间依次多一个 0) .
知1-讲
感悟新知
3. 无理数与有理数的区别
(1) 有理数是有限小数或无限循环小数,而无理数是无限不循环小数;
(2) 所有的有理数都可以写成分数的形式(整数可以看成分母为 1 的分数),而无理数不能写成分数的形式 .
知1-讲
知1-练
感悟新知
考向:利用无理数的定义识别无理数
[母题 教材 P81 练习 T2 ]下列各数:3.141 59, - 3,0.131 131 113…(每相邻两个 3 之间依次多一个 1),
π - 5, +1, - 中,无理数有_______个 .
例1
3
解题秘方:根据无理数的三种常见形式去辨析.
知1-练
感悟新知
解:∵ 3.141 59 是有限小数, ∴ 3.141 59 是有理数 .
∵ - 3= - 2, ∴ - 3是有理数 .
∵ 0.131 131 113…(每相邻两个 3 之间依次多一个 1)是无限不循环小数, ∴ 0.131 131 113…(每相邻两个 3 之间依次多一个 1)是无理数 .
∵ π 是无理数, ∴ π - 5 是无理数 .
∵ 是无理数, ∴ +1 是无理数 .
∵ - 是分数, ∴ - 是有理数 .
知1-练
感悟新知
1-1. [ 中考·长沙 ] 下列各数中,是无理数的是( )
A. B.π
C. -1 D. 0
B
变式训练
知1-练
感悟新知
1-2.在 , 3, ,0.124, 3.141 592 6, 中,无理数有 ________个 .
2
感悟新知
知2-讲
知识点
实数的概念及分类
2
1. 定义 有理数和无理数统称为实数 .
特别解读:在实数范围内,一个数不是有理数,那么它就一定是无理数,反之亦成立.
知2-讲
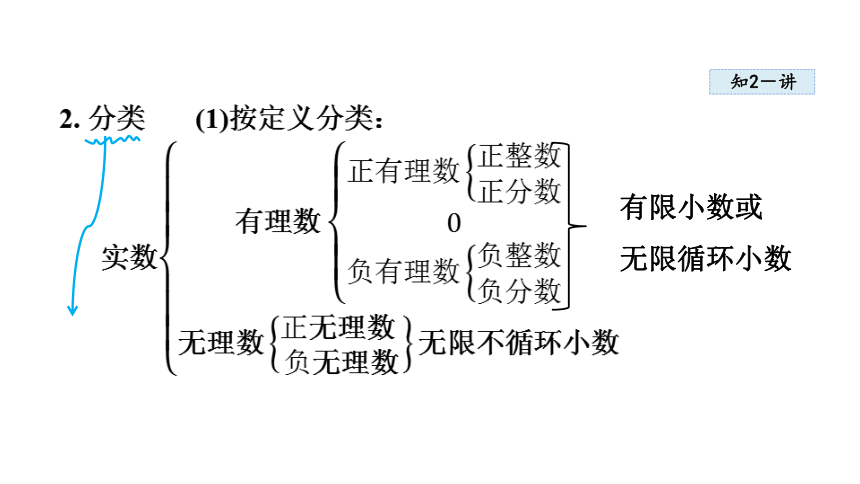
2. 分类 (1)按定义分类:
实数
有限小数或
无限循环小数
感悟新知
知2-讲
感悟新知
特别提醒
1. 实数的分类有不同的方法,但不论用哪一种分类方法,都要按同一标准,做到不重复不遗漏;
2. 对实数进行分类时, 某些数应先进行计算或化简,然后根据最后的结果进行分类. 不能看到带根号的数,就认为是无理数,也不能看到有分数线的数,就认为是有理数.
感悟新知
知2-讲
实数
0 既不是正实数也不是负实数.
(2) 按性质分类:
知2-练
[母题 教材P84 练习T1] 把下列各数填入相应的大括号内:
-,-,,,- 3,0,-π,-,
-4.201,3.101 001 000 1…(每相邻两个1之间0的个数逐次加1).
有理数:{ …};无理数:{ …};
整数:{ …};分数:{ …};
正实数:{ …};负实数:{ …}.
. .
例2
考向:利用实数中各类数的特征进行分类
知2-练
解题秘方:根据有理数、无理数等概念进行分类时,应注意先把一些数进行化简再判断.
知2-练
解:有理数:{-,,- 3,0, -,
-4. 0,…}.
无理数:{-,,-π,3.101 001 000 1… (每相邻两个1 之间0的个数逐次加1),…}.
判断时要看结果,不要看表面形式,如 - 3 =2是有理数,而不是无理数.
知2-练
整数:{- 3,0, …}.
分数:{-,,-,-4.0,…}.
正实数:{, ,- 3,3.101 001 000 1… (每相邻两个1 之间0的个数逐次加1),…}.
负实数:{-,-,-π,-,-4. 0,…}.
知2-练
. .
. .
2-1. 把下列各数分别填到相应的横线上:
-3.141 519 26,,3 ,,,0.21,0,-3,0.202 002 000 200 002…(每相邻两个2之间0的个数逐次加1).
(1)正有理数:_________________ ;
(2)负无理数: __________________;
(3)负实数: ______________________.
变式训练
知2-练
感悟新知
2-2.在 , - ,3. , - 8, 3, - ,0, -π 中,有理数有 m个,整数有 p 个,分数有 k 个,负数有 t 个,则 m-k+t+p= _________.
9
知3-讲
知识点
实数与数轴
3
实数与数轴间的关系
实数与数轴上的点是一一对应的.
“一一对应”包含着两层含义:
①每一个实数都可以用数轴上的一个点来表示;
②数轴上的每一个点都表示一个实数.
知3-讲
感悟新知
特别解读
借助数轴上的点可以把实数直观地表示出来,数轴上的任意一点表示的数,不是有理数就是无理数.
知3-练
感悟新知
下列说法正确的有( )
①数轴上的任意一点都表示一个有理数;
②每个无理数都可以用数轴上的一个点来表示;
③任意一个实数都可以用数轴上的一个点来表示;
④有理数与数轴上的点一一对应.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
例3
考向:利用实数与数轴的关系进行判断
知3-练
感悟新知
解题秘方:利用实数与数轴上的点的对应关系进行解答 .
解:数轴上的任意一点都表示一个实数,可以是有理数,也可以是无理数,故① 错误;
每个实数都可以用数轴上的一个点来表示,故②③正确;
实数与数轴上的点一一对应,故④ 错误.
答案:B
知3-练
感悟新知
3-1. 如图,将面积为 7 的正方形 OABC 和面积为 9 的正方形 ODEF 分别绕原点 O 顺 时 针旋转, 使OA, OD 落在数轴上,点 A, D 在数轴上对应的数分别为 a, b, 则b-a=________ .
变式训练
感悟新知
知4-讲
知识点
实数的性质
4
1. 绝对值:在数轴上,表示一个实数的点到原点的距离称为这个实数的绝对值. 实数a 的绝对值记为|a|.
2. 相反数:对于符号不同而绝对值相等的两个实数,我们称其中一个数是另一个数的相反数,也称这两个数互为相反数. a 的相反数可以表示为-a.
3. 倒数:如果两个实数的积为1,则称这两个实数互为倒数.
知4-讲
感悟新知
特别提醒
在有理数范围内的一些基本概念( 如相反数、倒数、绝对值)在实数范围内依然适用.
感悟新知
知4-练
[母题 教材 P85 练习 T2 ]求下列各数的相反数、倒数和绝对值 .
(1) ;(2) - ;(3)2 - .
例4
考向:利用实数的性质解决实数问题
解题秘方:利用实数的性质求相反数、倒数、绝对值.
知4-练
感悟新知
解: 的相反数是 - ,倒数是 ,绝对值是 .
(1) ;
(2) - ;
(3)2 - .
- =- ,则它的相反数是 ,倒数是-,绝对值是 .
2- 的相反数是 -2,倒数是 ,绝对值是2- .
知4-练
4-1. [中考·青岛]-的相反数是( )
A. - B. -
C. ± D.
D
变式训练
知4-练
感悟新知
4-2. -|- |的值为( )
A. B. -
C. ± D. 2
B
感悟新知
知5-讲
知识点
实数的大小比较
5
1. 实数大小的比较
(1)数轴上的两点,右边的点表示的数总比左边的点表示的数大;
(2)正实数大于0,0 大于负实数,正实数都大于负实数;
(3)两个负实数比较大小,绝对值大的反而小.
感悟新知
知5-讲
2. (1)一般地,对于任意两个正数a 和b,如果 a>b,那么 > , > ;反过来,如果 > 或 > ,那么 a>b.
(2) 一般地,对于任意两个负数a 和b,如果 a>b,那么 > ;反之,如果 > ,那么a>b.
知5-讲
感悟新知
特别提醒
比较两个实数的大小,可以根据题目特点选用不同的方法.
知5-练
感悟新知
[母题 教材 P87 例 1 ] 比较下列各组数的大小:
(1) - 和 - 1.1;(2) - 和 - ;(3)2.2 和 .
例5
考向:实数的大小比较
解题秘方:紧扣实数的比较大小的方法求解 .
知5-练
感悟新知
解:因为 - ≈ - 1.047 2, | - 1.047 2|<| - 1.1|,
所以 - > - 1.1.
(1) - 和 - 1.1
(2) - 和 -
因为 3<7,所以 < ,所以 - > - .
知5-练
感悟新知
解:方法一 (被开方数比较法)
因为 2 .2= = ,而 4.84<5,
所以 2 .2< .
方法 二(平方比较法)
因为 2 .2 2= 4.84,( ) 2=5, 4.84<5,
所以 2 .2< .
(3)2.2 和
已知两个正数 a,b,如果
a< b,那么 < .
已知两个正数 a, b,如
果a2 < b2,那么 a< b.
知5-练
感悟新知
5-1. [ 中考·扬州 ] 已知a= , b=2, c= ,则 a, b, c 的大小关系是( )
A. b>a>c B. a>c>b
C. a>b>c D. b>c>a
C
变式训练
知5-练
感悟新知
5-2.用“<”连接下列各数: - , , - ,2.5, 0.
感悟新知
知6-讲
知识点
确定一个无理数的大致范围
6
根据实数大小比较的方法,对一些不易求值的无理数,我们通常用两边夹逼的方法确定这个无理数的大致范围.
因为12=1,2 2=4,1<2<4,所以1< <2;
取1 与2 之间的一个数,如1.5,1.52=2.2 5,而1<2<2.25,所以1< <1.5;
感悟新知
知6-讲
取1 与1.5 之间的一个数,如1.3,1.32=1.6 9,而1.69<2< 2.2 5,所以1.3< <1.5;
取1.3 与1.5 之间的一个数,如1.4,1.42=1.9 6, 而1.96<2<2.2 5,所以1.4< <1.5.
感悟新知
知6-讲
如果精确到0.1,取1.4 与1.5 之间的一个数,如1.45,1.452=2.102 5,而1.96<2<2.102 5,所以1.4< <1.45,那么≈ 1.4,这样进行下去,我们可以得到 的更精确的近似值.
感悟新知
知6-讲
说明:
(1)运用夹逼的方法确定无理数的大致范围的关键是确定比无理数大(或小)的恰当的有理数;
(2)求无理数的小数部分时,可先确定这个无理数的整数部分,那么原数与整数部分的差就是这个无理数的小数部分.
知5-讲
感悟新知
特别解读
在比较的过程中, 利用了被开方数大的, 其算术平方根也大的 性质.
感悟新知
知6-练
[母题 教材P89 练习T1 ] 已知 a, b 为两个连续整数,且 a<例6
考向:利用估算解决算术平方根问题
5
知6-练
感悟新知
解题秘方:本题运用夹逼法来找出与7 接近的两个平方数,确定 7 的算术平方根的范围,从而确定整数 a 与 b 的值 .
解:因为 2 2< 7<3 2,所以 2< <3.
因为 a, b 为两个连续整数,且 a<所以 a=2, b=3. 所以 a+b=5.
答案:5
知6-练
感悟新知
6-1.估计 的值应在( )
A. 3.5 和 4 之间
B. 4 和 4.5 之间
C. 4.5 和 5 之间
D. 5 和 5.5 之间
C
变式训练
实数
实数
定义
数轴
性质
运算
有理数
无理数
14.3 实 数
第十四章 实 数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
无理数
实数的概念及分类
实数与数轴
实数的性质
实数的大小比较
确定一个无理数的大致范围
知1-讲
感悟新知
知识点
无理数
1
1. 定义
无限不循环小数叫做无理数 .
判断标准: 小数位数无限,小数形式为不循环 .
感悟新知
知1-讲
特别警示
1. 无理数都是无限小数,但无限小数不一定是无理数,只有无限不循环小数才是无理数.例如: 0. 是无限小数,但不是无理数.
2. 某些数的平方根或立方根是无理数,但带根号的数不一定都是无理数 .例如 , 就不是无理数.
感悟新知
2. 三种常见形式
(1)开方开不尽而得到的数,如 , ,…;
(2)含有 π 的一类数,如 π, π, π +1,…;
(3) 以无限不循环小数的形式出现的具有特定结构的数,如0.101 001 000 1…(每相邻两个 1 之间依次多一个 0) .
知1-讲
感悟新知
3. 无理数与有理数的区别
(1) 有理数是有限小数或无限循环小数,而无理数是无限不循环小数;
(2) 所有的有理数都可以写成分数的形式(整数可以看成分母为 1 的分数),而无理数不能写成分数的形式 .
知1-讲
知1-练
感悟新知
考向:利用无理数的定义识别无理数
[母题 教材 P81 练习 T2 ]下列各数:3.141 59, - 3,0.131 131 113…(每相邻两个 3 之间依次多一个 1),
π - 5, +1, - 中,无理数有_______个 .
例1
3
解题秘方:根据无理数的三种常见形式去辨析.
知1-练
感悟新知
解:∵ 3.141 59 是有限小数, ∴ 3.141 59 是有理数 .
∵ - 3= - 2, ∴ - 3是有理数 .
∵ 0.131 131 113…(每相邻两个 3 之间依次多一个 1)是无限不循环小数, ∴ 0.131 131 113…(每相邻两个 3 之间依次多一个 1)是无理数 .
∵ π 是无理数, ∴ π - 5 是无理数 .
∵ 是无理数, ∴ +1 是无理数 .
∵ - 是分数, ∴ - 是有理数 .
知1-练
感悟新知
1-1. [ 中考·长沙 ] 下列各数中,是无理数的是( )
A. B.π
C. -1 D. 0
B
变式训练
知1-练
感悟新知
1-2.在 , 3, ,0.124, 3.141 592 6, 中,无理数有 ________个 .
2
感悟新知
知2-讲
知识点
实数的概念及分类
2
1. 定义 有理数和无理数统称为实数 .
特别解读:在实数范围内,一个数不是有理数,那么它就一定是无理数,反之亦成立.
知2-讲
2. 分类 (1)按定义分类:
实数
有限小数或
无限循环小数
感悟新知
知2-讲
感悟新知
特别提醒
1. 实数的分类有不同的方法,但不论用哪一种分类方法,都要按同一标准,做到不重复不遗漏;
2. 对实数进行分类时, 某些数应先进行计算或化简,然后根据最后的结果进行分类. 不能看到带根号的数,就认为是无理数,也不能看到有分数线的数,就认为是有理数.
感悟新知
知2-讲
实数
0 既不是正实数也不是负实数.
(2) 按性质分类:
知2-练
[母题 教材P84 练习T1] 把下列各数填入相应的大括号内:
-,-,,,- 3,0,-π,-,
-4.201,3.101 001 000 1…(每相邻两个1之间0的个数逐次加1).
有理数:{ …};无理数:{ …};
整数:{ …};分数:{ …};
正实数:{ …};负实数:{ …}.
. .
例2
考向:利用实数中各类数的特征进行分类
知2-练
解题秘方:根据有理数、无理数等概念进行分类时,应注意先把一些数进行化简再判断.
知2-练
解:有理数:{-,,- 3,0, -,
-4. 0,…}.
无理数:{-,,-π,3.101 001 000 1… (每相邻两个1 之间0的个数逐次加1),…}.
判断时要看结果,不要看表面形式,如 - 3 =2是有理数,而不是无理数.
知2-练
整数:{- 3,0, …}.
分数:{-,,-,-4.0,…}.
正实数:{, ,- 3,3.101 001 000 1… (每相邻两个1 之间0的个数逐次加1),…}.
负实数:{-,-,-π,-,-4. 0,…}.
知2-练
. .
. .
2-1. 把下列各数分别填到相应的横线上:
-3.141 519 26,,3 ,,,0.21,0,-3,0.202 002 000 200 002…(每相邻两个2之间0的个数逐次加1).
(1)正有理数:_________________ ;
(2)负无理数: __________________;
(3)负实数: ______________________.
变式训练
知2-练
感悟新知
2-2.在 , - ,3. , - 8, 3, - ,0, -π 中,有理数有 m个,整数有 p 个,分数有 k 个,负数有 t 个,则 m-k+t+p= _________.
9
知3-讲
知识点
实数与数轴
3
实数与数轴间的关系
实数与数轴上的点是一一对应的.
“一一对应”包含着两层含义:
①每一个实数都可以用数轴上的一个点来表示;
②数轴上的每一个点都表示一个实数.
知3-讲
感悟新知
特别解读
借助数轴上的点可以把实数直观地表示出来,数轴上的任意一点表示的数,不是有理数就是无理数.
知3-练
感悟新知
下列说法正确的有( )
①数轴上的任意一点都表示一个有理数;
②每个无理数都可以用数轴上的一个点来表示;
③任意一个实数都可以用数轴上的一个点来表示;
④有理数与数轴上的点一一对应.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
例3
考向:利用实数与数轴的关系进行判断
知3-练
感悟新知
解题秘方:利用实数与数轴上的点的对应关系进行解答 .
解:数轴上的任意一点都表示一个实数,可以是有理数,也可以是无理数,故① 错误;
每个实数都可以用数轴上的一个点来表示,故②③正确;
实数与数轴上的点一一对应,故④ 错误.
答案:B
知3-练
感悟新知
3-1. 如图,将面积为 7 的正方形 OABC 和面积为 9 的正方形 ODEF 分别绕原点 O 顺 时 针旋转, 使OA, OD 落在数轴上,点 A, D 在数轴上对应的数分别为 a, b, 则b-a=________ .
变式训练
感悟新知
知4-讲
知识点
实数的性质
4
1. 绝对值:在数轴上,表示一个实数的点到原点的距离称为这个实数的绝对值. 实数a 的绝对值记为|a|.
2. 相反数:对于符号不同而绝对值相等的两个实数,我们称其中一个数是另一个数的相反数,也称这两个数互为相反数. a 的相反数可以表示为-a.
3. 倒数:如果两个实数的积为1,则称这两个实数互为倒数.
知4-讲
感悟新知
特别提醒
在有理数范围内的一些基本概念( 如相反数、倒数、绝对值)在实数范围内依然适用.
感悟新知
知4-练
[母题 教材 P85 练习 T2 ]求下列各数的相反数、倒数和绝对值 .
(1) ;(2) - ;(3)2 - .
例4
考向:利用实数的性质解决实数问题
解题秘方:利用实数的性质求相反数、倒数、绝对值.
知4-练
感悟新知
解: 的相反数是 - ,倒数是 ,绝对值是 .
(1) ;
(2) - ;
(3)2 - .
- =- ,则它的相反数是 ,倒数是-,绝对值是 .
2- 的相反数是 -2,倒数是 ,绝对值是2- .
知4-练
4-1. [中考·青岛]-的相反数是( )
A. - B. -
C. ± D.
D
变式训练
知4-练
感悟新知
4-2. -|- |的值为( )
A. B. -
C. ± D. 2
B
感悟新知
知5-讲
知识点
实数的大小比较
5
1. 实数大小的比较
(1)数轴上的两点,右边的点表示的数总比左边的点表示的数大;
(2)正实数大于0,0 大于负实数,正实数都大于负实数;
(3)两个负实数比较大小,绝对值大的反而小.
感悟新知
知5-讲
2. (1)一般地,对于任意两个正数a 和b,如果 a>b,那么 > , > ;反过来,如果 > 或 > ,那么 a>b.
(2) 一般地,对于任意两个负数a 和b,如果 a>b,那么 > ;反之,如果 > ,那么a>b.
知5-讲
感悟新知
特别提醒
比较两个实数的大小,可以根据题目特点选用不同的方法.
知5-练
感悟新知
[母题 教材 P87 例 1 ] 比较下列各组数的大小:
(1) - 和 - 1.1;(2) - 和 - ;(3)2.2 和 .
例5
考向:实数的大小比较
解题秘方:紧扣实数的比较大小的方法求解 .
知5-练
感悟新知
解:因为 - ≈ - 1.047 2, | - 1.047 2|<| - 1.1|,
所以 - > - 1.1.
(1) - 和 - 1.1
(2) - 和 -
因为 3<7,所以 < ,所以 - > - .
知5-练
感悟新知
解:方法一 (被开方数比较法)
因为 2 .2= = ,而 4.84<5,
所以 2 .2< .
方法 二(平方比较法)
因为 2 .2 2= 4.84,( ) 2=5, 4.84<5,
所以 2 .2< .
(3)2.2 和
已知两个正数 a,b,如果
a< b,那么 < .
已知两个正数 a, b,如
果a2 < b2,那么 a< b.
知5-练
感悟新知
5-1. [ 中考·扬州 ] 已知a= , b=2, c= ,则 a, b, c 的大小关系是( )
A. b>a>c B. a>c>b
C. a>b>c D. b>c>a
C
变式训练
知5-练
感悟新知
5-2.用“<”连接下列各数: - , , - ,2.5, 0.
感悟新知
知6-讲
知识点
确定一个无理数的大致范围
6
根据实数大小比较的方法,对一些不易求值的无理数,我们通常用两边夹逼的方法确定这个无理数的大致范围.
因为12=1,2 2=4,1<2<4,所以1< <2;
取1 与2 之间的一个数,如1.5,1.52=2.2 5,而1<2<2.25,所以1< <1.5;
感悟新知
知6-讲
取1 与1.5 之间的一个数,如1.3,1.32=1.6 9,而1.69<2< 2.2 5,所以1.3< <1.5;
取1.3 与1.5 之间的一个数,如1.4,1.42=1.9 6, 而1.96<2<2.2 5,所以1.4< <1.5.
感悟新知
知6-讲
如果精确到0.1,取1.4 与1.5 之间的一个数,如1.45,1.452=2.102 5,而1.96<2<2.102 5,所以1.4< <1.45,那么≈ 1.4,这样进行下去,我们可以得到 的更精确的近似值.
感悟新知
知6-讲
说明:
(1)运用夹逼的方法确定无理数的大致范围的关键是确定比无理数大(或小)的恰当的有理数;
(2)求无理数的小数部分时,可先确定这个无理数的整数部分,那么原数与整数部分的差就是这个无理数的小数部分.
知5-讲
感悟新知
特别解读
在比较的过程中, 利用了被开方数大的, 其算术平方根也大的 性质.
感悟新知
知6-练
[母题 教材P89 练习T1 ] 已知 a, b 为两个连续整数,且 a<
考向:利用估算解决算术平方根问题
5
知6-练
感悟新知
解题秘方:本题运用夹逼法来找出与7 接近的两个平方数,确定 7 的算术平方根的范围,从而确定整数 a 与 b 的值 .
解:因为 2 2< 7<3 2,所以 2< <3.
因为 a, b 为两个连续整数,且 a<
答案:5
知6-练
感悟新知
6-1.估计 的值应在( )
A. 3.5 和 4 之间
B. 4 和 4.5 之间
C. 4.5 和 5 之间
D. 5 和 5.5 之间
C
变式训练
实数
实数
定义
数轴
性质
运算
有理数
无理数
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
