湖南省怀化市九县十校2025届九年级下学期“新课标+新中考“联合调研考试数学试卷(含答案)
文档属性
| 名称 | 湖南省怀化市九县十校2025届九年级下学期“新课标+新中考“联合调研考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 600.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 18:07:24 | ||
图片预览



文档简介
2025年上学期九县十校“新课标·新中考”联合调研考试
九年级 数学
满分:120分 考试用时:120分钟
一、单选题(共10小题,每小题3分,共30分)
1.2的相反数是( )
A. B. C.2 D.
2.袋中装有3个白球,1个红球.从中一次性取出2个球,下列事件是必然事件的是( )
A.两个球都是白球. B.两个球都是红球.
C.两个球中至少有一个是白球. D.两个球中至少有一个是红球.
3.截止到5月份,《哪吒2》全球总票房已突破158亿元,位居全球动画电影票房榜第1名,全球影视票房榜第4位.数据“158亿”用科学记数法可表示为( )
A. B. C. D.
4.下列各点中,不在反比例函数 的图像上的点是( )
A.(,) B.(,) C.(,) D.(,)
5.如右图,用两块相同三角板按如图所示的方式作平行线和,能解释其中道理的依据( )
A.内错角相等,两直线平行 B.同位角相等,两直线平行
C.同旁内角互补,两直线平行 D.平行于同一直线的两条直线平行
6.计算的结果是( )
A. B. C. D.
7.凸透镜成像的原理如图所示,∥∥,若焦点 到物体的距离与到凸透镜的中心之比是6:5,若物体,则其像的长是( )
A. B. C. D.
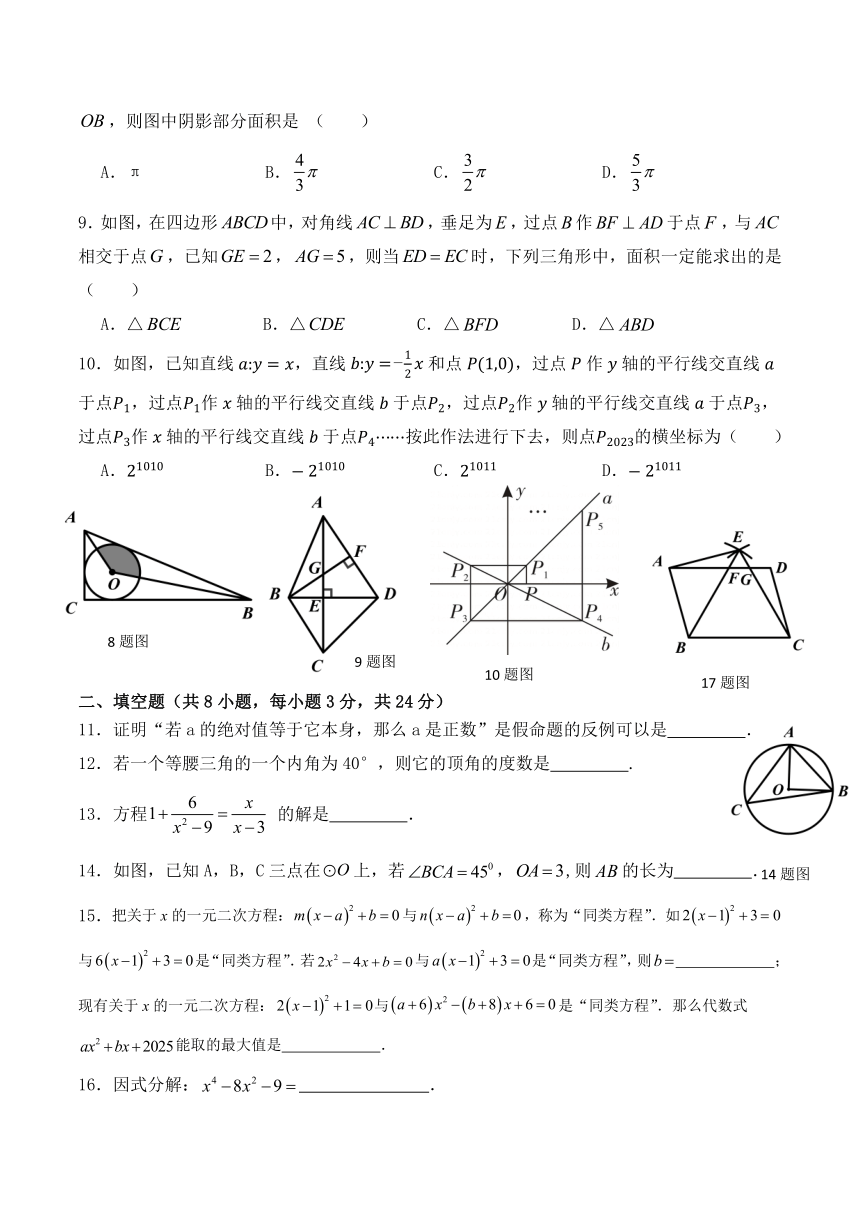
8.如图,在△中,∠,,,△的内切圆,连接,,则图中阴影部分面积是 ( )
A.π B. C. D.
9.如图,在四边形中,对角线,垂足为,过点作于点,与相交于点,已知,,则当时,下列三角形中,面积一定能求出的是( )
A.△ B.△ C.△ D.△
10.如图,已知直线,直线和点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点按此作法进行下去,则点的横坐标为( )
A. B. C. D.
(
8题图
)
(
17题图
) (
10题图
) (
9题图
)
二、填空题(共8小题,每小题3分,共24分)
11.证明“若a的绝对值等于它本身,那么a是正数”是假命题的反例可以是 .
12.若一个等腰三角的一个内角为40°,则它的顶角的度数是 .
13.方程 的解是 .
(
14题图
)14.如图,已知A,B,C三点在上,若,,则的长为 .
15.把关于x的一元二次方程:与,称为“同类方程”.如与是“同类方程”.若与是“同类方程”,则 ;现有关于x的一元二次方程:与是“同类方程”.那么代数式能取的最大值是 .
16.因式分解: .
17.在平行四边形ABCD中,分别以点B、C为圆心,大于为半径画弧,两弧交于点E,连接BE,CE,AE.若AE=CD,∠BCE=60°,BC=6,AG=4,则AB= .
18.在学习了“利用函数的图象研究函数”后,为了研究函数的性质,小明用描点法画它的图象,列出了如下表格:
… …
… …
下列五个结论:①点(5,)在该函数图象上;②该函数图象在轴的下方;③该函数图象有最高点;④若(,)和 (,)是该函数图象上两点,则;⑤若将该函数图象向左平移1个单位长度,则平移后的图象的函数表达式是.
其中正确的结论是 .(填写序号)
三、解答题(共8道题,共66分)
19.(满分6分)计算:
(
①
②
)20.(满分6分)解不等式组: .
21.(满分8分,每小题4分)
如图,,,,.
(1)试说明:;
(2)求的度数.
22.(满分8分)促进青少年健康成长是实施“健康中国”战略的重要内容.为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了如下的表格和统计图:
等级 次数 频率
不合格
合格
良好
优秀 a
请结合上述信息完成下列问题:
(1) , ;
(2)若该校有2000名学生,估计该校学生一分钟跳绳次数达到合格的人数;
(3)本次比赛“优秀”等级学生中,有4位同学一分钟跳绳的次数达175次以上,其中男生和女生各占一半,现准备从这四位同学中选2位参加比赛,请用列表或画树状图的方法,求选出的2位同学恰好性别相同的概率.
23.(满分8分)物理中有这样一个问题:“如图1示意图所示,均匀杆长为,杆可以绕转轴点在竖直平面内自由转动,在点正上方距离为处固定一个小定滑轮,细绳通过定滑轮与杆的另一端相连,并将杆从水平位置缓慢向上拉起.当杆与水平面夹角为时,求动力臂.从数学角度看是这样一个问题:如图2,已知于点且,连接,求点到的距离.
请写出解答过程求出点到的距离.(结果保留根号)
(
图1
) (
图2
)
24.(满分8分) 【问题背景】某科研机构准备种植一种药材,收集信息如下:
①单位面积产量(单位:)与种植面积(单位:亩)的关系为:;
②种植成本(单位:万元)与种植面积(单位:亩)的关系为:;
③销售价格:0.08万元.
【问题解决】(1)求总产量为7200时的种植面积;
(2)求该科研机构种植这种药材能获得的最大利润;
(3)该科研机构计划种植这种药材的成本不超过180万元,所获利润不低于300万元,直接写出种植面积的范围.
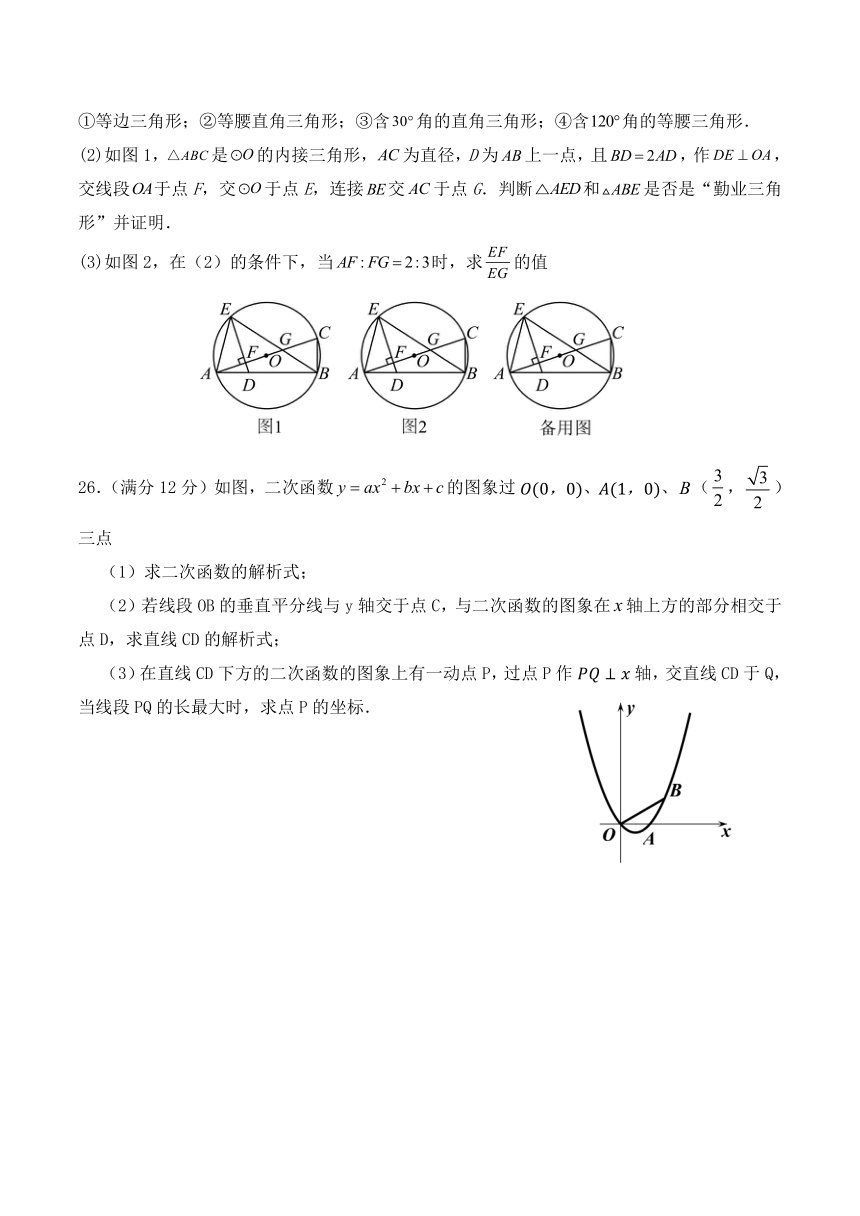
25.(满分10分) 有两边之比为的三角形叫做“勤业三角形”.
(1)下列各三角形中,一定是“勤业三角形”的是________;(填序号)
①等边三角形;②等腰直角三角形;③含角的直角三角形;④含角的等腰三角形.
(2)如图1,是的内接三角形,为直径,D为上一点,且,作,交线段于点F,交于点E,连接交于点G.判断和是否是“勤业三角形”并证明.
(3)如图2,在(2)的条件下,当时,求的值
26.(满分12分)如图,二次函数的图象过、、(,)三点
(1)求二次函数的解析式;
(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在轴上方的部分相交于点D,求直线CD的解析式;
(3)在直线CD下方的二次函数的图象上有一动点P,过点P作轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
答案解析部分
一、选择题
1—5. DCCBA 6—10. DCCAD
二、填空题
11. 12.40°或100° 13. 14.
15. 5;2026 16. 17. 18.①③⑤
三、解答题
19.解:
=3-1+…………………………………………………………………3分
=…………………………………………………………………………6分
20.解: 解不等式①得, ……………………………………….2分
解不等式②得, …………………………………….4分
∴原不等式组的解集是…………………………………….6分
21.解:(1)证明:∵,
∴,即…………….2分
在和中,
,
∴………………………………………..4分
(2)由(1)证得……………………………………………6分
∵,∴.……………………………………8分
22.解:(1)0.25;14……………………………………2分
(2)1800人………………………………………4分
(3)………………………………………………8分
23.解:过点分别作于,于.
在△中,,,
∴, ……………………..4分
在△中,,
∴ ………………………………………………………….6分
设点到的距离为,则,即 ,解得 …8分
24. 解:(1)根据题意得
,解得
所以,种植面积为7200时的种植面积为12亩……………………………………3分
(2)设种植这种药材的利润为,则根据题意得
……………………………………………………………5分
∵ ,∴当时,最大,最大值为400……………………………………6分
(
①
②
) (3)根据题意有
解不等式①得,
解不等式②得,
∴种植面积的范围是 ………………………………………………………8分
25.(1)解:③④;……………………………………………………………………………2分
(2)解:和△都是“勤业三角形”,
证明如下:
如图:连接,设,
∴,
,
∴,
又,
,即,
,又,
,,
,…………………………………………………………………………4分
,,,,
和都是“勤业三角形”;………………………………………………6分
(3)解:如图:过点G作交于点I,
,
,
,
,
,
,……………………………………………………………8分
设,
由(2)知,,
,
,
,
,
在中,.………………………………………………10分
26.(1)解:根据题意得
,解得 ,所以该二次函数的解析式为 ………4分
(2)过点B作BE⊥轴,垂足为E
在△中,,∴
在△中,,∴
∵,,∴,∴ …………………………………….6分
∴OB的垂直平分线必过点A(1,0)且平分
∴ ,∴
∴C点的坐标是(0, )………………………………………………………………………..8分
设直线CD的解析式为 ,则 ,解得,
∴直线CD的解析式为
(3)设(m,),(m,)且
…………………………………………………10分
∴当 时,有最大值,此时(,)……………………………..12分
九年级 数学
满分:120分 考试用时:120分钟
一、单选题(共10小题,每小题3分,共30分)
1.2的相反数是( )
A. B. C.2 D.
2.袋中装有3个白球,1个红球.从中一次性取出2个球,下列事件是必然事件的是( )
A.两个球都是白球. B.两个球都是红球.
C.两个球中至少有一个是白球. D.两个球中至少有一个是红球.
3.截止到5月份,《哪吒2》全球总票房已突破158亿元,位居全球动画电影票房榜第1名,全球影视票房榜第4位.数据“158亿”用科学记数法可表示为( )
A. B. C. D.
4.下列各点中,不在反比例函数 的图像上的点是( )
A.(,) B.(,) C.(,) D.(,)
5.如右图,用两块相同三角板按如图所示的方式作平行线和,能解释其中道理的依据( )
A.内错角相等,两直线平行 B.同位角相等,两直线平行
C.同旁内角互补,两直线平行 D.平行于同一直线的两条直线平行
6.计算的结果是( )
A. B. C. D.
7.凸透镜成像的原理如图所示,∥∥,若焦点 到物体的距离与到凸透镜的中心之比是6:5,若物体,则其像的长是( )
A. B. C. D.
8.如图,在△中,∠,,,△的内切圆,连接,,则图中阴影部分面积是 ( )
A.π B. C. D.
9.如图,在四边形中,对角线,垂足为,过点作于点,与相交于点,已知,,则当时,下列三角形中,面积一定能求出的是( )
A.△ B.△ C.△ D.△
10.如图,已知直线,直线和点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点按此作法进行下去,则点的横坐标为( )
A. B. C. D.
(
8题图
)
(
17题图
) (
10题图
) (
9题图
)
二、填空题(共8小题,每小题3分,共24分)
11.证明“若a的绝对值等于它本身,那么a是正数”是假命题的反例可以是 .
12.若一个等腰三角的一个内角为40°,则它的顶角的度数是 .
13.方程 的解是 .
(
14题图
)14.如图,已知A,B,C三点在上,若,,则的长为 .
15.把关于x的一元二次方程:与,称为“同类方程”.如与是“同类方程”.若与是“同类方程”,则 ;现有关于x的一元二次方程:与是“同类方程”.那么代数式能取的最大值是 .
16.因式分解: .
17.在平行四边形ABCD中,分别以点B、C为圆心,大于为半径画弧,两弧交于点E,连接BE,CE,AE.若AE=CD,∠BCE=60°,BC=6,AG=4,则AB= .
18.在学习了“利用函数的图象研究函数”后,为了研究函数的性质,小明用描点法画它的图象,列出了如下表格:
… …
… …
下列五个结论:①点(5,)在该函数图象上;②该函数图象在轴的下方;③该函数图象有最高点;④若(,)和 (,)是该函数图象上两点,则;⑤若将该函数图象向左平移1个单位长度,则平移后的图象的函数表达式是.
其中正确的结论是 .(填写序号)
三、解答题(共8道题,共66分)
19.(满分6分)计算:
(
①
②
)20.(满分6分)解不等式组: .
21.(满分8分,每小题4分)
如图,,,,.
(1)试说明:;
(2)求的度数.
22.(满分8分)促进青少年健康成长是实施“健康中国”战略的重要内容.为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了如下的表格和统计图:
等级 次数 频率
不合格
合格
良好
优秀 a
请结合上述信息完成下列问题:
(1) , ;
(2)若该校有2000名学生,估计该校学生一分钟跳绳次数达到合格的人数;
(3)本次比赛“优秀”等级学生中,有4位同学一分钟跳绳的次数达175次以上,其中男生和女生各占一半,现准备从这四位同学中选2位参加比赛,请用列表或画树状图的方法,求选出的2位同学恰好性别相同的概率.
23.(满分8分)物理中有这样一个问题:“如图1示意图所示,均匀杆长为,杆可以绕转轴点在竖直平面内自由转动,在点正上方距离为处固定一个小定滑轮,细绳通过定滑轮与杆的另一端相连,并将杆从水平位置缓慢向上拉起.当杆与水平面夹角为时,求动力臂.从数学角度看是这样一个问题:如图2,已知于点且,连接,求点到的距离.
请写出解答过程求出点到的距离.(结果保留根号)
(
图1
) (
图2
)
24.(满分8分) 【问题背景】某科研机构准备种植一种药材,收集信息如下:
①单位面积产量(单位:)与种植面积(单位:亩)的关系为:;
②种植成本(单位:万元)与种植面积(单位:亩)的关系为:;
③销售价格:0.08万元.
【问题解决】(1)求总产量为7200时的种植面积;
(2)求该科研机构种植这种药材能获得的最大利润;
(3)该科研机构计划种植这种药材的成本不超过180万元,所获利润不低于300万元,直接写出种植面积的范围.
25.(满分10分) 有两边之比为的三角形叫做“勤业三角形”.
(1)下列各三角形中,一定是“勤业三角形”的是________;(填序号)
①等边三角形;②等腰直角三角形;③含角的直角三角形;④含角的等腰三角形.
(2)如图1,是的内接三角形,为直径,D为上一点,且,作,交线段于点F,交于点E,连接交于点G.判断和是否是“勤业三角形”并证明.
(3)如图2,在(2)的条件下,当时,求的值
26.(满分12分)如图,二次函数的图象过、、(,)三点
(1)求二次函数的解析式;
(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在轴上方的部分相交于点D,求直线CD的解析式;
(3)在直线CD下方的二次函数的图象上有一动点P,过点P作轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
答案解析部分
一、选择题
1—5. DCCBA 6—10. DCCAD
二、填空题
11. 12.40°或100° 13. 14.
15. 5;2026 16. 17. 18.①③⑤
三、解答题
19.解:
=3-1+…………………………………………………………………3分
=…………………………………………………………………………6分
20.解: 解不等式①得, ……………………………………….2分
解不等式②得, …………………………………….4分
∴原不等式组的解集是…………………………………….6分
21.解:(1)证明:∵,
∴,即…………….2分
在和中,
,
∴………………………………………..4分
(2)由(1)证得……………………………………………6分
∵,∴.……………………………………8分
22.解:(1)0.25;14……………………………………2分
(2)1800人………………………………………4分
(3)………………………………………………8分
23.解:过点分别作于,于.
在△中,,,
∴, ……………………..4分
在△中,,
∴ ………………………………………………………….6分
设点到的距离为,则,即 ,解得 …8分
24. 解:(1)根据题意得
,解得
所以,种植面积为7200时的种植面积为12亩……………………………………3分
(2)设种植这种药材的利润为,则根据题意得
……………………………………………………………5分
∵ ,∴当时,最大,最大值为400……………………………………6分
(
①
②
) (3)根据题意有
解不等式①得,
解不等式②得,
∴种植面积的范围是 ………………………………………………………8分
25.(1)解:③④;……………………………………………………………………………2分
(2)解:和△都是“勤业三角形”,
证明如下:
如图:连接,设,
∴,
,
∴,
又,
,即,
,又,
,,
,…………………………………………………………………………4分
,,,,
和都是“勤业三角形”;………………………………………………6分
(3)解:如图:过点G作交于点I,
,
,
,
,
,
,……………………………………………………………8分
设,
由(2)知,,
,
,
,
,
在中,.………………………………………………10分
26.(1)解:根据题意得
,解得 ,所以该二次函数的解析式为 ………4分
(2)过点B作BE⊥轴,垂足为E
在△中,,∴
在△中,,∴
∵,,∴,∴ …………………………………….6分
∴OB的垂直平分线必过点A(1,0)且平分
∴ ,∴
∴C点的坐标是(0, )………………………………………………………………………..8分
设直线CD的解析式为 ,则 ,解得,
∴直线CD的解析式为
(3)设(m,),(m,)且
…………………………………………………10分
∴当 时,有最大值,此时(,)……………………………..12分
同课章节目录
