【期末热点.重难点】用样本估计总体(含解析)2024-2025学年人教A版(2019)数学高一下册
文档属性
| 名称 | 【期末热点.重难点】用样本估计总体(含解析)2024-2025学年人教A版(2019)数学高一下册 |  | |
| 格式 | docx | ||
| 文件大小 | 726.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 16:42:57 | ||
图片预览

文档简介
期末热点.重难点 用样本估计总体
一.选择题(共5小题)
1.(2024秋 辽宁期末)某地有9个快递收件点,在某天接收的快递个数分别为361,285,293,305,403,189,247,265,289,则这组数据的第72百分位数为( )
A.289 B.299 C.305 D.361
2.(2024秋 喀什市期末)已知一组数据3,7,11,7,13,15,则该组数据的第40百分位数为( )
A.7 B.9 C.11 D.12
3.(2025 聊城校级模拟)利用微信转账余额提醒这一小程序从数据库中得到某人一天内的网上交易额如下:26,32,7,13,42,114,则该组数据的平均数为( )
A.36 B.39 C.40 D.41
4.(2025 福建模拟)市环保局开展了环境治理专项活动,活动结束后对志愿者做了一次随机抽样调查,统计整理了部分志愿者的服务时长(单位:小时),得到如图所示的频率分布直方图,据此估计志愿者服务时长的第90百分位数为( )
A.36 B.37 C.38 D.39
5.(2025 温州模拟)已知4名学生的期中考试数学成绩分别为98,110,m,120,且上四分位数为118,则m=( )
A.115 B.116 C.117 D.118
二.多选题(共4小题)
(多选)6.(2025 江西模拟)关于下列命题,说法正确的是( )
A.若f(x)为奇函数,则f(0)=0
B.“x≥1”是“x2≥x”的充分不必要条件
C.命题p: x∈R,x2﹣2024x+2026>0,则命题p的否定为 x∈R,x2﹣2024x+2026≤0
D.已知数据87,72,75,85,87,90,75,78,86,79,则这组数据的40%分位数是78
(多选)7.(2024秋 抚州期末)下列说法正确的是( )
A.数据12,13,14,15,17,19,23,24,27,30的65%分位数是23
B.若样本数据x1,x2,…,x10的方差为8,则数据2x1﹣1,2x2﹣1,…,2x10﹣1的方差为16
C.函数f(x+1)的定义域为[0,1],则f(3x)的定义域为[3,9]
D.若2a=3b=12,则的值为1
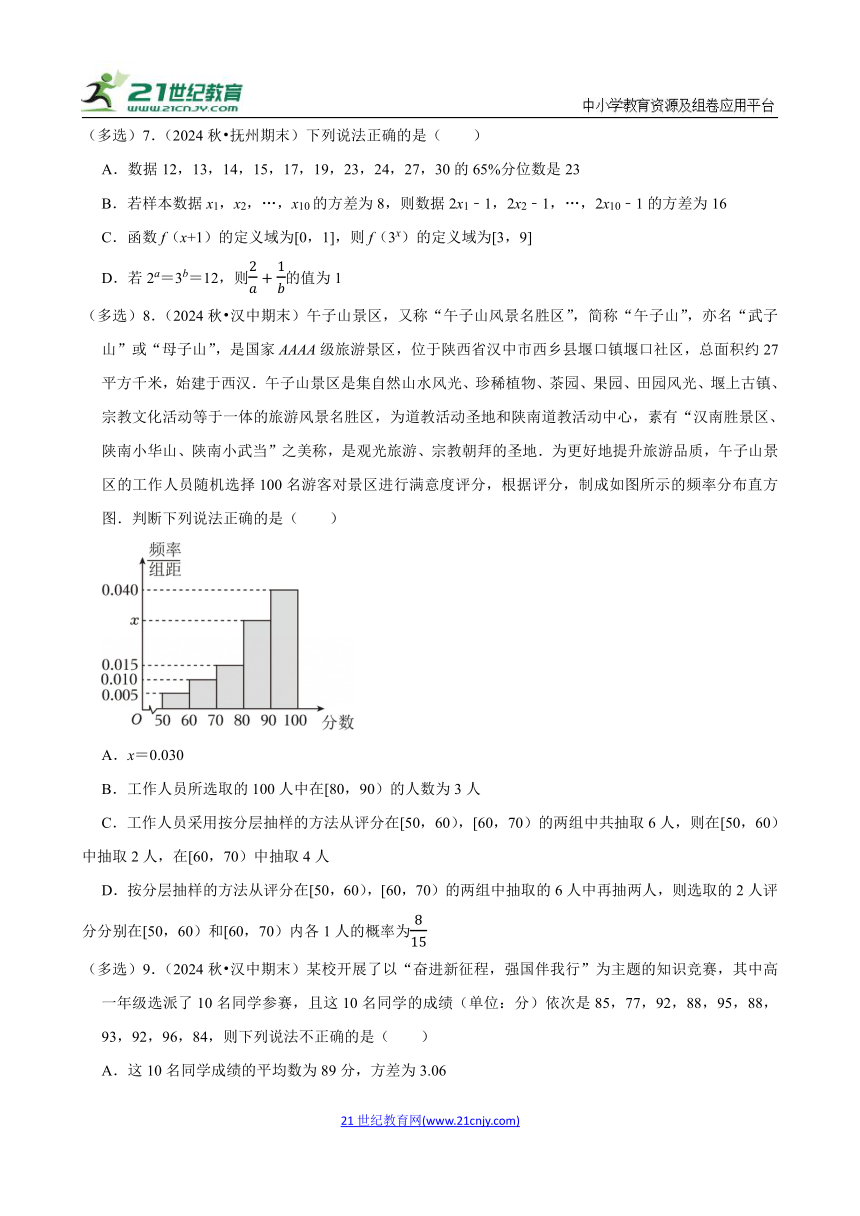
(多选)8.(2024秋 汉中期末)午子山景区,又称“午子山风景名胜区”,简称“午子山”,亦名“武子山”或“母子山”,是国家AAAA级旅游景区,位于陕西省汉中市西乡县堰口镇堰口社区,总面积约27平方千米,始建于西汉.午子山景区是集自然山水风光、珍稀植物、茶园、果园、田园风光、堰上古镇、宗教文化活动等于一体的旅游风景名胜区,为道教活动圣地和陕南道教活动中心,素有“汉南胜景区、陕南小华山、陕南小武当”之美称,是观光旅游、宗教朝拜的圣地.为更好地提升旅游品质,午子山景区的工作人员随机选择100名游客对景区进行满意度评分,根据评分,制成如图所示的频率分布直方图.判断下列说法正确的是( )
A.x=0.030
B.工作人员所选取的100人中在[80,90)的人数为3人
C.工作人员采用按分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,则在[50,60)中抽取2人,在[60,70)中抽取4人
D.按分层抽样的方法从评分在[50,60),[60,70)的两组中抽取的6人中再抽两人,则选取的2人评分分别在[50,60)和[60,70)内各1人的概率为
(多选)9.(2024秋 汉中期末)某校开展了以“奋进新征程,强国伴我行”为主题的知识竞赛,其中高一年级选派了10名同学参赛,且这10名同学的成绩(单位:分)依次是85,77,92,88,95,88,93,92,96,84,则下列说法不正确的是( )
A.这10名同学成绩的平均数为89分,方差为3.06
B.这10名同学成绩的中位数为92分,众数为88分和92分
C.这10名同学成绩的极差为18分
D.这10名同学成绩的75%分位数为93分
三.填空题(共3小题)
10.(2024秋 牡丹江期末)若样本数据x1,x2,x3,x4,x5的平均数为2,则数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3的平均数为 .
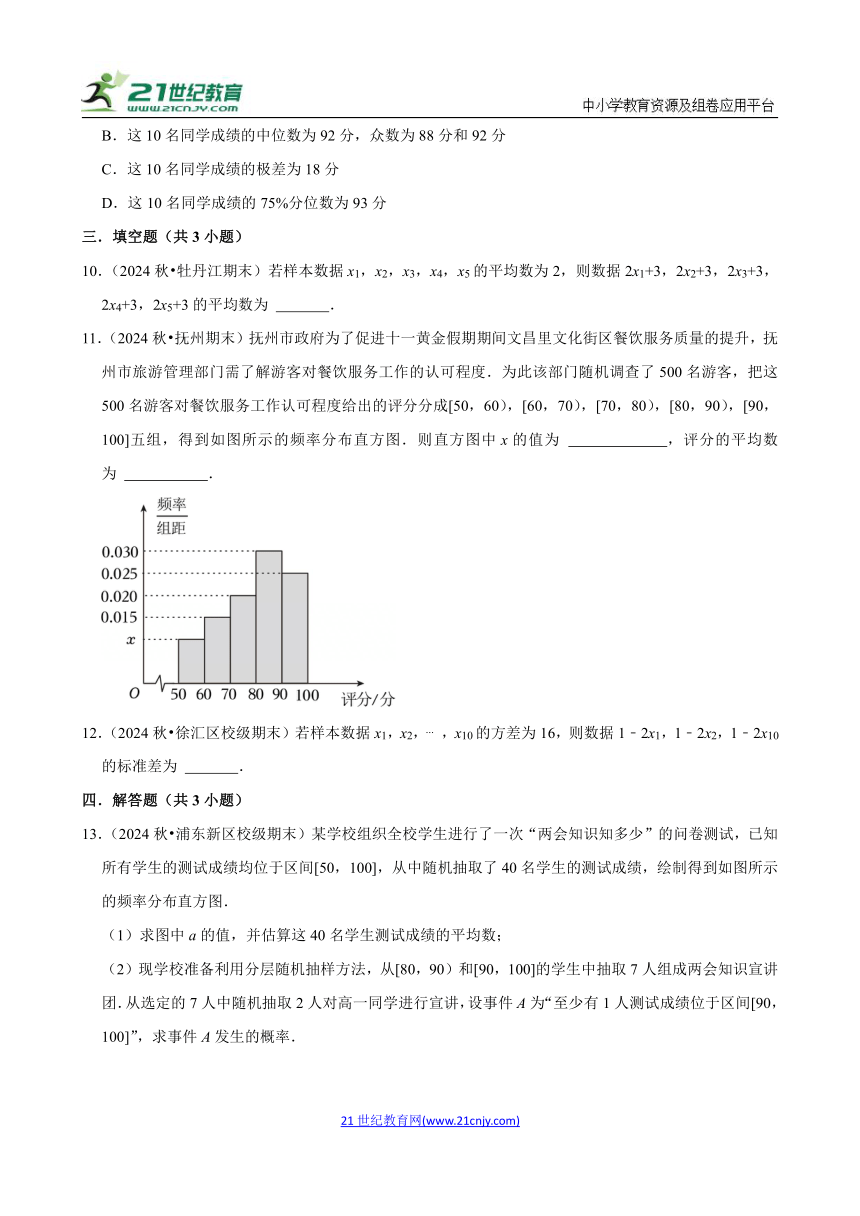
11.(2024秋 抚州期末)抚州市政府为了促进十一黄金假期期间文昌里文化街区餐饮服务质量的提升,抚州市旅游管理部门需了解游客对餐饮服务工作的认可程度.为此该部门随机调查了500名游客,把这500名游客对餐饮服务工作认可程度给出的评分分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示的频率分布直方图.则直方图中x的值为 ,评分的平均数为 .
12.(2024秋 徐汇区校级期末)若样本数据x1,x2, ,x10的方差为16,则数据1﹣2x1,1﹣2x2,1﹣2x10的标准差为 .
四.解答题(共3小题)
13.(2024秋 浦东新区校级期末)某学校组织全校学生进行了一次“两会知识知多少”的问卷测试,已知所有学生的测试成绩均位于区间[50,100],从中随机抽取了40名学生的测试成绩,绘制得到如图所示的频率分布直方图.
(1)求图中a的值,并估算这40名学生测试成绩的平均数;
(2)现学校准备利用分层随机抽样方法,从[80,90)和[90,100]的学生中抽取7人组成两会知识宣讲团.从选定的7人中随机抽取2人对高一同学进行宣讲,设事件A为“至少有1人测试成绩位于区间[90,100]”,求事件A发生的概率.
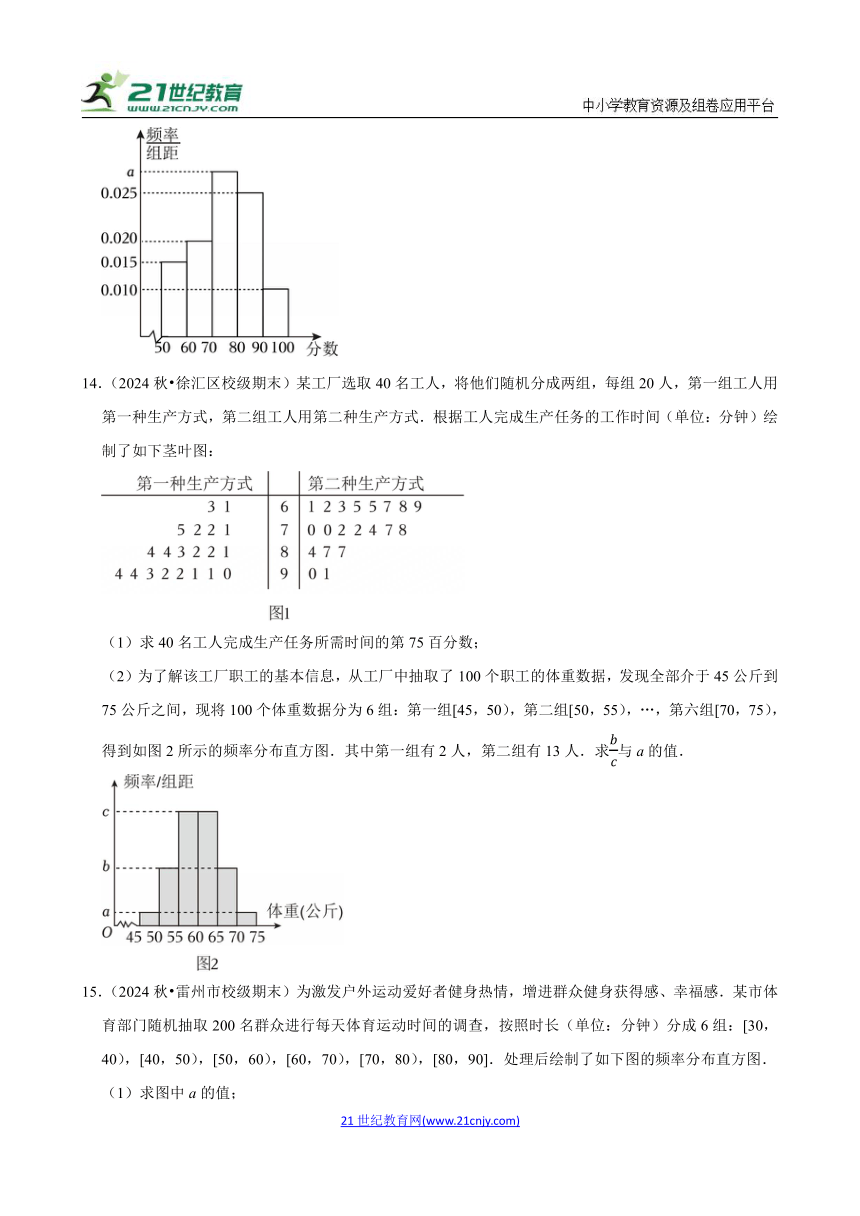
14.(2024秋 徐汇区校级期末)某工厂选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:分钟)绘制了如下茎叶图:
(1)求40名工人完成生产任务所需时间的第75百分数;
(2)为了解该工厂职工的基本信息,从工厂中抽取了100个职工的体重数据,发现全部介于45公斤到75公斤之间,现将100个体重数据分为6组:第一组[45,50),第二组[50,55),…,第六组[70,75),得到如图2所示的频率分布直方图.其中第一组有2人,第二组有13人.求与a的值.
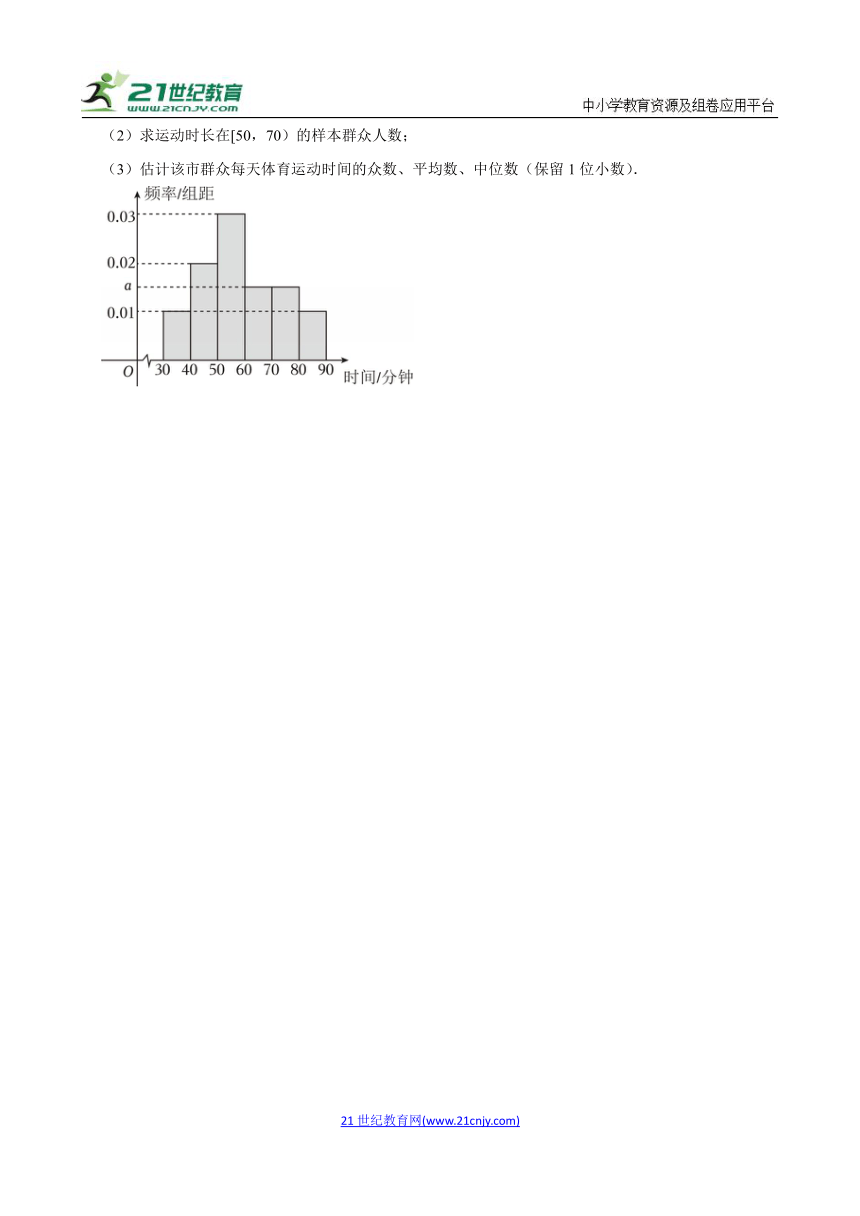
15.(2024秋 雷州市校级期末)为激发户外运动爱好者健身热情,增进群众健身获得感、幸福感.某市体育部门随机抽取200名群众进行每天体育运动时间的调查,按照时长(单位:分钟)分成6组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90].处理后绘制了如下图的频率分布直方图.
(1)求图中a的值;
(2)求运动时长在[50,70)的样本群众人数;
(3)估计该市群众每天体育运动时间的众数、平均数、中位数(保留1位小数).
期末热点.重难点 用样本估计总体
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 辽宁期末)某地有9个快递收件点,在某天接收的快递个数分别为361,285,293,305,403,189,247,265,289,则这组数据的第72百分位数为( )
A.289 B.299 C.305 D.361
【考点】百分位数.
【专题】转化思想;分析法;概率与统计;运算求解.
【答案】C
【分析】根据百分位数的估计方法计算即可.
【解答】解:将这组数据361,285,293,305,403,189,247,265,289,
按照从小到大的顺序排列得189,247,265,285,289,293,305,361,403,
因为9×0.72=6.48,所以这组数据的第72百分位数为第7个数305.
故选:C.
【点评】本题考查百分位数的定义,是基础题.
2.(2024秋 喀什市期末)已知一组数据3,7,11,7,13,15,则该组数据的第40百分位数为( )
A.7 B.9 C.11 D.12
【考点】百分位数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】A
【分析】根据百分位数的定义直接计算.
【解答】解:一组数据3,7,11,7,13,15,
将数据从小到大排列得到:3,7,7,11,13,15,
∵6×0.4=2.4,
∴这组数据的第40百分位数为第三个数据7.
故选:A.
【点评】本题考查百分位数的定义等基础知识,考查运算求解能力,是基础题.
3.(2025 聊城校级模拟)利用微信转账余额提醒这一小程序从数据库中得到某人一天内的网上交易额如下:26,32,7,13,42,114,则该组数据的平均数为( )
A.36 B.39 C.40 D.41
【考点】平均数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】B
【分析】利用平均数的计算公式直接计算即可.
【解答】解:根据平均数的定义可得,该组数据的平均数为39.
故选:B.
【点评】本题考查平均数的应用,属于基础题.
4.(2025 福建模拟)市环保局开展了环境治理专项活动,活动结束后对志愿者做了一次随机抽样调查,统计整理了部分志愿者的服务时长(单位:小时),得到如图所示的频率分布直方图,据此估计志愿者服务时长的第90百分位数为( )
A.36 B.37 C.38 D.39
【考点】百分位数.
【专题】数形结合;数形结合法;概率与统计;运算求解.
【答案】C
【分析】利用频率分布直方图的性质求出a的值,再结合第90百分位数定义求解即可.
【解答】解:由题意得组距为24﹣20=4,
∵小长方形面积和为1,∴4×(0.005+0.065+0.040+0.090+a)=1,
解得a=0.050,
∵4×(0.005+0.065+0.040+0.090)=0.8,
∴第90百分位数在[36,40]内,
设第90百分位数为x,
得到0.8+0.05(x﹣36)=0.9,解得x=38.
故选:C.
【点评】本题考查频率分布直方图的性质、百分位数等基础知识,考查运算求解能力,是基础题.
5.(2025 温州模拟)已知4名学生的期中考试数学成绩分别为98,110,m,120,且上四分位数为118,则m=( )
A.115 B.116 C.117 D.118
【考点】百分位数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】B
【分析】利用百分位数定义求解.
【解答】解:4名学生的期中考试数学成绩分别为98,110,m,120,且上四分位数为118,
4×75%=3是整数,∴,得m=116.
故选:B.
【点评】本题考查百分位数定义等基础知识,考查运算求解能力,是基础题.
二.多选题(共4小题)
(多选)6.(2025 江西模拟)关于下列命题,说法正确的是( )
A.若f(x)为奇函数,则f(0)=0
B.“x≥1”是“x2≥x”的充分不必要条件
C.命题p: x∈R,x2﹣2024x+2026>0,则命题p的否定为 x∈R,x2﹣2024x+2026≤0
D.已知数据87,72,75,85,87,90,75,78,86,79,则这组数据的40%分位数是78
【考点】百分位数;充分不必要条件的应用;求存在量词命题的否定;奇函数偶函数的性质.
【专题】对应思想;综合法;函数的性质及应用;简易逻辑;运算求解.
【答案】BC
【分析】举例说明A错误;由充分必要条件的判定判断B;写出命题的否定判定C;由百分位数的定义判断D.
【解答】解:f(x)是奇函数,但f(0)≠0,故A错误;
由x2≥x,得x(x﹣1)≥0,解得x≤0或x≥1,所以“x≥1”是“x2≥x”的充分不必要条件,故B正确;
命题p: x∈R,x2﹣2024x+2026>0,则命题p的否定为 x∈R,x2﹣2024x+2026≤0,故C正确;
将数据从小到大排序为72,75,75,78,79,85,86,87,87,90,
因为10×40%=4,则这组数据的40%分位数是第4个数与第5个数的平均数,即,故D错误.
故选:BC.
【点评】本题考查函数的性质、简易逻辑及百分位数的求法,是基础题.
(多选)7.(2024秋 抚州期末)下列说法正确的是( )
A.数据12,13,14,15,17,19,23,24,27,30的65%分位数是23
B.若样本数据x1,x2,…,x10的方差为8,则数据2x1﹣1,2x2﹣1,…,2x10﹣1的方差为16
C.函数f(x+1)的定义域为[0,1],则f(3x)的定义域为[3,9]
D.若2a=3b=12,则的值为1
【考点】百分位数;方差.
【专题】函数思想;综合法;函数的性质及应用;概率与统计;运算求解.
【答案】AD
【分析】利用百分位数的定义可判断A,利用方差的性质可判断B,利用函数定义域的定义可判断C,利用指数式与对数式的互化,以及对数的运算性质可判断D.
【解答】解:对于A,因为10×65%=6.5,
所以数据12,13,14,15,17,19,23,24,27,30的65%分位数是23,故A正确;
对于B,若样本数据x1,x2,…,x10的方差为8,
则数据2x1﹣1,2x2﹣1,…,2x10﹣1的方差为22×8=32,故B错误;
对于C,因为函数f(x+1)的定义域为[0,1],
所以1≤x+1≤2,
所以1≤3x≤2,
解得0≤x≤log32,
所以f(3x)的定义域为[0,log32],故C错误;
对于D,若2a=3b=12,则a=log212,b=log312,
所以2log122+log123=log124+log123=log1212=1,故D正确.
故选:AD.
【点评】本题主要考查了百分位数的定义,考查了方差的性质,以及对数的运算性质,属于基础题.
(多选)8.(2024秋 汉中期末)午子山景区,又称“午子山风景名胜区”,简称“午子山”,亦名“武子山”或“母子山”,是国家AAAA级旅游景区,位于陕西省汉中市西乡县堰口镇堰口社区,总面积约27平方千米,始建于西汉.午子山景区是集自然山水风光、珍稀植物、茶园、果园、田园风光、堰上古镇、宗教文化活动等于一体的旅游风景名胜区,为道教活动圣地和陕南道教活动中心,素有“汉南胜景区、陕南小华山、陕南小武当”之美称,是观光旅游、宗教朝拜的圣地.为更好地提升旅游品质,午子山景区的工作人员随机选择100名游客对景区进行满意度评分,根据评分,制成如图所示的频率分布直方图.判断下列说法正确的是( )
A.x=0.030
B.工作人员所选取的100人中在[80,90)的人数为3人
C.工作人员采用按分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,则在[50,60)中抽取2人,在[60,70)中抽取4人
D.按分层抽样的方法从评分在[50,60),[60,70)的两组中抽取的6人中再抽两人,则选取的2人评分分别在[50,60)和[60,70)内各1人的概率为
【考点】频率分布直方图的应用.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】ACD
【分析】根据频率分布直方图的性质,分层抽样的概念,古典概型的概率公式,即可分别求解.
【解答】解:根据题意可得(0.005+0.01+0.015+x+0.04)×10=1,解得x=0.030,所以A选项正确;
因为[80,90)的频率为0.3,所以工作人员所选取的100人中在[80,90)的人数为30人,
所以B选项错误;
因为[50,60),[60,70)的两组的频率之比为0.05:0.1=2:4,
所以工作人员采用按分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,
则在[50,60)中抽取2人,在[60,70)中抽取4人,所以C选项正确;
因为在[50,60)中抽取2人,在[60,70)中抽取4人,
所以再抽从这6人中抽2人,则选取的2人评分分别在[50,60)和[60,70)内各1人的概率为,所以D选项正确.
故选:ACD.
【点评】本题考查频率分布直方图的综合应用,属中档题.
(多选)9.(2024秋 汉中期末)某校开展了以“奋进新征程,强国伴我行”为主题的知识竞赛,其中高一年级选派了10名同学参赛,且这10名同学的成绩(单位:分)依次是85,77,92,88,95,88,93,92,96,84,则下列说法不正确的是( )
A.这10名同学成绩的平均数为89分,方差为3.06
B.这10名同学成绩的中位数为92分,众数为88分和92分
C.这10名同学成绩的极差为18分
D.这10名同学成绩的75%分位数为93分
【考点】中位数;众数;极差;百分位数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】ABCD
【分析】利用平均数、方差的定义判断A;利用中位数、众数判断B;利用极差的定义判断C;利用百分位数的定义判断D.
【解答】解:高一年级选派了10名同学参赛,且这10名同学的成绩(单位:分)依次是85,77,92,88,95,88,93,92,96,84,
这组数据从小到大为77,84,85,88,88,92,92,93,95,96,
这组数据的平均数为:
(77+84+85+88+88+92+92+93+95+96)=89分,
方差为:S2[(77﹣89)2+(84﹣89)2+(85﹣89)2+(88﹣89)2+(88﹣89)2+(92﹣89)2+(92﹣89)2+(93﹣89)2+(95﹣89)2+(96﹣89)2]=30.6,故A错误;
这10名同学成绩的中位数为88分,众数为88分和92分,故B错误;
这10名学生的极差为96﹣77=19分,故C错误;
10×75%=7.5,
∴这10名同学成绩的75%分位数为92分,故D错误.
故选:ABCD.
【点评】本题考查平均数、方差、中位数、众数、极差、百分位数等基础知识,考查运算求解能力,是基础题.
三.填空题(共3小题)
10.(2024秋 牡丹江期末)若样本数据x1,x2,x3,x4,x5的平均数为2,则数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3的平均数为 7 .
【考点】平均数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】7.
【分析】根据平均数的性质计算可得.
【解答】解:样本数据x1,x2,x3,x4,x5的平均数为2,
则由平均数的定义和性质得:
数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3的平均数为:
2×2+3=7.
即数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3的平均数为7.
故答案为:7.
【点评】本题考查平均数等基础知识,考查运算求解能力,是基础题.
11.(2024秋 抚州期末)抚州市政府为了促进十一黄金假期期间文昌里文化街区餐饮服务质量的提升,抚州市旅游管理部门需了解游客对餐饮服务工作的认可程度.为此该部门随机调查了500名游客,把这500名游客对餐饮服务工作认可程度给出的评分分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示的频率分布直方图.则直方图中x的值为 0.010 ,评分的平均数为 79.5 .
【考点】频率分布直方图的应用.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】0.010;79.5.
【分析】根据频率分布直方图的性质及平均数的概念,即可求解.
【解答】解:根据题意可得(x+0.015+0.02+0.03+0.025)×10=1,解得x=0.010;
估计评分的平均数为55×0.1+65×0.15+75×0.2+85×0.3+95×0.25=79.5.
故答案为:0.010;79.5.
【点评】本题考查频率分布直方图的性质及应用,属中档题.
12.(2024秋 徐汇区校级期末)若样本数据x1,x2, ,x10的方差为16,则数据1﹣2x1,1﹣2x2,1﹣2x10的标准差为 8 .
【考点】方差;标准差.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】8.
【分析】设样本数据x1,x2, ,x10的方差为S2,则数据1﹣2x1,1﹣2x2,1﹣2x10的方差为4S2,即可得到标准差.
【解答】解:样本数据x1,x2, ,x10的方差为16,
设样本数据x1,x2, ,x10的方差为S2,则S2=16,
可知数据1﹣2x1,1﹣2x2,1﹣2x10的方差为4S2=64,
∴数据1﹣2x1,1﹣2x2,1﹣2x10的标准差为8.
故答案为:8.
【点评】本题考查方差的性质及运算等基础知识,考查运算求解能力,是基础题.
四.解答题(共3小题)
13.(2024秋 浦东新区校级期末)某学校组织全校学生进行了一次“两会知识知多少”的问卷测试,已知所有学生的测试成绩均位于区间[50,100],从中随机抽取了40名学生的测试成绩,绘制得到如图所示的频率分布直方图.
(1)求图中a的值,并估算这40名学生测试成绩的平均数;
(2)现学校准备利用分层随机抽样方法,从[80,90)和[90,100]的学生中抽取7人组成两会知识宣讲团.从选定的7人中随机抽取2人对高一同学进行宣讲,设事件A为“至少有1人测试成绩位于区间[90,100]”,求事件A发生的概率.
【考点】频率分布直方图的应用.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】(1)a=0.030;74.5;
(2).
【分析】(1)根据频率分布直方图中所有小矩形的面积之和等于1列方程,可得实数a的值,进而求平均数;
(2)根据频率分布直方图得比例抽样,列出7人中随机抽取2人的21种情况,确定至少有1人测试成绩位于区间[90,100]有11种,即可得解.
【解答】解:(1)根据题意可得(0.015+0.020+a+0.025+0.010)×10=1,解得a=0.030,
所以这40名学生测试成绩的平均数为55×0.15+65×0.2+75×0.3+85×0.25+95×0.1=74.5;
(2)因为80,90]和[90,100]这两组的频率之比为0.25:0.1=5:2,
所以在[80,90]中抽5人,在[90,100]中抽2人,
设从[80,90]学生中抽取的5人为a,b,c,d,e,从[90,100]学生中抽取的2人为1,2,
则这个试验的样本空间为Ω={ab,ac,ad,ae,a1,a2,bc,bd,be,b1,b2,cd,ce,c1,c2,de,d1,d2,e1,e2,12},
故n(Ω)=21,
又A={a1,a2,b1,b2,c1,c2,d1,d2,e1,e2,12},则n(A)=11,
所以事件A的概率为.
【点评】本题考查频率分布直方图的综合应用,属中档题.
14.(2024秋 徐汇区校级期末)某工厂选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:分钟)绘制了如下茎叶图:
(1)求40名工人完成生产任务所需时间的第75百分数;
(2)为了解该工厂职工的基本信息,从工厂中抽取了100个职工的体重数据,发现全部介于45公斤到75公斤之间,现将100个体重数据分为6组:第一组[45,50),第二组[50,55),…,第六组[70,75),得到如图2所示的频率分布直方图.其中第一组有2人,第二组有13人.求与a的值.
【考点】频率分布直方图的应用;百分位数.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】(1)88.5;
(2).
【分析】(1)按照求百分数的计算步骤计算即可;
(2)据直方图面积为1的性质及第一组第二组的人数建立方程组,解出a,b,c,进而得解.
【解答】解:(1)因为40名工人完成生产任务所需时间按从小到大排列为:
61,61,62,63,63,65,65,67,68,69,70,70,71,72,72,72,72,74,75,77,
78,81,82,82,83,84,84,84,87,87,90,90,91,91,91,92,92,93,94,94,
又40×75%=30,所以第75百分数为;
(2)根据题意可得(2a+2b+2c)×5=1,5a×100=2,5b×100=13,
解得a=0.004,b=0.026,c=0.07,
所以.
【点评】本题考查频率分布直方图的综合应用,属中档题.
15.(2024秋 雷州市校级期末)为激发户外运动爱好者健身热情,增进群众健身获得感、幸福感.某市体育部门随机抽取200名群众进行每天体育运动时间的调查,按照时长(单位:分钟)分成6组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90].处理后绘制了如下图的频率分布直方图.
(1)求图中a的值;
(2)求运动时长在[50,70)的样本群众人数;
(3)估计该市群众每天体育运动时间的众数、平均数、中位数(保留1位小数).
【考点】频率分布直方图的应用.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】(1)a=0.015;
(2)90;
(3)众数为55,平均数58.5,中位数为56.7.
【分析】(1)根据频率和为1计算求参即可;
(2)先求出[50,70)的频率再计算频数即可;
(3)应用频率分布图计算众数,平均数及中位数定义分别计算求解即可.
【解答】解:(1)根据题意可得(0.01+0.02+0.03+2a+0.01)×10=1,解得a=0.015;
(2)因为[50,70)的频率为(0.03+0.015)×10=0.45,
所以运动时长为[50,70)的样本群众人数为200×0.45=90;
(3)根据题意可得该市群众每天体育运动时间的众数约为;
该市群众每天体育运动时间的平均数约为:
0.01×10×35+0.02×10×45+0.03×10×55+0.015×10×65+0.015×10×75+0.01×10×85=58.5;
因为前几组的频率依次为0.1,0.2,0.3,
所以中位数在50和60之间,设为x,则0.3+(x﹣50)×0.03=0.5,解得x=56.7,
即该市群众每天体育运动时间的中位数约为56.7.
【点评】本题考查频率分布直方图的综合应用,属中档题。
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 辽宁期末)某地有9个快递收件点,在某天接收的快递个数分别为361,285,293,305,403,189,247,265,289,则这组数据的第72百分位数为( )
A.289 B.299 C.305 D.361
2.(2024秋 喀什市期末)已知一组数据3,7,11,7,13,15,则该组数据的第40百分位数为( )
A.7 B.9 C.11 D.12
3.(2025 聊城校级模拟)利用微信转账余额提醒这一小程序从数据库中得到某人一天内的网上交易额如下:26,32,7,13,42,114,则该组数据的平均数为( )
A.36 B.39 C.40 D.41
4.(2025 福建模拟)市环保局开展了环境治理专项活动,活动结束后对志愿者做了一次随机抽样调查,统计整理了部分志愿者的服务时长(单位:小时),得到如图所示的频率分布直方图,据此估计志愿者服务时长的第90百分位数为( )
A.36 B.37 C.38 D.39
5.(2025 温州模拟)已知4名学生的期中考试数学成绩分别为98,110,m,120,且上四分位数为118,则m=( )
A.115 B.116 C.117 D.118
二.多选题(共4小题)
(多选)6.(2025 江西模拟)关于下列命题,说法正确的是( )
A.若f(x)为奇函数,则f(0)=0
B.“x≥1”是“x2≥x”的充分不必要条件
C.命题p: x∈R,x2﹣2024x+2026>0,则命题p的否定为 x∈R,x2﹣2024x+2026≤0
D.已知数据87,72,75,85,87,90,75,78,86,79,则这组数据的40%分位数是78
(多选)7.(2024秋 抚州期末)下列说法正确的是( )
A.数据12,13,14,15,17,19,23,24,27,30的65%分位数是23
B.若样本数据x1,x2,…,x10的方差为8,则数据2x1﹣1,2x2﹣1,…,2x10﹣1的方差为16
C.函数f(x+1)的定义域为[0,1],则f(3x)的定义域为[3,9]
D.若2a=3b=12,则的值为1
(多选)8.(2024秋 汉中期末)午子山景区,又称“午子山风景名胜区”,简称“午子山”,亦名“武子山”或“母子山”,是国家AAAA级旅游景区,位于陕西省汉中市西乡县堰口镇堰口社区,总面积约27平方千米,始建于西汉.午子山景区是集自然山水风光、珍稀植物、茶园、果园、田园风光、堰上古镇、宗教文化活动等于一体的旅游风景名胜区,为道教活动圣地和陕南道教活动中心,素有“汉南胜景区、陕南小华山、陕南小武当”之美称,是观光旅游、宗教朝拜的圣地.为更好地提升旅游品质,午子山景区的工作人员随机选择100名游客对景区进行满意度评分,根据评分,制成如图所示的频率分布直方图.判断下列说法正确的是( )
A.x=0.030
B.工作人员所选取的100人中在[80,90)的人数为3人
C.工作人员采用按分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,则在[50,60)中抽取2人,在[60,70)中抽取4人
D.按分层抽样的方法从评分在[50,60),[60,70)的两组中抽取的6人中再抽两人,则选取的2人评分分别在[50,60)和[60,70)内各1人的概率为
(多选)9.(2024秋 汉中期末)某校开展了以“奋进新征程,强国伴我行”为主题的知识竞赛,其中高一年级选派了10名同学参赛,且这10名同学的成绩(单位:分)依次是85,77,92,88,95,88,93,92,96,84,则下列说法不正确的是( )
A.这10名同学成绩的平均数为89分,方差为3.06
B.这10名同学成绩的中位数为92分,众数为88分和92分
C.这10名同学成绩的极差为18分
D.这10名同学成绩的75%分位数为93分
三.填空题(共3小题)
10.(2024秋 牡丹江期末)若样本数据x1,x2,x3,x4,x5的平均数为2,则数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3的平均数为 .
11.(2024秋 抚州期末)抚州市政府为了促进十一黄金假期期间文昌里文化街区餐饮服务质量的提升,抚州市旅游管理部门需了解游客对餐饮服务工作的认可程度.为此该部门随机调查了500名游客,把这500名游客对餐饮服务工作认可程度给出的评分分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示的频率分布直方图.则直方图中x的值为 ,评分的平均数为 .
12.(2024秋 徐汇区校级期末)若样本数据x1,x2, ,x10的方差为16,则数据1﹣2x1,1﹣2x2,1﹣2x10的标准差为 .
四.解答题(共3小题)
13.(2024秋 浦东新区校级期末)某学校组织全校学生进行了一次“两会知识知多少”的问卷测试,已知所有学生的测试成绩均位于区间[50,100],从中随机抽取了40名学生的测试成绩,绘制得到如图所示的频率分布直方图.
(1)求图中a的值,并估算这40名学生测试成绩的平均数;
(2)现学校准备利用分层随机抽样方法,从[80,90)和[90,100]的学生中抽取7人组成两会知识宣讲团.从选定的7人中随机抽取2人对高一同学进行宣讲,设事件A为“至少有1人测试成绩位于区间[90,100]”,求事件A发生的概率.
14.(2024秋 徐汇区校级期末)某工厂选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:分钟)绘制了如下茎叶图:
(1)求40名工人完成生产任务所需时间的第75百分数;
(2)为了解该工厂职工的基本信息,从工厂中抽取了100个职工的体重数据,发现全部介于45公斤到75公斤之间,现将100个体重数据分为6组:第一组[45,50),第二组[50,55),…,第六组[70,75),得到如图2所示的频率分布直方图.其中第一组有2人,第二组有13人.求与a的值.
15.(2024秋 雷州市校级期末)为激发户外运动爱好者健身热情,增进群众健身获得感、幸福感.某市体育部门随机抽取200名群众进行每天体育运动时间的调查,按照时长(单位:分钟)分成6组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90].处理后绘制了如下图的频率分布直方图.
(1)求图中a的值;
(2)求运动时长在[50,70)的样本群众人数;
(3)估计该市群众每天体育运动时间的众数、平均数、中位数(保留1位小数).
期末热点.重难点 用样本估计总体
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 辽宁期末)某地有9个快递收件点,在某天接收的快递个数分别为361,285,293,305,403,189,247,265,289,则这组数据的第72百分位数为( )
A.289 B.299 C.305 D.361
【考点】百分位数.
【专题】转化思想;分析法;概率与统计;运算求解.
【答案】C
【分析】根据百分位数的估计方法计算即可.
【解答】解:将这组数据361,285,293,305,403,189,247,265,289,
按照从小到大的顺序排列得189,247,265,285,289,293,305,361,403,
因为9×0.72=6.48,所以这组数据的第72百分位数为第7个数305.
故选:C.
【点评】本题考查百分位数的定义,是基础题.
2.(2024秋 喀什市期末)已知一组数据3,7,11,7,13,15,则该组数据的第40百分位数为( )
A.7 B.9 C.11 D.12
【考点】百分位数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】A
【分析】根据百分位数的定义直接计算.
【解答】解:一组数据3,7,11,7,13,15,
将数据从小到大排列得到:3,7,7,11,13,15,
∵6×0.4=2.4,
∴这组数据的第40百分位数为第三个数据7.
故选:A.
【点评】本题考查百分位数的定义等基础知识,考查运算求解能力,是基础题.
3.(2025 聊城校级模拟)利用微信转账余额提醒这一小程序从数据库中得到某人一天内的网上交易额如下:26,32,7,13,42,114,则该组数据的平均数为( )
A.36 B.39 C.40 D.41
【考点】平均数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】B
【分析】利用平均数的计算公式直接计算即可.
【解答】解:根据平均数的定义可得,该组数据的平均数为39.
故选:B.
【点评】本题考查平均数的应用,属于基础题.
4.(2025 福建模拟)市环保局开展了环境治理专项活动,活动结束后对志愿者做了一次随机抽样调查,统计整理了部分志愿者的服务时长(单位:小时),得到如图所示的频率分布直方图,据此估计志愿者服务时长的第90百分位数为( )
A.36 B.37 C.38 D.39
【考点】百分位数.
【专题】数形结合;数形结合法;概率与统计;运算求解.
【答案】C
【分析】利用频率分布直方图的性质求出a的值,再结合第90百分位数定义求解即可.
【解答】解:由题意得组距为24﹣20=4,
∵小长方形面积和为1,∴4×(0.005+0.065+0.040+0.090+a)=1,
解得a=0.050,
∵4×(0.005+0.065+0.040+0.090)=0.8,
∴第90百分位数在[36,40]内,
设第90百分位数为x,
得到0.8+0.05(x﹣36)=0.9,解得x=38.
故选:C.
【点评】本题考查频率分布直方图的性质、百分位数等基础知识,考查运算求解能力,是基础题.
5.(2025 温州模拟)已知4名学生的期中考试数学成绩分别为98,110,m,120,且上四分位数为118,则m=( )
A.115 B.116 C.117 D.118
【考点】百分位数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】B
【分析】利用百分位数定义求解.
【解答】解:4名学生的期中考试数学成绩分别为98,110,m,120,且上四分位数为118,
4×75%=3是整数,∴,得m=116.
故选:B.
【点评】本题考查百分位数定义等基础知识,考查运算求解能力,是基础题.
二.多选题(共4小题)
(多选)6.(2025 江西模拟)关于下列命题,说法正确的是( )
A.若f(x)为奇函数,则f(0)=0
B.“x≥1”是“x2≥x”的充分不必要条件
C.命题p: x∈R,x2﹣2024x+2026>0,则命题p的否定为 x∈R,x2﹣2024x+2026≤0
D.已知数据87,72,75,85,87,90,75,78,86,79,则这组数据的40%分位数是78
【考点】百分位数;充分不必要条件的应用;求存在量词命题的否定;奇函数偶函数的性质.
【专题】对应思想;综合法;函数的性质及应用;简易逻辑;运算求解.
【答案】BC
【分析】举例说明A错误;由充分必要条件的判定判断B;写出命题的否定判定C;由百分位数的定义判断D.
【解答】解:f(x)是奇函数,但f(0)≠0,故A错误;
由x2≥x,得x(x﹣1)≥0,解得x≤0或x≥1,所以“x≥1”是“x2≥x”的充分不必要条件,故B正确;
命题p: x∈R,x2﹣2024x+2026>0,则命题p的否定为 x∈R,x2﹣2024x+2026≤0,故C正确;
将数据从小到大排序为72,75,75,78,79,85,86,87,87,90,
因为10×40%=4,则这组数据的40%分位数是第4个数与第5个数的平均数,即,故D错误.
故选:BC.
【点评】本题考查函数的性质、简易逻辑及百分位数的求法,是基础题.
(多选)7.(2024秋 抚州期末)下列说法正确的是( )
A.数据12,13,14,15,17,19,23,24,27,30的65%分位数是23
B.若样本数据x1,x2,…,x10的方差为8,则数据2x1﹣1,2x2﹣1,…,2x10﹣1的方差为16
C.函数f(x+1)的定义域为[0,1],则f(3x)的定义域为[3,9]
D.若2a=3b=12,则的值为1
【考点】百分位数;方差.
【专题】函数思想;综合法;函数的性质及应用;概率与统计;运算求解.
【答案】AD
【分析】利用百分位数的定义可判断A,利用方差的性质可判断B,利用函数定义域的定义可判断C,利用指数式与对数式的互化,以及对数的运算性质可判断D.
【解答】解:对于A,因为10×65%=6.5,
所以数据12,13,14,15,17,19,23,24,27,30的65%分位数是23,故A正确;
对于B,若样本数据x1,x2,…,x10的方差为8,
则数据2x1﹣1,2x2﹣1,…,2x10﹣1的方差为22×8=32,故B错误;
对于C,因为函数f(x+1)的定义域为[0,1],
所以1≤x+1≤2,
所以1≤3x≤2,
解得0≤x≤log32,
所以f(3x)的定义域为[0,log32],故C错误;
对于D,若2a=3b=12,则a=log212,b=log312,
所以2log122+log123=log124+log123=log1212=1,故D正确.
故选:AD.
【点评】本题主要考查了百分位数的定义,考查了方差的性质,以及对数的运算性质,属于基础题.
(多选)8.(2024秋 汉中期末)午子山景区,又称“午子山风景名胜区”,简称“午子山”,亦名“武子山”或“母子山”,是国家AAAA级旅游景区,位于陕西省汉中市西乡县堰口镇堰口社区,总面积约27平方千米,始建于西汉.午子山景区是集自然山水风光、珍稀植物、茶园、果园、田园风光、堰上古镇、宗教文化活动等于一体的旅游风景名胜区,为道教活动圣地和陕南道教活动中心,素有“汉南胜景区、陕南小华山、陕南小武当”之美称,是观光旅游、宗教朝拜的圣地.为更好地提升旅游品质,午子山景区的工作人员随机选择100名游客对景区进行满意度评分,根据评分,制成如图所示的频率分布直方图.判断下列说法正确的是( )
A.x=0.030
B.工作人员所选取的100人中在[80,90)的人数为3人
C.工作人员采用按分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,则在[50,60)中抽取2人,在[60,70)中抽取4人
D.按分层抽样的方法从评分在[50,60),[60,70)的两组中抽取的6人中再抽两人,则选取的2人评分分别在[50,60)和[60,70)内各1人的概率为
【考点】频率分布直方图的应用.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】ACD
【分析】根据频率分布直方图的性质,分层抽样的概念,古典概型的概率公式,即可分别求解.
【解答】解:根据题意可得(0.005+0.01+0.015+x+0.04)×10=1,解得x=0.030,所以A选项正确;
因为[80,90)的频率为0.3,所以工作人员所选取的100人中在[80,90)的人数为30人,
所以B选项错误;
因为[50,60),[60,70)的两组的频率之比为0.05:0.1=2:4,
所以工作人员采用按分层抽样的方法从评分在[50,60),[60,70)的两组中共抽取6人,
则在[50,60)中抽取2人,在[60,70)中抽取4人,所以C选项正确;
因为在[50,60)中抽取2人,在[60,70)中抽取4人,
所以再抽从这6人中抽2人,则选取的2人评分分别在[50,60)和[60,70)内各1人的概率为,所以D选项正确.
故选:ACD.
【点评】本题考查频率分布直方图的综合应用,属中档题.
(多选)9.(2024秋 汉中期末)某校开展了以“奋进新征程,强国伴我行”为主题的知识竞赛,其中高一年级选派了10名同学参赛,且这10名同学的成绩(单位:分)依次是85,77,92,88,95,88,93,92,96,84,则下列说法不正确的是( )
A.这10名同学成绩的平均数为89分,方差为3.06
B.这10名同学成绩的中位数为92分,众数为88分和92分
C.这10名同学成绩的极差为18分
D.这10名同学成绩的75%分位数为93分
【考点】中位数;众数;极差;百分位数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】ABCD
【分析】利用平均数、方差的定义判断A;利用中位数、众数判断B;利用极差的定义判断C;利用百分位数的定义判断D.
【解答】解:高一年级选派了10名同学参赛,且这10名同学的成绩(单位:分)依次是85,77,92,88,95,88,93,92,96,84,
这组数据从小到大为77,84,85,88,88,92,92,93,95,96,
这组数据的平均数为:
(77+84+85+88+88+92+92+93+95+96)=89分,
方差为:S2[(77﹣89)2+(84﹣89)2+(85﹣89)2+(88﹣89)2+(88﹣89)2+(92﹣89)2+(92﹣89)2+(93﹣89)2+(95﹣89)2+(96﹣89)2]=30.6,故A错误;
这10名同学成绩的中位数为88分,众数为88分和92分,故B错误;
这10名学生的极差为96﹣77=19分,故C错误;
10×75%=7.5,
∴这10名同学成绩的75%分位数为92分,故D错误.
故选:ABCD.
【点评】本题考查平均数、方差、中位数、众数、极差、百分位数等基础知识,考查运算求解能力,是基础题.
三.填空题(共3小题)
10.(2024秋 牡丹江期末)若样本数据x1,x2,x3,x4,x5的平均数为2,则数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3的平均数为 7 .
【考点】平均数.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】7.
【分析】根据平均数的性质计算可得.
【解答】解:样本数据x1,x2,x3,x4,x5的平均数为2,
则由平均数的定义和性质得:
数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3的平均数为:
2×2+3=7.
即数据2x1+3,2x2+3,2x3+3,2x4+3,2x5+3的平均数为7.
故答案为:7.
【点评】本题考查平均数等基础知识,考查运算求解能力,是基础题.
11.(2024秋 抚州期末)抚州市政府为了促进十一黄金假期期间文昌里文化街区餐饮服务质量的提升,抚州市旅游管理部门需了解游客对餐饮服务工作的认可程度.为此该部门随机调查了500名游客,把这500名游客对餐饮服务工作认可程度给出的评分分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示的频率分布直方图.则直方图中x的值为 0.010 ,评分的平均数为 79.5 .
【考点】频率分布直方图的应用.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】0.010;79.5.
【分析】根据频率分布直方图的性质及平均数的概念,即可求解.
【解答】解:根据题意可得(x+0.015+0.02+0.03+0.025)×10=1,解得x=0.010;
估计评分的平均数为55×0.1+65×0.15+75×0.2+85×0.3+95×0.25=79.5.
故答案为:0.010;79.5.
【点评】本题考查频率分布直方图的性质及应用,属中档题.
12.(2024秋 徐汇区校级期末)若样本数据x1,x2, ,x10的方差为16,则数据1﹣2x1,1﹣2x2,1﹣2x10的标准差为 8 .
【考点】方差;标准差.
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】8.
【分析】设样本数据x1,x2, ,x10的方差为S2,则数据1﹣2x1,1﹣2x2,1﹣2x10的方差为4S2,即可得到标准差.
【解答】解:样本数据x1,x2, ,x10的方差为16,
设样本数据x1,x2, ,x10的方差为S2,则S2=16,
可知数据1﹣2x1,1﹣2x2,1﹣2x10的方差为4S2=64,
∴数据1﹣2x1,1﹣2x2,1﹣2x10的标准差为8.
故答案为:8.
【点评】本题考查方差的性质及运算等基础知识,考查运算求解能力,是基础题.
四.解答题(共3小题)
13.(2024秋 浦东新区校级期末)某学校组织全校学生进行了一次“两会知识知多少”的问卷测试,已知所有学生的测试成绩均位于区间[50,100],从中随机抽取了40名学生的测试成绩,绘制得到如图所示的频率分布直方图.
(1)求图中a的值,并估算这40名学生测试成绩的平均数;
(2)现学校准备利用分层随机抽样方法,从[80,90)和[90,100]的学生中抽取7人组成两会知识宣讲团.从选定的7人中随机抽取2人对高一同学进行宣讲,设事件A为“至少有1人测试成绩位于区间[90,100]”,求事件A发生的概率.
【考点】频率分布直方图的应用.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】(1)a=0.030;74.5;
(2).
【分析】(1)根据频率分布直方图中所有小矩形的面积之和等于1列方程,可得实数a的值,进而求平均数;
(2)根据频率分布直方图得比例抽样,列出7人中随机抽取2人的21种情况,确定至少有1人测试成绩位于区间[90,100]有11种,即可得解.
【解答】解:(1)根据题意可得(0.015+0.020+a+0.025+0.010)×10=1,解得a=0.030,
所以这40名学生测试成绩的平均数为55×0.15+65×0.2+75×0.3+85×0.25+95×0.1=74.5;
(2)因为80,90]和[90,100]这两组的频率之比为0.25:0.1=5:2,
所以在[80,90]中抽5人,在[90,100]中抽2人,
设从[80,90]学生中抽取的5人为a,b,c,d,e,从[90,100]学生中抽取的2人为1,2,
则这个试验的样本空间为Ω={ab,ac,ad,ae,a1,a2,bc,bd,be,b1,b2,cd,ce,c1,c2,de,d1,d2,e1,e2,12},
故n(Ω)=21,
又A={a1,a2,b1,b2,c1,c2,d1,d2,e1,e2,12},则n(A)=11,
所以事件A的概率为.
【点评】本题考查频率分布直方图的综合应用,属中档题.
14.(2024秋 徐汇区校级期末)某工厂选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:分钟)绘制了如下茎叶图:
(1)求40名工人完成生产任务所需时间的第75百分数;
(2)为了解该工厂职工的基本信息,从工厂中抽取了100个职工的体重数据,发现全部介于45公斤到75公斤之间,现将100个体重数据分为6组:第一组[45,50),第二组[50,55),…,第六组[70,75),得到如图2所示的频率分布直方图.其中第一组有2人,第二组有13人.求与a的值.
【考点】频率分布直方图的应用;百分位数.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】(1)88.5;
(2).
【分析】(1)按照求百分数的计算步骤计算即可;
(2)据直方图面积为1的性质及第一组第二组的人数建立方程组,解出a,b,c,进而得解.
【解答】解:(1)因为40名工人完成生产任务所需时间按从小到大排列为:
61,61,62,63,63,65,65,67,68,69,70,70,71,72,72,72,72,74,75,77,
78,81,82,82,83,84,84,84,87,87,90,90,91,91,91,92,92,93,94,94,
又40×75%=30,所以第75百分数为;
(2)根据题意可得(2a+2b+2c)×5=1,5a×100=2,5b×100=13,
解得a=0.004,b=0.026,c=0.07,
所以.
【点评】本题考查频率分布直方图的综合应用,属中档题.
15.(2024秋 雷州市校级期末)为激发户外运动爱好者健身热情,增进群众健身获得感、幸福感.某市体育部门随机抽取200名群众进行每天体育运动时间的调查,按照时长(单位:分钟)分成6组:[30,40),[40,50),[50,60),[60,70),[70,80),[80,90].处理后绘制了如下图的频率分布直方图.
(1)求图中a的值;
(2)求运动时长在[50,70)的样本群众人数;
(3)估计该市群众每天体育运动时间的众数、平均数、中位数(保留1位小数).
【考点】频率分布直方图的应用.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】(1)a=0.015;
(2)90;
(3)众数为55,平均数58.5,中位数为56.7.
【分析】(1)根据频率和为1计算求参即可;
(2)先求出[50,70)的频率再计算频数即可;
(3)应用频率分布图计算众数,平均数及中位数定义分别计算求解即可.
【解答】解:(1)根据题意可得(0.01+0.02+0.03+2a+0.01)×10=1,解得a=0.015;
(2)因为[50,70)的频率为(0.03+0.015)×10=0.45,
所以运动时长为[50,70)的样本群众人数为200×0.45=90;
(3)根据题意可得该市群众每天体育运动时间的众数约为;
该市群众每天体育运动时间的平均数约为:
0.01×10×35+0.02×10×45+0.03×10×55+0.015×10×65+0.015×10×75+0.01×10×85=58.5;
因为前几组的频率依次为0.1,0.2,0.3,
所以中位数在50和60之间,设为x,则0.3+(x﹣50)×0.03=0.5,解得x=56.7,
即该市群众每天体育运动时间的中位数约为56.7.
【点评】本题考查频率分布直方图的综合应用,属中档题。
21世纪教育网(www.21cnjy.com)
同课章节目录
