2024-2025学年北师大版五年级数学下册期末真题汇编专练04-解决问题2(含答案+解析)
文档属性
| 名称 | 2024-2025学年北师大版五年级数学下册期末真题汇编专练04-解决问题2(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 07:38:18 | ||
图片预览



文档简介
2024-2025学年北师大版五年级数学下册期末真题汇编
专练04-解决问题2
一、解决问题
1.(2024五下·期末)2024 年是澳门回归祖国的 25 周年。淘气和同学在六一游学澳门时,汽车正好经过港珠澳大桥。先用10分钟行驶了全长的,又用25 分钟行驶了全长的一半,最后用5分钟通过了大桥。最后5分钟行驶的路程是大桥全长的几分之几?
2.(2024五下·期末)人体血液在主动脉中的流动速度约为20厘米/秒,在静脉中的流动速度约为主动脉中的,血液在静脉中每秒约流动多少厘来?血液在毛细血管中的流动速度大约只有静脉中的,血液在毛细血管中每秒约流动多少厘来?
3.(2023五下·武功期末)”节约资源从我做起”。实验小学上个月开展了收集空矿泉水瓶的活动。五年级收集了165个,是六年级的,四年级收集的个数是六年级的,实验小学四、六年级各收集了多少个空矿泉水瓶?
4.(2024五下·房山期末)工人师傅用木板制作一个长方体种植箱,种植箱的长、宽、高如下图所示,制作这个种植箱需要多少平方分米木板?
5.(2024五下·奉化期末)一个长方体玻璃缸,长4分米,宽3分米,高3分米,把一块不规则石头浸没在水中,水深2分米,捞出这块石头后,水面下降0.5分米,这块石头的体积是多少?
6.(2024五下·朝阳期末)学完第六单元《分数的加法和减法》,同学们提出了一些问题。
(1)请你以为例回答小阳问题,写一写“先通分,再计算”的道理。
(2)请你举例回答小芳的问题,写清整数加法、小数加法和分数加法计算过程中的相同点。
(3)学完这个单元的内容,你还有哪些好奇的问题想要进行研究呢?请在下面至少写出一个问题。
7.(2024五下·房山期末)学校的种植园种了四种蔬菜。其中种植西红柿、豆角、黄瓜的面积与四种蔬菜种植总面积之间的关系如下表所示。
蔬菜种类 西红柿 胡萝卜 豆角 黄瓜
占四种蔬菜种植总面积的几分之几
哪种蔬菜的种植面积最小?请你结合上面的信息,写出思考过程和结果。
8.(2024五下·朝阳期末)丽丽想制作一个长方体纸盒。他先在一张边长为30厘米的正方形纸上绘制出这个长方体纸盒的展开图(如下图)。然后准备将涂色部分裁掉,借助胶条粘贴成长方体。已知长方体的宽是高的2倍,那么这个长方体的体积是多少立方厘米?
9.(2024五下·东城期末)下面是小红7~12岁每年的身高与同龄女学生达标身高的对比统计表。
7 8 9 10 11 12
达标身高/cm 123 128 135 140 148 153
小红身高/cm 112 120 129 139 148 160
根据表中的数据。完成下面各题。
(1)根据表中的数据,把复式折线统计图补充完整。
(2)小红从 岁到 岁身高增长得很快。
(3)请你预测小红 13 岁时的身高并说明理由。
10.(2024五下·东城期末)修一条路,第一天修了全长的。第二天修了全长的,还剩全长的几分之几没有修?
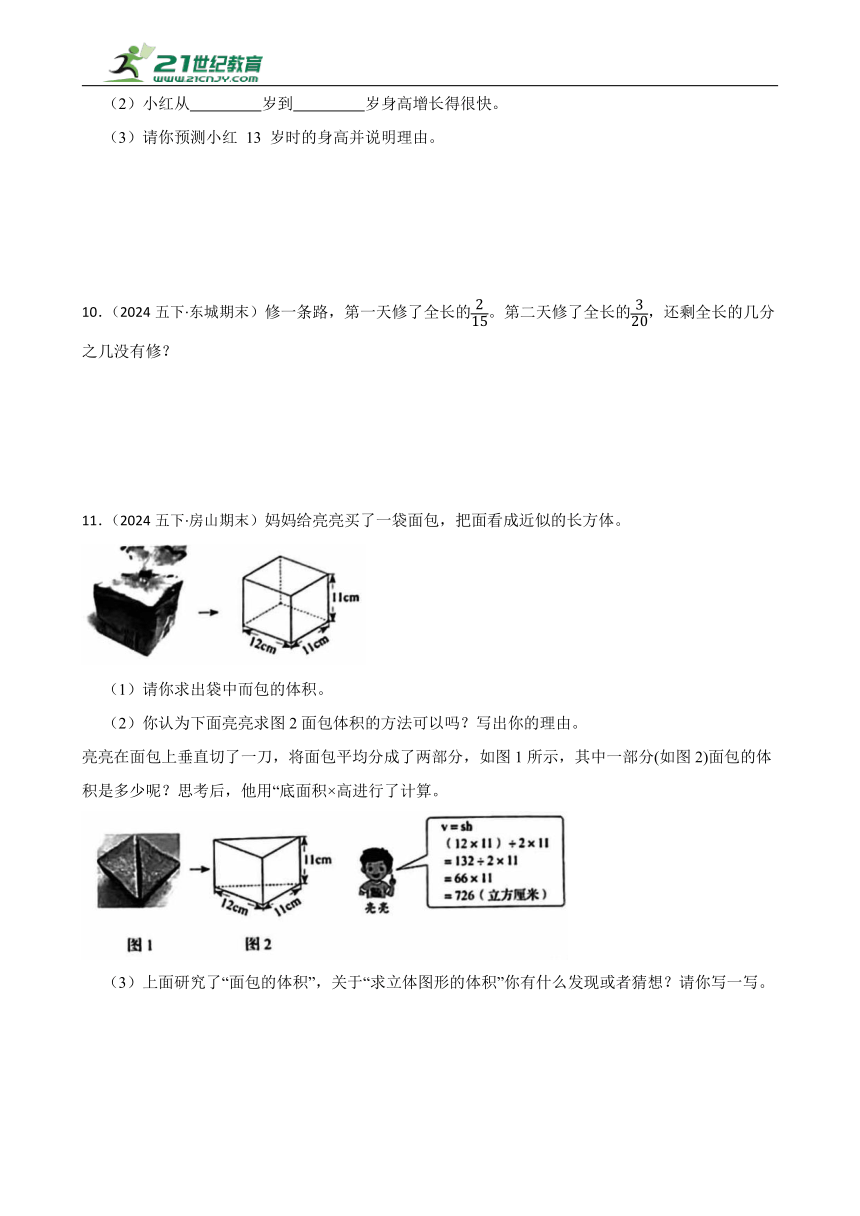
11.(2024五下·房山期末)妈妈给亮亮买了一袋面包,把面看成近似的长方体。
(1)请你求出袋中而包的体积。
(2)你认为下面亮亮求图2面包体积的方法可以吗?写出你的理由。
亮亮在面包上垂直切了一刀,将面包平均分成了两部分,如图1所示,其中一部分(如图2)面包的体积是多少呢?思考后,他用“底面积×高进行了计算。
(3)上面研究了“面包的体积”,关于“求立体图形的体积”你有什么发现或者猜想?请你写一写。
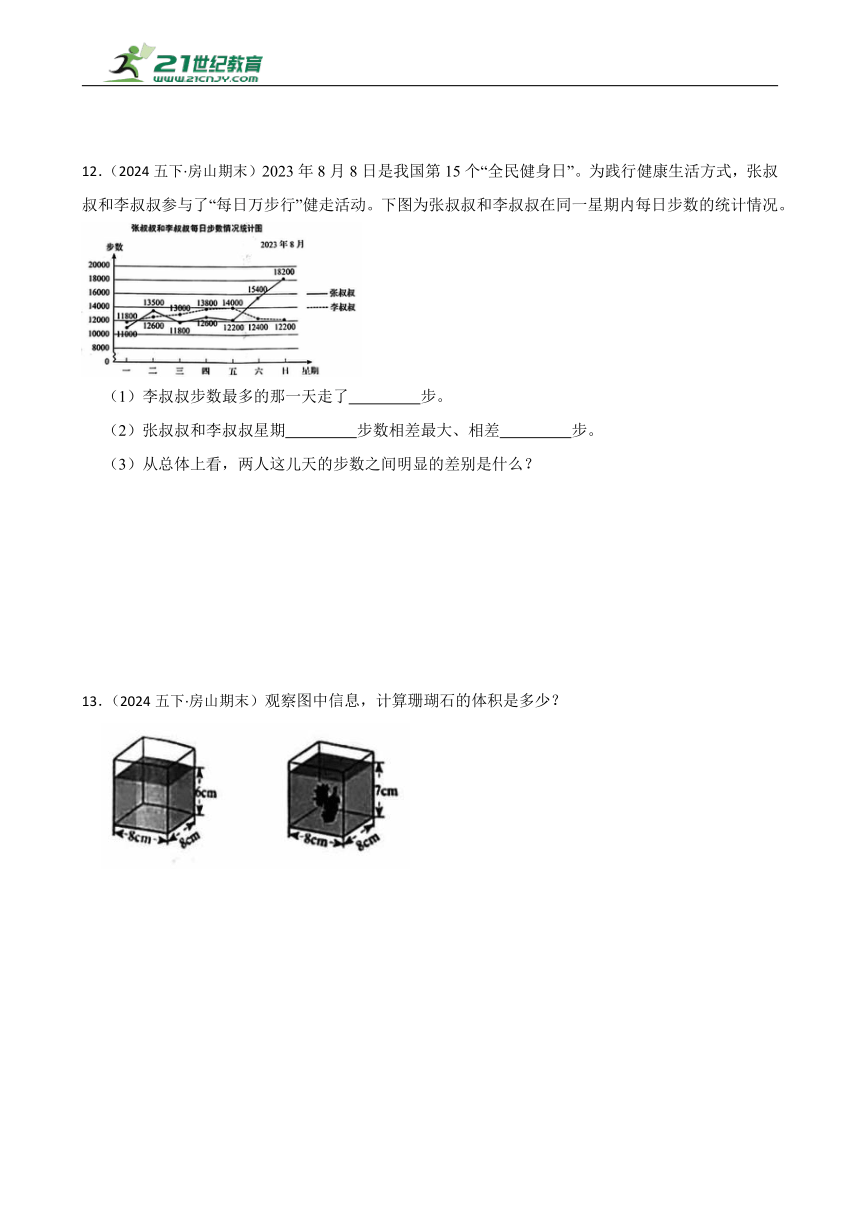
12.(2024五下·房山期末)2023年8月8日是我国第15个“全民健身日”。为践行健康生活方式,张叔叔和李叔叔参与了“每日万步行”健走活动。下图为张叔叔和李叔叔在同一星期内每日步数的统计情况。
(1)李叔叔步数最多的那一天走了 步。
(2)张叔叔和李叔叔星期 步数相差最大、相差 步。
(3)从总体上看,两人这儿天的步数之间明显的差别是什么?
13.(2024五下·房山期末)观察图中信息,计算珊瑚石的体积是多少?
14.(2024五下·朝阳期末)
嫦娥六号着陆器携带的五星红旗在月球表面成功展开。能耐受高真空、高低温循环、强剂量紫外辐照等极端环境的“石头版”高品质织物国旗,是由以玄武岩为主的复合材料制造。嫦娥六号月面展示国旗的大小与嫦娥五号上的国旗规格一样,均为300mm×200mm,与 A4 纸大小相近。
嫦娥六号着陆器携带的国旗重量为克,比嫦娥五号着陆器携带的同规格国旗还要轻克。嫦娥五号着陆器携带的国旗重量是多少克?
15.(2024五下·房山期末)李叔叔用5块铁板制作了一个无盖的长方体水箱,5块铁板的大小如下图所示。这个水箱的容积是多少升?(铁板的厚度忽略不计)
16.(2024五下·房山期末)2022年北京冬季奥运会,中国金牌数首次位居世界三。其中金牌的数量占获得奖牌总数量的,银牌的数量占获得奖牌总数量的。金牌和银牌的数量一共占获得奖牌总数量的儿分之儿?
17.(2024五下·柯桥期末) 星期天, 聪聪从家出发去学校, 行了全程的 到图书馆, 行了全程的 到商店(如图)。
(1)聪聪再行全程的几分之几就能到达学校
(2)从图书馆到商店的路程占全程的几分之几
18.(2024五下·丰台期末)肥胖影响青少年的身心健康。在常规体检中,乐乐和强强的健康状况为“超重”,体检医生提示他们需要加强体育锻炼、注意健康饮食。为此,乐乐和强强每天进行了至少一小时的体育运动,并将一月至五月每天的各类食物摄入量和阶段性的体重监测情况进行了记录,如下面两幅统计图所示:
(1)乐乐和强强每天摄入 类食物相差最多。
(2)乐乐每天肉类的摄入量是强强的 。
(3)请你结合两幅图中的数据判断谁的体重下降的比较快,并分析可能的原因。
19.(2024五下·丰台期末)请你设计一个长方体包装盒,恰好能装下4个探在一起的玻璃杯。为了展示出玻璃杯的样子,前面使用透明塑料膜,其他各面都用纸板。做这个包装盒至少需要多少平方厘米纸板?(纸板厚度和粘接重叠部分忽略不计)
20.(2024五下·丰台期末)兰兰参加了学校的“创意木工坊”。她领取了一根长木条和一块木板制作小木凳。兰兰想将长木条截成4段同样长的短木条做凳腿(如右图所示)。截开后,4 段短木条表面积之和比长木条的表面积增加了 150平方厘米。兰兰领取的这根长木条的体积是多少立方厘米?
21.(2024五下·密云期末)一次书法比赛中,所有参赛者都获了奖。获一等奖的占总数的,获二等奖的占总数的,其余的获三等奖。获三等奖的占总数的儿分之几?
22.(2024五下·丰台期末)端午节是中国的传统节日,粽子是不可或缺的主题。陕西商洛的(hú)叶粽子不仅香气逼人,形状也与众不同,是近似的长方体。张阿姨准备包30 个这样的粽子,买 10m 长的线团够用吗?
23.(2024五下·丰台期末)张叔叔用铝条制作相框。第一次用了米长的铝条,第二次用了米长的铝条,这两次一共用了多长的铝条?
24.(2024五下·密云期末)北京市于2018年提出《打赢蓝天保卫战三年行动计划》后,2021年北京市空气质量首次全面达标。下面是2017年和2021年北京市各月空气质达到优良情况的统计图。
(1)2021年空气质量达到优良天数最多的是 月,有 天。
(2)对比这两年相应各月空气质量达到优良的天数,2021年比 2017 年多的有 个月。
(3)2017年各月空气质量达到优良天数的平均值不到20天。根据图中信息请你估计,2021年各月空气质量达到优良天数的平均值 达到20天。(填“能”或“不能”)
25.(2024五下·密云期末)(如下图)一块长方体木块,从上部和下部分别截去高3厘米和2厘米的小长方体后,成为一个正方体。表面积减少120平方厘米,原来长方体体积是多少立方厘米?
26.(2024五下·密云期末)新建一个游泳池,长50米,宽25米,深2.5米。在游泳池的底面和四周都抹一层水泥,如果每平方米用水泥12千克。至少需要用水泥多少千克?
27.(2024五下·密云期末)把一块长3米的长方体木材,锯成完全相同的两块小长方体。(如下图)表面积增加了40平方分米。这根木材原来的体积是多少立方米?
28.(2024五下·密云期末)一个长方体的礼品盒(如下图),像这样用红色丝带捆扎起来,打结处长30厘米。包扎这个礼品盒至少需要红色丝带多少厘米?(图中单位:厘米)
29.(2024五下·顺义期末)沈阳、三亚两地 2023 年各月平均气温如下图:
①以下是沈阳、三亚两地的资料介绍。
通过这些介绍,在统计图上标出虚线和实线代表的城市。写出你推测的理由:
(1)观察上面折线统计图,2023年1月的平均最低气温,沈阳是 ℃,三亚是 ℃,两地相差 ℃。
(2)温度适宜的地方适合人们旅行,小明全家在出行时想选择气温在18℃~25℃的地方。请你根据统计图中的信息为他们家人去两地旅行提出合理建议。
30.(2024五下·顺义期末)的结果比1大还是比1小?
(1)请你通过计算的方法进行比较。
(2)不计算,请你写出其他比较方法。
答案解析部分
1.解:1--
=-
=
答:最后5分钟行驶的路程是大桥全长的。
最后5分钟行驶的路程是大桥全长的分率=1-前10分钟行驶的分率-又用25分钟行驶的分率。
2.解:20×=8(厘米)
8×=0.05(厘米)
答:血液在静脉中每秒约流动8厘来,血液在毛细血管中每秒约流动0.05厘米。
血液在静脉中每秒约流动的速度=血液在主动脉中大约的流动速度×;血液在毛细血管中每秒约流动的速度=血液在静脉中每秒约流动的速度。
3.解:165÷= 275(个)
275×=99(个)
答:实验小学四收集了99个空矿泉水瓶;六年级收集了275个空矿泉水瓶。
五年级收集的个数÷对应六年级收集个数的分率=六年级收集个数;六年级收集个数×=四年级收集的个数。
4.解:13×4+(13×8+4×8)×2
=13×4+136×2
=52+272
=324(平方分米)
答:制作这个种植箱需要324平方分米木板。
制作这个种植箱需木板的面积=长×宽+(长×高+宽×高)×2。
5.解:4×3×0.5
=12×0.5
=6(立方分米)
答:这块石头的体积是6立方分米。
这块石头的体积=长方体玻璃缸的长×宽×水面下降的高度。
6.(1)解:因为的分数单位是,的分数单位是,分数单位不同,没法直接相加减,所以要先通分,变成同分母分数。
(2)解:300+30=330,相同数位要对齐,也就是相同的计数单位相加减;
300.35+0.3=300.65,小数点对齐,也就是相同数位对齐;
+=+=,先通分,变成分数单位相同的分数,再相加。
(3)解:分数和小数相加应该怎样计算?
(1)分数单位不同,没法直接相加减;需要变成统一的分数单位;
(2)在举例解释时,能从计数单位以及计数单位个数的角度表达出运算一致性的意思即可;
(3)能围绕“分数的加法和减法”单元的内容提问题即可。
7.解:1---
=--
=-
=
<<<
答:豆角的种植面积最小。
胡萝卜占的分率=1-其余各项蔬菜分别占的分率,然后把四种蔬菜占的分率比较大小,得出豆角的种植面积最小。
8.解:设长方体的高是x厘米,则宽是=(15-x)厘米。
15-x=2x
15=3x
x=15÷3
x=5
5×2=10(厘米)
20×10×5
=200×5
=1000(立方厘米)
答:这个长方体的体积是1000立方厘米。
这个长方体的体积=长×宽×高,设长方体的高是x厘米,则宽是=(15-x)厘米。依据高×2=宽,列方程求出高是5厘米,宽=高×2=10厘米,长是20厘米。
9.(1)解:
(2)11;12
(3)解:预测小红 13 岁时的身高可能达到165厘米,因为小红此时身高正处于增长期。
解:(2)小红从11岁到12岁身高增长得很快。
故答案为:(2)11;12。
(1)依据统计表中的数据、图例,描出各点,然后连接成线,并且标上数据;
(2)小红从11岁到12岁的直条最陡峭,说明身高增长得很快;
(3)预测小红 13 岁时的身高可能达到165厘米,因为小红此时身高正处于增长期。
10.解:1--
=-
=
答:还剩全长的没有修。
还剩下没有修的分率=1-第一天修全长的分率-第二天修全长的分率。
11.(1)解:12×11×11
=132×11
=1452(cm3)
答:袋中面包体积为 1452cm3。
(2)解:可以,类比长方体体积公式,相当于底面积乘高。
(3)解:发现(猜想):可类比长方体体积公式,其体积等于底面积乘高。
(1)袋中面包体积=长×宽×高;
(2)物体所占空间的大小叫做它的体积,切开后体积和不变,因为底面是三角形,三角形的面积=底×高÷2,所以体积依旧等于底面积乘高,可以用这种方法计算;
(3)发现(猜想):可类比长方体体积公式,其体积等于底面积乘高。
12.(1)14000
(2)日;6000
(3)解:工作日步数相近,双休日差别大。
解:(1)李叔叔步数最多的那一天走了14000步;
(2)张叔叔和李叔叔星期日步数相差最大;相差:18200-12200=6000(步) 。
故答案为:(1)14000;(2)日;6000。
(1)观察表示李叔叔步数的折线,折线点最高是14000步;
(2)张叔叔和李叔叔星期日步数折线的点相差最大,说明这一天步数相差最大;相差的步数=两人的步数差;
(3)工作日步数相近,双休日差别大。
13.解:8×8×(7-6)
=8×8×1
=64(立方厘米)
答:珊瑚石的体积为64立方厘米。
珊瑚石的体积=正方体容器的棱长×棱长×(放入珊瑚石后水面的高度-放入珊瑚石前水面的高度)。
14.解: +=(克)
答:嫦娥五号着陆器携带的国旗重量是克。
嫦娥五号着陆器携带的国旗重量=嫦娥六号着陆器携带的国旗重量+克。
15.解:15×25×10
=375×10
=3750(立方分米)
3750立方分米=3750升
答:这水箱容积是3750升。
这水箱容积=长×宽×高,然后单位换算。
16.解:
答:金牌和银牌的数量共占总数。
金牌和银牌的数量共占总数的分率=金牌占总数的分率+银牌占总数的分率。
17.(1)解:1-=
答:聪聪再行全程的就能到达学校。
(2)解:-=
答:从图书馆到商店的路程占全程的。
(1)聪聪到达学校再行全程的分率=1-走到商店占全程的分率;
(2) 从图书馆到商店的路程占全程的分率=从家到商店的分率-从家到图书馆的分率。
18.(1)蔬菜
(2)
(3)解:乐乐的体重下降比较快,因为乐乐摄入的蔬菜、果蔬低脂肪的食物较多,肉类较少。
解:(1)乐乐和强强每天摄入蔬菜类食物相差最多;
(2)100÷300=。
故答案为:(1)蔬菜;(2)。
(1)乐乐和强强每天摄入蔬菜类食物的直条相差最远,则说明蔬菜类相差最多;
(2)乐乐每天肉类的摄入量是强强的分率=乐乐每天肉类的摄入量÷强强每天肉类的摄入量;
(3)乐乐的体重下降比较快,因为乐乐摄入的蔬菜、果蔬低脂肪的食物较多,肉类较少。
19.解:长:5+3=8(厘米),宽5厘米,高8厘米。
8×8+(8×5+5×8)×2
=64+(40+40)×2
=64+160
=224(平方厘米)
答:做这个包装盒至少需要224平方厘米纸板。
可以做一个长8厘米、宽5厘米、高8厘米的长方体,做这个包装盒至少需要纸板的面积=长×高+(长×宽+宽×高)×2;其中,长=杯子上杯口的直径+杯子下杯口的直径,宽=杯子上杯口的直径,高=两个摞在一起杯子的高度。
20.解:150÷(3×2)×(20×4)
=150÷6×80
=25×80
=2000(立方厘米)
答:兰兰领取的这根长木条的体积2000立方厘米。
兰兰领取的这根长木条的体积=底面积×高;其中,底面积=增加的表面积÷增加面的个数;高=每根凳子腿的长度×4。
21.解:1--
=-
=
答:获三等奖的占总数的。
获三等奖的占总数的分率=1- 获一等奖的占总数的分率-获二等奖的占总数的分率。
22.解:(4×4+3×4+5)×30
=33×30
=990(厘米)
990厘米=9.9米
9.9<10
答:买10米长的线团够用。
需要线团的长度=(粽子的宽×4+高×4+打结处的长度)×包装的个数,然后与10米比较大小。
23.解:+=(米)
答:这两次一共用了米的铝条。
这两次一共用铝条的长度=第一次用去的长度+第二次用去的长度。
24.(1)12;30
(2)10
(3)能
解:(1)2021年空气质量达到优良天数最多的是12月,有30天;
(2)2021年比 2017 年多的有1月、2月、4月、5月、6月、7月、8月、9月、10月、12月,共10个月;
(3)2021年各月空气质量达到优良天数的平均值能达到20天。
故答案为:(1)12;30;(2)10;(3)能。
(1)观察复式折线统计图,2021年空气质量达到优良天数最多的是12月,有30天;
(2)2021年折线的点高于2017年的有10个月;
(3)2021年各月空气质量达到优良天数的平均值能达到20天,因为除3月最少11天、2月18天外,其余都是24天及以上,所以能达到20天。
25.解:120÷(3+2)÷4
=120÷5÷4
=24÷4
=6(厘米)
6×6×(6+3+2)
=36×11
=396(立方厘米)
答:原来长方体体积是396立方厘米。
原来长方体体积=长×宽×原来的高,其中,长=宽=正方体的棱长=减少的表面积÷(上面减少的高+下面减少的高)÷4=6厘米,原来的高=正方体的棱长+上面减少的高+下面减少的高。
26.解:50×25+(50×2.5+25×2.5)×2
=1250+(125+62.5)×2
=1250+375
=1625(平方米)
1625×12=19500(千克)
答:至少需要用水泥19500千克。
至少需要用水泥的质量=粉刷的面积×平均每平方米需要的质量;其中,粉刷的面积=长×宽+(长×高+宽×高)×2。
27.解:40平方分米=0.4平方米
0.4÷2×3
=0.2×3
=0.6(立方米)
答:这根木材原来的体积是0.6立方米。
这根木材原来的体积=底面积×原来的长;其中,底面积=增加的表面积÷增加面的个数,关键是单位换算。
28.解:40×2+20×4+15×6+30
=80+80+90+30
=160+90+30
=250+30
=280(厘米)
答:捆扎这个礼品盒至少需要红色丝带280厘米。
捆扎这个礼品盒至少需要红色丝带的长度=长×2+宽×4+高×6+打结处的长度。
29.(1)-16;17;33
(2)解:三亚2~4月去比较合适,沈阳7~9月去比较合适,因为此段时间的温度适宜。
解:(1)2023年1月的平均最低气温,沈阳是-16℃,三亚是17℃,两地相差17-(-16)=33(℃)。
故答案为:(1)-16;17;33。
(1)观察复式折线统计图可知:2023年1月的平均最低气温,沈阳是-16℃,三亚是17℃,两地相差的温度=三亚2023年1月的平均最低气温-沈阳2023年1月的平均最低气温;
(2)三亚2~4月去比较合适,沈阳7~9月去比较合适,因为此段时间的温度适宜。
30.(1)解:+=+=
>1
(2)解:>
>
则+>1
(1)异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;
(2)分别观察、与的大小,两个大于的数的和一定大于1。
专练04-解决问题2
一、解决问题
1.(2024五下·期末)2024 年是澳门回归祖国的 25 周年。淘气和同学在六一游学澳门时,汽车正好经过港珠澳大桥。先用10分钟行驶了全长的,又用25 分钟行驶了全长的一半,最后用5分钟通过了大桥。最后5分钟行驶的路程是大桥全长的几分之几?
2.(2024五下·期末)人体血液在主动脉中的流动速度约为20厘米/秒,在静脉中的流动速度约为主动脉中的,血液在静脉中每秒约流动多少厘来?血液在毛细血管中的流动速度大约只有静脉中的,血液在毛细血管中每秒约流动多少厘来?
3.(2023五下·武功期末)”节约资源从我做起”。实验小学上个月开展了收集空矿泉水瓶的活动。五年级收集了165个,是六年级的,四年级收集的个数是六年级的,实验小学四、六年级各收集了多少个空矿泉水瓶?
4.(2024五下·房山期末)工人师傅用木板制作一个长方体种植箱,种植箱的长、宽、高如下图所示,制作这个种植箱需要多少平方分米木板?
5.(2024五下·奉化期末)一个长方体玻璃缸,长4分米,宽3分米,高3分米,把一块不规则石头浸没在水中,水深2分米,捞出这块石头后,水面下降0.5分米,这块石头的体积是多少?
6.(2024五下·朝阳期末)学完第六单元《分数的加法和减法》,同学们提出了一些问题。
(1)请你以为例回答小阳问题,写一写“先通分,再计算”的道理。
(2)请你举例回答小芳的问题,写清整数加法、小数加法和分数加法计算过程中的相同点。
(3)学完这个单元的内容,你还有哪些好奇的问题想要进行研究呢?请在下面至少写出一个问题。
7.(2024五下·房山期末)学校的种植园种了四种蔬菜。其中种植西红柿、豆角、黄瓜的面积与四种蔬菜种植总面积之间的关系如下表所示。
蔬菜种类 西红柿 胡萝卜 豆角 黄瓜
占四种蔬菜种植总面积的几分之几
哪种蔬菜的种植面积最小?请你结合上面的信息,写出思考过程和结果。
8.(2024五下·朝阳期末)丽丽想制作一个长方体纸盒。他先在一张边长为30厘米的正方形纸上绘制出这个长方体纸盒的展开图(如下图)。然后准备将涂色部分裁掉,借助胶条粘贴成长方体。已知长方体的宽是高的2倍,那么这个长方体的体积是多少立方厘米?
9.(2024五下·东城期末)下面是小红7~12岁每年的身高与同龄女学生达标身高的对比统计表。
7 8 9 10 11 12
达标身高/cm 123 128 135 140 148 153
小红身高/cm 112 120 129 139 148 160
根据表中的数据。完成下面各题。
(1)根据表中的数据,把复式折线统计图补充完整。
(2)小红从 岁到 岁身高增长得很快。
(3)请你预测小红 13 岁时的身高并说明理由。
10.(2024五下·东城期末)修一条路,第一天修了全长的。第二天修了全长的,还剩全长的几分之几没有修?
11.(2024五下·房山期末)妈妈给亮亮买了一袋面包,把面看成近似的长方体。
(1)请你求出袋中而包的体积。
(2)你认为下面亮亮求图2面包体积的方法可以吗?写出你的理由。
亮亮在面包上垂直切了一刀,将面包平均分成了两部分,如图1所示,其中一部分(如图2)面包的体积是多少呢?思考后,他用“底面积×高进行了计算。
(3)上面研究了“面包的体积”,关于“求立体图形的体积”你有什么发现或者猜想?请你写一写。
12.(2024五下·房山期末)2023年8月8日是我国第15个“全民健身日”。为践行健康生活方式,张叔叔和李叔叔参与了“每日万步行”健走活动。下图为张叔叔和李叔叔在同一星期内每日步数的统计情况。
(1)李叔叔步数最多的那一天走了 步。
(2)张叔叔和李叔叔星期 步数相差最大、相差 步。
(3)从总体上看,两人这儿天的步数之间明显的差别是什么?
13.(2024五下·房山期末)观察图中信息,计算珊瑚石的体积是多少?
14.(2024五下·朝阳期末)
嫦娥六号着陆器携带的五星红旗在月球表面成功展开。能耐受高真空、高低温循环、强剂量紫外辐照等极端环境的“石头版”高品质织物国旗,是由以玄武岩为主的复合材料制造。嫦娥六号月面展示国旗的大小与嫦娥五号上的国旗规格一样,均为300mm×200mm,与 A4 纸大小相近。
嫦娥六号着陆器携带的国旗重量为克,比嫦娥五号着陆器携带的同规格国旗还要轻克。嫦娥五号着陆器携带的国旗重量是多少克?
15.(2024五下·房山期末)李叔叔用5块铁板制作了一个无盖的长方体水箱,5块铁板的大小如下图所示。这个水箱的容积是多少升?(铁板的厚度忽略不计)
16.(2024五下·房山期末)2022年北京冬季奥运会,中国金牌数首次位居世界三。其中金牌的数量占获得奖牌总数量的,银牌的数量占获得奖牌总数量的。金牌和银牌的数量一共占获得奖牌总数量的儿分之儿?
17.(2024五下·柯桥期末) 星期天, 聪聪从家出发去学校, 行了全程的 到图书馆, 行了全程的 到商店(如图)。
(1)聪聪再行全程的几分之几就能到达学校
(2)从图书馆到商店的路程占全程的几分之几
18.(2024五下·丰台期末)肥胖影响青少年的身心健康。在常规体检中,乐乐和强强的健康状况为“超重”,体检医生提示他们需要加强体育锻炼、注意健康饮食。为此,乐乐和强强每天进行了至少一小时的体育运动,并将一月至五月每天的各类食物摄入量和阶段性的体重监测情况进行了记录,如下面两幅统计图所示:
(1)乐乐和强强每天摄入 类食物相差最多。
(2)乐乐每天肉类的摄入量是强强的 。
(3)请你结合两幅图中的数据判断谁的体重下降的比较快,并分析可能的原因。
19.(2024五下·丰台期末)请你设计一个长方体包装盒,恰好能装下4个探在一起的玻璃杯。为了展示出玻璃杯的样子,前面使用透明塑料膜,其他各面都用纸板。做这个包装盒至少需要多少平方厘米纸板?(纸板厚度和粘接重叠部分忽略不计)
20.(2024五下·丰台期末)兰兰参加了学校的“创意木工坊”。她领取了一根长木条和一块木板制作小木凳。兰兰想将长木条截成4段同样长的短木条做凳腿(如右图所示)。截开后,4 段短木条表面积之和比长木条的表面积增加了 150平方厘米。兰兰领取的这根长木条的体积是多少立方厘米?
21.(2024五下·密云期末)一次书法比赛中,所有参赛者都获了奖。获一等奖的占总数的,获二等奖的占总数的,其余的获三等奖。获三等奖的占总数的儿分之几?
22.(2024五下·丰台期末)端午节是中国的传统节日,粽子是不可或缺的主题。陕西商洛的(hú)叶粽子不仅香气逼人,形状也与众不同,是近似的长方体。张阿姨准备包30 个这样的粽子,买 10m 长的线团够用吗?
23.(2024五下·丰台期末)张叔叔用铝条制作相框。第一次用了米长的铝条,第二次用了米长的铝条,这两次一共用了多长的铝条?
24.(2024五下·密云期末)北京市于2018年提出《打赢蓝天保卫战三年行动计划》后,2021年北京市空气质量首次全面达标。下面是2017年和2021年北京市各月空气质达到优良情况的统计图。
(1)2021年空气质量达到优良天数最多的是 月,有 天。
(2)对比这两年相应各月空气质量达到优良的天数,2021年比 2017 年多的有 个月。
(3)2017年各月空气质量达到优良天数的平均值不到20天。根据图中信息请你估计,2021年各月空气质量达到优良天数的平均值 达到20天。(填“能”或“不能”)
25.(2024五下·密云期末)(如下图)一块长方体木块,从上部和下部分别截去高3厘米和2厘米的小长方体后,成为一个正方体。表面积减少120平方厘米,原来长方体体积是多少立方厘米?
26.(2024五下·密云期末)新建一个游泳池,长50米,宽25米,深2.5米。在游泳池的底面和四周都抹一层水泥,如果每平方米用水泥12千克。至少需要用水泥多少千克?
27.(2024五下·密云期末)把一块长3米的长方体木材,锯成完全相同的两块小长方体。(如下图)表面积增加了40平方分米。这根木材原来的体积是多少立方米?
28.(2024五下·密云期末)一个长方体的礼品盒(如下图),像这样用红色丝带捆扎起来,打结处长30厘米。包扎这个礼品盒至少需要红色丝带多少厘米?(图中单位:厘米)
29.(2024五下·顺义期末)沈阳、三亚两地 2023 年各月平均气温如下图:
①以下是沈阳、三亚两地的资料介绍。
通过这些介绍,在统计图上标出虚线和实线代表的城市。写出你推测的理由:
(1)观察上面折线统计图,2023年1月的平均最低气温,沈阳是 ℃,三亚是 ℃,两地相差 ℃。
(2)温度适宜的地方适合人们旅行,小明全家在出行时想选择气温在18℃~25℃的地方。请你根据统计图中的信息为他们家人去两地旅行提出合理建议。
30.(2024五下·顺义期末)的结果比1大还是比1小?
(1)请你通过计算的方法进行比较。
(2)不计算,请你写出其他比较方法。
答案解析部分
1.解:1--
=-
=
答:最后5分钟行驶的路程是大桥全长的。
最后5分钟行驶的路程是大桥全长的分率=1-前10分钟行驶的分率-又用25分钟行驶的分率。
2.解:20×=8(厘米)
8×=0.05(厘米)
答:血液在静脉中每秒约流动8厘来,血液在毛细血管中每秒约流动0.05厘米。
血液在静脉中每秒约流动的速度=血液在主动脉中大约的流动速度×;血液在毛细血管中每秒约流动的速度=血液在静脉中每秒约流动的速度。
3.解:165÷= 275(个)
275×=99(个)
答:实验小学四收集了99个空矿泉水瓶;六年级收集了275个空矿泉水瓶。
五年级收集的个数÷对应六年级收集个数的分率=六年级收集个数;六年级收集个数×=四年级收集的个数。
4.解:13×4+(13×8+4×8)×2
=13×4+136×2
=52+272
=324(平方分米)
答:制作这个种植箱需要324平方分米木板。
制作这个种植箱需木板的面积=长×宽+(长×高+宽×高)×2。
5.解:4×3×0.5
=12×0.5
=6(立方分米)
答:这块石头的体积是6立方分米。
这块石头的体积=长方体玻璃缸的长×宽×水面下降的高度。
6.(1)解:因为的分数单位是,的分数单位是,分数单位不同,没法直接相加减,所以要先通分,变成同分母分数。
(2)解:300+30=330,相同数位要对齐,也就是相同的计数单位相加减;
300.35+0.3=300.65,小数点对齐,也就是相同数位对齐;
+=+=,先通分,变成分数单位相同的分数,再相加。
(3)解:分数和小数相加应该怎样计算?
(1)分数单位不同,没法直接相加减;需要变成统一的分数单位;
(2)在举例解释时,能从计数单位以及计数单位个数的角度表达出运算一致性的意思即可;
(3)能围绕“分数的加法和减法”单元的内容提问题即可。
7.解:1---
=--
=-
=
<<<
答:豆角的种植面积最小。
胡萝卜占的分率=1-其余各项蔬菜分别占的分率,然后把四种蔬菜占的分率比较大小,得出豆角的种植面积最小。
8.解:设长方体的高是x厘米,则宽是=(15-x)厘米。
15-x=2x
15=3x
x=15÷3
x=5
5×2=10(厘米)
20×10×5
=200×5
=1000(立方厘米)
答:这个长方体的体积是1000立方厘米。
这个长方体的体积=长×宽×高,设长方体的高是x厘米,则宽是=(15-x)厘米。依据高×2=宽,列方程求出高是5厘米,宽=高×2=10厘米,长是20厘米。
9.(1)解:
(2)11;12
(3)解:预测小红 13 岁时的身高可能达到165厘米,因为小红此时身高正处于增长期。
解:(2)小红从11岁到12岁身高增长得很快。
故答案为:(2)11;12。
(1)依据统计表中的数据、图例,描出各点,然后连接成线,并且标上数据;
(2)小红从11岁到12岁的直条最陡峭,说明身高增长得很快;
(3)预测小红 13 岁时的身高可能达到165厘米,因为小红此时身高正处于增长期。
10.解:1--
=-
=
答:还剩全长的没有修。
还剩下没有修的分率=1-第一天修全长的分率-第二天修全长的分率。
11.(1)解:12×11×11
=132×11
=1452(cm3)
答:袋中面包体积为 1452cm3。
(2)解:可以,类比长方体体积公式,相当于底面积乘高。
(3)解:发现(猜想):可类比长方体体积公式,其体积等于底面积乘高。
(1)袋中面包体积=长×宽×高;
(2)物体所占空间的大小叫做它的体积,切开后体积和不变,因为底面是三角形,三角形的面积=底×高÷2,所以体积依旧等于底面积乘高,可以用这种方法计算;
(3)发现(猜想):可类比长方体体积公式,其体积等于底面积乘高。
12.(1)14000
(2)日;6000
(3)解:工作日步数相近,双休日差别大。
解:(1)李叔叔步数最多的那一天走了14000步;
(2)张叔叔和李叔叔星期日步数相差最大;相差:18200-12200=6000(步) 。
故答案为:(1)14000;(2)日;6000。
(1)观察表示李叔叔步数的折线,折线点最高是14000步;
(2)张叔叔和李叔叔星期日步数折线的点相差最大,说明这一天步数相差最大;相差的步数=两人的步数差;
(3)工作日步数相近,双休日差别大。
13.解:8×8×(7-6)
=8×8×1
=64(立方厘米)
答:珊瑚石的体积为64立方厘米。
珊瑚石的体积=正方体容器的棱长×棱长×(放入珊瑚石后水面的高度-放入珊瑚石前水面的高度)。
14.解: +=(克)
答:嫦娥五号着陆器携带的国旗重量是克。
嫦娥五号着陆器携带的国旗重量=嫦娥六号着陆器携带的国旗重量+克。
15.解:15×25×10
=375×10
=3750(立方分米)
3750立方分米=3750升
答:这水箱容积是3750升。
这水箱容积=长×宽×高,然后单位换算。
16.解:
答:金牌和银牌的数量共占总数。
金牌和银牌的数量共占总数的分率=金牌占总数的分率+银牌占总数的分率。
17.(1)解:1-=
答:聪聪再行全程的就能到达学校。
(2)解:-=
答:从图书馆到商店的路程占全程的。
(1)聪聪到达学校再行全程的分率=1-走到商店占全程的分率;
(2) 从图书馆到商店的路程占全程的分率=从家到商店的分率-从家到图书馆的分率。
18.(1)蔬菜
(2)
(3)解:乐乐的体重下降比较快,因为乐乐摄入的蔬菜、果蔬低脂肪的食物较多,肉类较少。
解:(1)乐乐和强强每天摄入蔬菜类食物相差最多;
(2)100÷300=。
故答案为:(1)蔬菜;(2)。
(1)乐乐和强强每天摄入蔬菜类食物的直条相差最远,则说明蔬菜类相差最多;
(2)乐乐每天肉类的摄入量是强强的分率=乐乐每天肉类的摄入量÷强强每天肉类的摄入量;
(3)乐乐的体重下降比较快,因为乐乐摄入的蔬菜、果蔬低脂肪的食物较多,肉类较少。
19.解:长:5+3=8(厘米),宽5厘米,高8厘米。
8×8+(8×5+5×8)×2
=64+(40+40)×2
=64+160
=224(平方厘米)
答:做这个包装盒至少需要224平方厘米纸板。
可以做一个长8厘米、宽5厘米、高8厘米的长方体,做这个包装盒至少需要纸板的面积=长×高+(长×宽+宽×高)×2;其中,长=杯子上杯口的直径+杯子下杯口的直径,宽=杯子上杯口的直径,高=两个摞在一起杯子的高度。
20.解:150÷(3×2)×(20×4)
=150÷6×80
=25×80
=2000(立方厘米)
答:兰兰领取的这根长木条的体积2000立方厘米。
兰兰领取的这根长木条的体积=底面积×高;其中,底面积=增加的表面积÷增加面的个数;高=每根凳子腿的长度×4。
21.解:1--
=-
=
答:获三等奖的占总数的。
获三等奖的占总数的分率=1- 获一等奖的占总数的分率-获二等奖的占总数的分率。
22.解:(4×4+3×4+5)×30
=33×30
=990(厘米)
990厘米=9.9米
9.9<10
答:买10米长的线团够用。
需要线团的长度=(粽子的宽×4+高×4+打结处的长度)×包装的个数,然后与10米比较大小。
23.解:+=(米)
答:这两次一共用了米的铝条。
这两次一共用铝条的长度=第一次用去的长度+第二次用去的长度。
24.(1)12;30
(2)10
(3)能
解:(1)2021年空气质量达到优良天数最多的是12月,有30天;
(2)2021年比 2017 年多的有1月、2月、4月、5月、6月、7月、8月、9月、10月、12月,共10个月;
(3)2021年各月空气质量达到优良天数的平均值能达到20天。
故答案为:(1)12;30;(2)10;(3)能。
(1)观察复式折线统计图,2021年空气质量达到优良天数最多的是12月,有30天;
(2)2021年折线的点高于2017年的有10个月;
(3)2021年各月空气质量达到优良天数的平均值能达到20天,因为除3月最少11天、2月18天外,其余都是24天及以上,所以能达到20天。
25.解:120÷(3+2)÷4
=120÷5÷4
=24÷4
=6(厘米)
6×6×(6+3+2)
=36×11
=396(立方厘米)
答:原来长方体体积是396立方厘米。
原来长方体体积=长×宽×原来的高,其中,长=宽=正方体的棱长=减少的表面积÷(上面减少的高+下面减少的高)÷4=6厘米,原来的高=正方体的棱长+上面减少的高+下面减少的高。
26.解:50×25+(50×2.5+25×2.5)×2
=1250+(125+62.5)×2
=1250+375
=1625(平方米)
1625×12=19500(千克)
答:至少需要用水泥19500千克。
至少需要用水泥的质量=粉刷的面积×平均每平方米需要的质量;其中,粉刷的面积=长×宽+(长×高+宽×高)×2。
27.解:40平方分米=0.4平方米
0.4÷2×3
=0.2×3
=0.6(立方米)
答:这根木材原来的体积是0.6立方米。
这根木材原来的体积=底面积×原来的长;其中,底面积=增加的表面积÷增加面的个数,关键是单位换算。
28.解:40×2+20×4+15×6+30
=80+80+90+30
=160+90+30
=250+30
=280(厘米)
答:捆扎这个礼品盒至少需要红色丝带280厘米。
捆扎这个礼品盒至少需要红色丝带的长度=长×2+宽×4+高×6+打结处的长度。
29.(1)-16;17;33
(2)解:三亚2~4月去比较合适,沈阳7~9月去比较合适,因为此段时间的温度适宜。
解:(1)2023年1月的平均最低气温,沈阳是-16℃,三亚是17℃,两地相差17-(-16)=33(℃)。
故答案为:(1)-16;17;33。
(1)观察复式折线统计图可知:2023年1月的平均最低气温,沈阳是-16℃,三亚是17℃,两地相差的温度=三亚2023年1月的平均最低气温-沈阳2023年1月的平均最低气温;
(2)三亚2~4月去比较合适,沈阳7~9月去比较合适,因为此段时间的温度适宜。
30.(1)解:+=+=
>1
(2)解:>
>
则+>1
(1)异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算;
(2)分别观察、与的大小,两个大于的数的和一定大于1。
同课章节目录
