【期末热点.重难点】棱台(含解析)2024-2025学年人教A版(2019)数学高一下册
文档属性
| 名称 | 【期末热点.重难点】棱台(含解析)2024-2025学年人教A版(2019)数学高一下册 |  | |
| 格式 | docx | ||
| 文件大小 | 537.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 16:55:13 | ||
图片预览




文档简介
期末热点.重难点 棱台
一.选择题(共5小题)
1.(2024春 汉寿县校级期中)下列说法正确的是( )
A.长方体是四棱柱,直四棱柱是长方体
B.有2个面平行,其余各面都是梯形的几何体是棱台
C.各侧面都是正方形的四棱柱一定是正方体
D.棱柱的侧棱相等,侧面都是平行四边形
2.(2024 安徽学业考试)下列关于空间几何体结构特征的描述错误的是( )
A.棱柱的侧棱互相平行
B.以直角三角形的一边为轴旋转一周得到的几何体不一定是圆锥
C.正三棱锥的各个面都是正三角形
D.棱台各侧棱所在直线会交于一点
3.(2024春 桐城市期中)下列说法正确的是( )
A.用一个平行于圆锥底面的平面去截圆锥,该圆锥―定被分为一个小圆锥和一个圆台
B.有两个面互相平行,其余各面是平行四边形的几何体是棱柱
C.圆台的所有母线延长不一定交于一点
D.一个多面体至少有3个面
4.(2024秋 岳麓区校级月考)已知正三棱台ABC﹣A1B1C1所有顶点均在半径为5的半球球面上,且AB=4,A1B1=3,则该三棱台的高为( )
A.1 B.4 C.7 D.1或7
5.(2024春 郊区校级期中)下列命题中正确的是( )
A.梯形的直观图可能是平行四边形
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.有两个面平行且相似,其他各个面都是梯形的多面体是棱台
D.底面是矩形的直平行六面体是长方体
二.多选题(共4小题)
(多选)6.(2025 广东一模)某数学学习小组甲、乙、丙三人分别构建了如图所示的正四棱台①,②,③,从左往右.若上底面边长、下底面边长、高均依次递增dcm,记正四棱台①,②,③的侧棱与底面所成的角分别为α1,α2,α3,正四棱台①,②,③的侧面与底面所成的角分别为θ1,θ2,θ3,则( )
A.sinα1+sinα3=2sinα2 B.tanα1+tanα3=2tanα2
C.cosθ1+cosθ3=2cosθ2 D.tanθ1+tanθ3=2tanθ2
(多选)7.(2024春 吴川市校级期中)下列说法不正确的有( )
A.两个面平行且相似,其余各面都是梯形的多面体是棱台
B.以直角三角形的一边为轴旋转一周所得的旋转体是圆锥
C.各侧面都是正方形的四棱柱一定是正方体
D.圆锥的轴截面是等腰三角形
(多选)8.(2024春 赫章县期中)下面关于空间几何体的表述,正确的是( )
A.棱柱的侧面都是平行四边形
B.直角三角形以其一边所在直线为旋转轴,其余两边旋转一周形成的面所围成的几何体是圆锥
C.正四棱柱一定是长方体
D.用一个平面去截棱锥,底面和截面之间的部分叫做棱台
(多选)9.(2024春 伊宁市期中)下列说法正确的是( )
A.圆柱的所有母线长都相等
B.棱柱的侧棱都相等,侧面都是平行四边形
C.底面是正多边形的棱锥是正棱锥
D.棱台的侧棱延长后必交于一点
三.填空题(共3小题)
10.(2023秋 五莲县校级期末)一个正四棱台的下底面周长与上底面周长之差为16,且其侧面梯形的高为,则该正四棱台的高为 .
11.(2024 四川模拟)在正四棱台ABCD﹣A1B1C1D1内有一个球与该四棱台的每个面都相切,若A1B1=2,AB=4,则该四棱台的高是 .
12.(2024 沙依巴克区校级模拟)若正四棱台的上、下底面边长分别是5和7,对角线长为9,则该棱台的高为 .
四.解答题(共3小题)
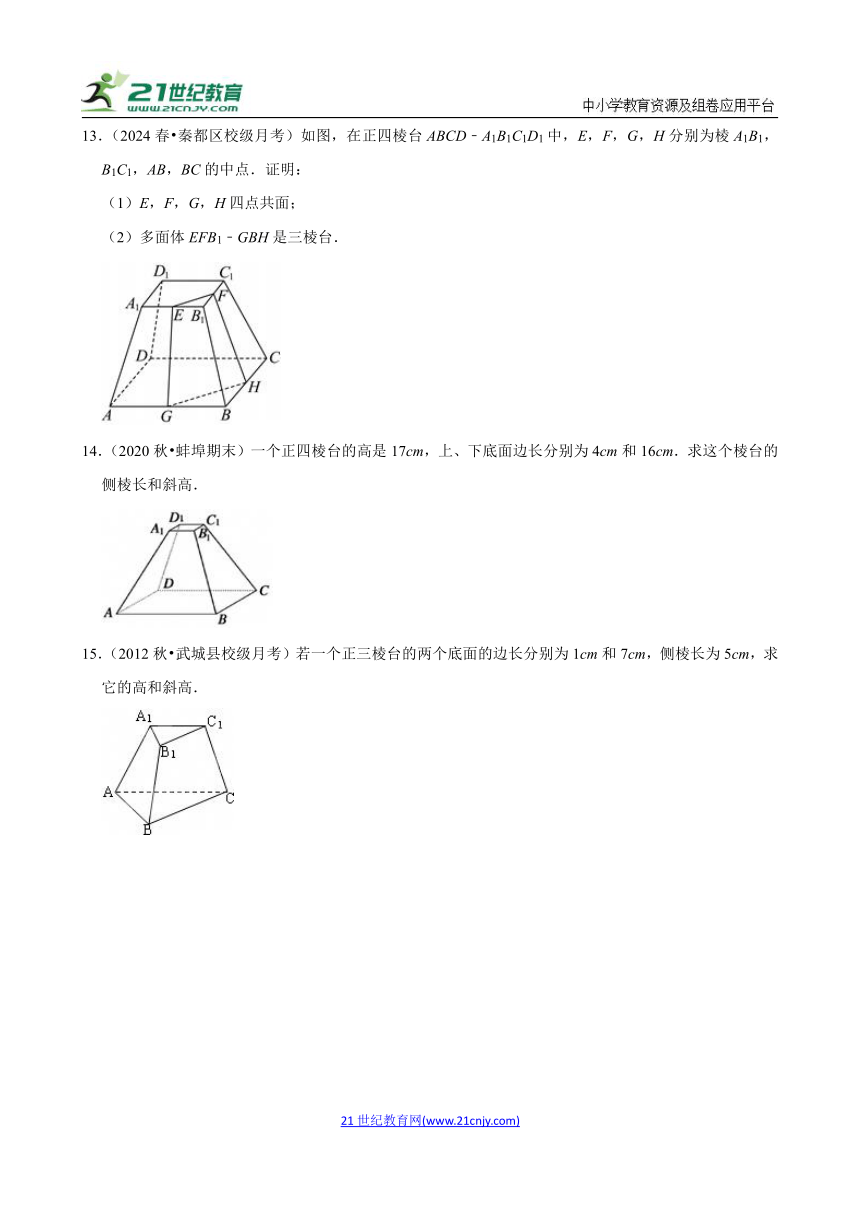
13.(2024春 秦都区校级月考)如图,在正四棱台ABCD﹣A1B1C1D1中,E,F,G,H分别为棱A1B1,B1C1,AB,BC的中点.证明:
(1)E,F,G,H四点共面;
(2)多面体EFB1﹣GBH是三棱台.
14.(2020秋 蚌埠期末)一个正四棱台的高是17cm,上、下底面边长分别为4cm和16cm.求这个棱台的侧棱长和斜高.
15.(2012秋 武城县校级月考)若一个正三棱台的两个底面的边长分别为1cm和7cm,侧棱长为5cm,求它的高和斜高.
期末热点.重难点 棱台
参考答案与试题解析
一.选择题(共5小题)
1.(2024春 汉寿县校级期中)下列说法正确的是( )
A.长方体是四棱柱,直四棱柱是长方体
B.有2个面平行,其余各面都是梯形的几何体是棱台
C.各侧面都是正方形的四棱柱一定是正方体
D.棱柱的侧棱相等,侧面都是平行四边形
【考点】棱台的结构特征;棱柱的结构特征.
【专题】综合题;整体思想;分析法;立体几何;直观想象.
【答案】D
【分析】由多面体、棱台、棱柱等几何体的定义逐项判断即可.
【解答】解:对于A,长方体是四棱柱,但是底面是平行四边形的直棱柱不是长方体,故选项A错误;
对于B,有2个面平行,其余各面都是梯形,但若是各侧棱的延长线不能交于一点,则该几何体不是棱台,故选项B错误;
对于C,各侧面都是正方形的四棱柱,可以是底面为菱形的直棱柱,不一定是正方体,故选项C错误;
对于D,由棱柱定义知,棱柱的各侧棱平行且相等,故侧面是平行四边形,故选项D正确.
故选:D.
【点评】本题考查了棱柱和棱台的几何特征,属于基础题.
2.(2024 安徽学业考试)下列关于空间几何体结构特征的描述错误的是( )
A.棱柱的侧棱互相平行
B.以直角三角形的一边为轴旋转一周得到的几何体不一定是圆锥
C.正三棱锥的各个面都是正三角形
D.棱台各侧棱所在直线会交于一点
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;棱柱的结构特征;棱锥的结构特征.
【专题】转化思想;转化法;空间位置关系与距离;运算求解.
【答案】C
【分析】根据相应几何体的定义和性质判断即可.
【解答】解:根据棱柱的性质可知A正确;
当以直角三角形的斜边所在直线为旋转轴时,所得几何体为两个圆锥的组合体,故B正确;
正三棱锥的底面是正三角形,其余侧面是全等的等腰三角形,故C错误;
棱台是用平行于底面的平面截棱锥而得,故侧棱所在直线必交于一点,D正确.
故选:C.
【点评】本题主要考查几何体的定义和性质,属于基础题.
3.(2024春 桐城市期中)下列说法正确的是( )
A.用一个平行于圆锥底面的平面去截圆锥,该圆锥―定被分为一个小圆锥和一个圆台
B.有两个面互相平行,其余各面是平行四边形的几何体是棱柱
C.圆台的所有母线延长不一定交于一点
D.一个多面体至少有3个面
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;构成空间几何体的基本元素;棱柱的结构特征.
【专题】数形结合;分析法;立体几何;数学抽象.
【答案】A
【分析】根据圆锥、棱柱以及圆台和多面体的定义,一一判断各选项,即得答案.
【解答】解:对于A项,用一个平行于圆锥底面的平面去截圆锥,原圆锥一定被分为一个小圆锥和一个圆台,故A正确;
对于B项,满足条件的几何体可能是组合体,如图,故B错误;
对于C项,圆台的所有母线延长一定交于一点,故C错误;
对于D项,多面体至少有4个面,所以D错误.
故选:A.
【点评】本题考查了立体几何的相关知识,注意棱台,圆台等几何体的结构特征,属于中档题.
4.(2024秋 岳麓区校级月考)已知正三棱台ABC﹣A1B1C1所有顶点均在半径为5的半球球面上,且AB=4,A1B1=3,则该三棱台的高为( )
A.1 B.4 C.7 D.1或7
【考点】棱台的结构特征.
【专题】转化思想;转化法;立体几何;空间想象.
【答案】A
【分析】分别求得上下底面所在平面截球所得圆的半径,找到过球心,上下底面所在外接圆圆心的截面,根据勾股关系可得球心到三棱台上下底面的距离,得解.
【解答】解:根据题意,正三棱台ABC﹣A1B1C1中,AB=4,A1B1=3,
所以上下底面所在外接圆的半径分别为r1=3,r2=4,
过点A,A1,O1,O2的截面如图:
,,
∴h=OO2﹣OO1=1.
故选:A.
【点评】本题考查棱台的结构特征,属于中档题.
5.(2024春 郊区校级期中)下列命题中正确的是( )
A.梯形的直观图可能是平行四边形
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.有两个面平行且相似,其他各个面都是梯形的多面体是棱台
D.底面是矩形的直平行六面体是长方体
【考点】棱台的结构特征;圆锥的结构特征;平面图形的直观图.
【专题】对应思想;定义法;立体几何;逻辑思维.
【答案】D
【分析】根据斜二测画法判断选项A,
根据过圆锥顶点的截面图形特征和截面图的面积公式判断选项B,
根据棱台的定义判断选项C,
根据直棱柱的定义判断选项D.
【解答】解:对于A,因为梯形平行的一组对边长度不相等,所以它们的直观图的长度也不相等,
即梯形的直观图不可能是平行四边形,选项A错误;
对于B,过圆锥顶点的截面为等腰三角形,且两腰长为母线长l,
设该等腰三角形顶角为θ,则截面三角形面积为,显然当,面积S最大,
所以当圆锥的轴截面三角形顶角大于时,圆锥的轴截面面积不是最大的,选项B错误;
对于C,根据棱台的定义,棱台的侧棱延伸后必须交于同一点,选项C错误;
对于D,底面是矩形的直平行六面体是长方体,选项D正确.
故选:D.
【点评】本题考查了空间几何体的结构特征应用问题,是基础题.
二.多选题(共4小题)
(多选)6.(2025 广东一模)某数学学习小组甲、乙、丙三人分别构建了如图所示的正四棱台①,②,③,从左往右.若上底面边长、下底面边长、高均依次递增dcm,记正四棱台①,②,③的侧棱与底面所成的角分别为α1,α2,α3,正四棱台①,②,③的侧面与底面所成的角分别为θ1,θ2,θ3,则( )
A.sinα1+sinα3=2sinα2 B.tanα1+tanα3=2tanα2
C.cosθ1+cosθ3=2cosθ2 D.tanθ1+tanθ3=2tanθ2
【考点】棱台的结构特征.
【专题】计算题;转化思想;综合法;立体几何;运算求解.
【答案】BD
【分析】先根据正四棱台的特点,分别求出侧棱和底面所成角和侧面和底面所成角,然后分别求出对应的角的正弦余弦和正切值,再对照各选项中的等式进行验证,即可得到本题的答案.
【解答】解:根据题意,作出正四棱台ABCD﹣A1B1C1D1,如图所示,连接BD,
设点B在平面ABCD内的射影为点O,则点O在线段BD上,过B1作B1M⊥BC,交BC于M点,连接MO,
由图可知侧棱与底面所成的角为∠B1BO,因为B1O⊥底面ABCD,BC 平面ABCD,所以B1O⊥BC,
又因为B1M⊥BC,且B1M 平面B1OM,B1O 平面B1OM,B1O∩BM=B,所以BC⊥平面B1OM,
而OM 平面B1OM,所以BC⊥OM,所以∠B1MO为平面B1C1CB与平面ABCD的夹角,即为四棱台的侧面与底面所成角.
令图①四棱台高为h,上下底面边长分别为a、b,
对于A,,同理可得,.
因此,sinα1+sinα3≠2sinα2,A项不正确;
对于B,,同理可得所以tanα1+tanα3=2tanα2,B正确;
对于C,,同理可得,.
所以cosθ1+cosθ3≠2cosθ2,C项不正确;
对于D,,同理可得,,可得等式tanθ1+tanθ3=2tanθ2成立,故D正确.
故选:BD.
【点评】本题主要考查棱台的结构特征、直线与平面所成角和二面角的求法、锐角三角函数的应用,考查了计算能力、图形的理解能力,属于中档题.
(多选)7.(2024春 吴川市校级期中)下列说法不正确的有( )
A.两个面平行且相似,其余各面都是梯形的多面体是棱台
B.以直角三角形的一边为轴旋转一周所得的旋转体是圆锥
C.各侧面都是正方形的四棱柱一定是正方体
D.圆锥的轴截面是等腰三角形
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;命题的真假判断与应用;棱柱的结构特征.
【专题】数形结合;综合法;空间位置关系与距离;逻辑思维.
【答案】ABC
【分析】根据棱台的定义判断A;根据圆锥的定义判断B;根据正方体的定义判断C;根据圆锥的结构特征判断D.
【解答】解:对于A,棱台是棱锥过侧棱上一点作底面的平行平面分割而得到的,
而两个平面平行且相似,其余各面都是梯形的多面体中,把梯形的腰延长后,
有可能不交于一点,就不是棱台,故A错误;
对于B,以直角三角形的斜边为轴,旋转一周所得的旋转体不是圆锥,故B错误;
对于C,各侧面都是正方形的四棱柱中,底面有可能是菱形,不一定是正方体,故C错误;
对于D,由圆锥的结构特征得:圆锥的轴截面是等腰三角形,故D正确.
故选:ABC.
【点评】本题考查命题真假的判断,考查棱台、圆锥、正方体、圆锥的定义、性质等基础知识,是基础题.
(多选)8.(2024春 赫章县期中)下面关于空间几何体的表述,正确的是( )
A.棱柱的侧面都是平行四边形
B.直角三角形以其一边所在直线为旋转轴,其余两边旋转一周形成的面所围成的几何体是圆锥
C.正四棱柱一定是长方体
D.用一个平面去截棱锥,底面和截面之间的部分叫做棱台
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;棱柱的结构特征;棱锥的结构特征.
【专题】对应思想;综合法;立体几何;逻辑思维.
【答案】AC
【分析】用简单几何体的定义及特征去逐个判断即可.
【解答】解:对于A:棱柱的所有侧面都是平行四边形,且每相邻两个四边形的公共边都相互平行,故A正确;
对于B:只有以直角边为旋转轴旋转才能得到圆锥,以斜边为旋转轴旋转得到的是两个圆锥的组合体,故B错误;
对于C:正四棱柱是底面是正方形的直四棱柱,所以必然是长方体,故C正确;
对于D:只有截面与底面平行时,截面与底面之间的部分才是棱台,故D错误.
故选:AC.
【点评】本题主要考查空间几何体的结构特征,属于基础题.
(多选)9.(2024春 伊宁市期中)下列说法正确的是( )
A.圆柱的所有母线长都相等
B.棱柱的侧棱都相等,侧面都是平行四边形
C.底面是正多边形的棱锥是正棱锥
D.棱台的侧棱延长后必交于一点
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;命题的真假判断与应用;棱柱的结构特征;棱锥的结构特征.
【专题】整体思想;综合法;立体几何;直观想象.
【答案】ABD
【分析】根据圆柱,棱柱,正棱锥以及棱台的结构特征,逐个判断各个选项即可.
【解答】解:对于A,由圆柱的结构特征可知,圆柱的所有母线长都相等,故A正确;
对于B,由棱柱的结构特征可知,棱柱的侧棱都相等,侧面都是平行四边形,故B正确;
对于C,底面是正多边形,且侧面是全等的等腰三角形的棱锥是正棱锥,故C错误;
对于D,由棱台的定义可知,棱台的侧棱延长后必交于一点,故D正确.
故选:ABD.
【点评】本题主要考查了简单几何体的结构特征,属于基础题.
三.填空题(共3小题)
10.(2023秋 五莲县校级期末)一个正四棱台的下底面周长与上底面周长之差为16,且其侧面梯形的高为,则该正四棱台的高为 .
【考点】棱台的结构特征;棱柱、棱锥、棱台的体积.
【专题】计算题;转化思想;综合法;立体几何;运算求解.
【答案】.
【分析】根据题意,利用正四棱台的几何性质,结合勾股定理求解,即可得到本题的答案.
【解答】解:在正四棱台ABCD﹣EFGH,EQ、OM分别为侧面上的高以及棱台的高,
设棱台的上下底面的边长分别为a、b,则4b﹣4a=16,可得b﹣a=4,
在等腰梯形ABFE中,,
等腰梯形AEGC中,过E作EN⊥AC,垂足为N,
可得,即棱台的高为.
故答案为:.
【点评】本题主要考查正四棱台的结构特征、勾股定理与等腰梯形的性质等知识,考查了计算能力、空间想象能力,属于基础题.
11.(2024 四川模拟)在正四棱台ABCD﹣A1B1C1D1内有一个球与该四棱台的每个面都相切,若A1B1=2,AB=4,则该四棱台的高是 .
【考点】棱台的结构特征;点、线、面间的距离计算.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】.
【分析】根据题意,作出正棱台以及球的截面图,作辅助线结合圆的切线性质,求得球的半径,即可求得答案.
【解答】解:根据题意,设球O与上底面、下底面分别切于点O1,O2,与面ADD1A1,面BCC1B1分别切于点E、F,
其截面如图所示:
则MO1=ME=1,EN=NO2=2,
于是,MN=1+2=3,
过点M作MH⊥O2N于点H,则NH=NO2﹣MO1=1,
由勾股定理可得:,
所以,
所以该四棱台的高是.
故答案为:.
【点评】本题考查圆台、球的结构特征,关键是作出圆台、球的轴截面,属于基础题.
12.(2024 沙依巴克区校级模拟)若正四棱台的上、下底面边长分别是5和7,对角线长为9,则该棱台的高为 3 .
【考点】棱台的结构特征.
【专题】转化思想;数形结合法;空间位置关系与距离;直观想象;运算求解.
【答案】见试题解答内容
【分析】利用正四棱台的对角面为等腰梯形,再根据条件即可求出结果.
【解答】解:由题意,正四棱台的对角面为等腰梯形,
其中上底长为5,下底长为7,对角线长为9,
则高为3.
故答案为:3.
【点评】本题考查棱台的结构特征,属基础题.
四.解答题(共3小题)
13.(2024春 秦都区校级月考)如图,在正四棱台ABCD﹣A1B1C1D1中,E,F,G,H分别为棱A1B1,B1C1,AB,BC的中点.证明:
(1)E,F,G,H四点共面;
(2)多面体EFB1﹣GBH是三棱台.
【考点】棱台的结构特征;平面的基本性质及推论.
【专题】转化思想;转化法;立体几何;运算求解.
【答案】(1)证明见解析;(2)证明见解析.
【分析】(1)作出辅助线,得到线线平行,得到四点共面;
(2)作出辅助线,得到四边形EFHG为梯形,延长GE、HF,则GE与HF必相交,不妨设EG∩FH=P,由点线面的关系得到P∈BB1,故GE,FH,B1B交于一点,由平面EFB1∥平面GBH,得到多面体EFB1﹣GBH是三棱台.
【解答】解:(1)证明:连接AC,A1C1,如图所示,
在正四棱台ABCD﹣A1B1C1D1中,A1C1∥AC,
∵E,F,G,H分别为棱A1B1,B1C1,AB,BC的中点,
∴EF∥A1C1,GH∥AC,∴EF∥GH,
∴E,F,G,H四点共面.
(2)证明:∵A1C1≠AC,∴EF≠GH,且EF∥GH,
∴四边形EFHG为梯形,
延长GE、HF,则GE与HF必相交,不妨设EG∩FH=P,
∵GE 平面AA1B1B,∴P∈平面AA1B1B,
∵HF 平面BB1C1C,∴P∈平面BB1C1C,
又∵平面AA1B1B∩平面BB1C1C=BB1,∴P∈BB1,
∴GE,FH,B1B交于一点,
又平面EFB1∥平面GBH,
∴多面体EFB1﹣GBH是三棱台.
【点评】本题考查几何体的结构特征,属于中档题.
14.(2020秋 蚌埠期末)一个正四棱台的高是17cm,上、下底面边长分别为4cm和16cm.求这个棱台的侧棱长和斜高.
【考点】棱台的结构特征.
【专题】数形结合;综合法;空间位置关系与距离.
【答案】见试题解答内容
【分析】设棱台的两底面的中心分别是O1、O,B1C1和BC的中点分别是E1和E,连接O1O、E1E、O1B1、OB、O1E1、OE,则四边形OBB1O1和OEE1O1都是直角梯形.由此能求出这个棱台的侧棱长和斜高.
【解答】解:如图所示,设棱台的两底面的中心分别是O1、O,B1C1和BC的中点分别是E1和E,
连接O1O、E1E、O1B1、OB、O1E1、OE,
则四边形OBB1O1和OEE1O1都是直角梯形.
∵A1B1=4 cm,AB=16 cm,
∴O1E1=2 cm,OE=8 cm,
O1B1=2 cm,OB=8 cm,
∴B1B2=O1O2+(OB﹣O1B1)2=361 cm2,
E1E2=O1O2+(OE﹣O1E1)2=325cm2,
∴B1B=19 cm,E1E=5cm.
∴这个棱台的侧棱长为19cm,斜高为5cm.
【点评】本题考查棱台的侧棱长和斜高的求法,是基础题,解题时要认真审题,注意正四棱台的结构特征的合理运用.
15.(2012秋 武城县校级月考)若一个正三棱台的两个底面的边长分别为1cm和7cm,侧棱长为5cm,求它的高和斜高.
【考点】棱台的结构特征.
【专题】空间位置关系与距离.
【答案】见试题解答内容
【分析】画出正三棱台的图形,连接上下底面中心,就是棱台的高,求出AE,利用勾股定理,求出A′E即可.在侧面等腰梯形中,计算出棱台的斜高的长度.
【解答】解:如图,设正三棱台的上下底的中心分别为O、O1,
连接上下底面中心OO1,
则AE2,AA′=5,
所以A′E=OO1,
即它的高为;
作出一个侧面等腰梯形的高,也是棱台的斜高,
则由等腰梯形的性质,
可得斜高h'4.
【点评】本题给出正三棱台棱台上下底面边长和侧棱长,求三棱台的高和斜高,着重考查了正棱台的结构特征,属于基础题.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024春 汉寿县校级期中)下列说法正确的是( )
A.长方体是四棱柱,直四棱柱是长方体
B.有2个面平行,其余各面都是梯形的几何体是棱台
C.各侧面都是正方形的四棱柱一定是正方体
D.棱柱的侧棱相等,侧面都是平行四边形
2.(2024 安徽学业考试)下列关于空间几何体结构特征的描述错误的是( )
A.棱柱的侧棱互相平行
B.以直角三角形的一边为轴旋转一周得到的几何体不一定是圆锥
C.正三棱锥的各个面都是正三角形
D.棱台各侧棱所在直线会交于一点
3.(2024春 桐城市期中)下列说法正确的是( )
A.用一个平行于圆锥底面的平面去截圆锥,该圆锥―定被分为一个小圆锥和一个圆台
B.有两个面互相平行,其余各面是平行四边形的几何体是棱柱
C.圆台的所有母线延长不一定交于一点
D.一个多面体至少有3个面
4.(2024秋 岳麓区校级月考)已知正三棱台ABC﹣A1B1C1所有顶点均在半径为5的半球球面上,且AB=4,A1B1=3,则该三棱台的高为( )
A.1 B.4 C.7 D.1或7
5.(2024春 郊区校级期中)下列命题中正确的是( )
A.梯形的直观图可能是平行四边形
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.有两个面平行且相似,其他各个面都是梯形的多面体是棱台
D.底面是矩形的直平行六面体是长方体
二.多选题(共4小题)
(多选)6.(2025 广东一模)某数学学习小组甲、乙、丙三人分别构建了如图所示的正四棱台①,②,③,从左往右.若上底面边长、下底面边长、高均依次递增dcm,记正四棱台①,②,③的侧棱与底面所成的角分别为α1,α2,α3,正四棱台①,②,③的侧面与底面所成的角分别为θ1,θ2,θ3,则( )
A.sinα1+sinα3=2sinα2 B.tanα1+tanα3=2tanα2
C.cosθ1+cosθ3=2cosθ2 D.tanθ1+tanθ3=2tanθ2
(多选)7.(2024春 吴川市校级期中)下列说法不正确的有( )
A.两个面平行且相似,其余各面都是梯形的多面体是棱台
B.以直角三角形的一边为轴旋转一周所得的旋转体是圆锥
C.各侧面都是正方形的四棱柱一定是正方体
D.圆锥的轴截面是等腰三角形
(多选)8.(2024春 赫章县期中)下面关于空间几何体的表述,正确的是( )
A.棱柱的侧面都是平行四边形
B.直角三角形以其一边所在直线为旋转轴,其余两边旋转一周形成的面所围成的几何体是圆锥
C.正四棱柱一定是长方体
D.用一个平面去截棱锥,底面和截面之间的部分叫做棱台
(多选)9.(2024春 伊宁市期中)下列说法正确的是( )
A.圆柱的所有母线长都相等
B.棱柱的侧棱都相等,侧面都是平行四边形
C.底面是正多边形的棱锥是正棱锥
D.棱台的侧棱延长后必交于一点
三.填空题(共3小题)
10.(2023秋 五莲县校级期末)一个正四棱台的下底面周长与上底面周长之差为16,且其侧面梯形的高为,则该正四棱台的高为 .
11.(2024 四川模拟)在正四棱台ABCD﹣A1B1C1D1内有一个球与该四棱台的每个面都相切,若A1B1=2,AB=4,则该四棱台的高是 .
12.(2024 沙依巴克区校级模拟)若正四棱台的上、下底面边长分别是5和7,对角线长为9,则该棱台的高为 .
四.解答题(共3小题)
13.(2024春 秦都区校级月考)如图,在正四棱台ABCD﹣A1B1C1D1中,E,F,G,H分别为棱A1B1,B1C1,AB,BC的中点.证明:
(1)E,F,G,H四点共面;
(2)多面体EFB1﹣GBH是三棱台.
14.(2020秋 蚌埠期末)一个正四棱台的高是17cm,上、下底面边长分别为4cm和16cm.求这个棱台的侧棱长和斜高.
15.(2012秋 武城县校级月考)若一个正三棱台的两个底面的边长分别为1cm和7cm,侧棱长为5cm,求它的高和斜高.
期末热点.重难点 棱台
参考答案与试题解析
一.选择题(共5小题)
1.(2024春 汉寿县校级期中)下列说法正确的是( )
A.长方体是四棱柱,直四棱柱是长方体
B.有2个面平行,其余各面都是梯形的几何体是棱台
C.各侧面都是正方形的四棱柱一定是正方体
D.棱柱的侧棱相等,侧面都是平行四边形
【考点】棱台的结构特征;棱柱的结构特征.
【专题】综合题;整体思想;分析法;立体几何;直观想象.
【答案】D
【分析】由多面体、棱台、棱柱等几何体的定义逐项判断即可.
【解答】解:对于A,长方体是四棱柱,但是底面是平行四边形的直棱柱不是长方体,故选项A错误;
对于B,有2个面平行,其余各面都是梯形,但若是各侧棱的延长线不能交于一点,则该几何体不是棱台,故选项B错误;
对于C,各侧面都是正方形的四棱柱,可以是底面为菱形的直棱柱,不一定是正方体,故选项C错误;
对于D,由棱柱定义知,棱柱的各侧棱平行且相等,故侧面是平行四边形,故选项D正确.
故选:D.
【点评】本题考查了棱柱和棱台的几何特征,属于基础题.
2.(2024 安徽学业考试)下列关于空间几何体结构特征的描述错误的是( )
A.棱柱的侧棱互相平行
B.以直角三角形的一边为轴旋转一周得到的几何体不一定是圆锥
C.正三棱锥的各个面都是正三角形
D.棱台各侧棱所在直线会交于一点
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;棱柱的结构特征;棱锥的结构特征.
【专题】转化思想;转化法;空间位置关系与距离;运算求解.
【答案】C
【分析】根据相应几何体的定义和性质判断即可.
【解答】解:根据棱柱的性质可知A正确;
当以直角三角形的斜边所在直线为旋转轴时,所得几何体为两个圆锥的组合体,故B正确;
正三棱锥的底面是正三角形,其余侧面是全等的等腰三角形,故C错误;
棱台是用平行于底面的平面截棱锥而得,故侧棱所在直线必交于一点,D正确.
故选:C.
【点评】本题主要考查几何体的定义和性质,属于基础题.
3.(2024春 桐城市期中)下列说法正确的是( )
A.用一个平行于圆锥底面的平面去截圆锥,该圆锥―定被分为一个小圆锥和一个圆台
B.有两个面互相平行,其余各面是平行四边形的几何体是棱柱
C.圆台的所有母线延长不一定交于一点
D.一个多面体至少有3个面
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;构成空间几何体的基本元素;棱柱的结构特征.
【专题】数形结合;分析法;立体几何;数学抽象.
【答案】A
【分析】根据圆锥、棱柱以及圆台和多面体的定义,一一判断各选项,即得答案.
【解答】解:对于A项,用一个平行于圆锥底面的平面去截圆锥,原圆锥一定被分为一个小圆锥和一个圆台,故A正确;
对于B项,满足条件的几何体可能是组合体,如图,故B错误;
对于C项,圆台的所有母线延长一定交于一点,故C错误;
对于D项,多面体至少有4个面,所以D错误.
故选:A.
【点评】本题考查了立体几何的相关知识,注意棱台,圆台等几何体的结构特征,属于中档题.
4.(2024秋 岳麓区校级月考)已知正三棱台ABC﹣A1B1C1所有顶点均在半径为5的半球球面上,且AB=4,A1B1=3,则该三棱台的高为( )
A.1 B.4 C.7 D.1或7
【考点】棱台的结构特征.
【专题】转化思想;转化法;立体几何;空间想象.
【答案】A
【分析】分别求得上下底面所在平面截球所得圆的半径,找到过球心,上下底面所在外接圆圆心的截面,根据勾股关系可得球心到三棱台上下底面的距离,得解.
【解答】解:根据题意,正三棱台ABC﹣A1B1C1中,AB=4,A1B1=3,
所以上下底面所在外接圆的半径分别为r1=3,r2=4,
过点A,A1,O1,O2的截面如图:
,,
∴h=OO2﹣OO1=1.
故选:A.
【点评】本题考查棱台的结构特征,属于中档题.
5.(2024春 郊区校级期中)下列命题中正确的是( )
A.梯形的直观图可能是平行四边形
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.有两个面平行且相似,其他各个面都是梯形的多面体是棱台
D.底面是矩形的直平行六面体是长方体
【考点】棱台的结构特征;圆锥的结构特征;平面图形的直观图.
【专题】对应思想;定义法;立体几何;逻辑思维.
【答案】D
【分析】根据斜二测画法判断选项A,
根据过圆锥顶点的截面图形特征和截面图的面积公式判断选项B,
根据棱台的定义判断选项C,
根据直棱柱的定义判断选项D.
【解答】解:对于A,因为梯形平行的一组对边长度不相等,所以它们的直观图的长度也不相等,
即梯形的直观图不可能是平行四边形,选项A错误;
对于B,过圆锥顶点的截面为等腰三角形,且两腰长为母线长l,
设该等腰三角形顶角为θ,则截面三角形面积为,显然当,面积S最大,
所以当圆锥的轴截面三角形顶角大于时,圆锥的轴截面面积不是最大的,选项B错误;
对于C,根据棱台的定义,棱台的侧棱延伸后必须交于同一点,选项C错误;
对于D,底面是矩形的直平行六面体是长方体,选项D正确.
故选:D.
【点评】本题考查了空间几何体的结构特征应用问题,是基础题.
二.多选题(共4小题)
(多选)6.(2025 广东一模)某数学学习小组甲、乙、丙三人分别构建了如图所示的正四棱台①,②,③,从左往右.若上底面边长、下底面边长、高均依次递增dcm,记正四棱台①,②,③的侧棱与底面所成的角分别为α1,α2,α3,正四棱台①,②,③的侧面与底面所成的角分别为θ1,θ2,θ3,则( )
A.sinα1+sinα3=2sinα2 B.tanα1+tanα3=2tanα2
C.cosθ1+cosθ3=2cosθ2 D.tanθ1+tanθ3=2tanθ2
【考点】棱台的结构特征.
【专题】计算题;转化思想;综合法;立体几何;运算求解.
【答案】BD
【分析】先根据正四棱台的特点,分别求出侧棱和底面所成角和侧面和底面所成角,然后分别求出对应的角的正弦余弦和正切值,再对照各选项中的等式进行验证,即可得到本题的答案.
【解答】解:根据题意,作出正四棱台ABCD﹣A1B1C1D1,如图所示,连接BD,
设点B在平面ABCD内的射影为点O,则点O在线段BD上,过B1作B1M⊥BC,交BC于M点,连接MO,
由图可知侧棱与底面所成的角为∠B1BO,因为B1O⊥底面ABCD,BC 平面ABCD,所以B1O⊥BC,
又因为B1M⊥BC,且B1M 平面B1OM,B1O 平面B1OM,B1O∩BM=B,所以BC⊥平面B1OM,
而OM 平面B1OM,所以BC⊥OM,所以∠B1MO为平面B1C1CB与平面ABCD的夹角,即为四棱台的侧面与底面所成角.
令图①四棱台高为h,上下底面边长分别为a、b,
对于A,,同理可得,.
因此,sinα1+sinα3≠2sinα2,A项不正确;
对于B,,同理可得所以tanα1+tanα3=2tanα2,B正确;
对于C,,同理可得,.
所以cosθ1+cosθ3≠2cosθ2,C项不正确;
对于D,,同理可得,,可得等式tanθ1+tanθ3=2tanθ2成立,故D正确.
故选:BD.
【点评】本题主要考查棱台的结构特征、直线与平面所成角和二面角的求法、锐角三角函数的应用,考查了计算能力、图形的理解能力,属于中档题.
(多选)7.(2024春 吴川市校级期中)下列说法不正确的有( )
A.两个面平行且相似,其余各面都是梯形的多面体是棱台
B.以直角三角形的一边为轴旋转一周所得的旋转体是圆锥
C.各侧面都是正方形的四棱柱一定是正方体
D.圆锥的轴截面是等腰三角形
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;命题的真假判断与应用;棱柱的结构特征.
【专题】数形结合;综合法;空间位置关系与距离;逻辑思维.
【答案】ABC
【分析】根据棱台的定义判断A;根据圆锥的定义判断B;根据正方体的定义判断C;根据圆锥的结构特征判断D.
【解答】解:对于A,棱台是棱锥过侧棱上一点作底面的平行平面分割而得到的,
而两个平面平行且相似,其余各面都是梯形的多面体中,把梯形的腰延长后,
有可能不交于一点,就不是棱台,故A错误;
对于B,以直角三角形的斜边为轴,旋转一周所得的旋转体不是圆锥,故B错误;
对于C,各侧面都是正方形的四棱柱中,底面有可能是菱形,不一定是正方体,故C错误;
对于D,由圆锥的结构特征得:圆锥的轴截面是等腰三角形,故D正确.
故选:ABC.
【点评】本题考查命题真假的判断,考查棱台、圆锥、正方体、圆锥的定义、性质等基础知识,是基础题.
(多选)8.(2024春 赫章县期中)下面关于空间几何体的表述,正确的是( )
A.棱柱的侧面都是平行四边形
B.直角三角形以其一边所在直线为旋转轴,其余两边旋转一周形成的面所围成的几何体是圆锥
C.正四棱柱一定是长方体
D.用一个平面去截棱锥,底面和截面之间的部分叫做棱台
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;棱柱的结构特征;棱锥的结构特征.
【专题】对应思想;综合法;立体几何;逻辑思维.
【答案】AC
【分析】用简单几何体的定义及特征去逐个判断即可.
【解答】解:对于A:棱柱的所有侧面都是平行四边形,且每相邻两个四边形的公共边都相互平行,故A正确;
对于B:只有以直角边为旋转轴旋转才能得到圆锥,以斜边为旋转轴旋转得到的是两个圆锥的组合体,故B错误;
对于C:正四棱柱是底面是正方形的直四棱柱,所以必然是长方体,故C正确;
对于D:只有截面与底面平行时,截面与底面之间的部分才是棱台,故D错误.
故选:AC.
【点评】本题主要考查空间几何体的结构特征,属于基础题.
(多选)9.(2024春 伊宁市期中)下列说法正确的是( )
A.圆柱的所有母线长都相等
B.棱柱的侧棱都相等,侧面都是平行四边形
C.底面是正多边形的棱锥是正棱锥
D.棱台的侧棱延长后必交于一点
【考点】棱台的结构特征;旋转体(圆柱、圆锥、圆台)的体积;命题的真假判断与应用;棱柱的结构特征;棱锥的结构特征.
【专题】整体思想;综合法;立体几何;直观想象.
【答案】ABD
【分析】根据圆柱,棱柱,正棱锥以及棱台的结构特征,逐个判断各个选项即可.
【解答】解:对于A,由圆柱的结构特征可知,圆柱的所有母线长都相等,故A正确;
对于B,由棱柱的结构特征可知,棱柱的侧棱都相等,侧面都是平行四边形,故B正确;
对于C,底面是正多边形,且侧面是全等的等腰三角形的棱锥是正棱锥,故C错误;
对于D,由棱台的定义可知,棱台的侧棱延长后必交于一点,故D正确.
故选:ABD.
【点评】本题主要考查了简单几何体的结构特征,属于基础题.
三.填空题(共3小题)
10.(2023秋 五莲县校级期末)一个正四棱台的下底面周长与上底面周长之差为16,且其侧面梯形的高为,则该正四棱台的高为 .
【考点】棱台的结构特征;棱柱、棱锥、棱台的体积.
【专题】计算题;转化思想;综合法;立体几何;运算求解.
【答案】.
【分析】根据题意,利用正四棱台的几何性质,结合勾股定理求解,即可得到本题的答案.
【解答】解:在正四棱台ABCD﹣EFGH,EQ、OM分别为侧面上的高以及棱台的高,
设棱台的上下底面的边长分别为a、b,则4b﹣4a=16,可得b﹣a=4,
在等腰梯形ABFE中,,
等腰梯形AEGC中,过E作EN⊥AC,垂足为N,
可得,即棱台的高为.
故答案为:.
【点评】本题主要考查正四棱台的结构特征、勾股定理与等腰梯形的性质等知识,考查了计算能力、空间想象能力,属于基础题.
11.(2024 四川模拟)在正四棱台ABCD﹣A1B1C1D1内有一个球与该四棱台的每个面都相切,若A1B1=2,AB=4,则该四棱台的高是 .
【考点】棱台的结构特征;点、线、面间的距离计算.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】.
【分析】根据题意,作出正棱台以及球的截面图,作辅助线结合圆的切线性质,求得球的半径,即可求得答案.
【解答】解:根据题意,设球O与上底面、下底面分别切于点O1,O2,与面ADD1A1,面BCC1B1分别切于点E、F,
其截面如图所示:
则MO1=ME=1,EN=NO2=2,
于是,MN=1+2=3,
过点M作MH⊥O2N于点H,则NH=NO2﹣MO1=1,
由勾股定理可得:,
所以,
所以该四棱台的高是.
故答案为:.
【点评】本题考查圆台、球的结构特征,关键是作出圆台、球的轴截面,属于基础题.
12.(2024 沙依巴克区校级模拟)若正四棱台的上、下底面边长分别是5和7,对角线长为9,则该棱台的高为 3 .
【考点】棱台的结构特征.
【专题】转化思想;数形结合法;空间位置关系与距离;直观想象;运算求解.
【答案】见试题解答内容
【分析】利用正四棱台的对角面为等腰梯形,再根据条件即可求出结果.
【解答】解:由题意,正四棱台的对角面为等腰梯形,
其中上底长为5,下底长为7,对角线长为9,
则高为3.
故答案为:3.
【点评】本题考查棱台的结构特征,属基础题.
四.解答题(共3小题)
13.(2024春 秦都区校级月考)如图,在正四棱台ABCD﹣A1B1C1D1中,E,F,G,H分别为棱A1B1,B1C1,AB,BC的中点.证明:
(1)E,F,G,H四点共面;
(2)多面体EFB1﹣GBH是三棱台.
【考点】棱台的结构特征;平面的基本性质及推论.
【专题】转化思想;转化法;立体几何;运算求解.
【答案】(1)证明见解析;(2)证明见解析.
【分析】(1)作出辅助线,得到线线平行,得到四点共面;
(2)作出辅助线,得到四边形EFHG为梯形,延长GE、HF,则GE与HF必相交,不妨设EG∩FH=P,由点线面的关系得到P∈BB1,故GE,FH,B1B交于一点,由平面EFB1∥平面GBH,得到多面体EFB1﹣GBH是三棱台.
【解答】解:(1)证明:连接AC,A1C1,如图所示,
在正四棱台ABCD﹣A1B1C1D1中,A1C1∥AC,
∵E,F,G,H分别为棱A1B1,B1C1,AB,BC的中点,
∴EF∥A1C1,GH∥AC,∴EF∥GH,
∴E,F,G,H四点共面.
(2)证明:∵A1C1≠AC,∴EF≠GH,且EF∥GH,
∴四边形EFHG为梯形,
延长GE、HF,则GE与HF必相交,不妨设EG∩FH=P,
∵GE 平面AA1B1B,∴P∈平面AA1B1B,
∵HF 平面BB1C1C,∴P∈平面BB1C1C,
又∵平面AA1B1B∩平面BB1C1C=BB1,∴P∈BB1,
∴GE,FH,B1B交于一点,
又平面EFB1∥平面GBH,
∴多面体EFB1﹣GBH是三棱台.
【点评】本题考查几何体的结构特征,属于中档题.
14.(2020秋 蚌埠期末)一个正四棱台的高是17cm,上、下底面边长分别为4cm和16cm.求这个棱台的侧棱长和斜高.
【考点】棱台的结构特征.
【专题】数形结合;综合法;空间位置关系与距离.
【答案】见试题解答内容
【分析】设棱台的两底面的中心分别是O1、O,B1C1和BC的中点分别是E1和E,连接O1O、E1E、O1B1、OB、O1E1、OE,则四边形OBB1O1和OEE1O1都是直角梯形.由此能求出这个棱台的侧棱长和斜高.
【解答】解:如图所示,设棱台的两底面的中心分别是O1、O,B1C1和BC的中点分别是E1和E,
连接O1O、E1E、O1B1、OB、O1E1、OE,
则四边形OBB1O1和OEE1O1都是直角梯形.
∵A1B1=4 cm,AB=16 cm,
∴O1E1=2 cm,OE=8 cm,
O1B1=2 cm,OB=8 cm,
∴B1B2=O1O2+(OB﹣O1B1)2=361 cm2,
E1E2=O1O2+(OE﹣O1E1)2=325cm2,
∴B1B=19 cm,E1E=5cm.
∴这个棱台的侧棱长为19cm,斜高为5cm.
【点评】本题考查棱台的侧棱长和斜高的求法,是基础题,解题时要认真审题,注意正四棱台的结构特征的合理运用.
15.(2012秋 武城县校级月考)若一个正三棱台的两个底面的边长分别为1cm和7cm,侧棱长为5cm,求它的高和斜高.
【考点】棱台的结构特征.
【专题】空间位置关系与距离.
【答案】见试题解答内容
【分析】画出正三棱台的图形,连接上下底面中心,就是棱台的高,求出AE,利用勾股定理,求出A′E即可.在侧面等腰梯形中,计算出棱台的斜高的长度.
【解答】解:如图,设正三棱台的上下底的中心分别为O、O1,
连接上下底面中心OO1,
则AE2,AA′=5,
所以A′E=OO1,
即它的高为;
作出一个侧面等腰梯形的高,也是棱台的斜高,
则由等腰梯形的性质,
可得斜高h'4.
【点评】本题给出正三棱台棱台上下底面边长和侧棱长,求三棱台的高和斜高,着重考查了正棱台的结构特征,属于基础题.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
