【期末热点.重难点】棱锥(含解析)2024-2025学年人教A版(2019)数学高一下册
文档属性
| 名称 | 【期末热点.重难点】棱锥(含解析)2024-2025学年人教A版(2019)数学高一下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 16:55:49 | ||
图片预览




文档简介
期末热点.重难点 棱锥
一.选择题(共5小题)
1.(2025 濮阳一模)截交线,是平面与空间形体表面的交线,它是画法几何研究的内容之一.当空间形体表面是曲面时,截交线是一条平面曲线;当空间形体表面由若干个平面组成时,截交线是一个多边形.已知正三棱锥O﹣ABC,满足OA⊥OB,OB⊥OC,OA⊥OC,OA=3,点P在△ABC内部(含边界)运动,且,则点P的轨迹与这个正三棱锥的截交线长度为( )
A. B. C. D.π
2.(2024秋 新余校级月考)现有一三棱锥P﹣ABC,,O为其外接球(四个顶点均在球的球面上)球心,PC=PB,,平面PCB恰好经过点O.设平面ABC截球O的截面为α,截面中心为O′,若,O′A=4,G为α上一点,则PG取最大值时,tan∠PGO′=( )
A. B. C. D.
3.(2024 包河区校级学业考试)在三棱锥P﹣ABC中,PO⊥平面ABC,垂足为O,且PA=PB=PC,则点O一定是△ABC的( )
A.内心 B.外心 C.重心 D.垂心
4.(2024 东莞市校级模拟)若半径为r的小球可以在棱长均为8的四棱锥内部自由转动,则r的最大值为( )
A. B. C. D.
5.(2023秋 浦东新区校级期末)设A1,B1,C1,D1分别是四棱锥P﹣ABCD侧棱PA,PB,PC,PD上的点.给出以下两个命题,则( )
①若ABCD是平行四边形,但不是菱形,则A1B1C1D1可能是菱形;
②若ABCD不是平行四边形,则A1B1C1D1可能是平行四边形.
A.①真②真 B.①真②假 C.①假②真 D.①假②假
二.多选题(共5小题)
(多选)6.(2024 魏都区校级三模)已知三棱锥V﹣ABC,VA=VB=VC,△ABC是边长为2的正三角形,D,E别是VA,AB的中点,∠CDE=90°,V在平面ABC内的投影为点M,M在平面VAB内的投影为点P.则( )
A.VA,VB,VC两两垂直
B.P在平面VAC的投影为VA的中点
C.C,M,E三点共线
D.形如三棱锥V﹣ABC的容器能被整体装人一个直径为2.5的球
(多选)7.(2024春 神木市校级期末)如图,正三棱锥P﹣ABC和正三棱锥Q﹣ABC的侧棱长分别为2,,直线PQ与底面ABC相交于点O,OP=2OQ,则( )
A.
B.AQ,BQ,CQ两两垂直
C.AP与CQ的夹角为45°
D.点P,A,B,C,Q不可能同时在某个球的表面上
(多选)8.(2023春 江宁区校级期中)如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的正方形,S到A,B,C,D的距离都等于2.下列选项中,正确的是( )
A. B.
C. D.
(多选)9.(2023秋 宛城区校级月考)如图,有一个正四面体形状的木块,其棱长为a.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
A.过棱AC的截面中,截面面积的最小值为
B.若过棱AC的截面与棱BD(不含端点)交于点P,则
C.若该木块的截面为平行四边形,则该截面面积的最大值为
D.与该木块各个顶点的距离都相等的截面有7个
(多选)10.(2023秋 朝阳期中)如图,有一个正四面体形状的木块,其棱长为a.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
A.过棱AC的截面中,截面面积的最小值为
B.若过棱AC的截面与棱BD(不含端点)交于点P,则cos∠APC的最小值为
C.若该木块的截面为平行四边形,则该截面面积的最大值为
D.与该木块各个顶点的距离都相等的截面有7个
三.填空题(共3小题)
11.(2024秋 闵行区期末)侧棱长为2的正三棱锥V﹣ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF,则截面△AEF周长的最小值为 .
12.(2024春 华池县校级期中)在四棱锥P﹣ABCD中,(4,﹣2,3),(﹣4,1,0),(﹣6,2,﹣8),则该四棱锥的高为 .
13.(2024 诸暨市三模)若正四面体ABCD的棱长为1,以三个侧面为底面向外作三个正四面体P1ABC,P2ABD,P3ACD,则△P1P2P3外接圆的半径是 .
四.解答题(共2小题)
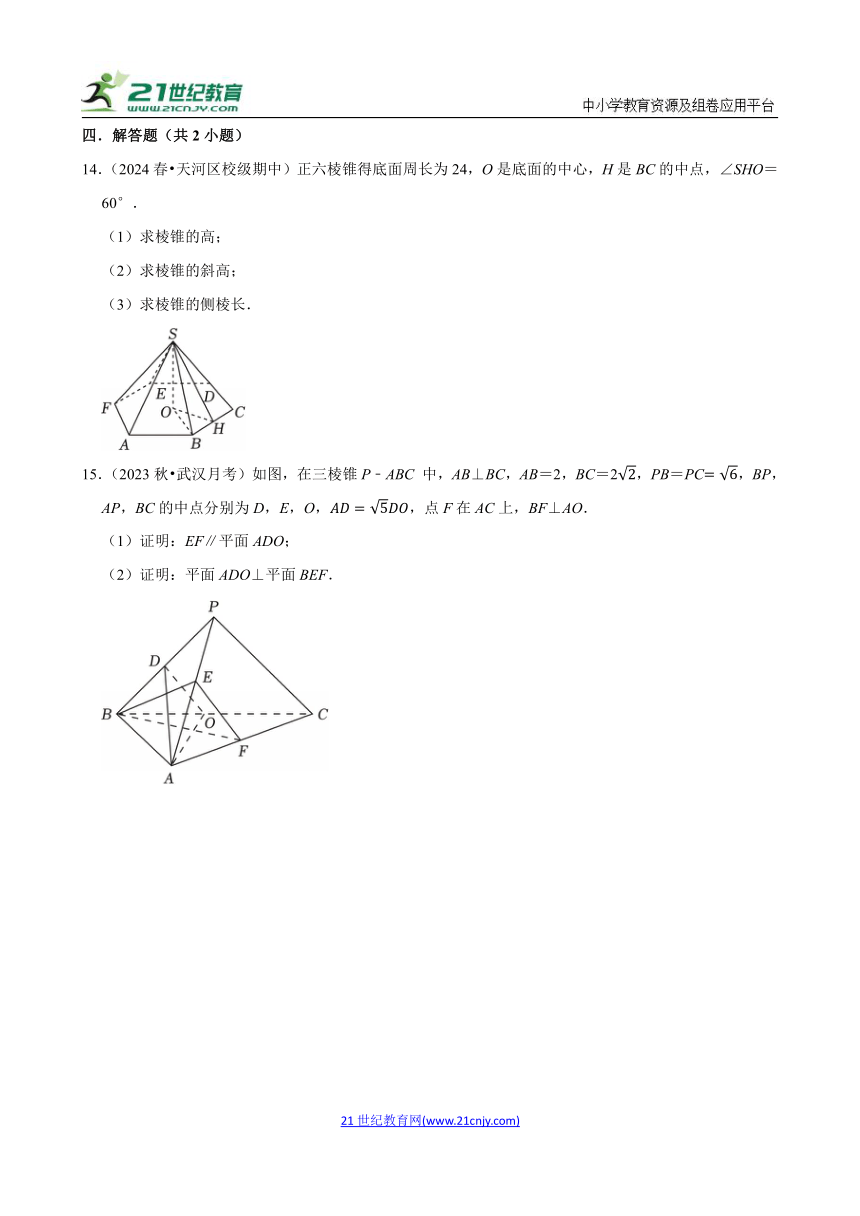
14.(2024春 天河区校级期中)正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.
(1)求棱锥的高;
(2)求棱锥的斜高;
(3)求棱锥的侧棱长.
15.(2023秋 武汉月考)如图,在三棱锥P﹣ABC 中,AB⊥BC,AB=2,BC=2,PB=PC,BP,AP,BC的中点分别为D,E,O,,点F在AC上,BF⊥AO.
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF.
期末热点.重难点 棱锥
参考答案与试题解析
一.选择题(共5小题)
1.(2025 濮阳一模)截交线,是平面与空间形体表面的交线,它是画法几何研究的内容之一.当空间形体表面是曲面时,截交线是一条平面曲线;当空间形体表面由若干个平面组成时,截交线是一个多边形.已知正三棱锥O﹣ABC,满足OA⊥OB,OB⊥OC,OA⊥OC,OA=3,点P在△ABC内部(含边界)运动,且,则点P的轨迹与这个正三棱锥的截交线长度为( )
A. B. C. D.π
【考点】棱锥的结构特征.
【专题】转化思想;转化法;立体几何;运算求解.
【答案】A
【分析】由题意可得,所以点P的轨迹是以O为球心,半径为的球面与△ABC内部(含边界)包含的平面相交所得的弧,即点P的轨迹是以正△ABC的中心E为圆心,为半径的圆在△ABC内部 (含边界)的弧,在平面图形中求出弧长即可.
【解答】解:由题意可知,正三棱锥O﹣ABC,满足OA⊥OB,OB⊥OC,OA⊥OC,OA=3,
可得OA⊥平面OBC,得底面正△ABC的边长为,设正△ABC的中心为E,
由V三棱锥O﹣ABC=V三棱锥A﹣OBC,
得,
解得,
又,
点P在△ABC内部(含边界)运动,且,
所以点P的轨迹是以O为球心,半径为的球面与△ABC内部(含边界)包含的平面相交所得的弧,
即点P的轨迹是以E为圆心,为半径的圆在△ABC内部(含边界)的弧,
如图,作ED⊥AB于D,圆与AB交点为G、H,则,
,
所以,则,所以,
则点P的轨迹在△ABC内部(含边界)的弧所对的圆心角为,
则弧长为,
即点P的轨迹与这个正三棱锥的截交线长度为.
故选:A.
【点评】本题考查立体几何中动点轨迹问题,属于难题.
2.(2024秋 新余校级月考)现有一三棱锥P﹣ABC,,O为其外接球(四个顶点均在球的球面上)球心,PC=PB,,平面PCB恰好经过点O.设平面ABC截球O的截面为α,截面中心为O′,若,O′A=4,G为α上一点,则PG取最大值时,tan∠PGO′=( )
A. B. C. D.
【考点】棱锥的结构特征.
【专题】分类讨论;数形结合法;立体几何;运算求解;空间想象.
【答案】D
【分析】解出三角形ABC,再应用球的截面性质求出球的半径,根据三角形PCB的等腰特点确定点P的位置并求出点P到截面的距离,分析当PG取最大值时,需P′G取到最大值,进而求解tan∠PGO′.
【解答】解:∵在截面α内 0,∴AC⊥BC,
即△ABC为直角三角形,所以截面中心O′为AB中点.
∵O′为截面中心,由球的截面性质可知,OO′⊥截面α,
又AB 截面α,∴OO′⊥AB.
在Rt△OO′A中,tan∠OAB,O′A=4,
∴OO′=3,OA=5,OB=OC=OP=5,
取BC的中点M,连MP,
∵平面PCB恰好经过点O,∴点O为三角形PCB的外心,
又∵PC=PB,∴MP⊥BC,且O,P,M三点共线,
当点O在三角形PCB内部时(如图1所示),作PP′⊥α,垂足为点P′,
∴PP′∥OO′,且点P′,点O′,点M三点共线,连MP′.
在Rt△ABC中,AC⊥BC,AB=2O′A=8,CA=2,∴BC=6,
在Rt△BMO中,OM⊥BM,OB=5,,∴OM=4,
在Rt△PP′M中,OO′∥PP′,OP=5,OM=4,OO′=3,
根据相似知识知,PP′,O′P′,
∴PG,
又∵G为α上一点,∴P′Gmax=O′P′+44时,PG才取最大值,
此时tan∠PGO′.
当点O在三角形PCB外部时(如图2所示),同理可得PP′,O′P′,
∴当,PG取最大值,
而此时 .
综上,PG取最大值时,.
故选:D.
【点评】本题考查了棱锥的结构特征与应用问题,也考查了运算求解与空间想象能力,是中档题.
3.(2024 包河区校级学业考试)在三棱锥P﹣ABC中,PO⊥平面ABC,垂足为O,且PA=PB=PC,则点O一定是△ABC的( )
A.内心 B.外心 C.重心 D.垂心
【考点】棱锥的结构特征.
【专题】对应思想;定义法;立体几何;逻辑思维.
【答案】B
【分析】由题意知,三条斜线在底面的射影相等,即此点到底面三角形三个顶点的距离相等,由此得出该点是三角形的外心.
【解答】解:由题意点P为△ABC所在平面外一点,PO⊥平面ABC,垂足为O,
若PA=PB=PC,则它们在底面上的射影也相等,
由此知点O到△ABC的三个顶点的距离相等,
由外心的定义知,点O是三角形的外心.
故选:B.
【点评】本题考查了三角形的外心定义与判断问题,解题的关键是根据题设条件得出PA,PB,PC在底面上的射影相等,是基础题.
4.(2024 东莞市校级模拟)若半径为r的小球可以在棱长均为8的四棱锥内部自由转动,则r的最大值为( )
A. B. C. D.
【考点】棱锥的结构特征.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】C
【分析】根据内切球半径满足的条件,将其放在三角形中,通过已知条件列方程,结合解三角形知识即可求解.
【解答】解:根据题意,设该四棱锥为四棱锥S﹣ABCD,如图:
连接AC,BD,交于点M,连接SM,则该四棱锥的内切球球心O在线段SM上.
设内切球与侧面SBC相切于点N,球O的半径为r0,连接ON,
则ON⊥平面SBC,且OM=ON=r0.
连接SN并延长,交BC于点E,连接ME,
则E为BC的中点,SE⊥BC,ME⊥BC.
由四棱锥的棱长均为8,可知,ME=4,.
易知△SON∽△SEM,
所以,
即,得,故r的最大值为.
故选:C.
【点评】本题考查棱锥的结构特征,涉及棱锥的内切球的问题,属于中档题.
5.(2023秋 浦东新区校级期末)设A1,B1,C1,D1分别是四棱锥P﹣ABCD侧棱PA,PB,PC,PD上的点.给出以下两个命题,则( )
①若ABCD是平行四边形,但不是菱形,则A1B1C1D1可能是菱形;
②若ABCD不是平行四边形,则A1B1C1D1可能是平行四边形.
A.①真②真 B.①真②假 C.①假②真 D.①假②假
【考点】棱锥的结构特征.
【专题】转化思想;定义法;简易逻辑;直观想象.
【答案】C
【分析】对于②,可以考虑构造一个正四棱锥来说明,对于①可以考虑利用反证法证伪.
【解答】解:对于②,考虑一个正四棱锥,然后再他的侧棱的延长线上可以画出一个梯形,
具体做法是:取PA1=PB1=PC1=PD1,则四棱锥P﹣A1B1C1D1为正四棱锥,
然后令PA=2PA1,PB=2PB1,PC=3PC1,PD=3PD1;
那么AD∥BC,AD≠BC,
此时ABCD是梯形,但不是平行四边形,
对于①,如图,四边形ABCD为平行四边形,A1B1C1D1 也为平行四边形,
若平面ABCD与平面A1B1C1D1 不平行,
则四边形A1B1C1D1 中必有一边与底面ABCD相交,
不妨设直线A1D1 与底面相交,则直线B1C1 也与底面相交,
在平面PAD中过P做A1D1 的平行线,交AD与T,则PT∥B1C1,
因P∈平面PBC,B1C1 平面PBC,故PT 平面PBC,即T∈平面PBC,
而平面PBC∩平面ABCD=BC,故T∈BC,而T∈AD,
故BC,AD相交,这与ABCD为平行四边形矛盾,
故平面ABCD∥平面A1B1C1D1,故,
若四边形A1B1C1D1 为菱形,则A1B1=A1D1,则AB=AD,
故四边形ABCD为菱形,故①错误.
故选:C.
【点评】本题考查命题的真值判断,属于中档题.
二.多选题(共5小题)
(多选)6.(2024 魏都区校级三模)已知三棱锥V﹣ABC,VA=VB=VC,△ABC是边长为2的正三角形,D,E别是VA,AB的中点,∠CDE=90°,V在平面ABC内的投影为点M,M在平面VAB内的投影为点P.则( )
A.VA,VB,VC两两垂直
B.P在平面VAC的投影为VA的中点
C.C,M,E三点共线
D.形如三棱锥V﹣ABC的容器能被整体装人一个直径为2.5的球
【考点】棱锥的结构特征;平行投影及平行投影作图法.
【专题】整体思想;综合法;空间位置关系与距离;直观想象.
【答案】ACD
【分析】A选项,作出辅助线,得到VB⊥平面VAC,结合勾股定理逆定理得到三条侧棱两两垂直;B选项,作出辅助线,得到P在平面VAC的投影不为VA的中点;C选项,根据正三棱锥的特征得到三点共线;D选项,求出三棱锥V﹣ABC 的外接球直径,与2.5比较后得到答案.
【解答】解:A选项,因为D,E分别为VA,AB的中点,所以DE∥VB,因为∠CDE=90°,
所以CD⊥DE,故CD⊥VB,
取AC的中点S,连接VS,BS,因为VA=VC,AB=BC,所以VS⊥AC,BS⊥AC,又VS∩BS=S,VS,BS 平面VBS,
所以AC⊥平面VBS,因为VB 平面VBS,所以AC⊥VB,因为CD∩AC=C,CD,AC 平面VAC,
所以VB⊥平面VAC,因为VA,VC 平面VAC,
所以VB⊥VA,VB⊥VC,又VA=VB=VC,AB=BC=2,故 又AC=2,VA2+VC2=AC2,
由勾股定理逆定理得VA⊥VC,VA,VB,VC两两垂直,A正确;
B选项,由题意得E,P不重合,过点P作PW∥VB,交VA于点W,因为VB⊥平面VAC,
所以PW⊥平面VAC,且W,D不重合,故P在平面VAC的投影不为VA的中点,B错误;
C选项,三棱锥V﹣ABC为正三棱锥,故点M为等边三角形ABC的中心,故C,M,E三点共线,C正确;
D选项,因为VA,VB,VC两两垂直,故三棱锥V﹣ABC的外接球即为以VA,VB,VC为棱的正方体的外接球,
故外接球直径为 ,而,
形如三棱锥V﹣ABC的容器能被整体装入一个直径为2.5的球,D正确.
故选:ACD.
【点评】本题主要考查了垂直及平行关系的判断及性质的应用,还考查了几何体性质的应用,考查了空间想象能力的应用,属于中档题.
(多选)7.(2024春 神木市校级期末)如图,正三棱锥P﹣ABC和正三棱锥Q﹣ABC的侧棱长分别为2,,直线PQ与底面ABC相交于点O,OP=2OQ,则( )
A.
B.AQ,BQ,CQ两两垂直
C.AP与CQ的夹角为45°
D.点P,A,B,C,Q不可能同时在某个球的表面上
【考点】棱锥的结构特征;异面直线及其所成的角;点、线、面间的距离计算.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】BC
【分析】根据题意,结合正三棱锥的特征,利用顶点在底面的投影是底面的中心可分析A与B,利用割补法可分析C与D,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于A选项,由正三棱锥的性质知PQ⊥平面ABC,
如图,连接OA,可得PQ⊥OA,有,
有,解得,
可得,故A选项错误;
对于B选项,由,
可得,又由,
可得,
易知AQ,BQ,CQ两两垂直,故B选项正确;
对于C选项,由AQ,BQ,CQ两两垂直,AB=BC=AC=AP=BP=CP=2,
把正三棱锥P﹣ABC和正三棱锥Q﹣ABC拼成的几何体放入如图所示正方体中,
可知AP与CQ的夹角为45°,故C选项正确;
对于D选项,由C选项知,点P,A,B,C,Q可以同时在以PQ为直径的球上,故D选项错误.
故选:BC.
【点评】本题考查棱锥的结构特征,涉及空间点线面距离的计算,属于中档题.
(多选)8.(2023春 江宁区校级期中)如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的正方形,S到A,B,C,D的距离都等于2.下列选项中,正确的是( )
A. B.
C. D.
【考点】棱锥的结构特征.
【专题】转化思想;转化法;立体几何;逻辑思维.
【答案】CD
【分析】利用空间向量的线性运算判断选项A,B,C,利用空间向量数量积的定义结合三棱锥的几何性质判断选项D,即可得到答案.
【解答】解:因为,
故选项C正确,选项A错误;
因为,
故选项B错误;
因为底面ABCD是边长为1的正方形,S到A,B,C,D的距离都等于2,
则,
,
因为∠ASB=∠CSD,
所以,故选项D正确.
故选:CD.
【点评】本题考查了空间向量的线性运算,空间向量数量积定义的理解与应用,三棱锥几何性质的理解与应用,考查了逻辑推理能力与化简运算能力,属于基础题.
(多选)9.(2023秋 宛城区校级月考)如图,有一个正四面体形状的木块,其棱长为a.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
A.过棱AC的截面中,截面面积的最小值为
B.若过棱AC的截面与棱BD(不含端点)交于点P,则
C.若该木块的截面为平行四边形,则该截面面积的最大值为
D.与该木块各个顶点的距离都相等的截面有7个
【考点】棱锥的结构特征;平面的基本性质及推论;命题的真假判断与应用.
【专题】计算题;转化思想;综合法;空间位置关系与距离;运算求解.
【答案】ACD
【分析】根据题意,利用余弦定理、三角形面积公式与三角函数的值域,验证A、B两项的正误;根据矩形的面积公式与二次函数的性质,验证C的正误;根据线面平行的性质与点到平面的距离,验证D的正误,即可得到本题的答案.
【解答】解:对于A,设截面与棱BD的交点为P,如图1,过棱AC的截面为△ACP,
当P为棱BD的中点时,△ACP的面积取得最小值,
△APC中,AC=a,,,,
故△ACP的面积最小值,A正确.
对于B,设AP=CP=t,,,
在△ACP中,,所以,B错误.
对于C,如图2,当截面EFNM为平行四边形时,EF∥MN,EM∥FN.
由AD⊥BC,可得EM⊥MN,所以平行四边形EFNM为长方形.
设EM=x,则MN=a﹣x,所以长方形EFNM的面积S,当且仅当时,等号成立,C正确.
对于D,与该木块各个顶点的距离都相等的截面分为以下两类:
第一类:平行于正四面体的一个面,且到顶点和到底面距离相等,这样的截面有4个.
第二类:平行于正四面体的两条对棱,且到两条棱距离相等,这样的截面有3个.
故与该木块各个顶点的距离都相等的截面共有7个,D正确.
故答案为:ACD.
【点评】本题主要考查空间位置关系与距离、正余弦定理及其应用、求函数的值域与最值等知识,考查了几何图形的理解能力与逻辑推理能力,属于中档题.
(多选)10.(2023秋 朝阳期中)如图,有一个正四面体形状的木块,其棱长为a.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
A.过棱AC的截面中,截面面积的最小值为
B.若过棱AC的截面与棱BD(不含端点)交于点P,则cos∠APC的最小值为
C.若该木块的截面为平行四边形,则该截面面积的最大值为
D.与该木块各个顶点的距离都相等的截面有7个
【考点】棱锥的结构特征;平面的基本性质及推论.
【专题】整体思想;综合法;立体几何;直观想象;运算求解.
【答案】ABD
【分析】对于A,当过棱AC的截面过棱BD的中点时,截面面积最小,求出其面积即可;对于B,利用余弦定理求解;对于C,当截面EFNM为平行四边形时,可得平行四边形EFNM为长方形,设EM=x,则MN=a﹣x,所以长方形EFNM的面积S=x(a﹣x),再利用基本不等式求解即可;对于D,分平行于正四面体的一个面,且到顶点和到底面距离相等和平行于正四面体的两条对棱,且到两条棱距离相等两种情况讨论求解.
【解答】解:设截面与棱BD的交点为P,如图1,
过棱AC的截面为△ACP,当P为棱BD的中点时,△ACP的面积取得最小值,
此时AP=CPa,AC=a,
所以△ACP的面积为,
即截面面积的最小值为,故A正确;
设AP=CP=t,则,,
在△ACP中,,
所以,故B正确;
如图2,当截面EFNM为平行四边形时,EF∥NM,EM∥FN,
由AD⊥BC,知EM⊥MN,
从而平行四边形EFNM为长方形,设EM=x,则MN=a﹣x,
所以长方形EFNM的面积S,当且仅当时,等号成立,故C错误;
与该木块各个顶点的距离都相等的截面分为两类,
第一类:平行于正四面体的一个面,且到顶点和到底面距离相等,这样的截面有4个,
第二类:平行于正四面体的两条对棱,且到两条棱距离相等,这样的截面有3个,
故与该木块各个顶点的距离都相等的截面共有7个,故D正确.
故选:ABD.
【点评】本题主要考查了正四面体的结构特征,考查了余弦定理的应用,以及基本不等式的应用,属于中档题.
三.填空题(共3小题)
11.(2024秋 闵行区期末)侧棱长为2的正三棱锥V﹣ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF,则截面△AEF周长的最小值为 6 .
【考点】棱锥的结构特征.
【专题】空间位置关系与距离.
【答案】见试题解答内容
【分析】沿着侧棱VA把正三棱锥V﹣ABC展开在一个平面内,如图,则AA′即为截面△AEF周长的最小值,且∠AVA′=3×40=120°.△VAA′中,由余弦定理可得 AA'的值.
【解答】解:如图所示:沿着侧棱VA把正三棱锥V﹣ABC展开在一个平面内,如图(2),
则AA′即为截面△AEF周长的最小值,且∠AVA′=3×40=120°.
△VAA′中,由余弦定理可得 AA'6,
故答案为 6.
【点评】本题主要考查余弦定理的应用,棱锥的结构特征,利用棱锥的侧面展开图研究几条线段和的最小值问题,是一种重要的解题方法,属于基础题.
12.(2024春 华池县校级期中)在四棱锥P﹣ABCD中,(4,﹣2,3),(﹣4,1,0),(﹣6,2,﹣8),则该四棱锥的高为 2 .
【考点】棱锥的结构特征.
【专题】转化思想;向量法;立体几何.
【答案】见试题解答内容
【分析】求出平面ABCD的法向量,然后利用点到平面的距离公式求解即可.
【解答】解:四棱锥P﹣ABCD中,(4,﹣2,3),(﹣4,1,0),(﹣6,2,﹣8),
设平面ABCD的法向量为(x,y,z),
则,
可得,
不妨令x=3,则y=12,z=4,
可得(3,12,4);
则(﹣6,2,﹣8)在平面ABCD上的射影就是这个四棱锥的高h,
所以h=|||cos,|=||2;
所以该四棱锥的高为2.
故答案为:2.
【点评】本题考查空间点到平面的距离公式的应用,向量的数量积的应用,考查计算能力.
13.(2024 诸暨市三模)若正四面体ABCD的棱长为1,以三个侧面为底面向外作三个正四面体P1ABC,P2ABD,P3ACD,则△P1P2P3外接圆的半径是 .
【考点】棱锥的结构特征.
【专题】转化思想;综合法;立体几何;运算求解.
【答案】.
【分析】将正四面体ABCD放置在正方体中,得到相应顶点坐标,进而求得P1,P2的坐标,求得线段|P1P2|,从而得出外接圆半径.
【解答】解:不妨将此正四面体ABCD放置在正方体中,
从而可得A(0,0,0),,,,
则△ABC的中心为 ,且此中心为P1D的中点,则;
同样△ABD的中心为,且此中心为P2C的中点,则,
∴,
∴△P1P2P3外接圆的半径是.
故答案为:.
【点评】本题考查棱锥的结构特征,考查中点坐标公式及三角形外接圆半径求法,属中档题.
四.解答题(共2小题)
14.(2024春 天河区校级期中)正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.
(1)求棱锥的高;
(2)求棱锥的斜高;
(3)求棱锥的侧棱长.
【考点】棱锥的结构特征.
【专题】计算题;数形结合;数形结合法;空间位置关系与距离.
【答案】见试题解答内容
【分析】先求出正六棱锥的底面边长为4,OHBC=2,由此利用直角三角形的性质能求出棱锥的高、斜高和侧棱长.
【解答】解:(1)∵正六棱锥的底面周长为24,∴正六棱锥的底面边长为4.
在正棱锥S﹣ABCDEF中,取BC的中点H,连结SH,SH⊥BC,O是正六边形ABCDEF的中心.
连结SO,则SO⊥底面ABCDEF.
在Rt△SOH中,OHBC=2,
∴∠SHO=60°,∴棱锥的高SO=OH tAn60°=6.
(2)在△SOH中,∵∠SHO=60°,SO⊥OH,
∴棱锥的斜高SH=2OH=4.
(3)Rt△SOH中,∵SO=6,OB=BC=4,SO⊥OH,
∴棱锥的侧棱长SB2.
【点评】本题考查棱锥的高、斜高和侧棱长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.
15.(2023秋 武汉月考)如图,在三棱锥P﹣ABC 中,AB⊥BC,AB=2,BC=2,PB=PC,BP,AP,BC的中点分别为D,E,O,,点F在AC上,BF⊥AO.
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF.
【考点】棱锥的结构特征.
【专题】数形结合;定义法;立体几何;直观想象;运算求解.
【答案】(1)证明过程见解析;(2)证明过程见解析.
【分析】(1)利用向量法可得OF∥AB,OFAB,四边形ODEF为平行四边形,根据线面平行的判定定理即可证明;
(2)由勾股定理可得AO⊥OD,AO⊥EF,根据面面垂直的判定定理即可证明.
【解答】证明:(1)由题可知,||=2,设λ,
∵cos∠BAC=4,
则() ()()8λ﹣4=0,解得,
∴OF∥AB,OFAB,
而DE∥AB,DEAB,∴DE∥OF,DE=OF,∴四边形ODEF为平行四边形,
∴EF∥OD,
∵OD 平面ADO,EF 平面ADO,
∴EF∥平面ADO.
(2)AOPC=2OD,ADOD,
∴AD2=AO2+OD2,即AO⊥OD,AO⊥EF,
∵BF⊥AO,BF∩EF=F,
∴AO⊥平面BEF,
∵AO 平面ADO,
∴平面ADO⊥平面BEF.
【点评】本题考查直线与平面、平面与平面位置关系的判定定理,是中档题.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2025 濮阳一模)截交线,是平面与空间形体表面的交线,它是画法几何研究的内容之一.当空间形体表面是曲面时,截交线是一条平面曲线;当空间形体表面由若干个平面组成时,截交线是一个多边形.已知正三棱锥O﹣ABC,满足OA⊥OB,OB⊥OC,OA⊥OC,OA=3,点P在△ABC内部(含边界)运动,且,则点P的轨迹与这个正三棱锥的截交线长度为( )
A. B. C. D.π
2.(2024秋 新余校级月考)现有一三棱锥P﹣ABC,,O为其外接球(四个顶点均在球的球面上)球心,PC=PB,,平面PCB恰好经过点O.设平面ABC截球O的截面为α,截面中心为O′,若,O′A=4,G为α上一点,则PG取最大值时,tan∠PGO′=( )
A. B. C. D.
3.(2024 包河区校级学业考试)在三棱锥P﹣ABC中,PO⊥平面ABC,垂足为O,且PA=PB=PC,则点O一定是△ABC的( )
A.内心 B.外心 C.重心 D.垂心
4.(2024 东莞市校级模拟)若半径为r的小球可以在棱长均为8的四棱锥内部自由转动,则r的最大值为( )
A. B. C. D.
5.(2023秋 浦东新区校级期末)设A1,B1,C1,D1分别是四棱锥P﹣ABCD侧棱PA,PB,PC,PD上的点.给出以下两个命题,则( )
①若ABCD是平行四边形,但不是菱形,则A1B1C1D1可能是菱形;
②若ABCD不是平行四边形,则A1B1C1D1可能是平行四边形.
A.①真②真 B.①真②假 C.①假②真 D.①假②假
二.多选题(共5小题)
(多选)6.(2024 魏都区校级三模)已知三棱锥V﹣ABC,VA=VB=VC,△ABC是边长为2的正三角形,D,E别是VA,AB的中点,∠CDE=90°,V在平面ABC内的投影为点M,M在平面VAB内的投影为点P.则( )
A.VA,VB,VC两两垂直
B.P在平面VAC的投影为VA的中点
C.C,M,E三点共线
D.形如三棱锥V﹣ABC的容器能被整体装人一个直径为2.5的球
(多选)7.(2024春 神木市校级期末)如图,正三棱锥P﹣ABC和正三棱锥Q﹣ABC的侧棱长分别为2,,直线PQ与底面ABC相交于点O,OP=2OQ,则( )
A.
B.AQ,BQ,CQ两两垂直
C.AP与CQ的夹角为45°
D.点P,A,B,C,Q不可能同时在某个球的表面上
(多选)8.(2023春 江宁区校级期中)如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的正方形,S到A,B,C,D的距离都等于2.下列选项中,正确的是( )
A. B.
C. D.
(多选)9.(2023秋 宛城区校级月考)如图,有一个正四面体形状的木块,其棱长为a.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
A.过棱AC的截面中,截面面积的最小值为
B.若过棱AC的截面与棱BD(不含端点)交于点P,则
C.若该木块的截面为平行四边形,则该截面面积的最大值为
D.与该木块各个顶点的距离都相等的截面有7个
(多选)10.(2023秋 朝阳期中)如图,有一个正四面体形状的木块,其棱长为a.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
A.过棱AC的截面中,截面面积的最小值为
B.若过棱AC的截面与棱BD(不含端点)交于点P,则cos∠APC的最小值为
C.若该木块的截面为平行四边形,则该截面面积的最大值为
D.与该木块各个顶点的距离都相等的截面有7个
三.填空题(共3小题)
11.(2024秋 闵行区期末)侧棱长为2的正三棱锥V﹣ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF,则截面△AEF周长的最小值为 .
12.(2024春 华池县校级期中)在四棱锥P﹣ABCD中,(4,﹣2,3),(﹣4,1,0),(﹣6,2,﹣8),则该四棱锥的高为 .
13.(2024 诸暨市三模)若正四面体ABCD的棱长为1,以三个侧面为底面向外作三个正四面体P1ABC,P2ABD,P3ACD,则△P1P2P3外接圆的半径是 .
四.解答题(共2小题)
14.(2024春 天河区校级期中)正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.
(1)求棱锥的高;
(2)求棱锥的斜高;
(3)求棱锥的侧棱长.
15.(2023秋 武汉月考)如图,在三棱锥P﹣ABC 中,AB⊥BC,AB=2,BC=2,PB=PC,BP,AP,BC的中点分别为D,E,O,,点F在AC上,BF⊥AO.
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF.
期末热点.重难点 棱锥
参考答案与试题解析
一.选择题(共5小题)
1.(2025 濮阳一模)截交线,是平面与空间形体表面的交线,它是画法几何研究的内容之一.当空间形体表面是曲面时,截交线是一条平面曲线;当空间形体表面由若干个平面组成时,截交线是一个多边形.已知正三棱锥O﹣ABC,满足OA⊥OB,OB⊥OC,OA⊥OC,OA=3,点P在△ABC内部(含边界)运动,且,则点P的轨迹与这个正三棱锥的截交线长度为( )
A. B. C. D.π
【考点】棱锥的结构特征.
【专题】转化思想;转化法;立体几何;运算求解.
【答案】A
【分析】由题意可得,所以点P的轨迹是以O为球心,半径为的球面与△ABC内部(含边界)包含的平面相交所得的弧,即点P的轨迹是以正△ABC的中心E为圆心,为半径的圆在△ABC内部 (含边界)的弧,在平面图形中求出弧长即可.
【解答】解:由题意可知,正三棱锥O﹣ABC,满足OA⊥OB,OB⊥OC,OA⊥OC,OA=3,
可得OA⊥平面OBC,得底面正△ABC的边长为,设正△ABC的中心为E,
由V三棱锥O﹣ABC=V三棱锥A﹣OBC,
得,
解得,
又,
点P在△ABC内部(含边界)运动,且,
所以点P的轨迹是以O为球心,半径为的球面与△ABC内部(含边界)包含的平面相交所得的弧,
即点P的轨迹是以E为圆心,为半径的圆在△ABC内部(含边界)的弧,
如图,作ED⊥AB于D,圆与AB交点为G、H,则,
,
所以,则,所以,
则点P的轨迹在△ABC内部(含边界)的弧所对的圆心角为,
则弧长为,
即点P的轨迹与这个正三棱锥的截交线长度为.
故选:A.
【点评】本题考查立体几何中动点轨迹问题,属于难题.
2.(2024秋 新余校级月考)现有一三棱锥P﹣ABC,,O为其外接球(四个顶点均在球的球面上)球心,PC=PB,,平面PCB恰好经过点O.设平面ABC截球O的截面为α,截面中心为O′,若,O′A=4,G为α上一点,则PG取最大值时,tan∠PGO′=( )
A. B. C. D.
【考点】棱锥的结构特征.
【专题】分类讨论;数形结合法;立体几何;运算求解;空间想象.
【答案】D
【分析】解出三角形ABC,再应用球的截面性质求出球的半径,根据三角形PCB的等腰特点确定点P的位置并求出点P到截面的距离,分析当PG取最大值时,需P′G取到最大值,进而求解tan∠PGO′.
【解答】解:∵在截面α内 0,∴AC⊥BC,
即△ABC为直角三角形,所以截面中心O′为AB中点.
∵O′为截面中心,由球的截面性质可知,OO′⊥截面α,
又AB 截面α,∴OO′⊥AB.
在Rt△OO′A中,tan∠OAB,O′A=4,
∴OO′=3,OA=5,OB=OC=OP=5,
取BC的中点M,连MP,
∵平面PCB恰好经过点O,∴点O为三角形PCB的外心,
又∵PC=PB,∴MP⊥BC,且O,P,M三点共线,
当点O在三角形PCB内部时(如图1所示),作PP′⊥α,垂足为点P′,
∴PP′∥OO′,且点P′,点O′,点M三点共线,连MP′.
在Rt△ABC中,AC⊥BC,AB=2O′A=8,CA=2,∴BC=6,
在Rt△BMO中,OM⊥BM,OB=5,,∴OM=4,
在Rt△PP′M中,OO′∥PP′,OP=5,OM=4,OO′=3,
根据相似知识知,PP′,O′P′,
∴PG,
又∵G为α上一点,∴P′Gmax=O′P′+44时,PG才取最大值,
此时tan∠PGO′.
当点O在三角形PCB外部时(如图2所示),同理可得PP′,O′P′,
∴当,PG取最大值,
而此时 .
综上,PG取最大值时,.
故选:D.
【点评】本题考查了棱锥的结构特征与应用问题,也考查了运算求解与空间想象能力,是中档题.
3.(2024 包河区校级学业考试)在三棱锥P﹣ABC中,PO⊥平面ABC,垂足为O,且PA=PB=PC,则点O一定是△ABC的( )
A.内心 B.外心 C.重心 D.垂心
【考点】棱锥的结构特征.
【专题】对应思想;定义法;立体几何;逻辑思维.
【答案】B
【分析】由题意知,三条斜线在底面的射影相等,即此点到底面三角形三个顶点的距离相等,由此得出该点是三角形的外心.
【解答】解:由题意点P为△ABC所在平面外一点,PO⊥平面ABC,垂足为O,
若PA=PB=PC,则它们在底面上的射影也相等,
由此知点O到△ABC的三个顶点的距离相等,
由外心的定义知,点O是三角形的外心.
故选:B.
【点评】本题考查了三角形的外心定义与判断问题,解题的关键是根据题设条件得出PA,PB,PC在底面上的射影相等,是基础题.
4.(2024 东莞市校级模拟)若半径为r的小球可以在棱长均为8的四棱锥内部自由转动,则r的最大值为( )
A. B. C. D.
【考点】棱锥的结构特征.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】C
【分析】根据内切球半径满足的条件,将其放在三角形中,通过已知条件列方程,结合解三角形知识即可求解.
【解答】解:根据题意,设该四棱锥为四棱锥S﹣ABCD,如图:
连接AC,BD,交于点M,连接SM,则该四棱锥的内切球球心O在线段SM上.
设内切球与侧面SBC相切于点N,球O的半径为r0,连接ON,
则ON⊥平面SBC,且OM=ON=r0.
连接SN并延长,交BC于点E,连接ME,
则E为BC的中点,SE⊥BC,ME⊥BC.
由四棱锥的棱长均为8,可知,ME=4,.
易知△SON∽△SEM,
所以,
即,得,故r的最大值为.
故选:C.
【点评】本题考查棱锥的结构特征,涉及棱锥的内切球的问题,属于中档题.
5.(2023秋 浦东新区校级期末)设A1,B1,C1,D1分别是四棱锥P﹣ABCD侧棱PA,PB,PC,PD上的点.给出以下两个命题,则( )
①若ABCD是平行四边形,但不是菱形,则A1B1C1D1可能是菱形;
②若ABCD不是平行四边形,则A1B1C1D1可能是平行四边形.
A.①真②真 B.①真②假 C.①假②真 D.①假②假
【考点】棱锥的结构特征.
【专题】转化思想;定义法;简易逻辑;直观想象.
【答案】C
【分析】对于②,可以考虑构造一个正四棱锥来说明,对于①可以考虑利用反证法证伪.
【解答】解:对于②,考虑一个正四棱锥,然后再他的侧棱的延长线上可以画出一个梯形,
具体做法是:取PA1=PB1=PC1=PD1,则四棱锥P﹣A1B1C1D1为正四棱锥,
然后令PA=2PA1,PB=2PB1,PC=3PC1,PD=3PD1;
那么AD∥BC,AD≠BC,
此时ABCD是梯形,但不是平行四边形,
对于①,如图,四边形ABCD为平行四边形,A1B1C1D1 也为平行四边形,
若平面ABCD与平面A1B1C1D1 不平行,
则四边形A1B1C1D1 中必有一边与底面ABCD相交,
不妨设直线A1D1 与底面相交,则直线B1C1 也与底面相交,
在平面PAD中过P做A1D1 的平行线,交AD与T,则PT∥B1C1,
因P∈平面PBC,B1C1 平面PBC,故PT 平面PBC,即T∈平面PBC,
而平面PBC∩平面ABCD=BC,故T∈BC,而T∈AD,
故BC,AD相交,这与ABCD为平行四边形矛盾,
故平面ABCD∥平面A1B1C1D1,故,
若四边形A1B1C1D1 为菱形,则A1B1=A1D1,则AB=AD,
故四边形ABCD为菱形,故①错误.
故选:C.
【点评】本题考查命题的真值判断,属于中档题.
二.多选题(共5小题)
(多选)6.(2024 魏都区校级三模)已知三棱锥V﹣ABC,VA=VB=VC,△ABC是边长为2的正三角形,D,E别是VA,AB的中点,∠CDE=90°,V在平面ABC内的投影为点M,M在平面VAB内的投影为点P.则( )
A.VA,VB,VC两两垂直
B.P在平面VAC的投影为VA的中点
C.C,M,E三点共线
D.形如三棱锥V﹣ABC的容器能被整体装人一个直径为2.5的球
【考点】棱锥的结构特征;平行投影及平行投影作图法.
【专题】整体思想;综合法;空间位置关系与距离;直观想象.
【答案】ACD
【分析】A选项,作出辅助线,得到VB⊥平面VAC,结合勾股定理逆定理得到三条侧棱两两垂直;B选项,作出辅助线,得到P在平面VAC的投影不为VA的中点;C选项,根据正三棱锥的特征得到三点共线;D选项,求出三棱锥V﹣ABC 的外接球直径,与2.5比较后得到答案.
【解答】解:A选项,因为D,E分别为VA,AB的中点,所以DE∥VB,因为∠CDE=90°,
所以CD⊥DE,故CD⊥VB,
取AC的中点S,连接VS,BS,因为VA=VC,AB=BC,所以VS⊥AC,BS⊥AC,又VS∩BS=S,VS,BS 平面VBS,
所以AC⊥平面VBS,因为VB 平面VBS,所以AC⊥VB,因为CD∩AC=C,CD,AC 平面VAC,
所以VB⊥平面VAC,因为VA,VC 平面VAC,
所以VB⊥VA,VB⊥VC,又VA=VB=VC,AB=BC=2,故 又AC=2,VA2+VC2=AC2,
由勾股定理逆定理得VA⊥VC,VA,VB,VC两两垂直,A正确;
B选项,由题意得E,P不重合,过点P作PW∥VB,交VA于点W,因为VB⊥平面VAC,
所以PW⊥平面VAC,且W,D不重合,故P在平面VAC的投影不为VA的中点,B错误;
C选项,三棱锥V﹣ABC为正三棱锥,故点M为等边三角形ABC的中心,故C,M,E三点共线,C正确;
D选项,因为VA,VB,VC两两垂直,故三棱锥V﹣ABC的外接球即为以VA,VB,VC为棱的正方体的外接球,
故外接球直径为 ,而,
形如三棱锥V﹣ABC的容器能被整体装入一个直径为2.5的球,D正确.
故选:ACD.
【点评】本题主要考查了垂直及平行关系的判断及性质的应用,还考查了几何体性质的应用,考查了空间想象能力的应用,属于中档题.
(多选)7.(2024春 神木市校级期末)如图,正三棱锥P﹣ABC和正三棱锥Q﹣ABC的侧棱长分别为2,,直线PQ与底面ABC相交于点O,OP=2OQ,则( )
A.
B.AQ,BQ,CQ两两垂直
C.AP与CQ的夹角为45°
D.点P,A,B,C,Q不可能同时在某个球的表面上
【考点】棱锥的结构特征;异面直线及其所成的角;点、线、面间的距离计算.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】BC
【分析】根据题意,结合正三棱锥的特征,利用顶点在底面的投影是底面的中心可分析A与B,利用割补法可分析C与D,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于A选项,由正三棱锥的性质知PQ⊥平面ABC,
如图,连接OA,可得PQ⊥OA,有,
有,解得,
可得,故A选项错误;
对于B选项,由,
可得,又由,
可得,
易知AQ,BQ,CQ两两垂直,故B选项正确;
对于C选项,由AQ,BQ,CQ两两垂直,AB=BC=AC=AP=BP=CP=2,
把正三棱锥P﹣ABC和正三棱锥Q﹣ABC拼成的几何体放入如图所示正方体中,
可知AP与CQ的夹角为45°,故C选项正确;
对于D选项,由C选项知,点P,A,B,C,Q可以同时在以PQ为直径的球上,故D选项错误.
故选:BC.
【点评】本题考查棱锥的结构特征,涉及空间点线面距离的计算,属于中档题.
(多选)8.(2023春 江宁区校级期中)如图,在四棱锥S﹣ABCD中,底面ABCD是边长为1的正方形,S到A,B,C,D的距离都等于2.下列选项中,正确的是( )
A. B.
C. D.
【考点】棱锥的结构特征.
【专题】转化思想;转化法;立体几何;逻辑思维.
【答案】CD
【分析】利用空间向量的线性运算判断选项A,B,C,利用空间向量数量积的定义结合三棱锥的几何性质判断选项D,即可得到答案.
【解答】解:因为,
故选项C正确,选项A错误;
因为,
故选项B错误;
因为底面ABCD是边长为1的正方形,S到A,B,C,D的距离都等于2,
则,
,
因为∠ASB=∠CSD,
所以,故选项D正确.
故选:CD.
【点评】本题考查了空间向量的线性运算,空间向量数量积定义的理解与应用,三棱锥几何性质的理解与应用,考查了逻辑推理能力与化简运算能力,属于基础题.
(多选)9.(2023秋 宛城区校级月考)如图,有一个正四面体形状的木块,其棱长为a.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
A.过棱AC的截面中,截面面积的最小值为
B.若过棱AC的截面与棱BD(不含端点)交于点P,则
C.若该木块的截面为平行四边形,则该截面面积的最大值为
D.与该木块各个顶点的距离都相等的截面有7个
【考点】棱锥的结构特征;平面的基本性质及推论;命题的真假判断与应用.
【专题】计算题;转化思想;综合法;空间位置关系与距离;运算求解.
【答案】ACD
【分析】根据题意,利用余弦定理、三角形面积公式与三角函数的值域,验证A、B两项的正误;根据矩形的面积公式与二次函数的性质,验证C的正误;根据线面平行的性质与点到平面的距离,验证D的正误,即可得到本题的答案.
【解答】解:对于A,设截面与棱BD的交点为P,如图1,过棱AC的截面为△ACP,
当P为棱BD的中点时,△ACP的面积取得最小值,
△APC中,AC=a,,,,
故△ACP的面积最小值,A正确.
对于B,设AP=CP=t,,,
在△ACP中,,所以,B错误.
对于C,如图2,当截面EFNM为平行四边形时,EF∥MN,EM∥FN.
由AD⊥BC,可得EM⊥MN,所以平行四边形EFNM为长方形.
设EM=x,则MN=a﹣x,所以长方形EFNM的面积S,当且仅当时,等号成立,C正确.
对于D,与该木块各个顶点的距离都相等的截面分为以下两类:
第一类:平行于正四面体的一个面,且到顶点和到底面距离相等,这样的截面有4个.
第二类:平行于正四面体的两条对棱,且到两条棱距离相等,这样的截面有3个.
故与该木块各个顶点的距离都相等的截面共有7个,D正确.
故答案为:ACD.
【点评】本题主要考查空间位置关系与距离、正余弦定理及其应用、求函数的值域与最值等知识,考查了几何图形的理解能力与逻辑推理能力,属于中档题.
(多选)10.(2023秋 朝阳期中)如图,有一个正四面体形状的木块,其棱长为a.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
A.过棱AC的截面中,截面面积的最小值为
B.若过棱AC的截面与棱BD(不含端点)交于点P,则cos∠APC的最小值为
C.若该木块的截面为平行四边形,则该截面面积的最大值为
D.与该木块各个顶点的距离都相等的截面有7个
【考点】棱锥的结构特征;平面的基本性质及推论.
【专题】整体思想;综合法;立体几何;直观想象;运算求解.
【答案】ABD
【分析】对于A,当过棱AC的截面过棱BD的中点时,截面面积最小,求出其面积即可;对于B,利用余弦定理求解;对于C,当截面EFNM为平行四边形时,可得平行四边形EFNM为长方形,设EM=x,则MN=a﹣x,所以长方形EFNM的面积S=x(a﹣x),再利用基本不等式求解即可;对于D,分平行于正四面体的一个面,且到顶点和到底面距离相等和平行于正四面体的两条对棱,且到两条棱距离相等两种情况讨论求解.
【解答】解:设截面与棱BD的交点为P,如图1,
过棱AC的截面为△ACP,当P为棱BD的中点时,△ACP的面积取得最小值,
此时AP=CPa,AC=a,
所以△ACP的面积为,
即截面面积的最小值为,故A正确;
设AP=CP=t,则,,
在△ACP中,,
所以,故B正确;
如图2,当截面EFNM为平行四边形时,EF∥NM,EM∥FN,
由AD⊥BC,知EM⊥MN,
从而平行四边形EFNM为长方形,设EM=x,则MN=a﹣x,
所以长方形EFNM的面积S,当且仅当时,等号成立,故C错误;
与该木块各个顶点的距离都相等的截面分为两类,
第一类:平行于正四面体的一个面,且到顶点和到底面距离相等,这样的截面有4个,
第二类:平行于正四面体的两条对棱,且到两条棱距离相等,这样的截面有3个,
故与该木块各个顶点的距离都相等的截面共有7个,故D正确.
故选:ABD.
【点评】本题主要考查了正四面体的结构特征,考查了余弦定理的应用,以及基本不等式的应用,属于中档题.
三.填空题(共3小题)
11.(2024秋 闵行区期末)侧棱长为2的正三棱锥V﹣ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF,则截面△AEF周长的最小值为 6 .
【考点】棱锥的结构特征.
【专题】空间位置关系与距离.
【答案】见试题解答内容
【分析】沿着侧棱VA把正三棱锥V﹣ABC展开在一个平面内,如图,则AA′即为截面△AEF周长的最小值,且∠AVA′=3×40=120°.△VAA′中,由余弦定理可得 AA'的值.
【解答】解:如图所示:沿着侧棱VA把正三棱锥V﹣ABC展开在一个平面内,如图(2),
则AA′即为截面△AEF周长的最小值,且∠AVA′=3×40=120°.
△VAA′中,由余弦定理可得 AA'6,
故答案为 6.
【点评】本题主要考查余弦定理的应用,棱锥的结构特征,利用棱锥的侧面展开图研究几条线段和的最小值问题,是一种重要的解题方法,属于基础题.
12.(2024春 华池县校级期中)在四棱锥P﹣ABCD中,(4,﹣2,3),(﹣4,1,0),(﹣6,2,﹣8),则该四棱锥的高为 2 .
【考点】棱锥的结构特征.
【专题】转化思想;向量法;立体几何.
【答案】见试题解答内容
【分析】求出平面ABCD的法向量,然后利用点到平面的距离公式求解即可.
【解答】解:四棱锥P﹣ABCD中,(4,﹣2,3),(﹣4,1,0),(﹣6,2,﹣8),
设平面ABCD的法向量为(x,y,z),
则,
可得,
不妨令x=3,则y=12,z=4,
可得(3,12,4);
则(﹣6,2,﹣8)在平面ABCD上的射影就是这个四棱锥的高h,
所以h=|||cos,|=||2;
所以该四棱锥的高为2.
故答案为:2.
【点评】本题考查空间点到平面的距离公式的应用,向量的数量积的应用,考查计算能力.
13.(2024 诸暨市三模)若正四面体ABCD的棱长为1,以三个侧面为底面向外作三个正四面体P1ABC,P2ABD,P3ACD,则△P1P2P3外接圆的半径是 .
【考点】棱锥的结构特征.
【专题】转化思想;综合法;立体几何;运算求解.
【答案】.
【分析】将正四面体ABCD放置在正方体中,得到相应顶点坐标,进而求得P1,P2的坐标,求得线段|P1P2|,从而得出外接圆半径.
【解答】解:不妨将此正四面体ABCD放置在正方体中,
从而可得A(0,0,0),,,,
则△ABC的中心为 ,且此中心为P1D的中点,则;
同样△ABD的中心为,且此中心为P2C的中点,则,
∴,
∴△P1P2P3外接圆的半径是.
故答案为:.
【点评】本题考查棱锥的结构特征,考查中点坐标公式及三角形外接圆半径求法,属中档题.
四.解答题(共2小题)
14.(2024春 天河区校级期中)正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.
(1)求棱锥的高;
(2)求棱锥的斜高;
(3)求棱锥的侧棱长.
【考点】棱锥的结构特征.
【专题】计算题;数形结合;数形结合法;空间位置关系与距离.
【答案】见试题解答内容
【分析】先求出正六棱锥的底面边长为4,OHBC=2,由此利用直角三角形的性质能求出棱锥的高、斜高和侧棱长.
【解答】解:(1)∵正六棱锥的底面周长为24,∴正六棱锥的底面边长为4.
在正棱锥S﹣ABCDEF中,取BC的中点H,连结SH,SH⊥BC,O是正六边形ABCDEF的中心.
连结SO,则SO⊥底面ABCDEF.
在Rt△SOH中,OHBC=2,
∴∠SHO=60°,∴棱锥的高SO=OH tAn60°=6.
(2)在△SOH中,∵∠SHO=60°,SO⊥OH,
∴棱锥的斜高SH=2OH=4.
(3)Rt△SOH中,∵SO=6,OB=BC=4,SO⊥OH,
∴棱锥的侧棱长SB2.
【点评】本题考查棱锥的高、斜高和侧棱长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.
15.(2023秋 武汉月考)如图,在三棱锥P﹣ABC 中,AB⊥BC,AB=2,BC=2,PB=PC,BP,AP,BC的中点分别为D,E,O,,点F在AC上,BF⊥AO.
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF.
【考点】棱锥的结构特征.
【专题】数形结合;定义法;立体几何;直观想象;运算求解.
【答案】(1)证明过程见解析;(2)证明过程见解析.
【分析】(1)利用向量法可得OF∥AB,OFAB,四边形ODEF为平行四边形,根据线面平行的判定定理即可证明;
(2)由勾股定理可得AO⊥OD,AO⊥EF,根据面面垂直的判定定理即可证明.
【解答】证明:(1)由题可知,||=2,设λ,
∵cos∠BAC=4,
则() ()()8λ﹣4=0,解得,
∴OF∥AB,OFAB,
而DE∥AB,DEAB,∴DE∥OF,DE=OF,∴四边形ODEF为平行四边形,
∴EF∥OD,
∵OD 平面ADO,EF 平面ADO,
∴EF∥平面ADO.
(2)AOPC=2OD,ADOD,
∴AD2=AO2+OD2,即AO⊥OD,AO⊥EF,
∵BF⊥AO,BF∩EF=F,
∴AO⊥平面BEF,
∵AO 平面ADO,
∴平面ADO⊥平面BEF.
【点评】本题考查直线与平面、平面与平面位置关系的判定定理,是中档题.
21世纪教育网(www.21cnjy.com)
同课章节目录
