【期末热点.重难点】频率与概率(含解析)2024-2025学年人教A版(2019)数学高一下册
文档属性
| 名称 | 【期末热点.重难点】频率与概率(含解析)2024-2025学年人教A版(2019)数学高一下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 00:00:00 | ||
图片预览




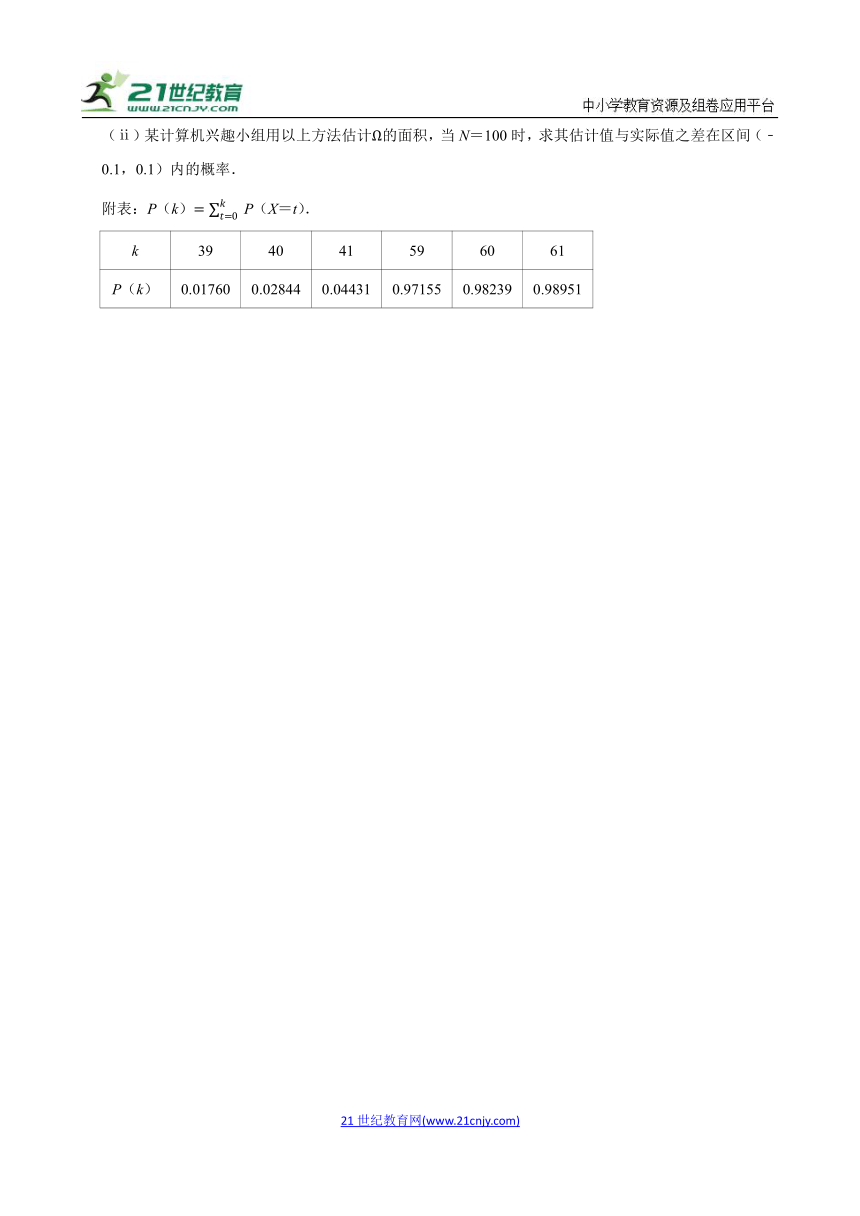
文档简介
期末热点.重难点 频率与概率
一.选择题(共5小题)
1.(2024秋 湖北期末)某学校乒乓球比赛,学生甲和学生乙比赛3局(采取三局两胜制),假设每局比赛甲获胜的概率是0.7,乙获胜的概率是0.3,利用计算机模拟试验,计算机产生0 9之间的随机数,当出现随机数0 6时,表示一局甲获胜,其概率是0.7.由于要比赛3局,所以每3个随机数为一组.例如,产生20组随机数:
603 099 316 696 851 916 062 107 493 977
329 906 355 860 375 107 347 467 822 166
根据随机数估计甲获胜的概率为( )
A.0.9 B.0.95 C.0.8 D.0.85
2.(2024秋 徐汇区校级期末)一个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.经过重复摸球足够多次试验后发现,摸到黑球的频率稳定在0.1左右,则据此估计盒子中红球的个数约为( )
A.40个 B.45个 C.50个 D.55个
3.(2024秋 高邮市月考)已知一批产品中有90%是合格品,检验产品质量时,一个合格品被误判为次品的概率为0.05,一个次品被误判为合格品的概率为0.01.任意抽查一个产品,检查后被判为合格品的概率为( )
A.0.855 B.0.856 C.0.86 D.0.865
4.(2024春 太原期末)某场乒乓球单打比赛按三局两胜的赛制进行,甲乙两人参加比赛.已知每局比赛甲获胜的概率为0.4,乙获胜的概率为0.6.现用计算机产生1~5之间的整数随机数,当出现1或2时,表示此局比赛甲获胜,当出现3,4或5时,表示此局比赛乙获胜.在一次试验中,产生了20组随机数如下:
534 123 512 114 125 334 432 332 314 152
423 443 423 344 541 453 525 151 354 345
根据以上数据,利用随机模拟试验,估计甲获得冠军的概率为( )
A.0.24 B.0.3 C.0.7 D.0.76
5.(2024 云南)某公司10名员工参加岗位技能比赛,获奖情况如下:
等级 一等奖 二等奖 三等奖
人数(单位:人) 3 6 1
现从这10名员工中任选1名员工参加经验交流活动.若每位员工被选到的概率相等,则选到获一等奖员工的概率为( )
A.0.1 B.0.3 C.0.5 D.0.6
二.多选题(共4小题)
(多选)6.(2024秋 任城区校级月考)下述关于频率与概率的说法中,错误的是( )
A.设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品
B.利用随机事件发生的频率估计随机事件的概率,即使随机试验的次数超过10000,所估计出的概率也不一定很准确.
C.随机事件发生的频率就是这个随机事件发生的概率
D.做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是
(多选)7.(2024春 太原期末)下列结论正确的是( )
A.任何事件的概率总是在(0,1)内
B.随着试验次数的增加,频率会逐渐稳定于概率
C.抛掷一枚硬币,试验100次出现正面向上的频率一定比试验50次出现正面向上的频率更接近它出现正面向上的概率
D.随机事件A,B中至少有一个发生的概率一定不小于A,B中恰有一个发生的概率
(多选)8.(2024春 曲靖期末)下列说法不正确的是( )
A.某种福利彩票的中奖概率为,那么买1000张这种彩票一定能中奖
B.随着试验次数的增加,频率一般会越来越接近概率
C.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
D.某市气象台预报“明天本市降水概率为70%”,指的是该市气象台专家中,有70%认为明天会降水,30%认为不降水
(多选)9.(2023秋 德阳期末)在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入决赛(比赛采用三局两胜制,即率先获得两局胜利者赢得比赛,随即比赛结束).假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.某同学利用计算机产生1~5之间的随机数,当出现1,2或3时,表示甲获胜,当出现4或5时,表示乙获胜,以每3个随机数为一组进行冠军模拟预测,如果产生如下20组随机数:423 123 423 344 114 453 525 332 152 342 534 443 512 541 125 432 334 151 314 354,根据频率估计概率的思想,下列说法正确的有( )
A.甲获得冠军的概率近似值为0.65
B.甲以2:0的比分获得冠军的概率近似值为0.5
C.比赛总共打满三局的概率近似值为0.55
D.乙以2:0的比分获得冠军的概率近似值为0.15
三.填空题(共3小题)
10.(2024秋 四川校级期末)一个袋子中有红、黄、蓝、绿四个小球,有放回地从中任取一个小球,将“三次抽取后,红色小球,黄色小球都取到”记为事件M,用随机模拟的方法估计事件M发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表红、黄、蓝、绿四个小球,以每三个随机数为一组,表示取小球三次的结果,经随机模拟产生了以下18组随机数:
110 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计事件M发生的概率为 .
11.(2024秋 孝感期中)一个不透明的袋中装有除颜色外均相同的8个红球,4个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的频率稳定在0.4,则袋中约有绿球 个.
12.(2024秋 汉台区月考)一个容量为100的样本,其数据的分组与各组的频数如表:
(0,10] (10,20] (20,30] (30,40] (40,50] (50,60] (60,70]
12 13 24 15 16 13 7
则样本数据落在(40,70]内的频率为 .
四.解答题(共3小题)
13.(2023 甘肃一模)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C三个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费80元,50元,30元.该厂有甲、乙两个分厂可承接加工业务,甲分厂加工成本费为40元/件,乙分厂加工成本费为35元/件.该厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C
频数 45 30 25
乙分厂产品等级的频数分布表
等级 A B C
频数 40 10 50
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,该厂家应选哪个分厂承接加工业务?
14.(2022 临汾三模)我们认为灯泡寿命的总体密度曲线是正态分布曲线f(x),其中μ为总体平均数,σ为总体标准差,某品牌灯泡的总体寿命平均数μ=2600小时.
(1)随机取三个该品牌灯泡,求三个灯泡中恰有两个寿命超过2600小时的概率;
(2)该品牌灯泡寿命超过2800小时的概率为.我们通过设计模拟试验的方法解决“随机取三个该品牌灯泡,求三个灯泡中恰有两个寿命超过2800小时的概率”问题.利用计算器可以产生0到9十个随机数,我们用1,2,3,4表示寿命超过2800小时,用5,6,7,8,9,0表示寿命没有超过2800小时.因为是三个灯泡,所以每三个随机数一组.例如,产生20组随机数
就相当于做了20次试验.估计三个灯泡中恰有两个寿命超过2800小时的概率.
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
15.(2021 临汾模拟)在区间[0,1]上产生两组均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),统计yi≤xi}的点(xi,yi)数目为X.
(1)当N=1时,求X=1的概率;
(2)设平面区域Ω:.
(ⅰ)求Ω的面积S;
(ⅱ)某计算机兴趣小组用以上方法估计Ω的面积,当N=100时,求其估计值与实际值之差在区间(﹣0.1,0.1)内的概率.
附表:P(k)P(X=t).
k 39 40 41 59 60 61
P(k) 0.01760 0.02844 0.04431 0.97155 0.98239 0.98951
期末热点.重难点 频率与概率
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 湖北期末)某学校乒乓球比赛,学生甲和学生乙比赛3局(采取三局两胜制),假设每局比赛甲获胜的概率是0.7,乙获胜的概率是0.3,利用计算机模拟试验,计算机产生0 9之间的随机数,当出现随机数0 6时,表示一局甲获胜,其概率是0.7.由于要比赛3局,所以每3个随机数为一组.例如,产生20组随机数:
603 099 316 696 851 916 062 107 493 977
329 906 355 860 375 107 347 467 822 166
根据随机数估计甲获胜的概率为( )
A.0.9 B.0.95 C.0.8 D.0.85
【考点】模拟方法估计概率;随机数法简单随机抽样及其步骤.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】A
【分析】根据题意,结合随机数的含义,分析20组随机数中,表示甲获胜的组数,由古典概型公式计算可得答案
【解答】解.根据题意,20组随机数中,除099,977外,表示甲获胜的共有18组,
则据此估计甲获胜的概率为.
故选:A.
【点评】本题考查随机数的应用,考查概率的计算,属于基础题.
2.(2024秋 徐汇区校级期末)一个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.经过重复摸球足够多次试验后发现,摸到黑球的频率稳定在0.1左右,则据此估计盒子中红球的个数约为( )
A.40个 B.45个 C.50个 D.55个
【考点】频率及频率的稳定性.
【专题】整体思想;综合法;概率与统计;运算求解;数据分析.
【答案】B
【分析】根据频率和概率的关系求解.
【解答】解:设盒子中球的总数为n,
由题意可知,0.1,
解得n=50,
所以估计盒子中红球的个数约为50﹣5=45个.
故答案为:B.
【点评】本题主要考查了频率与概率的关系,属于基础题.
3.(2024秋 高邮市月考)已知一批产品中有90%是合格品,检验产品质量时,一个合格品被误判为次品的概率为0.05,一个次品被误判为合格品的概率为0.01.任意抽查一个产品,检查后被判为合格品的概率为( )
A.0.855 B.0.856 C.0.86 D.0.865
【考点】频率与概率.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】B
【分析】记事件A:抽取的一个产品为合格品,事件B:抽查一个产品被判为合格品,利用全概率公式可求得P(B)的值.
【解答】解:记事件A:抽取的一个产品为合格品,事件B:抽查一个产品被判为合格品,
一个合格品被误判为次品的概率为0.05,一个次品被误判为合格品的概率为0.01,
则P(A)=0.9,P(B|A)=0.95,,
故.
所以任意抽查一个产品,检查后被判为合格品的概率为0.856.
故选:B.
【点评】本题主要考查全概率公式,属于基础题.
4.(2024春 太原期末)某场乒乓球单打比赛按三局两胜的赛制进行,甲乙两人参加比赛.已知每局比赛甲获胜的概率为0.4,乙获胜的概率为0.6.现用计算机产生1~5之间的整数随机数,当出现1或2时,表示此局比赛甲获胜,当出现3,4或5时,表示此局比赛乙获胜.在一次试验中,产生了20组随机数如下:
534 123 512 114 125 334 432 332 314 152
423 443 423 344 541 453 525 151 354 345
根据以上数据,利用随机模拟试验,估计甲获得冠军的概率为( )
A.0.24 B.0.3 C.0.7 D.0.76
【考点】模拟方法估计概率;求随机数法抽样的样本.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据题意,在20组随机数中,表示甲获胜的有:123,512,114,125,152,151,共6种情况,然后利用古典概型的概率公式求解即可.
【解答】解:根据题意,在20组随机数中,表示甲获胜的有:123,512,114,125,152,151,共6种情况,
所以可估计甲获得冠军的概率为.
故选:B.
【点评】本题主要考查了利用随机数法模拟事件发生的概率,属于基础题.
5.(2024 云南)某公司10名员工参加岗位技能比赛,获奖情况如下:
等级 一等奖 二等奖 三等奖
人数(单位:人) 3 6 1
现从这10名员工中任选1名员工参加经验交流活动.若每位员工被选到的概率相等,则选到获一等奖员工的概率为( )
A.0.1 B.0.3 C.0.5 D.0.6
【考点】频率与概率;古典概型.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据古典概率的知识求得正确答案.
【解答】解:获一等奖员工有3个人,
根据古典概型公式可知,所求概率为.
故选:B.
【点评】本题考查古典概型,属于基础题.
二.多选题(共4小题)
(多选)6.(2024秋 任城区校级月考)下述关于频率与概率的说法中,错误的是( )
A.设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品
B.利用随机事件发生的频率估计随机事件的概率,即使随机试验的次数超过10000,所估计出的概率也不一定很准确.
C.随机事件发生的频率就是这个随机事件发生的概率
D.做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是
【考点】频率与概率.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】ACD
【分析】根据频率与概率的关系,结合各选项的描述判断正误.
【解答】解:从中任取100件,可能有10件,也可能少于10件或多于10件,A错误;
10000次的界定没有科学依据,“不一定很准确“的表达正确,试验次数越多,频率越稳定在概率值附近,
但并非试验次数越多,频率就等于概率,B正确.
多次重复试验中事件发生的频率在某一常数附近,此常数为概率,C中描述不符合概率定义,C错误;
做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的频率是,不是概率为,D错误.
故选:ACD.
【点评】本题主要考查概率与频率的定义,属于基础题.
(多选)7.(2024春 太原期末)下列结论正确的是( )
A.任何事件的概率总是在(0,1)内
B.随着试验次数的增加,频率会逐渐稳定于概率
C.抛掷一枚硬币,试验100次出现正面向上的频率一定比试验50次出现正面向上的频率更接近它出现正面向上的概率
D.随机事件A,B中至少有一个发生的概率一定不小于A,B中恰有一个发生的概率
【考点】频率与概率.
【专题】对应思想;综合法;概率与统计;逻辑思维.
【答案】BD
【分析】对于A:根据概率的性质分析判断;对于BC:根据概率和频率之间的关系分析判断;对于D:根据事件的运算结合概率的性质分析判断.
【解答】解:对于A:任何事件的概率总是在[0,1]之间,其中不可能事件的概率为0,必然事件的概率为1,故A错误;
对于B:根据频率与概率之间的关系可知:随着试验次数的增加,频率会逐渐稳定于概率,故B正确;
对于C:由选项B可知:随着试验次数的增加,频率会逐渐稳定于概率,但该结论为总体效果,对具体情况不一定成立,故C错误;
对于D:因为P(AB)≥0,则,
且随机事件A,B中至少有一个发生的概率为P(A∪B),
A,B中恰有一个发生的的概率为,
所以随机事件A,B中至少有一个发生的概率一定不小于A,B中恰有一个发生的概率,故D正确.
故选:BD.
【点评】本题考查概率的定义和性质,注意理解概率的定义,属于基础题.
(多选)8.(2024春 曲靖期末)下列说法不正确的是( )
A.某种福利彩票的中奖概率为,那么买1000张这种彩票一定能中奖
B.随着试验次数的增加,频率一般会越来越接近概率
C.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
D.某市气象台预报“明天本市降水概率为70%”,指的是该市气象台专家中,有70%认为明天会降水,30%认为不降水
【考点】频率与概率.
【专题】计算题;转化思想;综合法;概率与统计;运算求解.
【答案】ACD
【分析】根据频率和概率之间的关系、概率的定义,对各项依次判断,即可得到本题的答案.
【解答】解:对于A.中奖概率为是指买一次彩票,可能中奖的概率为,不是指1000张这种彩票一定能中奖,故A错误;
对于B,试验次数越多,频率就会稳定在概率的附近,故B正确;
对于C,某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人能治愈的可能性还是10%,故C错误;
对于D,某市气象台预报“明天本市降水概率为70%”,不是:该市气象台专家中,有70%认为明天会降水,30%认为不降水,而是明天降水概率为70%指明天该地区降水的可能性为70%,故D错误.
故选:ACD.
【点评】本题考查命题的真假的判断,概率的基本知识的应用,是基础题.
(多选)9.(2023秋 德阳期末)在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入决赛(比赛采用三局两胜制,即率先获得两局胜利者赢得比赛,随即比赛结束).假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.某同学利用计算机产生1~5之间的随机数,当出现1,2或3时,表示甲获胜,当出现4或5时,表示乙获胜,以每3个随机数为一组进行冠军模拟预测,如果产生如下20组随机数:423 123 423 344 114 453 525 332 152 342 534 443 512 541 125 432 334 151 314 354,根据频率估计概率的思想,下列说法正确的有( )
A.甲获得冠军的概率近似值为0.65
B.甲以2:0的比分获得冠军的概率近似值为0.5
C.比赛总共打满三局的概率近似值为0.55
D.乙以2:0的比分获得冠军的概率近似值为0.15
【考点】模拟方法估计概率.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】ACD
【分析】由20组随机数中分别先求出甲获得冠军的数,甲以2:0的比分获得冠军的数,比赛总共打满三局的数和乙以2:0的比分获得冠军的数,从而可求出各选项频率,进而可得答案.
【解答】解:对于A,表示甲获得冠军的数有423,123,423,114,332,152,342,512,125,432,334,151,314共13组数,
故估计该场比赛甲获胜的概率为,故A正确;
对于B,表示甲以2:0的比分获得冠军的数有:123,114,332,125,334,314,共6组数,
故估计甲以2:0的比分获得冠军概率为,故B错误;
对于C,表示比赛总共打满三局的数有:423,423,344,525,152,342,534,512,432,151,354共11组数,
故估计比赛总共打满三局的概率为,故C正确;
对于D,表示乙以2:0的比分获得冠军的数有:453,443,541共3组数,
故估计乙以2:0的比分获得冠军的概率为0.15,故D正确.
故选:ACD.
【点评】本题主要考查了简单随机抽样的应用,考查了利用频率估算概率,属于基础题.
三.填空题(共3小题)
10.(2024秋 四川校级期末)一个袋子中有红、黄、蓝、绿四个小球,有放回地从中任取一个小球,将“三次抽取后,红色小球,黄色小球都取到”记为事件M,用随机模拟的方法估计事件M发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表红、黄、蓝、绿四个小球,以每三个随机数为一组,表示取小球三次的结果,经随机模拟产生了以下18组随机数:
110 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计事件M发生的概率为 .
【考点】模拟方法估计概率.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】.
【分析】先求出事件M发生的情况,再结合古典概型的概率公式,即可求解.
【解答】解:事件M包含红色小球和黄色小球,即包含数字0和1,
随机产生的18组数中,包含0,1的有110,021,001,130,031,103,共6组,
故所求概率为.
故答案为:.
【点评】本题主要考查古典概型的概率公式,属于基础题.
11.(2024秋 孝感期中)一个不透明的袋中装有除颜色外均相同的8个红球,4个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的频率稳定在0.4,则袋中约有绿球 8 个.
【考点】频率与概率;古典概型及其概率计算公式.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】8.
【分析】用频率估计概率,根据绿球个数除以总个数即可.
【解答】解:因为通过大量重复的摸球试验后,发现摸到绿球的频率稳定在0.4,
所以利用频率估算概率,摸到绿球的概率为0.4,
设不透明的袋中有绿球x个,
则,
解得x=8.
故答案为:8.
【点评】本题主要考查了概率的概念,属于基础题.
12.(2024秋 汉台区月考)一个容量为100的样本,其数据的分组与各组的频数如表:
(0,10] (10,20] (20,30] (30,40] (40,50] (50,60] (60,70]
12 13 24 15 16 13 7
则样本数据落在(40,70]内的频率为 0.36 .
【考点】频率与概率.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】0.36.
【分析】根据已知条件,结合频率与频数的关系,即可求解.
【解答】解:由频数表可知,样本数据落在(40,70]内的频率为:.
故答案为:0.36.
【点评】本题主要考查频率与频数的关系,属于基础题.
四.解答题(共3小题)
13.(2023 甘肃一模)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C三个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费80元,50元,30元.该厂有甲、乙两个分厂可承接加工业务,甲分厂加工成本费为40元/件,乙分厂加工成本费为35元/件.该厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C
频数 45 30 25
乙分厂产品等级的频数分布表
等级 A B C
频数 40 10 50
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,该厂家应选哪个分厂承接加工业务?
【考点】离散型随机变量的均值(数学期望).
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】(1)估计甲、乙两分厂加工出来的一件产品为A级品的概率分别为0.45,0.4;
(2)甲分厂加工出来的100件产品的平均利润为17.25,乙分厂加工出来的100件产品的平均利润为17,应该选甲分厂承接加工业务.
【分析】(1)由试加工产品等级的频数分布表能分别估计甲、乙两分厂加工出来的一件产品为A级的概率.
(2)由数据分别求出甲、乙分厂加工出来的100件产品利润,比较甲、乙两分厂加工的产品的平均利润,应该选乙分厂承接加工业务.
【解答】解:(1)由试加工产品等级的频数分布表知:
甲分厂加工出来的一件产品为A级品的概率的估计值为0.45,
乙分厂加工出来的一件产品为A级品的概率的估计值为0.4;
(2)由数据知甲分厂加工出来的100件产品利润的频数分布表为:
利润 40 10 ﹣15
频数 45 30 25
∴甲分厂加工出来的100件产品的平均利润为:
[40×45+10×30+(﹣15)×25]=17.25,
乙分厂产品等级的频数分布表
利润 45 15 ﹣5
频数 40 10 50
∴乙分厂加工出来的100件产品的平均利润为:
[45×40+15×10+(﹣5)×50]=17,
比较甲、乙两分厂加工的产品的平均利润,应该选甲分厂承接加工业务.
【点评】本题考查概率、平均利润的求法,考查古典概型等基础知识,考查运算求解能力,是基础题.
14.(2022 临汾三模)我们认为灯泡寿命的总体密度曲线是正态分布曲线f(x),其中μ为总体平均数,σ为总体标准差,某品牌灯泡的总体寿命平均数μ=2600小时.
(1)随机取三个该品牌灯泡,求三个灯泡中恰有两个寿命超过2600小时的概率;
(2)该品牌灯泡寿命超过2800小时的概率为.我们通过设计模拟试验的方法解决“随机取三个该品牌灯泡,求三个灯泡中恰有两个寿命超过2800小时的概率”问题.利用计算器可以产生0到9十个随机数,我们用1,2,3,4表示寿命超过2800小时,用5,6,7,8,9,0表示寿命没有超过2800小时.因为是三个灯泡,所以每三个随机数一组.例如,产生20组随机数
就相当于做了20次试验.估计三个灯泡中恰有两个寿命超过2800小时的概率.
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
【考点】模拟方法估计概率.
【专题】计算题;整体思想;综合法;概率与统计;运算求解.
【答案】(1).
(2).
【分析】(1)根据题意可知每个灯泡寿命超过2600小时的概率都是,再利用古典概型的概率公式求解.
(2)先求出20组随机数中满足恰有两灯泡寿命超过2800小时的个数,再利用古典概型的概率公式求解.
【解答】解:(1)由题知平均数μ=2600,所以每个灯泡寿命超过2600小时的概率都是,
这个随机试验满足古典概型条件:有限性,等可能性.
设三个灯泡寿命超过2600小时分别为A,B,C;没有超过2600小时分别为,,,
则样本空间,
三个灯泡中恰有两个寿命超过2600小时的事件,
所以.
(2)20组随机数中满足恰有两灯泡寿命超过2800小时的有191,271,932,812,393共计5组,
所以三个灯泡中恰有两个灯泡寿命超过2800小时的概率估计值.
【点评】本题主要考查了古典概型的概率公式,考查了正态分布的定义.属于基础题.
15.(2021 临汾模拟)在区间[0,1]上产生两组均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),统计yi≤xi}的点(xi,yi)数目为X.
(1)当N=1时,求X=1的概率;
(2)设平面区域Ω:.
(ⅰ)求Ω的面积S;
(ⅱ)某计算机兴趣小组用以上方法估计Ω的面积,当N=100时,求其估计值与实际值之差在区间(﹣0.1,0.1)内的概率.
附表:P(k)P(X=t).
k 39 40 41 59 60 61
P(k) 0.01760 0.02844 0.04431 0.97155 0.98239 0.98951
【考点】模拟方法估计概率.
【专题】数形结合;数形结合法;概率与统计;数据分析.
【答案】(1);(2)(i),(ii)0.94311;详解见解析.
【分析】(1)根据题意可画图求解;(2)(i)由(1)中图求解即可,(ii)由题可得到估计值与随机数之间的比值关系,再根据表格求解即可.
【解答】解:(1)当N=1时,X=1,即在0≤x≤1,0≤y≤1内随机产生了一个点,并且这个点位于直线y=x下方,
由几何概型可知P;
(2)(i)由图可知S,
(ii)设面积的估计值为S′,则,
因为面积误差在区间(﹣0.1,0.1)内,即|S﹣S′|<0.1,
得0.4<S′<0.6,所以40<X<60,
P(40<X<60)0.97155﹣0.02844=0.94311.
【点评】本题考查了几何概型及其应用,属于基础题.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 湖北期末)某学校乒乓球比赛,学生甲和学生乙比赛3局(采取三局两胜制),假设每局比赛甲获胜的概率是0.7,乙获胜的概率是0.3,利用计算机模拟试验,计算机产生0 9之间的随机数,当出现随机数0 6时,表示一局甲获胜,其概率是0.7.由于要比赛3局,所以每3个随机数为一组.例如,产生20组随机数:
603 099 316 696 851 916 062 107 493 977
329 906 355 860 375 107 347 467 822 166
根据随机数估计甲获胜的概率为( )
A.0.9 B.0.95 C.0.8 D.0.85
2.(2024秋 徐汇区校级期末)一个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.经过重复摸球足够多次试验后发现,摸到黑球的频率稳定在0.1左右,则据此估计盒子中红球的个数约为( )
A.40个 B.45个 C.50个 D.55个
3.(2024秋 高邮市月考)已知一批产品中有90%是合格品,检验产品质量时,一个合格品被误判为次品的概率为0.05,一个次品被误判为合格品的概率为0.01.任意抽查一个产品,检查后被判为合格品的概率为( )
A.0.855 B.0.856 C.0.86 D.0.865
4.(2024春 太原期末)某场乒乓球单打比赛按三局两胜的赛制进行,甲乙两人参加比赛.已知每局比赛甲获胜的概率为0.4,乙获胜的概率为0.6.现用计算机产生1~5之间的整数随机数,当出现1或2时,表示此局比赛甲获胜,当出现3,4或5时,表示此局比赛乙获胜.在一次试验中,产生了20组随机数如下:
534 123 512 114 125 334 432 332 314 152
423 443 423 344 541 453 525 151 354 345
根据以上数据,利用随机模拟试验,估计甲获得冠军的概率为( )
A.0.24 B.0.3 C.0.7 D.0.76
5.(2024 云南)某公司10名员工参加岗位技能比赛,获奖情况如下:
等级 一等奖 二等奖 三等奖
人数(单位:人) 3 6 1
现从这10名员工中任选1名员工参加经验交流活动.若每位员工被选到的概率相等,则选到获一等奖员工的概率为( )
A.0.1 B.0.3 C.0.5 D.0.6
二.多选题(共4小题)
(多选)6.(2024秋 任城区校级月考)下述关于频率与概率的说法中,错误的是( )
A.设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品
B.利用随机事件发生的频率估计随机事件的概率,即使随机试验的次数超过10000,所估计出的概率也不一定很准确.
C.随机事件发生的频率就是这个随机事件发生的概率
D.做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是
(多选)7.(2024春 太原期末)下列结论正确的是( )
A.任何事件的概率总是在(0,1)内
B.随着试验次数的增加,频率会逐渐稳定于概率
C.抛掷一枚硬币,试验100次出现正面向上的频率一定比试验50次出现正面向上的频率更接近它出现正面向上的概率
D.随机事件A,B中至少有一个发生的概率一定不小于A,B中恰有一个发生的概率
(多选)8.(2024春 曲靖期末)下列说法不正确的是( )
A.某种福利彩票的中奖概率为,那么买1000张这种彩票一定能中奖
B.随着试验次数的增加,频率一般会越来越接近概率
C.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
D.某市气象台预报“明天本市降水概率为70%”,指的是该市气象台专家中,有70%认为明天会降水,30%认为不降水
(多选)9.(2023秋 德阳期末)在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入决赛(比赛采用三局两胜制,即率先获得两局胜利者赢得比赛,随即比赛结束).假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.某同学利用计算机产生1~5之间的随机数,当出现1,2或3时,表示甲获胜,当出现4或5时,表示乙获胜,以每3个随机数为一组进行冠军模拟预测,如果产生如下20组随机数:423 123 423 344 114 453 525 332 152 342 534 443 512 541 125 432 334 151 314 354,根据频率估计概率的思想,下列说法正确的有( )
A.甲获得冠军的概率近似值为0.65
B.甲以2:0的比分获得冠军的概率近似值为0.5
C.比赛总共打满三局的概率近似值为0.55
D.乙以2:0的比分获得冠军的概率近似值为0.15
三.填空题(共3小题)
10.(2024秋 四川校级期末)一个袋子中有红、黄、蓝、绿四个小球,有放回地从中任取一个小球,将“三次抽取后,红色小球,黄色小球都取到”记为事件M,用随机模拟的方法估计事件M发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表红、黄、蓝、绿四个小球,以每三个随机数为一组,表示取小球三次的结果,经随机模拟产生了以下18组随机数:
110 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计事件M发生的概率为 .
11.(2024秋 孝感期中)一个不透明的袋中装有除颜色外均相同的8个红球,4个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的频率稳定在0.4,则袋中约有绿球 个.
12.(2024秋 汉台区月考)一个容量为100的样本,其数据的分组与各组的频数如表:
(0,10] (10,20] (20,30] (30,40] (40,50] (50,60] (60,70]
12 13 24 15 16 13 7
则样本数据落在(40,70]内的频率为 .
四.解答题(共3小题)
13.(2023 甘肃一模)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C三个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费80元,50元,30元.该厂有甲、乙两个分厂可承接加工业务,甲分厂加工成本费为40元/件,乙分厂加工成本费为35元/件.该厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C
频数 45 30 25
乙分厂产品等级的频数分布表
等级 A B C
频数 40 10 50
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,该厂家应选哪个分厂承接加工业务?
14.(2022 临汾三模)我们认为灯泡寿命的总体密度曲线是正态分布曲线f(x),其中μ为总体平均数,σ为总体标准差,某品牌灯泡的总体寿命平均数μ=2600小时.
(1)随机取三个该品牌灯泡,求三个灯泡中恰有两个寿命超过2600小时的概率;
(2)该品牌灯泡寿命超过2800小时的概率为.我们通过设计模拟试验的方法解决“随机取三个该品牌灯泡,求三个灯泡中恰有两个寿命超过2800小时的概率”问题.利用计算器可以产生0到9十个随机数,我们用1,2,3,4表示寿命超过2800小时,用5,6,7,8,9,0表示寿命没有超过2800小时.因为是三个灯泡,所以每三个随机数一组.例如,产生20组随机数
就相当于做了20次试验.估计三个灯泡中恰有两个寿命超过2800小时的概率.
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
15.(2021 临汾模拟)在区间[0,1]上产生两组均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),统计yi≤xi}的点(xi,yi)数目为X.
(1)当N=1时,求X=1的概率;
(2)设平面区域Ω:.
(ⅰ)求Ω的面积S;
(ⅱ)某计算机兴趣小组用以上方法估计Ω的面积,当N=100时,求其估计值与实际值之差在区间(﹣0.1,0.1)内的概率.
附表:P(k)P(X=t).
k 39 40 41 59 60 61
P(k) 0.01760 0.02844 0.04431 0.97155 0.98239 0.98951
期末热点.重难点 频率与概率
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 湖北期末)某学校乒乓球比赛,学生甲和学生乙比赛3局(采取三局两胜制),假设每局比赛甲获胜的概率是0.7,乙获胜的概率是0.3,利用计算机模拟试验,计算机产生0 9之间的随机数,当出现随机数0 6时,表示一局甲获胜,其概率是0.7.由于要比赛3局,所以每3个随机数为一组.例如,产生20组随机数:
603 099 316 696 851 916 062 107 493 977
329 906 355 860 375 107 347 467 822 166
根据随机数估计甲获胜的概率为( )
A.0.9 B.0.95 C.0.8 D.0.85
【考点】模拟方法估计概率;随机数法简单随机抽样及其步骤.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】A
【分析】根据题意,结合随机数的含义,分析20组随机数中,表示甲获胜的组数,由古典概型公式计算可得答案
【解答】解.根据题意,20组随机数中,除099,977外,表示甲获胜的共有18组,
则据此估计甲获胜的概率为.
故选:A.
【点评】本题考查随机数的应用,考查概率的计算,属于基础题.
2.(2024秋 徐汇区校级期末)一个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.经过重复摸球足够多次试验后发现,摸到黑球的频率稳定在0.1左右,则据此估计盒子中红球的个数约为( )
A.40个 B.45个 C.50个 D.55个
【考点】频率及频率的稳定性.
【专题】整体思想;综合法;概率与统计;运算求解;数据分析.
【答案】B
【分析】根据频率和概率的关系求解.
【解答】解:设盒子中球的总数为n,
由题意可知,0.1,
解得n=50,
所以估计盒子中红球的个数约为50﹣5=45个.
故答案为:B.
【点评】本题主要考查了频率与概率的关系,属于基础题.
3.(2024秋 高邮市月考)已知一批产品中有90%是合格品,检验产品质量时,一个合格品被误判为次品的概率为0.05,一个次品被误判为合格品的概率为0.01.任意抽查一个产品,检查后被判为合格品的概率为( )
A.0.855 B.0.856 C.0.86 D.0.865
【考点】频率与概率.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】B
【分析】记事件A:抽取的一个产品为合格品,事件B:抽查一个产品被判为合格品,利用全概率公式可求得P(B)的值.
【解答】解:记事件A:抽取的一个产品为合格品,事件B:抽查一个产品被判为合格品,
一个合格品被误判为次品的概率为0.05,一个次品被误判为合格品的概率为0.01,
则P(A)=0.9,P(B|A)=0.95,,
故.
所以任意抽查一个产品,检查后被判为合格品的概率为0.856.
故选:B.
【点评】本题主要考查全概率公式,属于基础题.
4.(2024春 太原期末)某场乒乓球单打比赛按三局两胜的赛制进行,甲乙两人参加比赛.已知每局比赛甲获胜的概率为0.4,乙获胜的概率为0.6.现用计算机产生1~5之间的整数随机数,当出现1或2时,表示此局比赛甲获胜,当出现3,4或5时,表示此局比赛乙获胜.在一次试验中,产生了20组随机数如下:
534 123 512 114 125 334 432 332 314 152
423 443 423 344 541 453 525 151 354 345
根据以上数据,利用随机模拟试验,估计甲获得冠军的概率为( )
A.0.24 B.0.3 C.0.7 D.0.76
【考点】模拟方法估计概率;求随机数法抽样的样本.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据题意,在20组随机数中,表示甲获胜的有:123,512,114,125,152,151,共6种情况,然后利用古典概型的概率公式求解即可.
【解答】解:根据题意,在20组随机数中,表示甲获胜的有:123,512,114,125,152,151,共6种情况,
所以可估计甲获得冠军的概率为.
故选:B.
【点评】本题主要考查了利用随机数法模拟事件发生的概率,属于基础题.
5.(2024 云南)某公司10名员工参加岗位技能比赛,获奖情况如下:
等级 一等奖 二等奖 三等奖
人数(单位:人) 3 6 1
现从这10名员工中任选1名员工参加经验交流活动.若每位员工被选到的概率相等,则选到获一等奖员工的概率为( )
A.0.1 B.0.3 C.0.5 D.0.6
【考点】频率与概率;古典概型.
【专题】转化思想;综合法;概率与统计;运算求解.
【答案】B
【分析】根据古典概率的知识求得正确答案.
【解答】解:获一等奖员工有3个人,
根据古典概型公式可知,所求概率为.
故选:B.
【点评】本题考查古典概型,属于基础题.
二.多选题(共4小题)
(多选)6.(2024秋 任城区校级月考)下述关于频率与概率的说法中,错误的是( )
A.设有一大批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品
B.利用随机事件发生的频率估计随机事件的概率,即使随机试验的次数超过10000,所估计出的概率也不一定很准确.
C.随机事件发生的频率就是这个随机事件发生的概率
D.做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的概率是
【考点】频率与概率.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】ACD
【分析】根据频率与概率的关系,结合各选项的描述判断正误.
【解答】解:从中任取100件,可能有10件,也可能少于10件或多于10件,A错误;
10000次的界定没有科学依据,“不一定很准确“的表达正确,试验次数越多,频率越稳定在概率值附近,
但并非试验次数越多,频率就等于概率,B正确.
多次重复试验中事件发生的频率在某一常数附近,此常数为概率,C中描述不符合概率定义,C错误;
做7次抛硬币的试验,结果3次出现正面,因此,抛一枚硬币出现正面的频率是,不是概率为,D错误.
故选:ACD.
【点评】本题主要考查概率与频率的定义,属于基础题.
(多选)7.(2024春 太原期末)下列结论正确的是( )
A.任何事件的概率总是在(0,1)内
B.随着试验次数的增加,频率会逐渐稳定于概率
C.抛掷一枚硬币,试验100次出现正面向上的频率一定比试验50次出现正面向上的频率更接近它出现正面向上的概率
D.随机事件A,B中至少有一个发生的概率一定不小于A,B中恰有一个发生的概率
【考点】频率与概率.
【专题】对应思想;综合法;概率与统计;逻辑思维.
【答案】BD
【分析】对于A:根据概率的性质分析判断;对于BC:根据概率和频率之间的关系分析判断;对于D:根据事件的运算结合概率的性质分析判断.
【解答】解:对于A:任何事件的概率总是在[0,1]之间,其中不可能事件的概率为0,必然事件的概率为1,故A错误;
对于B:根据频率与概率之间的关系可知:随着试验次数的增加,频率会逐渐稳定于概率,故B正确;
对于C:由选项B可知:随着试验次数的增加,频率会逐渐稳定于概率,但该结论为总体效果,对具体情况不一定成立,故C错误;
对于D:因为P(AB)≥0,则,
且随机事件A,B中至少有一个发生的概率为P(A∪B),
A,B中恰有一个发生的的概率为,
所以随机事件A,B中至少有一个发生的概率一定不小于A,B中恰有一个发生的概率,故D正确.
故选:BD.
【点评】本题考查概率的定义和性质,注意理解概率的定义,属于基础题.
(多选)8.(2024春 曲靖期末)下列说法不正确的是( )
A.某种福利彩票的中奖概率为,那么买1000张这种彩票一定能中奖
B.随着试验次数的增加,频率一般会越来越接近概率
C.某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
D.某市气象台预报“明天本市降水概率为70%”,指的是该市气象台专家中,有70%认为明天会降水,30%认为不降水
【考点】频率与概率.
【专题】计算题;转化思想;综合法;概率与统计;运算求解.
【答案】ACD
【分析】根据频率和概率之间的关系、概率的定义,对各项依次判断,即可得到本题的答案.
【解答】解:对于A.中奖概率为是指买一次彩票,可能中奖的概率为,不是指1000张这种彩票一定能中奖,故A错误;
对于B,试验次数越多,频率就会稳定在概率的附近,故B正确;
对于C,某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人能治愈的可能性还是10%,故C错误;
对于D,某市气象台预报“明天本市降水概率为70%”,不是:该市气象台专家中,有70%认为明天会降水,30%认为不降水,而是明天降水概率为70%指明天该地区降水的可能性为70%,故D错误.
故选:ACD.
【点评】本题考查命题的真假的判断,概率的基本知识的应用,是基础题.
(多选)9.(2023秋 德阳期末)在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入决赛(比赛采用三局两胜制,即率先获得两局胜利者赢得比赛,随即比赛结束).假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.某同学利用计算机产生1~5之间的随机数,当出现1,2或3时,表示甲获胜,当出现4或5时,表示乙获胜,以每3个随机数为一组进行冠军模拟预测,如果产生如下20组随机数:423 123 423 344 114 453 525 332 152 342 534 443 512 541 125 432 334 151 314 354,根据频率估计概率的思想,下列说法正确的有( )
A.甲获得冠军的概率近似值为0.65
B.甲以2:0的比分获得冠军的概率近似值为0.5
C.比赛总共打满三局的概率近似值为0.55
D.乙以2:0的比分获得冠军的概率近似值为0.15
【考点】模拟方法估计概率.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】ACD
【分析】由20组随机数中分别先求出甲获得冠军的数,甲以2:0的比分获得冠军的数,比赛总共打满三局的数和乙以2:0的比分获得冠军的数,从而可求出各选项频率,进而可得答案.
【解答】解:对于A,表示甲获得冠军的数有423,123,423,114,332,152,342,512,125,432,334,151,314共13组数,
故估计该场比赛甲获胜的概率为,故A正确;
对于B,表示甲以2:0的比分获得冠军的数有:123,114,332,125,334,314,共6组数,
故估计甲以2:0的比分获得冠军概率为,故B错误;
对于C,表示比赛总共打满三局的数有:423,423,344,525,152,342,534,512,432,151,354共11组数,
故估计比赛总共打满三局的概率为,故C正确;
对于D,表示乙以2:0的比分获得冠军的数有:453,443,541共3组数,
故估计乙以2:0的比分获得冠军的概率为0.15,故D正确.
故选:ACD.
【点评】本题主要考查了简单随机抽样的应用,考查了利用频率估算概率,属于基础题.
三.填空题(共3小题)
10.(2024秋 四川校级期末)一个袋子中有红、黄、蓝、绿四个小球,有放回地从中任取一个小球,将“三次抽取后,红色小球,黄色小球都取到”记为事件M,用随机模拟的方法估计事件M发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表红、黄、蓝、绿四个小球,以每三个随机数为一组,表示取小球三次的结果,经随机模拟产生了以下18组随机数:
110 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计事件M发生的概率为 .
【考点】模拟方法估计概率.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】.
【分析】先求出事件M发生的情况,再结合古典概型的概率公式,即可求解.
【解答】解:事件M包含红色小球和黄色小球,即包含数字0和1,
随机产生的18组数中,包含0,1的有110,021,001,130,031,103,共6组,
故所求概率为.
故答案为:.
【点评】本题主要考查古典概型的概率公式,属于基础题.
11.(2024秋 孝感期中)一个不透明的袋中装有除颜色外均相同的8个红球,4个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的频率稳定在0.4,则袋中约有绿球 8 个.
【考点】频率与概率;古典概型及其概率计算公式.
【专题】整体思想;综合法;概率与统计;运算求解.
【答案】8.
【分析】用频率估计概率,根据绿球个数除以总个数即可.
【解答】解:因为通过大量重复的摸球试验后,发现摸到绿球的频率稳定在0.4,
所以利用频率估算概率,摸到绿球的概率为0.4,
设不透明的袋中有绿球x个,
则,
解得x=8.
故答案为:8.
【点评】本题主要考查了概率的概念,属于基础题.
12.(2024秋 汉台区月考)一个容量为100的样本,其数据的分组与各组的频数如表:
(0,10] (10,20] (20,30] (30,40] (40,50] (50,60] (60,70]
12 13 24 15 16 13 7
则样本数据落在(40,70]内的频率为 0.36 .
【考点】频率与概率.
【专题】转化思想;转化法;概率与统计;运算求解.
【答案】0.36.
【分析】根据已知条件,结合频率与频数的关系,即可求解.
【解答】解:由频数表可知,样本数据落在(40,70]内的频率为:.
故答案为:0.36.
【点评】本题主要考查频率与频数的关系,属于基础题.
四.解答题(共3小题)
13.(2023 甘肃一模)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C三个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费80元,50元,30元.该厂有甲、乙两个分厂可承接加工业务,甲分厂加工成本费为40元/件,乙分厂加工成本费为35元/件.该厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C
频数 45 30 25
乙分厂产品等级的频数分布表
等级 A B C
频数 40 10 50
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,该厂家应选哪个分厂承接加工业务?
【考点】离散型随机变量的均值(数学期望).
【专题】方程思想;定义法;概率与统计;运算求解.
【答案】(1)估计甲、乙两分厂加工出来的一件产品为A级品的概率分别为0.45,0.4;
(2)甲分厂加工出来的100件产品的平均利润为17.25,乙分厂加工出来的100件产品的平均利润为17,应该选甲分厂承接加工业务.
【分析】(1)由试加工产品等级的频数分布表能分别估计甲、乙两分厂加工出来的一件产品为A级的概率.
(2)由数据分别求出甲、乙分厂加工出来的100件产品利润,比较甲、乙两分厂加工的产品的平均利润,应该选乙分厂承接加工业务.
【解答】解:(1)由试加工产品等级的频数分布表知:
甲分厂加工出来的一件产品为A级品的概率的估计值为0.45,
乙分厂加工出来的一件产品为A级品的概率的估计值为0.4;
(2)由数据知甲分厂加工出来的100件产品利润的频数分布表为:
利润 40 10 ﹣15
频数 45 30 25
∴甲分厂加工出来的100件产品的平均利润为:
[40×45+10×30+(﹣15)×25]=17.25,
乙分厂产品等级的频数分布表
利润 45 15 ﹣5
频数 40 10 50
∴乙分厂加工出来的100件产品的平均利润为:
[45×40+15×10+(﹣5)×50]=17,
比较甲、乙两分厂加工的产品的平均利润,应该选甲分厂承接加工业务.
【点评】本题考查概率、平均利润的求法,考查古典概型等基础知识,考查运算求解能力,是基础题.
14.(2022 临汾三模)我们认为灯泡寿命的总体密度曲线是正态分布曲线f(x),其中μ为总体平均数,σ为总体标准差,某品牌灯泡的总体寿命平均数μ=2600小时.
(1)随机取三个该品牌灯泡,求三个灯泡中恰有两个寿命超过2600小时的概率;
(2)该品牌灯泡寿命超过2800小时的概率为.我们通过设计模拟试验的方法解决“随机取三个该品牌灯泡,求三个灯泡中恰有两个寿命超过2800小时的概率”问题.利用计算器可以产生0到9十个随机数,我们用1,2,3,4表示寿命超过2800小时,用5,6,7,8,9,0表示寿命没有超过2800小时.因为是三个灯泡,所以每三个随机数一组.例如,产生20组随机数
就相当于做了20次试验.估计三个灯泡中恰有两个寿命超过2800小时的概率.
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
【考点】模拟方法估计概率.
【专题】计算题;整体思想;综合法;概率与统计;运算求解.
【答案】(1).
(2).
【分析】(1)根据题意可知每个灯泡寿命超过2600小时的概率都是,再利用古典概型的概率公式求解.
(2)先求出20组随机数中满足恰有两灯泡寿命超过2800小时的个数,再利用古典概型的概率公式求解.
【解答】解:(1)由题知平均数μ=2600,所以每个灯泡寿命超过2600小时的概率都是,
这个随机试验满足古典概型条件:有限性,等可能性.
设三个灯泡寿命超过2600小时分别为A,B,C;没有超过2600小时分别为,,,
则样本空间,
三个灯泡中恰有两个寿命超过2600小时的事件,
所以.
(2)20组随机数中满足恰有两灯泡寿命超过2800小时的有191,271,932,812,393共计5组,
所以三个灯泡中恰有两个灯泡寿命超过2800小时的概率估计值.
【点评】本题主要考查了古典概型的概率公式,考查了正态分布的定义.属于基础题.
15.(2021 临汾模拟)在区间[0,1]上产生两组均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),统计yi≤xi}的点(xi,yi)数目为X.
(1)当N=1时,求X=1的概率;
(2)设平面区域Ω:.
(ⅰ)求Ω的面积S;
(ⅱ)某计算机兴趣小组用以上方法估计Ω的面积,当N=100时,求其估计值与实际值之差在区间(﹣0.1,0.1)内的概率.
附表:P(k)P(X=t).
k 39 40 41 59 60 61
P(k) 0.01760 0.02844 0.04431 0.97155 0.98239 0.98951
【考点】模拟方法估计概率.
【专题】数形结合;数形结合法;概率与统计;数据分析.
【答案】(1);(2)(i),(ii)0.94311;详解见解析.
【分析】(1)根据题意可画图求解;(2)(i)由(1)中图求解即可,(ii)由题可得到估计值与随机数之间的比值关系,再根据表格求解即可.
【解答】解:(1)当N=1时,X=1,即在0≤x≤1,0≤y≤1内随机产生了一个点,并且这个点位于直线y=x下方,
由几何概型可知P;
(2)(i)由图可知S,
(ii)设面积的估计值为S′,则,
因为面积误差在区间(﹣0.1,0.1)内,即|S﹣S′|<0.1,
得0.4<S′<0.6,所以40<X<60,
P(40<X<60)0.97155﹣0.02844=0.94311.
【点评】本题考查了几何概型及其应用,属于基础题.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
