【期末热点.重难点】直观图(含解析)2024-2025学年北师大版(2019)必修第二册数学高一下册
文档属性
| 名称 | 【期末热点.重难点】直观图(含解析)2024-2025学年北师大版(2019)必修第二册数学高一下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 890.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 00:00:00 | ||
图片预览




文档简介
期末热点.重难点 直观图
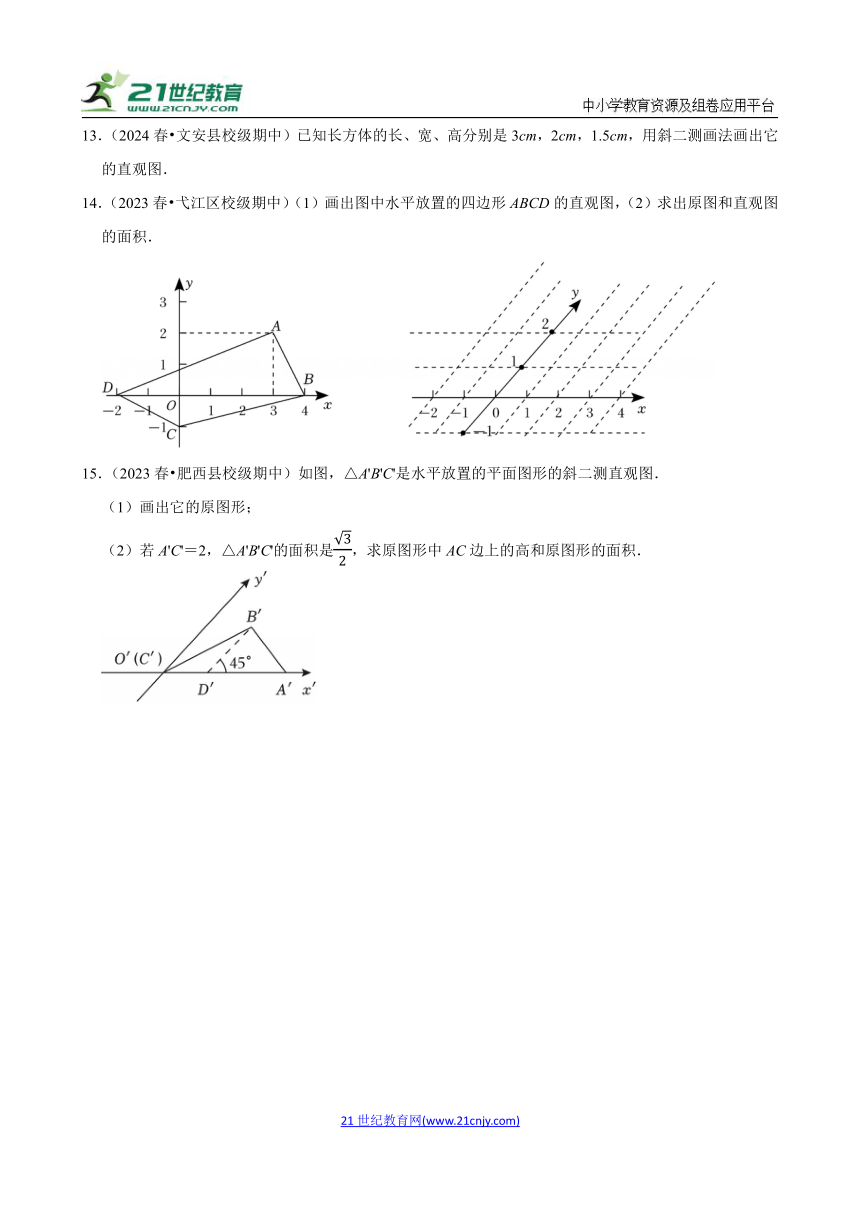
一.选择题(共5小题)
1.(2024秋 达州期末)如图所示,梯形A'B'C'D'是平面图形ABCD用斜二测画法得到的直观图,A'D'=2B'C'=2,A'B'=1,则平面图形ABCD的面积为( )
A. B.2 C.3 D.
2.(2024春 越秀区校级期末)一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
A. B.2 C. D.
3.(2023秋 柯桥区期末)已知水平放置的四边形ABCD的斜二测直观图为矩形A'B'C'D',已知A'B'=6,B'C'=3,则四边形ABCD的面积为( )
A. B. C. D.
4.(2024春 东坡区期中)一个水平放置的平面四边形ABCD,用斜二测画法画出的直观图为如图所示的矩形A′B′C′D′,已知A′B′=2,O′是A′B′的中点,则原四边形ABCD的周长为( )
A.6 B.8 C.10 D.
5.(2024秋 徐汇区校级期中)如图,用斜二测画法作△ABC的直观图得△A1B1C1,其中A1B1=B1C1,A1D1是B1C1边上的中线,由图形可知,在△ABC(D是BC的中点)中,下列结论中正确的是( )
A.AB=BC=AC B.AD⊥BC
C.AC>AD>AB>BC D.AC>AD>AB=BC
二.多选题(共4小题)
(多选)6.(2024春 济阳区校级期中)下列命题正确的是( )
A.已知,是两个不共线的向量,,,则与可以作为平面向量的一组基底
B.在△ABC中,b=11,a=20,B=30°,则这样的三角形有两个
C.已知△ABC是边长为2的正三角形,其直观图的面积为
D.已知,,若与的夹角为钝角,则k的取值范围为
(多选)7.(2024春 禄劝县校级期中)下列结论正确的是( )
A.在棱柱的所有面中,至少有两个面互相平行
B.用斜二测画法画水平放置的边长为1的正三角形,它的直观图的面积是
C.正方体ABCD﹣A1B1C1D1中,直线BD1与B1C是异面直线
D.正方体ABCD﹣A1B1C1D1中,M,N分别为BC,AB的中点,P是线段A1D1(不含端点)上的动点,过M,N,P点的平面截该正方体所得的截面为六边形
(多选)8.(2024秋 广东月考)已知水平放置的正方形的边长为,利用斜二测画法绘制该正方形在水平平面内的直观图四边形ABCD,则( )
A.∠ABD的最小值小于15°
B.∠BDC的最大值小于90°
C.|AC|的最小值大于2
D.|BD|的最大值大于4
(多选)9.(2024春 周口期末)如图所示为四边形ABCD的平面图,其中AB∥CD,AB=2CD=4,AD⊥AB,,用斜二测画法画出它的直观图四边形A'B'C'D',其中∠x'A'y'=45°,则下列说法正确的是( )
A.
B.A'B'=4
C.四边形A'B'C'D'为等腰梯形
D.四边形A'B'C'D'的周长为
三.填空题(共3小题)
10.(2024秋 上海校级期末)如图,一个水平放置的平面图形OABC的斜二测直观图是直角梯形O′A'B'C',其中O'A'∥B'C',∠O'A'B'=90°,O′A'=2B'C'=4,A'B'=2,则平面图形OABC的面积为 .
11.(2024秋 闵行区期末)如图,△A'B'C'是用斜二测画法画出的△ABC的直观图,其中OA'=OB'=OC'=1,则△ABC的面积为 .
12.(2024秋 浦东新区期末)如图,若平行四边形A′B′C′D′是用斜二测画法画出的水平放置的平面图形ABCD的直观图,已知A′B′=4cm,∠D′A′B′=45°,平行四边形A′B'C′D′的面积为8cm2,则原平面图形ABCD中AD的长度为 .
四.解答题(共3小题)
13.(2024春 文安县校级期中)已知长方体的长、宽、高分别是3cm,2cm,1.5cm,用斜二测画法画出它的直观图.
14.(2023春 弋江区校级期中)(1)画出图中水平放置的四边形ABCD的直观图,(2)求出原图和直观图的面积.
15.(2023春 肥西县校级期中)如图,△A'B'C'是水平放置的平面图形的斜二测直观图.
(1)画出它的原图形;
(2)若A'C'=2,△A'B'C'的面积是,求原图形中AC边上的高和原图形的面积.
期末热点.重难点 直观图
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 达州期末)如图所示,梯形A'B'C'D'是平面图形ABCD用斜二测画法得到的直观图,A'D'=2B'C'=2,A'B'=1,则平面图形ABCD的面积为( )
A. B.2 C.3 D.
【考点】斜二测法画直观图.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】C
【分析】根据题意,求出直观图梯形A'B'C'D'的面积,由直观图与原图的关系分析可得答案.
【解答】解:根据题意,四边形A'B'C'D'是梯形,其中A'D'=2B'C'=2,A'B'=1,
其高h=A′B′×sin45°,
则其面积S′=(A′D′+B′C′),
则平面图形ABCD的面积S=2S′=3;
故选:C.
【点评】本题考查斜二测画法,涉及平面图形的直观图,属于基础题.
2.(2024春 越秀区校级期末)一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
A. B.2 C. D.
【考点】平面图形的直观图.
【专题】计算题;空间位置关系与距离.
【答案】B
【分析】先确定直观图中的线段长,再确定平面图形中的线段长,即可求得图形的面积.
【解答】解:在直观图中,∵∠ABC=45°,AB=AD=1,DC⊥BC
∴AD=1,BC=1,
∴原来的平面图形上底长为1,下底为1,高为2,
∴平面图形的面积为2=2.
故选:B.
【点评】本题考查斜二测画法,直观图与平面图形的面积的比例关系的应用,考查计算能力.
3.(2023秋 柯桥区期末)已知水平放置的四边形ABCD的斜二测直观图为矩形A'B'C'D',已知A'B'=6,B'C'=3,则四边形ABCD的面积为( )
A. B. C. D.
【考点】斜二测法画直观图;平面图形的直观图.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】D
【分析】根据题意,求出矩形A'B'C'D'的面积,由直观图面积与原图面积的关系分析可得答案.
【解答】解:根据题意,如图:水平放置的四边形ABCD的斜二测直观图为矩形A'B'C'D',
已知A'B'=6,B'C'=3,则矩形A'B'C'D'的面积S′=6×3=18,
则四边形ABCD的面积S=2S′=36.
故选:D.
【点评】本题考查斜二测画法,涉及平面图形的直观图,属于基础题.
4.(2024春 东坡区期中)一个水平放置的平面四边形ABCD,用斜二测画法画出的直观图为如图所示的矩形A′B′C′D′,已知A′B′=2,O′是A′B′的中点,则原四边形ABCD的周长为( )
A.6 B.8 C.10 D.
【考点】由斜二测直观图还原图形.
【专题】计算题;方程思想;综合法;立体几何;运算求解.
【答案】C
【分析】根据题意,由斜二测画法作出原图矩形ABCD,分析原图中AD、BC的值,进而计算可得答案.
【解答】解:根据题意,直观图矩形A'B'C'D',A′B′=2,O′是A′B′的中点,∠C′O′B′=45°,
则A'O'=O'B'=1,B'C'=1,
则O′C′,
如图:原图矩形ABCD中,OB=1,AB=2,OC=2O′C′=2,
则AD=BC3,
原四边形ABCD的周长l=2(AB+BC)=2×(3+2)=10.
故选:C.
【点评】本题考查斜二测画法,涉及平面图形的直观图,属于基础题.
5.(2024秋 徐汇区校级期中)如图,用斜二测画法作△ABC的直观图得△A1B1C1,其中A1B1=B1C1,A1D1是B1C1边上的中线,由图形可知,在△ABC(D是BC的中点)中,下列结论中正确的是( )
A.AB=BC=AC B.AD⊥BC
C.AC>AD>AB>BC D.AC>AD>AB=BC
【考点】斜二测法画直观图;平面图形的直观图.
【专题】转化思想;数形结合法;立体几何;逻辑思维.
【答案】C
【分析】利用斜二测画法的规则结合直角三角形的性质,即可判断得到答案.
【解答】解:根据斜二测画法的规则可知,△ABC为直角三角形且AB=2BC,AB⊥BC,
则AC>AD>AB>BC.
故选:C.
【点评】本题主要考查了平面图形的直观图的画法及应用,其中熟记斜二测画法的规则是解答的关键,考查了数形结合思想的应用,属于基础题.
二.多选题(共4小题)
(多选)6.(2024春 济阳区校级期中)下列命题正确的是( )
A.已知,是两个不共线的向量,,,则与可以作为平面向量的一组基底
B.在△ABC中,b=11,a=20,B=30°,则这样的三角形有两个
C.已知△ABC是边长为2的正三角形,其直观图的面积为
D.已知,,若与的夹角为钝角,则k的取值范围为
【考点】平面图形的直观图;平面向量的基本定理;正弦定理.
【专题】整体思想;综合法;解三角形;平面向量及应用;运算求解.
【答案】ABC
【分析】利用基底的定义可判断A;利用正弦定理可判断B;利用原图形面积与直观图面积的比值可判断C;利用向量坐标的线性运算求出,再根据夹角为钝角,可得且与()不平行,求出k的范围可判断D.
【解答】解:对于A,设,是两个不共线的向量,,,
设,(k为常数),即,则,故k不存在,
则与不平行,可作为平面向量的一组基底,A正确;
对于B,在△ABC中,b=11,a=20,B=30°,
因为,可得,
因为a>b,故A>B,这样的三角形有两个,故B正确;
对于C,边长为2的正三角形的面积为,
原图面积:直观图面积,
故直观图的面积为,C正确;
对于D,,,故,
若与的夹角为钝角,
则且与()不平行,
即6k+1<0且3×2≠﹣4(2k+3),
解得且,故D错误.
故选:ABC.
【点评】本题主要考查了基底的定义,考查了利用正弦定理判断三角形个数,以及平面图形的直观图面积,向量夹角问题,属于中档题.
(多选)7.(2024春 禄劝县校级期中)下列结论正确的是( )
A.在棱柱的所有面中,至少有两个面互相平行
B.用斜二测画法画水平放置的边长为1的正三角形,它的直观图的面积是
C.正方体ABCD﹣A1B1C1D1中,直线BD1与B1C是异面直线
D.正方体ABCD﹣A1B1C1D1中,M,N分别为BC,AB的中点,P是线段A1D1(不含端点)上的动点,过M,N,P点的平面截该正方体所得的截面为六边形
【考点】斜二测法画直观图;平面的基本性质及推论;异面直线的判定;命题的真假判断与应用;棱柱的结构特征.
【专题】对应思想;数形结合法;立体几何;运算求解.
【答案】ACD
【分析】根据棱柱的性质即可判断A,根据斜二测画法的性质即可求解B,由异面直线的定义即可判断C,根据平面基本性质即可作出截面判断D.
【解答】解:对于A,由棱柱的性质可知:棱柱的上下底面互相平行,故A正确,
对于B,根据斜二测画法的规则可知:直观图中,高,
所以直观图的面积是,故B错误,
对于C,由于在正方体ABCD﹣A1B1C1D1中,直线BD1与B1C既不平行也不相交,所以是异面直线,故C正确,
对于D,延长MN,DA相交于E,连接PE交AA1于点F,同理延长MN,DC交于点H,
由于M,N是中点,所以MN∥AC,AC∥A1C1 A1C1∥MN,
故在平面A1B1C1D1中,作PQ∥A1C1交边C1D1于Q,连接QH交CC1于G,
因此六边形MNFPQG即为所求截面六边形,故D正确,
故选:ACD.
【点评】本题考查斜二测画法相关知识,属于中档题.
(多选)8.(2024秋 广东月考)已知水平放置的正方形的边长为,利用斜二测画法绘制该正方形在水平平面内的直观图四边形ABCD,则( )
A.∠ABD的最小值小于15°
B.∠BDC的最大值小于90°
C.|AC|的最小值大于2
D.|BD|的最大值大于4
【考点】斜二测法画直观图.
【专题】转化思想;数形结合法;立体几何;运算求解.
【答案】AD
【分析】根据题意,由斜二测画法的性质,画出直观图,然后对选项逐一判断,即可得到结果.
【解答】解:正方形的一条边与x′轴重合时,由斜二测画法的性质,
另一条边与y′轴重合,如图所示:
由于对称性与旋转可换性,图中∠ACB与∠BDC均等价为所求角,
由斜二测画法图形性质知,AB=CD,BC=AD=2,∠CAB+∠ACB=θ1=45°,
过A作BC的垂线,则tan∠ACB,
即∠ACB<15°,故∠ABD的最小值小于15°,选项A正确;
过D作BC的垂线,易有θ2=45°,
且,
故θ3>45°,则∠BDC>90°,∠BDC的最大值大于90°,选项B错误;
设图形绕C点逆时针旋转α,
则,
即
,
其中,则最小值为,
最大值为,选项C错误,选项D正确.
故选:AD.
【点评】本题考查了斜二测画法应用问题,是中档题.
(多选)9.(2024春 周口期末)如图所示为四边形ABCD的平面图,其中AB∥CD,AB=2CD=4,AD⊥AB,,用斜二测画法画出它的直观图四边形A'B'C'D',其中∠x'A'y'=45°,则下列说法正确的是( )
A.
B.A'B'=4
C.四边形A'B'C'D'为等腰梯形
D.四边形A'B'C'D'的周长为
【考点】由斜二测直观图还原图形.
【专题】整体思想;综合法;立体几何;运算求解.
【答案】BC
【分析】由题意可画出其直观图,再结合斜二测画法的规则求解即可.
【解答】解:由题意可画出其直观图如下,
其中A'B'∥C'D',A'B'=AB=4,C'D'=CD=2,,
故A错误,B正确;
过点D',C'分别作D'M⊥A'B',C'N⊥A'B',垂足分别为点M,N,
故A'M=D'M=C'N=A'D'sin45°=1,NB'=A'B'﹣C'D'﹣A'M=1,
故B'C',则四边形A'B'C'D'为等腰梯形,故C正确;
故四边形A'B'C'D'的周长为,即D错误.
故选:BC.
【点评】本题主要考查了平面图形的直观图,属于基础题.
三.填空题(共3小题)
10.(2024秋 上海校级期末)如图,一个水平放置的平面图形OABC的斜二测直观图是直角梯形O′A'B'C',其中O'A'∥B'C',∠O'A'B'=90°,O′A'=2B'C'=4,A'B'=2,则平面图形OABC的面积为 12 .
【考点】平面图形的直观图.
【专题】转化思想;综合法;立体几何;运算求解.
【答案】12.
【分析】根据给定条件,求出O′C′,再作出水平放置的原平面图形作答.
【解答】解:在直角梯形O′A′B′C′中,O′A′∥B′C′,O′A′=2B′C′=4,A′B′=2,
显然∠A′O′C′=45°,于是O′C′2,
直角梯形O′A′B′C′对应的原平面图形为如图中直角梯形OABC,
BC∥OA,OC⊥OA,OA=2BC=4,OC=2O′C′=4,
所以该平面图形的高为4,
故平面图形OABC的面积为:(2+4)×412.
故答案为:12.
【点评】本题考查了直观图的画法与应用问题,是基础题.
11.(2024秋 闵行区期末)如图,△A'B'C'是用斜二测画法画出的△ABC的直观图,其中OA'=OB'=OC'=1,则△ABC的面积为 2 .
【考点】斜二测法画直观图.
【专题】转化思想;综合法;坐标系和参数方程;运算求解.
【答案】2.
【分析】利用原图和直观图的对应关系将直观图还原,即可得到原三角形的面积.
【解答】解:如图,根据原图和直观图的对应关系将直观图还原,
则OB=OC=1,OA=2,
△ABC的面积为.
故答案为:2.
【点评】本题考查了直观图,属于基础题.
12.(2024秋 浦东新区期末)如图,若平行四边形A′B′C′D′是用斜二测画法画出的水平放置的平面图形ABCD的直观图,已知A′B′=4cm,∠D′A′B′=45°,平行四边形A′B'C′D′的面积为8cm2,则原平面图形ABCD中AD的长度为 4cm .
【考点】由斜二测直观图还原图形.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】4cm.
【分析】根据题意,分析可得直观图中A′D′的长度,结合斜二测画法分析可得答案.
【解答】解:根据题意,平行四边形A′B'C′D′中,A′B′=4cm,∠D′A′B′=45°,其面积为8cm2,
则有S=A′B′×A′D′×sin∠D′A′B′=8cm2,解可得A′D′=24cm,
在原图中,∠DAB=90°,AD=2A′D′=4cm;
故答案为:4cm.
【点评】本题考查斜二测画法的应用,注意斜二测画法中的长度关系,属于基础题.
四.解答题(共3小题)
13.(2024春 文安县校级期中)已知长方体的长、宽、高分别是3cm,2cm,1.5cm,用斜二测画法画出它的直观图.
【考点】空间几何体的直观图;斜二测法画直观图.
【专题】对应思想;综合法;空间位置关系与距离;直观想象.
【答案】见解答.
【分析】画棱柱的直观图,通常将其底面水平放置,利用斜二测画法画出底面,再画出侧棱,就可以得到棱柱的直观图,长方体是一种特殊的棱柱,为画图简便,可取经过长方体的三条棱所在直线为x轴,y轴,z轴.
【解答】解:(1)画轴,如图,画x轴,y轴,z轴,三轴相交于点O(A),使∠xOy=45°,∠xOz=90°.
(2)画底面,在x轴正半轴上取线段AB,使AB=3cm,在y轴正半轴上取线段AD,使AD=1cm,
过点B作y轴的平行线,过点D作x轴的平行线,设它们的交点为C,
则长方形ABCD就是长方体的底面ABCD的直观图.
(3)画侧棱,在z轴正半轴上取线段AA′,使AA′=1.5cm,
过B,C,D各点分别作z轴的平行线,在这些平行线上分别截取1.5cm长的线段BB′,CC′,DD′.
(4)成图,顺次连接A′,B′,C′,D′,工加以整理(去掉辅助线,将被遮挡的部分改为虚线),
就得到长方体的直观图.
【点评】本题考查空间几何体的直观图的画法,考查斜二测画法的规则,是中档题.
14.(2023春 弋江区校级期中)(1)画出图中水平放置的四边形ABCD的直观图,(2)求出原图和直观图的面积.
【考点】平面图形的直观图;斜二测法画直观图.
【专题】转化思想;综合法;空间位置关系与距离;逻辑思维;运算求解.
【答案】(1)见解答过程;(2)9;.
【分析】(1)确定各点对应点的位置,即可求出直观图;
(2)根据面积公式计算能求出结果.
【解答】解:(1)由斜二测法:纵向减半,横向不变,
即可知A,C的对应点为A′(3,1),C′(0,),
而B,D对应点位置不变,即B′(4,0),D′(﹣2,0),
则四边形ABCD的直观图如图:
(2)原图的面积SABCD=S△ABD+S△ABD9,
直观图的面积SA'B'C'D'=S△A'B'D'+S△B'C'D'.
【点评】本题考查斜二测法、直观图作法、原图和直观图的面积等基础知识,考查运算求解能力,是基础题.
15.(2023春 肥西县校级期中)如图,△A'B'C'是水平放置的平面图形的斜二测直观图.
(1)画出它的原图形;
(2)若A'C'=2,△A'B'C'的面积是,求原图形中AC边上的高和原图形的面积.
【考点】由斜二测直观图还原图形.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】(1)原图见解析;(2)原图形中AC边上的高为,其面积为.
【分析】(1)根据题意,由斜二测画法分析可得原图,
(2)根据题意,由三角形面积公式求出B'D'的长,结合斜二测画法可得原图中BD的长,计算其面积可得答案.
【解答】解:(1)根据题意,直观图B′D′∥y′轴,则原图中,BD∥y轴,即BD与x轴垂直,
其原图如图:
(2)由(1)的结论,BD与x轴垂直,原图中,AC边上的高为BD,
若A'C'=2,△A'B'C'的面积是,则有A'C'×B'D'×sin45°,解可得B'D',
故原图形中AC边上的高BD,
原图的面积SAC×BD.
【点评】本题考查平面图形的直观图,涉及斜二测画法,属于基础题.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 达州期末)如图所示,梯形A'B'C'D'是平面图形ABCD用斜二测画法得到的直观图,A'D'=2B'C'=2,A'B'=1,则平面图形ABCD的面积为( )
A. B.2 C.3 D.
2.(2024春 越秀区校级期末)一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
A. B.2 C. D.
3.(2023秋 柯桥区期末)已知水平放置的四边形ABCD的斜二测直观图为矩形A'B'C'D',已知A'B'=6,B'C'=3,则四边形ABCD的面积为( )
A. B. C. D.
4.(2024春 东坡区期中)一个水平放置的平面四边形ABCD,用斜二测画法画出的直观图为如图所示的矩形A′B′C′D′,已知A′B′=2,O′是A′B′的中点,则原四边形ABCD的周长为( )
A.6 B.8 C.10 D.
5.(2024秋 徐汇区校级期中)如图,用斜二测画法作△ABC的直观图得△A1B1C1,其中A1B1=B1C1,A1D1是B1C1边上的中线,由图形可知,在△ABC(D是BC的中点)中,下列结论中正确的是( )
A.AB=BC=AC B.AD⊥BC
C.AC>AD>AB>BC D.AC>AD>AB=BC
二.多选题(共4小题)
(多选)6.(2024春 济阳区校级期中)下列命题正确的是( )
A.已知,是两个不共线的向量,,,则与可以作为平面向量的一组基底
B.在△ABC中,b=11,a=20,B=30°,则这样的三角形有两个
C.已知△ABC是边长为2的正三角形,其直观图的面积为
D.已知,,若与的夹角为钝角,则k的取值范围为
(多选)7.(2024春 禄劝县校级期中)下列结论正确的是( )
A.在棱柱的所有面中,至少有两个面互相平行
B.用斜二测画法画水平放置的边长为1的正三角形,它的直观图的面积是
C.正方体ABCD﹣A1B1C1D1中,直线BD1与B1C是异面直线
D.正方体ABCD﹣A1B1C1D1中,M,N分别为BC,AB的中点,P是线段A1D1(不含端点)上的动点,过M,N,P点的平面截该正方体所得的截面为六边形
(多选)8.(2024秋 广东月考)已知水平放置的正方形的边长为,利用斜二测画法绘制该正方形在水平平面内的直观图四边形ABCD,则( )
A.∠ABD的最小值小于15°
B.∠BDC的最大值小于90°
C.|AC|的最小值大于2
D.|BD|的最大值大于4
(多选)9.(2024春 周口期末)如图所示为四边形ABCD的平面图,其中AB∥CD,AB=2CD=4,AD⊥AB,,用斜二测画法画出它的直观图四边形A'B'C'D',其中∠x'A'y'=45°,则下列说法正确的是( )
A.
B.A'B'=4
C.四边形A'B'C'D'为等腰梯形
D.四边形A'B'C'D'的周长为
三.填空题(共3小题)
10.(2024秋 上海校级期末)如图,一个水平放置的平面图形OABC的斜二测直观图是直角梯形O′A'B'C',其中O'A'∥B'C',∠O'A'B'=90°,O′A'=2B'C'=4,A'B'=2,则平面图形OABC的面积为 .
11.(2024秋 闵行区期末)如图,△A'B'C'是用斜二测画法画出的△ABC的直观图,其中OA'=OB'=OC'=1,则△ABC的面积为 .
12.(2024秋 浦东新区期末)如图,若平行四边形A′B′C′D′是用斜二测画法画出的水平放置的平面图形ABCD的直观图,已知A′B′=4cm,∠D′A′B′=45°,平行四边形A′B'C′D′的面积为8cm2,则原平面图形ABCD中AD的长度为 .
四.解答题(共3小题)
13.(2024春 文安县校级期中)已知长方体的长、宽、高分别是3cm,2cm,1.5cm,用斜二测画法画出它的直观图.
14.(2023春 弋江区校级期中)(1)画出图中水平放置的四边形ABCD的直观图,(2)求出原图和直观图的面积.
15.(2023春 肥西县校级期中)如图,△A'B'C'是水平放置的平面图形的斜二测直观图.
(1)画出它的原图形;
(2)若A'C'=2,△A'B'C'的面积是,求原图形中AC边上的高和原图形的面积.
期末热点.重难点 直观图
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 达州期末)如图所示,梯形A'B'C'D'是平面图形ABCD用斜二测画法得到的直观图,A'D'=2B'C'=2,A'B'=1,则平面图形ABCD的面积为( )
A. B.2 C.3 D.
【考点】斜二测法画直观图.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】C
【分析】根据题意,求出直观图梯形A'B'C'D'的面积,由直观图与原图的关系分析可得答案.
【解答】解:根据题意,四边形A'B'C'D'是梯形,其中A'D'=2B'C'=2,A'B'=1,
其高h=A′B′×sin45°,
则其面积S′=(A′D′+B′C′),
则平面图形ABCD的面积S=2S′=3;
故选:C.
【点评】本题考查斜二测画法,涉及平面图形的直观图,属于基础题.
2.(2024春 越秀区校级期末)一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
A. B.2 C. D.
【考点】平面图形的直观图.
【专题】计算题;空间位置关系与距离.
【答案】B
【分析】先确定直观图中的线段长,再确定平面图形中的线段长,即可求得图形的面积.
【解答】解:在直观图中,∵∠ABC=45°,AB=AD=1,DC⊥BC
∴AD=1,BC=1,
∴原来的平面图形上底长为1,下底为1,高为2,
∴平面图形的面积为2=2.
故选:B.
【点评】本题考查斜二测画法,直观图与平面图形的面积的比例关系的应用,考查计算能力.
3.(2023秋 柯桥区期末)已知水平放置的四边形ABCD的斜二测直观图为矩形A'B'C'D',已知A'B'=6,B'C'=3,则四边形ABCD的面积为( )
A. B. C. D.
【考点】斜二测法画直观图;平面图形的直观图.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】D
【分析】根据题意,求出矩形A'B'C'D'的面积,由直观图面积与原图面积的关系分析可得答案.
【解答】解:根据题意,如图:水平放置的四边形ABCD的斜二测直观图为矩形A'B'C'D',
已知A'B'=6,B'C'=3,则矩形A'B'C'D'的面积S′=6×3=18,
则四边形ABCD的面积S=2S′=36.
故选:D.
【点评】本题考查斜二测画法,涉及平面图形的直观图,属于基础题.
4.(2024春 东坡区期中)一个水平放置的平面四边形ABCD,用斜二测画法画出的直观图为如图所示的矩形A′B′C′D′,已知A′B′=2,O′是A′B′的中点,则原四边形ABCD的周长为( )
A.6 B.8 C.10 D.
【考点】由斜二测直观图还原图形.
【专题】计算题;方程思想;综合法;立体几何;运算求解.
【答案】C
【分析】根据题意,由斜二测画法作出原图矩形ABCD,分析原图中AD、BC的值,进而计算可得答案.
【解答】解:根据题意,直观图矩形A'B'C'D',A′B′=2,O′是A′B′的中点,∠C′O′B′=45°,
则A'O'=O'B'=1,B'C'=1,
则O′C′,
如图:原图矩形ABCD中,OB=1,AB=2,OC=2O′C′=2,
则AD=BC3,
原四边形ABCD的周长l=2(AB+BC)=2×(3+2)=10.
故选:C.
【点评】本题考查斜二测画法,涉及平面图形的直观图,属于基础题.
5.(2024秋 徐汇区校级期中)如图,用斜二测画法作△ABC的直观图得△A1B1C1,其中A1B1=B1C1,A1D1是B1C1边上的中线,由图形可知,在△ABC(D是BC的中点)中,下列结论中正确的是( )
A.AB=BC=AC B.AD⊥BC
C.AC>AD>AB>BC D.AC>AD>AB=BC
【考点】斜二测法画直观图;平面图形的直观图.
【专题】转化思想;数形结合法;立体几何;逻辑思维.
【答案】C
【分析】利用斜二测画法的规则结合直角三角形的性质,即可判断得到答案.
【解答】解:根据斜二测画法的规则可知,△ABC为直角三角形且AB=2BC,AB⊥BC,
则AC>AD>AB>BC.
故选:C.
【点评】本题主要考查了平面图形的直观图的画法及应用,其中熟记斜二测画法的规则是解答的关键,考查了数形结合思想的应用,属于基础题.
二.多选题(共4小题)
(多选)6.(2024春 济阳区校级期中)下列命题正确的是( )
A.已知,是两个不共线的向量,,,则与可以作为平面向量的一组基底
B.在△ABC中,b=11,a=20,B=30°,则这样的三角形有两个
C.已知△ABC是边长为2的正三角形,其直观图的面积为
D.已知,,若与的夹角为钝角,则k的取值范围为
【考点】平面图形的直观图;平面向量的基本定理;正弦定理.
【专题】整体思想;综合法;解三角形;平面向量及应用;运算求解.
【答案】ABC
【分析】利用基底的定义可判断A;利用正弦定理可判断B;利用原图形面积与直观图面积的比值可判断C;利用向量坐标的线性运算求出,再根据夹角为钝角,可得且与()不平行,求出k的范围可判断D.
【解答】解:对于A,设,是两个不共线的向量,,,
设,(k为常数),即,则,故k不存在,
则与不平行,可作为平面向量的一组基底,A正确;
对于B,在△ABC中,b=11,a=20,B=30°,
因为,可得,
因为a>b,故A>B,这样的三角形有两个,故B正确;
对于C,边长为2的正三角形的面积为,
原图面积:直观图面积,
故直观图的面积为,C正确;
对于D,,,故,
若与的夹角为钝角,
则且与()不平行,
即6k+1<0且3×2≠﹣4(2k+3),
解得且,故D错误.
故选:ABC.
【点评】本题主要考查了基底的定义,考查了利用正弦定理判断三角形个数,以及平面图形的直观图面积,向量夹角问题,属于中档题.
(多选)7.(2024春 禄劝县校级期中)下列结论正确的是( )
A.在棱柱的所有面中,至少有两个面互相平行
B.用斜二测画法画水平放置的边长为1的正三角形,它的直观图的面积是
C.正方体ABCD﹣A1B1C1D1中,直线BD1与B1C是异面直线
D.正方体ABCD﹣A1B1C1D1中,M,N分别为BC,AB的中点,P是线段A1D1(不含端点)上的动点,过M,N,P点的平面截该正方体所得的截面为六边形
【考点】斜二测法画直观图;平面的基本性质及推论;异面直线的判定;命题的真假判断与应用;棱柱的结构特征.
【专题】对应思想;数形结合法;立体几何;运算求解.
【答案】ACD
【分析】根据棱柱的性质即可判断A,根据斜二测画法的性质即可求解B,由异面直线的定义即可判断C,根据平面基本性质即可作出截面判断D.
【解答】解:对于A,由棱柱的性质可知:棱柱的上下底面互相平行,故A正确,
对于B,根据斜二测画法的规则可知:直观图中,高,
所以直观图的面积是,故B错误,
对于C,由于在正方体ABCD﹣A1B1C1D1中,直线BD1与B1C既不平行也不相交,所以是异面直线,故C正确,
对于D,延长MN,DA相交于E,连接PE交AA1于点F,同理延长MN,DC交于点H,
由于M,N是中点,所以MN∥AC,AC∥A1C1 A1C1∥MN,
故在平面A1B1C1D1中,作PQ∥A1C1交边C1D1于Q,连接QH交CC1于G,
因此六边形MNFPQG即为所求截面六边形,故D正确,
故选:ACD.
【点评】本题考查斜二测画法相关知识,属于中档题.
(多选)8.(2024秋 广东月考)已知水平放置的正方形的边长为,利用斜二测画法绘制该正方形在水平平面内的直观图四边形ABCD,则( )
A.∠ABD的最小值小于15°
B.∠BDC的最大值小于90°
C.|AC|的最小值大于2
D.|BD|的最大值大于4
【考点】斜二测法画直观图.
【专题】转化思想;数形结合法;立体几何;运算求解.
【答案】AD
【分析】根据题意,由斜二测画法的性质,画出直观图,然后对选项逐一判断,即可得到结果.
【解答】解:正方形的一条边与x′轴重合时,由斜二测画法的性质,
另一条边与y′轴重合,如图所示:
由于对称性与旋转可换性,图中∠ACB与∠BDC均等价为所求角,
由斜二测画法图形性质知,AB=CD,BC=AD=2,∠CAB+∠ACB=θ1=45°,
过A作BC的垂线,则tan∠ACB,
即∠ACB<15°,故∠ABD的最小值小于15°,选项A正确;
过D作BC的垂线,易有θ2=45°,
且,
故θ3>45°,则∠BDC>90°,∠BDC的最大值大于90°,选项B错误;
设图形绕C点逆时针旋转α,
则,
即
,
其中,则最小值为,
最大值为,选项C错误,选项D正确.
故选:AD.
【点评】本题考查了斜二测画法应用问题,是中档题.
(多选)9.(2024春 周口期末)如图所示为四边形ABCD的平面图,其中AB∥CD,AB=2CD=4,AD⊥AB,,用斜二测画法画出它的直观图四边形A'B'C'D',其中∠x'A'y'=45°,则下列说法正确的是( )
A.
B.A'B'=4
C.四边形A'B'C'D'为等腰梯形
D.四边形A'B'C'D'的周长为
【考点】由斜二测直观图还原图形.
【专题】整体思想;综合法;立体几何;运算求解.
【答案】BC
【分析】由题意可画出其直观图,再结合斜二测画法的规则求解即可.
【解答】解:由题意可画出其直观图如下,
其中A'B'∥C'D',A'B'=AB=4,C'D'=CD=2,,
故A错误,B正确;
过点D',C'分别作D'M⊥A'B',C'N⊥A'B',垂足分别为点M,N,
故A'M=D'M=C'N=A'D'sin45°=1,NB'=A'B'﹣C'D'﹣A'M=1,
故B'C',则四边形A'B'C'D'为等腰梯形,故C正确;
故四边形A'B'C'D'的周长为,即D错误.
故选:BC.
【点评】本题主要考查了平面图形的直观图,属于基础题.
三.填空题(共3小题)
10.(2024秋 上海校级期末)如图,一个水平放置的平面图形OABC的斜二测直观图是直角梯形O′A'B'C',其中O'A'∥B'C',∠O'A'B'=90°,O′A'=2B'C'=4,A'B'=2,则平面图形OABC的面积为 12 .
【考点】平面图形的直观图.
【专题】转化思想;综合法;立体几何;运算求解.
【答案】12.
【分析】根据给定条件,求出O′C′,再作出水平放置的原平面图形作答.
【解答】解:在直角梯形O′A′B′C′中,O′A′∥B′C′,O′A′=2B′C′=4,A′B′=2,
显然∠A′O′C′=45°,于是O′C′2,
直角梯形O′A′B′C′对应的原平面图形为如图中直角梯形OABC,
BC∥OA,OC⊥OA,OA=2BC=4,OC=2O′C′=4,
所以该平面图形的高为4,
故平面图形OABC的面积为:(2+4)×412.
故答案为:12.
【点评】本题考查了直观图的画法与应用问题,是基础题.
11.(2024秋 闵行区期末)如图,△A'B'C'是用斜二测画法画出的△ABC的直观图,其中OA'=OB'=OC'=1,则△ABC的面积为 2 .
【考点】斜二测法画直观图.
【专题】转化思想;综合法;坐标系和参数方程;运算求解.
【答案】2.
【分析】利用原图和直观图的对应关系将直观图还原,即可得到原三角形的面积.
【解答】解:如图,根据原图和直观图的对应关系将直观图还原,
则OB=OC=1,OA=2,
△ABC的面积为.
故答案为:2.
【点评】本题考查了直观图,属于基础题.
12.(2024秋 浦东新区期末)如图,若平行四边形A′B′C′D′是用斜二测画法画出的水平放置的平面图形ABCD的直观图,已知A′B′=4cm,∠D′A′B′=45°,平行四边形A′B'C′D′的面积为8cm2,则原平面图形ABCD中AD的长度为 4cm .
【考点】由斜二测直观图还原图形.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】4cm.
【分析】根据题意,分析可得直观图中A′D′的长度,结合斜二测画法分析可得答案.
【解答】解:根据题意,平行四边形A′B'C′D′中,A′B′=4cm,∠D′A′B′=45°,其面积为8cm2,
则有S=A′B′×A′D′×sin∠D′A′B′=8cm2,解可得A′D′=24cm,
在原图中,∠DAB=90°,AD=2A′D′=4cm;
故答案为:4cm.
【点评】本题考查斜二测画法的应用,注意斜二测画法中的长度关系,属于基础题.
四.解答题(共3小题)
13.(2024春 文安县校级期中)已知长方体的长、宽、高分别是3cm,2cm,1.5cm,用斜二测画法画出它的直观图.
【考点】空间几何体的直观图;斜二测法画直观图.
【专题】对应思想;综合法;空间位置关系与距离;直观想象.
【答案】见解答.
【分析】画棱柱的直观图,通常将其底面水平放置,利用斜二测画法画出底面,再画出侧棱,就可以得到棱柱的直观图,长方体是一种特殊的棱柱,为画图简便,可取经过长方体的三条棱所在直线为x轴,y轴,z轴.
【解答】解:(1)画轴,如图,画x轴,y轴,z轴,三轴相交于点O(A),使∠xOy=45°,∠xOz=90°.
(2)画底面,在x轴正半轴上取线段AB,使AB=3cm,在y轴正半轴上取线段AD,使AD=1cm,
过点B作y轴的平行线,过点D作x轴的平行线,设它们的交点为C,
则长方形ABCD就是长方体的底面ABCD的直观图.
(3)画侧棱,在z轴正半轴上取线段AA′,使AA′=1.5cm,
过B,C,D各点分别作z轴的平行线,在这些平行线上分别截取1.5cm长的线段BB′,CC′,DD′.
(4)成图,顺次连接A′,B′,C′,D′,工加以整理(去掉辅助线,将被遮挡的部分改为虚线),
就得到长方体的直观图.
【点评】本题考查空间几何体的直观图的画法,考查斜二测画法的规则,是中档题.
14.(2023春 弋江区校级期中)(1)画出图中水平放置的四边形ABCD的直观图,(2)求出原图和直观图的面积.
【考点】平面图形的直观图;斜二测法画直观图.
【专题】转化思想;综合法;空间位置关系与距离;逻辑思维;运算求解.
【答案】(1)见解答过程;(2)9;.
【分析】(1)确定各点对应点的位置,即可求出直观图;
(2)根据面积公式计算能求出结果.
【解答】解:(1)由斜二测法:纵向减半,横向不变,
即可知A,C的对应点为A′(3,1),C′(0,),
而B,D对应点位置不变,即B′(4,0),D′(﹣2,0),
则四边形ABCD的直观图如图:
(2)原图的面积SABCD=S△ABD+S△ABD9,
直观图的面积SA'B'C'D'=S△A'B'D'+S△B'C'D'.
【点评】本题考查斜二测法、直观图作法、原图和直观图的面积等基础知识,考查运算求解能力,是基础题.
15.(2023春 肥西县校级期中)如图,△A'B'C'是水平放置的平面图形的斜二测直观图.
(1)画出它的原图形;
(2)若A'C'=2,△A'B'C'的面积是,求原图形中AC边上的高和原图形的面积.
【考点】由斜二测直观图还原图形.
【专题】计算题;方程思想;转化思想;综合法;立体几何;运算求解.
【答案】(1)原图见解析;(2)原图形中AC边上的高为,其面积为.
【分析】(1)根据题意,由斜二测画法分析可得原图,
(2)根据题意,由三角形面积公式求出B'D'的长,结合斜二测画法可得原图中BD的长,计算其面积可得答案.
【解答】解:(1)根据题意,直观图B′D′∥y′轴,则原图中,BD∥y轴,即BD与x轴垂直,
其原图如图:
(2)由(1)的结论,BD与x轴垂直,原图中,AC边上的高为BD,
若A'C'=2,△A'B'C'的面积是,则有A'C'×B'D'×sin45°,解可得B'D',
故原图形中AC边上的高BD,
原图的面积SAC×BD.
【点评】本题考查平面图形的直观图,涉及斜二测画法,属于基础题.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
