【期末热点.重难点】任意角(含解析)2024-2025学年北师大版(2019)必修第二册数学高一下册
文档属性
| 名称 | 【期末热点.重难点】任意角(含解析)2024-2025学年北师大版(2019)必修第二册数学高一下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 244.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-23 08:40:44 | ||
图片预览


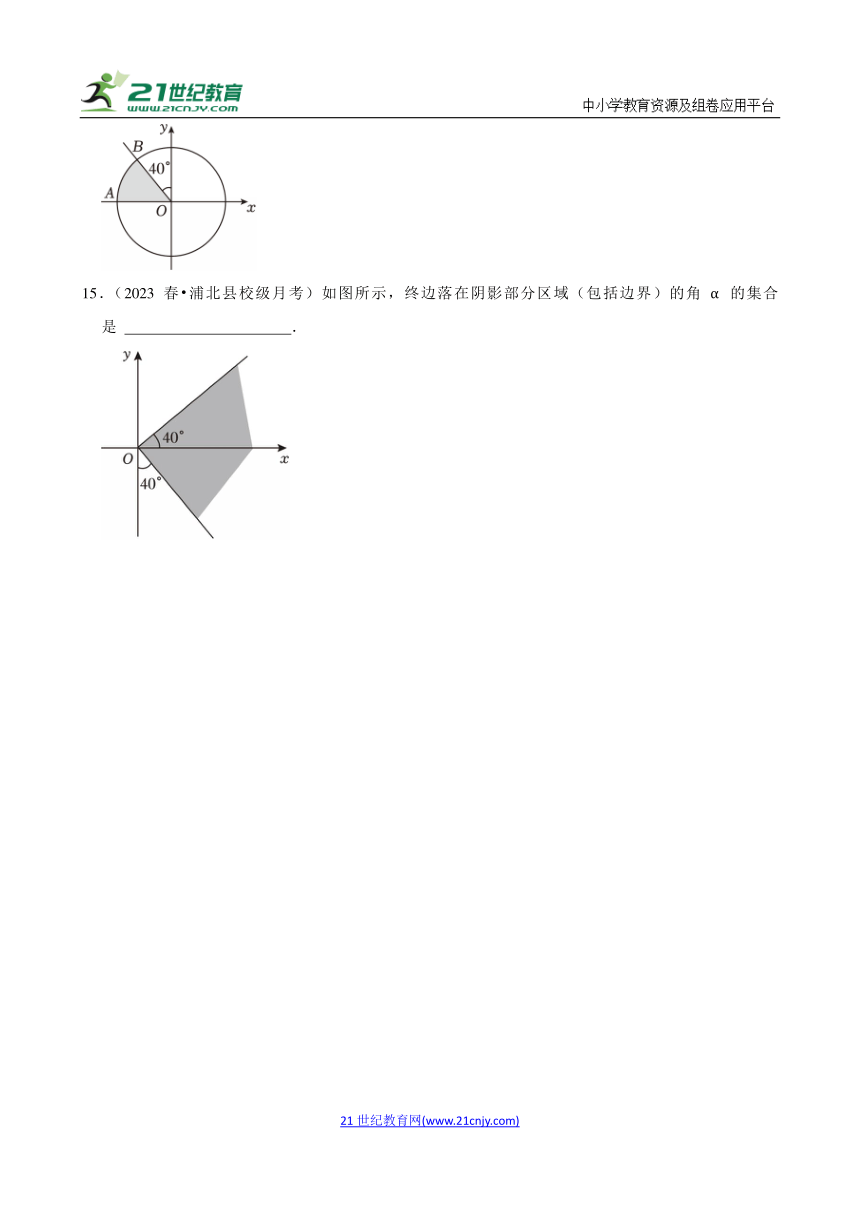


文档简介
期末热点.重难点 任意角
一.选择题(共5小题)
1.(2024秋 上城区校级期末)已知点P(sinα,cosα)是第四象限的点,则角α的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2024秋 花都区期末)若θ=2025°,则θ的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(2024秋 织金县期末)﹣1600°的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2024秋 榆林期末)是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
5.(2024秋 哈尔滨校级期末)已知角α=1370°,则角α的终边落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二.多选题(共4小题)
(多选)6.(2024秋 喀什市期末)已知α是第四象限角,则可能是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
(多选)7.(2024秋 杜集区校级期末)下列四个选项,正确的有( )
A.P(tanα,cosα)在第三象限,则α是第二象限角
B.若三角形的两内角A,B,满足sinAcosB<0,则此三角形必为钝角三角形
C.sin145°cos(﹣210°)>0
D.sin3 cos4 tan5>0
(多选)8.(2024秋 辛集市期末)下列说法正确的有( )
A.θ为第三象限角的充要条件为sinθtanθ<0
B.若θ为第二象限角,则为第一或第三象限角
C.
D.sin(﹣1071°)sin99°+sin(﹣171°)sin(﹣261°)=0
(多选)9.(2024秋 江门期末)下列说法正确的是( )
A.钝角都是第二象限角
B.第二象限角大于第一象限角
C.终边落在y轴上的角的集合可表示为
D.若sinx﹣cosx>0,则
三.填空题(共3小题)
10.(2024秋 上海校级期末)已知α是第二象限角,则终边在第 象限.
11.(2024秋 浦东新区校级期末)2024°角的终边在第 象限.
12.(2024秋 浦东新区校级期末)顶点在平面直角坐标系的原点,始边与x轴的正半轴重合,2025°的角属于第 象限.
四.解答题(共3小题)
13.(2024春 余干县校级月考)用弧度制写出终边在阴影部分的角的集合:
14.(2023秋 偃师区校级月考)如图,将圆O放在平面直角坐标系中,圆心与原点重合.
(1)如何表示图中终边落在射线OB上的角?
(2)如何表示终边落在图中阴影区域角φ的范围?
(3)对顶区域的角如何表示?
15.(2023春 浦北县校级月考)如图所示,终边落在阴影部分区域(包括边界)的角α的集合是 .
期末热点.重难点 任意角
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 上城区校级期末)已知点P(sinα,cosα)是第四象限的点,则角α的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】象限角、轴线角.
【专题】转化思想;转化法;三角函数的求值;运算求解.
【答案】B
【分析】先根据点P所在的象限,判断sinα,cosα的符号,再结合各象限三角函数的符号,确定角α终边所在的位置.
【解答】解:由题意可知,sinα>0且cosα<0.
所以角α的终边位于第二象限.
故选:B.
【点评】本题主要考查象限角,属于基础题.
2.(2024秋 花都区期末)若θ=2025°,则θ的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】象限角、轴线角.
【专题】计算题;转化思想;综合法;三角函数的求值;逻辑思维;运算求解.
【答案】C
【分析】根据终边相同的角和象限角的定义计算.
【解答】解:因为2025°=5×360°+225°,易知225°的终边在第三象限.
故选:C.
【点评】本题考查的知识点:象限角的定义,主要考查学生的运算能力,属于基础题.
3.(2024秋 织金县期末)﹣1600°的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】象限角、轴线角.
【专题】转化思想;转化法;三角函数的求值;运算求解.
【答案】C
【分析】根据已知条件,结合象限角的定义,即可求解.
【解答】解:﹣1600°=(﹣5)×360°+200°,
故﹣1600°的终边在第三象限.
故选:C.
【点评】本题主要考查象限角的定义,属于基础题.
4.(2024秋 榆林期末)是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】C
【分析】根据终边判断角的象限即可.
【解答】解:,是第三象限角,
与终边相同,
所以是第三象限角.
故选:C.
【点评】本题考查终边相同角的判断,属于基础题.
5.(2024秋 哈尔滨校级期末)已知角α=1370°,则角α的终边落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】D
【分析】求出α与290°的角终边相同,从而得到答案.
【解答】解:因为α=1370°=360°×3+290°,
又290°是第四象限角,故角α的终边落在第四象限.
故选:D.
【点评】本题考查了象限角的判断,属于基础题.
二.多选题(共4小题)
(多选)6.(2024秋 喀什市期末)已知α是第四象限角,则可能是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的图象与性质;运算求解.
【答案】BD
【分析】根据象限角的性质即可求解.
【解答】解:根据题意,α是第四象限角,故,k∈Z,
所以,k∈Z,
若k是偶数,则为第二象限角,若k是奇数,则为第四象限角,
则第二象限角,第四象限角符合题意.
故选:BD.
【点评】本题考查了象限角,属于基础题.
(多选)7.(2024秋 杜集区校级期末)下列四个选项,正确的有( )
A.P(tanα,cosα)在第三象限,则α是第二象限角
B.若三角形的两内角A,B,满足sinAcosB<0,则此三角形必为钝角三角形
C.sin145°cos(﹣210°)>0
D.sin3 cos4 tan5>0
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】ABD
【分析】A.根据P(tanα,cosα)在第三象限,由判断;
B.根据A,B是三角形的内角,且sinAcosB<0判断;
C.利用诱导公式判断;
D.根据判断.
【解答】解:A.因为P(tanα,cosα)在第三象限,所以,则α是第二象限角,故A正确,
B.因为A,B是三角形的内角,且sinAcosB<0,sinA>0,cosB<0,则,所以此三角形必为钝角三角形,故B正确,
C.因为sin145°cos(﹣210°)=﹣sin35°cos150°<0,故C错误,
D.因为,所以sin3 cos4 tan5>0,故D正确.
故选:ABD.
【点评】本题考查了诱导公式,属于基础题.
(多选)8.(2024秋 辛集市期末)下列说法正确的有( )
A.θ为第三象限角的充要条件为sinθtanθ<0
B.若θ为第二象限角,则为第一或第三象限角
C.
D.sin(﹣1071°)sin99°+sin(﹣171°)sin(﹣261°)=0
【考点】象限角、轴线角;三角函数值的符号;运用诱导公式化简求值;三角函数的恒等变换及化简求值.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】BCD
【分析】利用三角函数角在各象限三角函数值的正负,以及角在各象限范围,诱导公式,同角三角函数基本关系,判断四个选项即可.
【解答】解:对于A,当θ为第三象限角时,sinθ<0,tanθ>0,所以sinθtanθ<0,
反之,当sinθtanθ<0时,则有
①当sinθ<0,tanθ>0,θ为第三象限角,
②当sinθ>0,tanθ<0时,θ为第二象限角,故A错误;
对于B,若θ为第二象限角,即,k∈Z,
则,k∈Z,则为第一或第三象限角,故B正确;
对于C,,故C正确;
对于D,sin(﹣1071°)sin99°+sin(﹣171°)sin(﹣261°)=﹣sin1071°sin99°+sin171°sin261°
=﹣sin(1080°﹣9°)sin(90°+9°)+sin(180°﹣9°)sin(180°+81°)
=sin9°cos9°﹣sin9°sin81°
=sin9°cos9°﹣sin9°cos9°=0,故D正确.
故选:BCD.
【点评】本题考查三角函数的诱导公式,同角三角函数基本关系,属于基础题.
(多选)9.(2024秋 江门期末)下列说法正确的是( )
A.钝角都是第二象限角
B.第二象限角大于第一象限角
C.终边落在y轴上的角的集合可表示为
D.若sinx﹣cosx>0,则
【考点】象限角、轴线角;正切函数的图象;任意角的概念;终边相同的角(弧度制).
【专题】计算题;转化思想;综合法;三角函数的求值;逻辑思维;运算求解.
【答案】ACD
【分析】直接利用象限角的定义,轴线角的定义,三角不等式的解法判断A、B、C、D的结论.
【解答】解:对于A:钝角都是第二象限角,故A正确;
对于B:第二象限角指的是终边落在第二象限的角,第一象限角指的是终边落在第一象限的角,不能比较大小,故B错误;
对于C:终边落在y轴上的角的集合为,故C正确;
对于D:若sinx﹣cosx>0,故,所以(k∈Z),
整理得:(k∈Z),故,故D正确.
故选:ACD.
【点评】本题考查的知识点:象限角的定义,轴线角的定义,三角不等式的解法,主要考查学生的运算能力,属于基础题.
三.填空题(共3小题)
10.(2024秋 上海校级期末)已知α是第二象限角,则终边在第 一或三 象限.
【考点】象限角、轴线角.
【专题】分类讨论;综合法;三角函数的求值;数学抽象.
【答案】一或三.
【分析】根据象限角的范围即可求出结果.
【解答】解:由题意知,
则,
当k=2n,n∈Z时,,
此时终边在第一象限,
当k=2n+1,n∈Z时,,
此时终边在第三象限.
所以终边在第一和三象限.
故答案为:一或三.
【点评】本题主要考查了象限角的判断,属于基础题.
11.(2024秋 浦东新区校级期末)2024°角的终边在第 三 象限.
【考点】象限角、轴线角;终边相同的角.
【专题】整体思想;综合法;三角函数的求值;数学抽象.
【答案】三.
【分析】结合终边相同角的表示及象限角的定义即可判断.
【解答】解:因为2024°=5×360°+224°,
因为224°为第三象限角,
故2024°角的终边在第三象限角.
故答案为:三.
【点评】本题主要考查了终边相同角的表示及象限角的判断,属于基础题.
12.(2024秋 浦东新区校级期末)顶点在平面直角坐标系的原点,始边与x轴的正半轴重合,2025°的角属于第 三 象限.
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】三.
【分析】利用终边相同角的定义即可判断.
【解答】解:因为2025°=5×360°+225°,且225°是第三象限角,
所以2025°是第三象限角.
故答案为:三.
【点评】本题考查了象限角的判断,属于基础题.
四.解答题(共3小题)
13.(2024春 余干县校级月考)用弧度制写出终边在阴影部分的角的集合:
【考点】象限角、轴线角.
【专题】集合思想;转化法;三角函数的求值;运算求解.
【答案】(1);
(2).
【分析】首先找到对应边界的终边表示的角,再写成集合形式.
【解答】解:(1)由图可知,边界对应射线所在终边的角分别为,,k∈Z,
终边在阴影部分的角的集合为{α|α,k∈Z};
(2)边界对应射线所在终边的角分别为2kπ,,2kπ+π,,k∈Z,
∴终边在阴影部分的角的集合为:
.
【点评】本题考查角的范围的表示方法,考查角度制与弧度制的转化,是基础题.
14.(2023秋 偃师区校级月考)如图,将圆O放在平面直角坐标系中,圆心与原点重合.
(1)如何表示图中终边落在射线OB上的角?
(2)如何表示终边落在图中阴影区域角φ的范围?
(3)对顶区域的角如何表示?
【考点】象限角、轴线角.
【专题】计算题;转化思想;综合法;三角函数的求值;逻辑思维;运算求解.
【答案】答案见解析.
【分析】(1)先求∠xOB=90°+40°=130°,再写终边落在射线OB上的角;
(2)用射线OB,OA上的角可表示;
(3)根据对顶区域的对应角相差k 180°(k∈Z)可得到.
【解答】解:(1)k 360°+130°,k∈Z.
(2)由题图可知k 360°+130°≤φ≤k 360°+180°,k∈Z.
(3)对顶区域,先写出在0°~180°范围内始边、终边对应的角,再加上k 180°(k∈Z),即得对顶区域角的范围.
【点评】本题考查了用不等式表示区域角,关键是用区域的边界上的角表示,属于基础题.
15.(2023春 浦北县校级月考)如图所示,终边落在阴影部分区域(包括边界)的角α的集合是 {α|﹣50°+k 360°≤α≤40°+k 360°,k∈Z} .
【考点】象限角、轴线角.
【专题】数形结合;综合法;三角函数的求值;运算求解.
【答案】{α|﹣50°+k 360°≤α≤40°+k 360°,k∈Z}.
【分析】根据终边相同的角的集合得出分别与角40°,﹣50°终边相同的角即可.
【解答】解:分别与角40°,﹣50°终边相同的角为40°+k 360°,﹣50°+k 360°(k∈Z).
因此终边落在阴影区域(包括边界)的角的集合是{α|﹣50°+k 360°≤α≤40°+k 360°,k∈Z}.
故答案为:{α|﹣50°+k 360°≤α≤40°+k 360°,k∈Z}.
【点评】本题考查了终边相同的角的集合,属于基础题.
21世纪教育网(www.21cnjy.com)
一.选择题(共5小题)
1.(2024秋 上城区校级期末)已知点P(sinα,cosα)是第四象限的点,则角α的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2024秋 花都区期末)若θ=2025°,则θ的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(2024秋 织金县期末)﹣1600°的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2024秋 榆林期末)是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
5.(2024秋 哈尔滨校级期末)已知角α=1370°,则角α的终边落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二.多选题(共4小题)
(多选)6.(2024秋 喀什市期末)已知α是第四象限角,则可能是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
(多选)7.(2024秋 杜集区校级期末)下列四个选项,正确的有( )
A.P(tanα,cosα)在第三象限,则α是第二象限角
B.若三角形的两内角A,B,满足sinAcosB<0,则此三角形必为钝角三角形
C.sin145°cos(﹣210°)>0
D.sin3 cos4 tan5>0
(多选)8.(2024秋 辛集市期末)下列说法正确的有( )
A.θ为第三象限角的充要条件为sinθtanθ<0
B.若θ为第二象限角,则为第一或第三象限角
C.
D.sin(﹣1071°)sin99°+sin(﹣171°)sin(﹣261°)=0
(多选)9.(2024秋 江门期末)下列说法正确的是( )
A.钝角都是第二象限角
B.第二象限角大于第一象限角
C.终边落在y轴上的角的集合可表示为
D.若sinx﹣cosx>0,则
三.填空题(共3小题)
10.(2024秋 上海校级期末)已知α是第二象限角,则终边在第 象限.
11.(2024秋 浦东新区校级期末)2024°角的终边在第 象限.
12.(2024秋 浦东新区校级期末)顶点在平面直角坐标系的原点,始边与x轴的正半轴重合,2025°的角属于第 象限.
四.解答题(共3小题)
13.(2024春 余干县校级月考)用弧度制写出终边在阴影部分的角的集合:
14.(2023秋 偃师区校级月考)如图,将圆O放在平面直角坐标系中,圆心与原点重合.
(1)如何表示图中终边落在射线OB上的角?
(2)如何表示终边落在图中阴影区域角φ的范围?
(3)对顶区域的角如何表示?
15.(2023春 浦北县校级月考)如图所示,终边落在阴影部分区域(包括边界)的角α的集合是 .
期末热点.重难点 任意角
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 上城区校级期末)已知点P(sinα,cosα)是第四象限的点,则角α的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】象限角、轴线角.
【专题】转化思想;转化法;三角函数的求值;运算求解.
【答案】B
【分析】先根据点P所在的象限,判断sinα,cosα的符号,再结合各象限三角函数的符号,确定角α终边所在的位置.
【解答】解:由题意可知,sinα>0且cosα<0.
所以角α的终边位于第二象限.
故选:B.
【点评】本题主要考查象限角,属于基础题.
2.(2024秋 花都区期末)若θ=2025°,则θ的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】象限角、轴线角.
【专题】计算题;转化思想;综合法;三角函数的求值;逻辑思维;运算求解.
【答案】C
【分析】根据终边相同的角和象限角的定义计算.
【解答】解:因为2025°=5×360°+225°,易知225°的终边在第三象限.
故选:C.
【点评】本题考查的知识点:象限角的定义,主要考查学生的运算能力,属于基础题.
3.(2024秋 织金县期末)﹣1600°的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】象限角、轴线角.
【专题】转化思想;转化法;三角函数的求值;运算求解.
【答案】C
【分析】根据已知条件,结合象限角的定义,即可求解.
【解答】解:﹣1600°=(﹣5)×360°+200°,
故﹣1600°的终边在第三象限.
故选:C.
【点评】本题主要考查象限角的定义,属于基础题.
4.(2024秋 榆林期末)是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】C
【分析】根据终边判断角的象限即可.
【解答】解:,是第三象限角,
与终边相同,
所以是第三象限角.
故选:C.
【点评】本题考查终边相同角的判断,属于基础题.
5.(2024秋 哈尔滨校级期末)已知角α=1370°,则角α的终边落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】D
【分析】求出α与290°的角终边相同,从而得到答案.
【解答】解:因为α=1370°=360°×3+290°,
又290°是第四象限角,故角α的终边落在第四象限.
故选:D.
【点评】本题考查了象限角的判断,属于基础题.
二.多选题(共4小题)
(多选)6.(2024秋 喀什市期末)已知α是第四象限角,则可能是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的图象与性质;运算求解.
【答案】BD
【分析】根据象限角的性质即可求解.
【解答】解:根据题意,α是第四象限角,故,k∈Z,
所以,k∈Z,
若k是偶数,则为第二象限角,若k是奇数,则为第四象限角,
则第二象限角,第四象限角符合题意.
故选:BD.
【点评】本题考查了象限角,属于基础题.
(多选)7.(2024秋 杜集区校级期末)下列四个选项,正确的有( )
A.P(tanα,cosα)在第三象限,则α是第二象限角
B.若三角形的两内角A,B,满足sinAcosB<0,则此三角形必为钝角三角形
C.sin145°cos(﹣210°)>0
D.sin3 cos4 tan5>0
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】ABD
【分析】A.根据P(tanα,cosα)在第三象限,由判断;
B.根据A,B是三角形的内角,且sinAcosB<0判断;
C.利用诱导公式判断;
D.根据判断.
【解答】解:A.因为P(tanα,cosα)在第三象限,所以,则α是第二象限角,故A正确,
B.因为A,B是三角形的内角,且sinAcosB<0,sinA>0,cosB<0,则,所以此三角形必为钝角三角形,故B正确,
C.因为sin145°cos(﹣210°)=﹣sin35°cos150°<0,故C错误,
D.因为,所以sin3 cos4 tan5>0,故D正确.
故选:ABD.
【点评】本题考查了诱导公式,属于基础题.
(多选)8.(2024秋 辛集市期末)下列说法正确的有( )
A.θ为第三象限角的充要条件为sinθtanθ<0
B.若θ为第二象限角,则为第一或第三象限角
C.
D.sin(﹣1071°)sin99°+sin(﹣171°)sin(﹣261°)=0
【考点】象限角、轴线角;三角函数值的符号;运用诱导公式化简求值;三角函数的恒等变换及化简求值.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】BCD
【分析】利用三角函数角在各象限三角函数值的正负,以及角在各象限范围,诱导公式,同角三角函数基本关系,判断四个选项即可.
【解答】解:对于A,当θ为第三象限角时,sinθ<0,tanθ>0,所以sinθtanθ<0,
反之,当sinθtanθ<0时,则有
①当sinθ<0,tanθ>0,θ为第三象限角,
②当sinθ>0,tanθ<0时,θ为第二象限角,故A错误;
对于B,若θ为第二象限角,即,k∈Z,
则,k∈Z,则为第一或第三象限角,故B正确;
对于C,,故C正确;
对于D,sin(﹣1071°)sin99°+sin(﹣171°)sin(﹣261°)=﹣sin1071°sin99°+sin171°sin261°
=﹣sin(1080°﹣9°)sin(90°+9°)+sin(180°﹣9°)sin(180°+81°)
=sin9°cos9°﹣sin9°sin81°
=sin9°cos9°﹣sin9°cos9°=0,故D正确.
故选:BCD.
【点评】本题考查三角函数的诱导公式,同角三角函数基本关系,属于基础题.
(多选)9.(2024秋 江门期末)下列说法正确的是( )
A.钝角都是第二象限角
B.第二象限角大于第一象限角
C.终边落在y轴上的角的集合可表示为
D.若sinx﹣cosx>0,则
【考点】象限角、轴线角;正切函数的图象;任意角的概念;终边相同的角(弧度制).
【专题】计算题;转化思想;综合法;三角函数的求值;逻辑思维;运算求解.
【答案】ACD
【分析】直接利用象限角的定义,轴线角的定义,三角不等式的解法判断A、B、C、D的结论.
【解答】解:对于A:钝角都是第二象限角,故A正确;
对于B:第二象限角指的是终边落在第二象限的角,第一象限角指的是终边落在第一象限的角,不能比较大小,故B错误;
对于C:终边落在y轴上的角的集合为,故C正确;
对于D:若sinx﹣cosx>0,故,所以(k∈Z),
整理得:(k∈Z),故,故D正确.
故选:ACD.
【点评】本题考查的知识点:象限角的定义,轴线角的定义,三角不等式的解法,主要考查学生的运算能力,属于基础题.
三.填空题(共3小题)
10.(2024秋 上海校级期末)已知α是第二象限角,则终边在第 一或三 象限.
【考点】象限角、轴线角.
【专题】分类讨论;综合法;三角函数的求值;数学抽象.
【答案】一或三.
【分析】根据象限角的范围即可求出结果.
【解答】解:由题意知,
则,
当k=2n,n∈Z时,,
此时终边在第一象限,
当k=2n+1,n∈Z时,,
此时终边在第三象限.
所以终边在第一和三象限.
故答案为:一或三.
【点评】本题主要考查了象限角的判断,属于基础题.
11.(2024秋 浦东新区校级期末)2024°角的终边在第 三 象限.
【考点】象限角、轴线角;终边相同的角.
【专题】整体思想;综合法;三角函数的求值;数学抽象.
【答案】三.
【分析】结合终边相同角的表示及象限角的定义即可判断.
【解答】解:因为2024°=5×360°+224°,
因为224°为第三象限角,
故2024°角的终边在第三象限角.
故答案为:三.
【点评】本题主要考查了终边相同角的表示及象限角的判断,属于基础题.
12.(2024秋 浦东新区校级期末)顶点在平面直角坐标系的原点,始边与x轴的正半轴重合,2025°的角属于第 三 象限.
【考点】象限角、轴线角.
【专题】转化思想;综合法;三角函数的求值;运算求解.
【答案】三.
【分析】利用终边相同角的定义即可判断.
【解答】解:因为2025°=5×360°+225°,且225°是第三象限角,
所以2025°是第三象限角.
故答案为:三.
【点评】本题考查了象限角的判断,属于基础题.
四.解答题(共3小题)
13.(2024春 余干县校级月考)用弧度制写出终边在阴影部分的角的集合:
【考点】象限角、轴线角.
【专题】集合思想;转化法;三角函数的求值;运算求解.
【答案】(1);
(2).
【分析】首先找到对应边界的终边表示的角,再写成集合形式.
【解答】解:(1)由图可知,边界对应射线所在终边的角分别为,,k∈Z,
终边在阴影部分的角的集合为{α|α,k∈Z};
(2)边界对应射线所在终边的角分别为2kπ,,2kπ+π,,k∈Z,
∴终边在阴影部分的角的集合为:
.
【点评】本题考查角的范围的表示方法,考查角度制与弧度制的转化,是基础题.
14.(2023秋 偃师区校级月考)如图,将圆O放在平面直角坐标系中,圆心与原点重合.
(1)如何表示图中终边落在射线OB上的角?
(2)如何表示终边落在图中阴影区域角φ的范围?
(3)对顶区域的角如何表示?
【考点】象限角、轴线角.
【专题】计算题;转化思想;综合法;三角函数的求值;逻辑思维;运算求解.
【答案】答案见解析.
【分析】(1)先求∠xOB=90°+40°=130°,再写终边落在射线OB上的角;
(2)用射线OB,OA上的角可表示;
(3)根据对顶区域的对应角相差k 180°(k∈Z)可得到.
【解答】解:(1)k 360°+130°,k∈Z.
(2)由题图可知k 360°+130°≤φ≤k 360°+180°,k∈Z.
(3)对顶区域,先写出在0°~180°范围内始边、终边对应的角,再加上k 180°(k∈Z),即得对顶区域角的范围.
【点评】本题考查了用不等式表示区域角,关键是用区域的边界上的角表示,属于基础题.
15.(2023春 浦北县校级月考)如图所示,终边落在阴影部分区域(包括边界)的角α的集合是 {α|﹣50°+k 360°≤α≤40°+k 360°,k∈Z} .
【考点】象限角、轴线角.
【专题】数形结合;综合法;三角函数的求值;运算求解.
【答案】{α|﹣50°+k 360°≤α≤40°+k 360°,k∈Z}.
【分析】根据终边相同的角的集合得出分别与角40°,﹣50°终边相同的角即可.
【解答】解:分别与角40°,﹣50°终边相同的角为40°+k 360°,﹣50°+k 360°(k∈Z).
因此终边落在阴影区域(包括边界)的角的集合是{α|﹣50°+k 360°≤α≤40°+k 360°,k∈Z}.
故答案为:{α|﹣50°+k 360°≤α≤40°+k 360°,k∈Z}.
【点评】本题考查了终边相同的角的集合,属于基础题.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
