20_1_1_1平均数 (主题情境:招聘翻译精英)【2025春人教八下数学情境课堂课件】 共32张PPT
文档属性
| 名称 | 20_1_1_1平均数 (主题情境:招聘翻译精英)【2025春人教八下数学情境课堂课件】 共32张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 22:06:40 | ||
图片预览










文档简介
(共32张PPT)
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
20.1 数据的集中趋势
20.1.1.1 平均数
第20章 数据分析
主题情境·招聘翻译精英
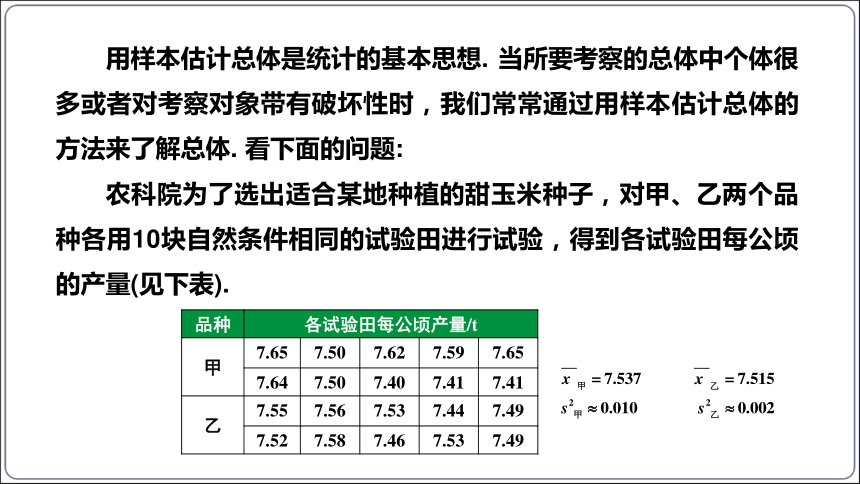
用样本估计总体是统计的基本思想. 当所要考察的总体中个体很多或者对考察对象带有破坏性时,我们常常通过用样本估计总体的方法来了解总体. 看下面的问题:
农科院为了选出适合某地种植的甜玉米种子,对甲、乙两个品种各用10块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(见下表).
品种 各试验田每公顷产量/t 甲 7.65 7.50 7.62 7.59 7.65
7.64 7.50 7.40 7.41 7.41
乙 7.55 7.56 7.53 7.44 7.49
7.52 7.58 7.46 7.53 7.49
根据这些数据,应为农科院选择甜玉米种子提出怎样的建议呢
甜玉米的产量和产量的稳定性是农科院选择种子时所关心的问题. 如何考察一种甜玉米的产量和产量的稳定性呢 这要用到本章将要学习的如何用样本的平均数和方差估计总体的平均数和方差等知识.
通过本章的学习,你将对数据的作用有更多的认识,对用样本估计总体的思想有更深的体会.
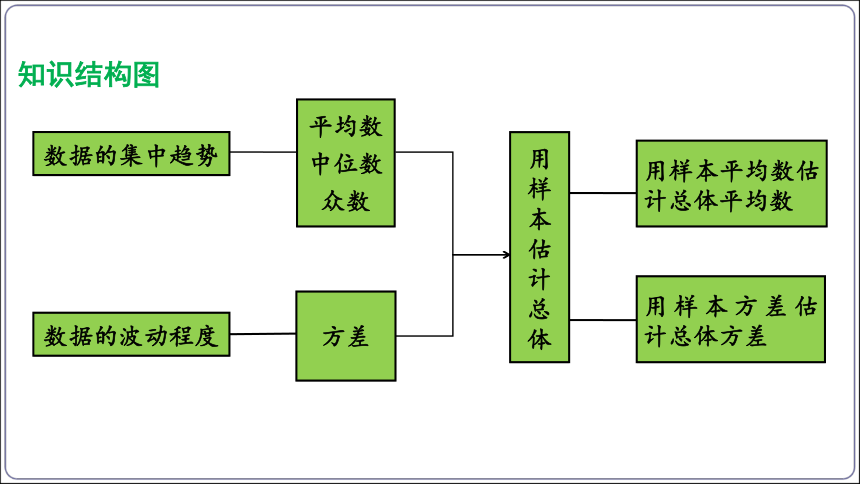
知识结构图
数据的集中趋势
用样本平均数估计总体平均数
数据的波动程度
平均数
中位数
众数
方差
用样本估计总体
用样本方差估计总体方差
教材前后关联
数据的收集、整理为数据的分析提供了必要的基础知识和技能,而数据的分析则在数据的收集、整理的基础上进行了扩展和应用
人教八下
人教七下
教材前后关联
数据的分析为概率的初步学习提供了必要的基础知识和思维训练,因为概率论本质上是研究随机现象中事件发生的可能性,而这种可能性往往通过数据分析来估计和验证
人教八下
人教九上
中考考查情况
本章在中考选择填空题中直接考查中位数或众数的计算或意义.
在数据的统计与分析综合题中主要考查:
①直接给出数据或结合统计图表计算平均数、中位数或众数,并能利用样本估计整体思想对整体情况进行评价;
②考查中位数、众数或方差的意义,能根据具体需求选择适当的统计量对数据的集中趋势做出判断.
学习目标
1. 经历用平均数描述数据集中趋势的过程.
2. 理解算术平均数、加权平均数的概念.
3. 会求一组数据的算术平均数和加权平均数,并解决相关问题.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
以下是甲、乙两名应试者进行听、说、读、写水平测试的各项成绩(百分制)如表所示:
情境学新知
一家公司打算招聘一名英文翻译. 公司在初试设置了全面英语能力测评环节!此环节,我们将通过听、说、读、写四个方面的全方位测试,综合评估并挑选出具备优秀英语口语能力和翻译能力的候选人.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
问题1 如果公司想招一名综合能力较强的翻译,谁能通过初试?你是怎样判断的?
显然甲的平均成绩比乙高,所以从成绩看,甲通过初试.
乙的平均成绩为
解:根据平均数公式,甲的平均成绩为
算术平均数
我们常用平均数表示一组数据的“平均水平”.
思考1 你还能回忆、归纳出算术平均数的概念吗?
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数.
问题2 如果公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:1:3:4的比确定,从他们的成绩看谁能通过初试?你是怎样判断的?
不合理,因为每一项的重要程度不一样!
还用算术平均数来衡量他们的成绩合理吗?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
各项成绩的重要程度有所不同,读、写的成绩比听、说的成绩更加“重要”.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
2 : 1 : 3 : 4
解:甲的平均成绩为
乙的平均成绩为
因为乙的成绩比甲高,所以乙通过初试.
问题1是利用平均数的公式计算平均成绩,其中的每个数据被认为同等重要.
问题2是根据实际需要对不同类型的数据赋予与其重要程度相应的比重,其中的2,1,3,4分别称为听、说、读、写四项成绩的权,相应的平均数79.5,80.4分别称为甲和乙的听、说、读、写四项成绩的加权平均数.
加权平均数
= 79.5,
权
一般地,若 n 个数 x1,x2,…,xn 的权分别是 w1,w2,…,wn,则
叫做这 n 个数的加权平均数.
加权平均数的作用:
当一组数据中各个数据的重要程度不同时,加权平均数能更好地反映这组数据的平均水平.
问题3 如果这家公司想招一名口语能力较强的翻译,各项成绩均按百分制计,其中听占30%、说占30%、读占20%、写占20%,那么甲、乙两人谁将通过初试?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
30% 30% 20% 20%
分析:这个问题可以看成是求两名应试者四项成绩的加权平均数,30%,30%,20%,20%说明听、说、读、写四项成绩在总成绩中的重要程度,是四项成绩的权.
解:甲的平均成绩为
乙的平均成绩为
因为甲的成绩比乙高,所以甲将通过初试.
问题3 如果这家公司想招一名口语能力较强的翻译,各项成绩均按百分制计,其中听占30%、说占30%、读占20%、写占20%,那么甲、乙两人谁将通过初试?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
30% 30% 20% 20%
思考2 比较问题1、问题2、问题3,你能体会到权的作用吗?
思考3 在问题2 和问题3 中,听、说、读、写四项成绩的权是以什么形式给出的?
数据的权能够反映数据的相对重要程度!
同样一张应试者的应聘成绩单,由于各个数据所赋的权重不同,造成的录取结果截然不同.
以比例的形式给出,如 2:1:3:4 .
以百分数的形式给出,如 30%,30%,20%,20% .
问题4 在招聘过程中,考虑到工作经验和职业稳定性,公司对2024年5、6月份所有参加初试的应聘者进行了年龄调查,结果如下:24岁11人,25岁8人,26岁5人,28岁3人,29岁1人. 求参加初试的应聘者的平均年龄(结果取整数).
解:参加初试的应聘者平均年龄为
在求n个数的平均数时,如果 x1 出现 f1 次,x2 出现 f2 次,…,xk 出现fk 次 (这里 f1+f2+ ... +fk=n),那么这 n 个数的平均数
也叫做 x1,x2,…,xk 这 k 个数的加权平均数,其中 f1,f2,…,fk分别叫做 x1,x2,…,xk 的权.
思考4 你能说说算术平均数与加权平均数的关系吗?
(1)联系:如果一组数据中各个数据重要程度相同,即 w1 = w2 = … = wn.
不妨设 w1 = w2 = … = wn = w,则
所以,算术平均数是加权平均数的一种特殊形式.
(2)区别:在实际问题中,当各项的权不相等时,计算平均数时就要采
用加权平均数;
当各项的权相等时,计算平均数就要采用算术平均数.
1.(2024南充)学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占60%,投球技能占40%计算选手的综合成绩(百分制). 选手李林控球技能得90分,投球技能得80分.李林综合成绩为( )
A.170分 B.86分 C.85分 D.84分
B
随堂练习
2. 小明参加“弘扬雷锋精神,争做美德少年”为主题的演讲比赛,其演讲形象、内容、效果三项得分分别是9分、8分、8分.若将三项得分依次按3∶4∶3的比例确定最终成绩,则小明的最终比赛成绩为_______分.
8.3
3.(2024德阳)某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占30%,面试占30%,试讲占40%进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为 ________ 分.
85.8
24
4. 现有甲、乙两种糖果的单价与千克数如下表所示.
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为________元/千克.
甲种糖果 乙种糖果
单价(元/千克) 30 20
千克数 2 3
5.(2024福建)已知A、B两地都只有甲、乙两类普通高中学校,在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分;乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
解:(1)由题意,得A地考生的数学平均分为
(2) 若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据
此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明;若不能,请举例说明.
解:(2)不能.
举例如下:如B地甲类学校有考生1 000人,乙类学校有考生3 000人,则B地考生的数学平均分为
因为85<86,所以不能判断B地考生数学平均分一定比A地考生数学平均分高.
注:本题答案不唯一,只要能作出正确判断,并且所举的例子能说明其判断即可.
算术平均数
平均数
加权平均数
当一组数据中各个数据重要程度不同时,加权平均数能更好地反映这组数据的平均水平.
一般地,若 n 个数 x1,x2,…,xn 的权分别是 w1,w2,…,wn,则
叫做这 n 个数的加权平均数.
加权平均数作用
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步精品课件
人教版八年级下册
2025年春八下数学情境课堂课件
20.1 数据的集中趋势
20.1.1.1 平均数
第20章 数据分析
主题情境·招聘翻译精英
用样本估计总体是统计的基本思想. 当所要考察的总体中个体很多或者对考察对象带有破坏性时,我们常常通过用样本估计总体的方法来了解总体. 看下面的问题:
农科院为了选出适合某地种植的甜玉米种子,对甲、乙两个品种各用10块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(见下表).
品种 各试验田每公顷产量/t 甲 7.65 7.50 7.62 7.59 7.65
7.64 7.50 7.40 7.41 7.41
乙 7.55 7.56 7.53 7.44 7.49
7.52 7.58 7.46 7.53 7.49
根据这些数据,应为农科院选择甜玉米种子提出怎样的建议呢
甜玉米的产量和产量的稳定性是农科院选择种子时所关心的问题. 如何考察一种甜玉米的产量和产量的稳定性呢 这要用到本章将要学习的如何用样本的平均数和方差估计总体的平均数和方差等知识.
通过本章的学习,你将对数据的作用有更多的认识,对用样本估计总体的思想有更深的体会.
知识结构图
数据的集中趋势
用样本平均数估计总体平均数
数据的波动程度
平均数
中位数
众数
方差
用样本估计总体
用样本方差估计总体方差
教材前后关联
数据的收集、整理为数据的分析提供了必要的基础知识和技能,而数据的分析则在数据的收集、整理的基础上进行了扩展和应用
人教八下
人教七下
教材前后关联
数据的分析为概率的初步学习提供了必要的基础知识和思维训练,因为概率论本质上是研究随机现象中事件发生的可能性,而这种可能性往往通过数据分析来估计和验证
人教八下
人教九上
中考考查情况
本章在中考选择填空题中直接考查中位数或众数的计算或意义.
在数据的统计与分析综合题中主要考查:
①直接给出数据或结合统计图表计算平均数、中位数或众数,并能利用样本估计整体思想对整体情况进行评价;
②考查中位数、众数或方差的意义,能根据具体需求选择适当的统计量对数据的集中趋势做出判断.
学习目标
1. 经历用平均数描述数据集中趋势的过程.
2. 理解算术平均数、加权平均数的概念.
3. 会求一组数据的算术平均数和加权平均数,并解决相关问题.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
以下是甲、乙两名应试者进行听、说、读、写水平测试的各项成绩(百分制)如表所示:
情境学新知
一家公司打算招聘一名英文翻译. 公司在初试设置了全面英语能力测评环节!此环节,我们将通过听、说、读、写四个方面的全方位测试,综合评估并挑选出具备优秀英语口语能力和翻译能力的候选人.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
问题1 如果公司想招一名综合能力较强的翻译,谁能通过初试?你是怎样判断的?
显然甲的平均成绩比乙高,所以从成绩看,甲通过初试.
乙的平均成绩为
解:根据平均数公式,甲的平均成绩为
算术平均数
我们常用平均数表示一组数据的“平均水平”.
思考1 你还能回忆、归纳出算术平均数的概念吗?
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数.
问题2 如果公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:1:3:4的比确定,从他们的成绩看谁能通过初试?你是怎样判断的?
不合理,因为每一项的重要程度不一样!
还用算术平均数来衡量他们的成绩合理吗?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
各项成绩的重要程度有所不同,读、写的成绩比听、说的成绩更加“重要”.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
2 : 1 : 3 : 4
解:甲的平均成绩为
乙的平均成绩为
因为乙的成绩比甲高,所以乙通过初试.
问题1是利用平均数的公式计算平均成绩,其中的每个数据被认为同等重要.
问题2是根据实际需要对不同类型的数据赋予与其重要程度相应的比重,其中的2,1,3,4分别称为听、说、读、写四项成绩的权,相应的平均数79.5,80.4分别称为甲和乙的听、说、读、写四项成绩的加权平均数.
加权平均数
= 79.5,
权
一般地,若 n 个数 x1,x2,…,xn 的权分别是 w1,w2,…,wn,则
叫做这 n 个数的加权平均数.
加权平均数的作用:
当一组数据中各个数据的重要程度不同时,加权平均数能更好地反映这组数据的平均水平.
问题3 如果这家公司想招一名口语能力较强的翻译,各项成绩均按百分制计,其中听占30%、说占30%、读占20%、写占20%,那么甲、乙两人谁将通过初试?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
30% 30% 20% 20%
分析:这个问题可以看成是求两名应试者四项成绩的加权平均数,30%,30%,20%,20%说明听、说、读、写四项成绩在总成绩中的重要程度,是四项成绩的权.
解:甲的平均成绩为
乙的平均成绩为
因为甲的成绩比乙高,所以甲将通过初试.
问题3 如果这家公司想招一名口语能力较强的翻译,各项成绩均按百分制计,其中听占30%、说占30%、读占20%、写占20%,那么甲、乙两人谁将通过初试?
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
30% 30% 20% 20%
思考2 比较问题1、问题2、问题3,你能体会到权的作用吗?
思考3 在问题2 和问题3 中,听、说、读、写四项成绩的权是以什么形式给出的?
数据的权能够反映数据的相对重要程度!
同样一张应试者的应聘成绩单,由于各个数据所赋的权重不同,造成的录取结果截然不同.
以比例的形式给出,如 2:1:3:4 .
以百分数的形式给出,如 30%,30%,20%,20% .
问题4 在招聘过程中,考虑到工作经验和职业稳定性,公司对2024年5、6月份所有参加初试的应聘者进行了年龄调查,结果如下:24岁11人,25岁8人,26岁5人,28岁3人,29岁1人. 求参加初试的应聘者的平均年龄(结果取整数).
解:参加初试的应聘者平均年龄为
在求n个数的平均数时,如果 x1 出现 f1 次,x2 出现 f2 次,…,xk 出现fk 次 (这里 f1+f2+ ... +fk=n),那么这 n 个数的平均数
也叫做 x1,x2,…,xk 这 k 个数的加权平均数,其中 f1,f2,…,fk分别叫做 x1,x2,…,xk 的权.
思考4 你能说说算术平均数与加权平均数的关系吗?
(1)联系:如果一组数据中各个数据重要程度相同,即 w1 = w2 = … = wn.
不妨设 w1 = w2 = … = wn = w,则
所以,算术平均数是加权平均数的一种特殊形式.
(2)区别:在实际问题中,当各项的权不相等时,计算平均数时就要采
用加权平均数;
当各项的权相等时,计算平均数就要采用算术平均数.
1.(2024南充)学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占60%,投球技能占40%计算选手的综合成绩(百分制). 选手李林控球技能得90分,投球技能得80分.李林综合成绩为( )
A.170分 B.86分 C.85分 D.84分
B
随堂练习
2. 小明参加“弘扬雷锋精神,争做美德少年”为主题的演讲比赛,其演讲形象、内容、效果三项得分分别是9分、8分、8分.若将三项得分依次按3∶4∶3的比例确定最终成绩,则小明的最终比赛成绩为_______分.
8.3
3.(2024德阳)某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占30%,面试占30%,试讲占40%进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为 ________ 分.
85.8
24
4. 现有甲、乙两种糖果的单价与千克数如下表所示.
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为________元/千克.
甲种糖果 乙种糖果
单价(元/千克) 30 20
千克数 2 3
5.(2024福建)已知A、B两地都只有甲、乙两类普通高中学校,在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分;乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
解:(1)由题意,得A地考生的数学平均分为
(2) 若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据
此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明;若不能,请举例说明.
解:(2)不能.
举例如下:如B地甲类学校有考生1 000人,乙类学校有考生3 000人,则B地考生的数学平均分为
因为85<86,所以不能判断B地考生数学平均分一定比A地考生数学平均分高.
注:本题答案不唯一,只要能作出正确判断,并且所举的例子能说明其判断即可.
算术平均数
平均数
加权平均数
当一组数据中各个数据重要程度不同时,加权平均数能更好地反映这组数据的平均水平.
一般地,若 n 个数 x1,x2,…,xn 的权分别是 w1,w2,…,wn,则
叫做这 n 个数的加权平均数.
加权平均数作用
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
