2.4.1抛物线及其标准方程
图片预览





文档简介
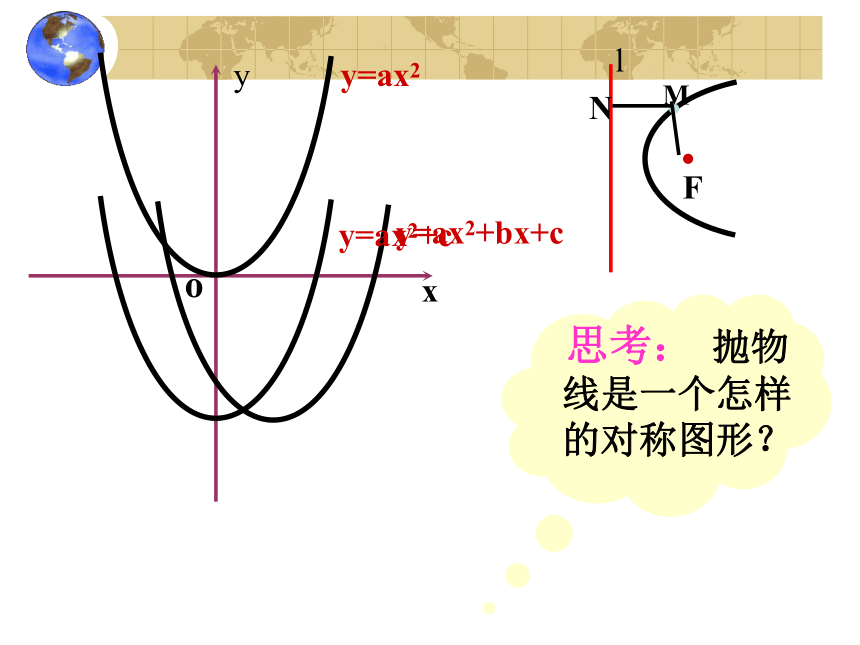
课件22张PPT。2.4.1抛物线及其标准方程请同学们思考两个问题1、我们对抛物线已有了哪些认识?2、二次函数的图像抛物线的
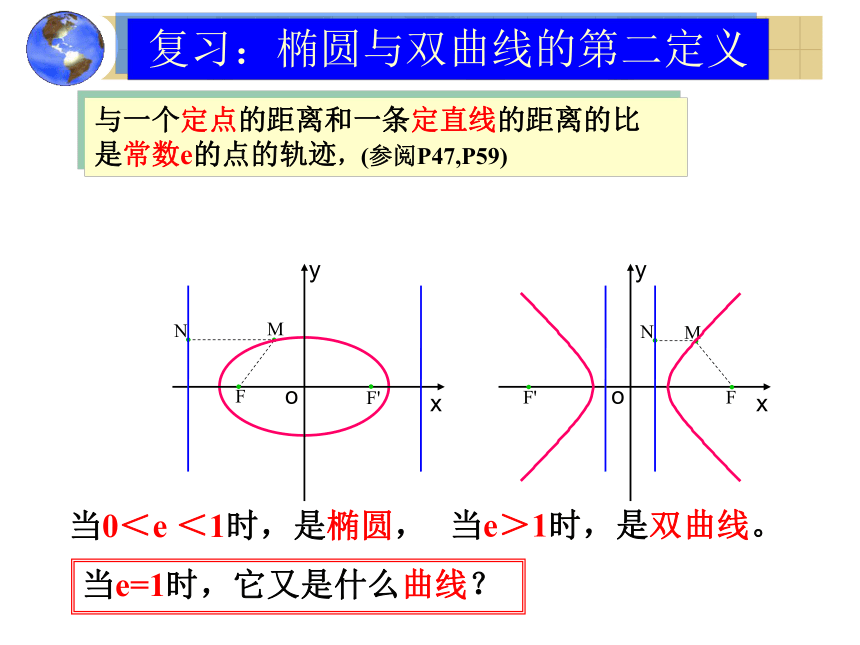
开口方向是什么? 在二次函数中研究的抛物线, 有开口向上或向下两种情形。复习:椭圆与双曲线的第二定义与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹,(参阅P47,P59)
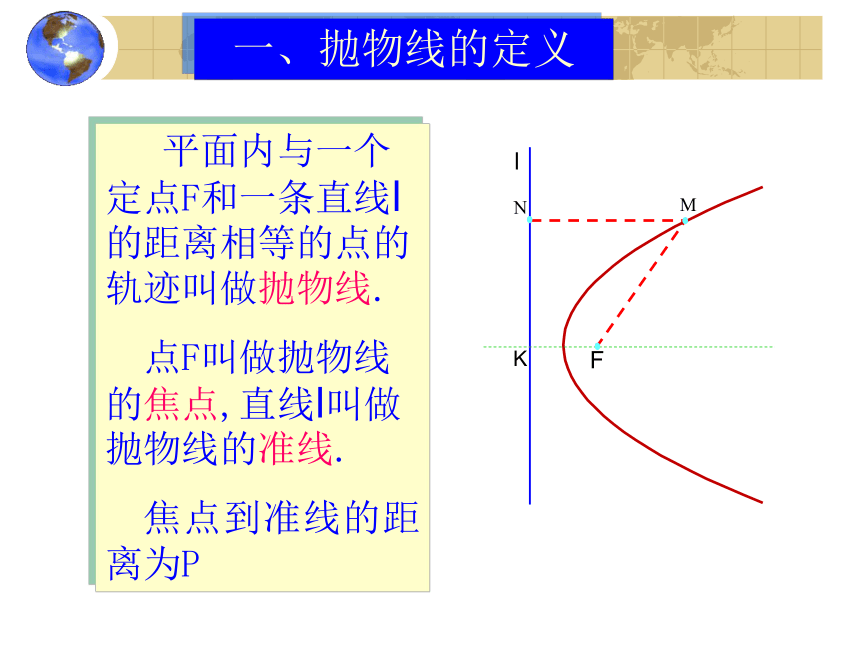
当0<e <1时,是椭圆,当e>1时,是双曲线。当e=1时,它又是什么曲线?一、抛物线的定义 平面内与一个定点F和一条直线l的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,直线l叫做抛物线的准线.
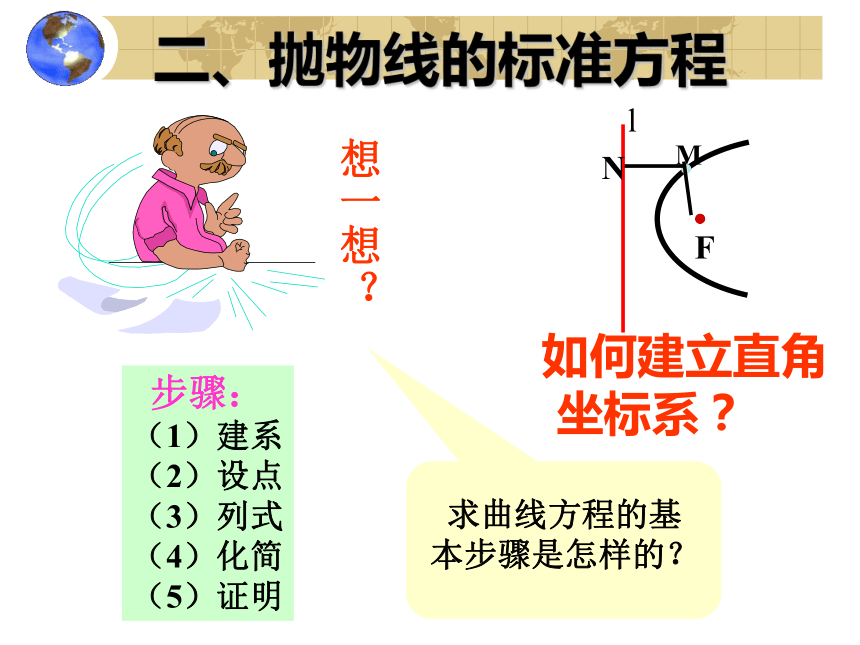
焦点到准线的距离为P二、抛物线的标准方程如何建立直角
坐标系?步骤:(1)建系(2)设点(3)列式(4)化简(5)证明二、标准方程K设︱KF︱= p(p>0)设点M的坐标为(x,y), 由定义可知,取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴 其中p为正常数,它的几何意义是
焦 点 到 准 线 的 距 离xyo抛物线的标准方程x2=2py(p>0)(0,p/2)y=-p/2y2=-2px
(p>0)(-p/2,0)x=p/2
x2=-2py
(p>0)(0,-p/2)y=p/2y2=2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,-p/2)(p/2,0)(-p/2,0)y=-p/2x=p/2x=-p/2抛物线的标准方程总结交流填表一次项看对称轴
正负看开口方向例1(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。三、例题讲解练习:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(3)焦点到准线的距离是2。y2 =12xy2 =xy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y(5,0)x= -5(0,-2)y=2例题讲解 例2. 已知抛物线经过点(-4,-2),求它的标准方程.解: (1)焦点在x轴上,设方程为
y2=-2px,(-4,-2)在抛物线上
有(-2)2=-2p(-4),解得p=1/2,
所求标准方程为y2=-x;
(2)焦点在y轴上,设标准方程为
x2=-2py, 可求方程为x2=-8y;
求过点A(-3,2)的抛物线的
标准方程。课堂练习变式训练1.根据下列条件写出抛物线的标准方程
(1)焦点是F(3,0);
(2)准线方程是x=1/4;
(3)焦点到准线的距离是2;
(4)焦点在直线3x-4y-12=0上.
2.求下列抛物线的焦点坐标与准线方程
(1)y2=28x;
(2)4x2=3y;
(3)2y2+5x=0;
(4)y=4ax2y2=12xy2=-xy2=4x或y2=-4x或x2=4y或x2=-4yy2=16x或x2=-12y焦点(7,0),准线x=-7焦点(0,1/16a),
准线y=-1/16a;
焦点(0,3/16),准线y=-3/16焦点(-5/8,0),准线x=5/8 课
堂
小
结抛物线的定义抛物线四种形式的标准方程抛物线的定义及其标准方程的简单应用椭圆与双曲线的第二定义数形结合的思想分类讨论的思想坐标法抛物线方程
左右型标准方程为
y2 =+ 2px
(p>0)开口向右:
y2 =2px(x≥ 0)开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)开口向上:
x2 =2py (y≥ 0)开口向下:
x2 = -2py (y≤0)抛物线的标准方程
上下型思考题、M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是
————————————二 次 函 数 的 最 值同学们再见!
开口方向是什么? 在二次函数中研究的抛物线, 有开口向上或向下两种情形。复习:椭圆与双曲线的第二定义与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹,(参阅P47,P59)
当0<e <1时,是椭圆,当e>1时,是双曲线。当e=1时,它又是什么曲线?一、抛物线的定义 平面内与一个定点F和一条直线l的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,直线l叫做抛物线的准线.
焦点到准线的距离为P二、抛物线的标准方程如何建立直角
坐标系?步骤:(1)建系(2)设点(3)列式(4)化简(5)证明二、标准方程K设︱KF︱= p(p>0)设点M的坐标为(x,y), 由定义可知,取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴 其中p为正常数,它的几何意义是
焦 点 到 准 线 的 距 离xyo抛物线的标准方程x2=2py(p>0)(0,p/2)y=-p/2y2=-2px
(p>0)(-p/2,0)x=p/2
x2=-2py
(p>0)(0,-p/2)y=p/2y2=2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,-p/2)(p/2,0)(-p/2,0)y=-p/2x=p/2x=-p/2抛物线的标准方程总结交流填表一次项看对称轴
正负看开口方向例1(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),
求它的标准方程。三、例题讲解练习:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(3)焦点到准线的距离是2。y2 =12xy2 =xy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y(5,0)x= -5(0,-2)y=2例题讲解 例2. 已知抛物线经过点(-4,-2),求它的标准方程.解: (1)焦点在x轴上,设方程为
y2=-2px,(-4,-2)在抛物线上
有(-2)2=-2p(-4),解得p=1/2,
所求标准方程为y2=-x;
(2)焦点在y轴上,设标准方程为
x2=-2py, 可求方程为x2=-8y;
求过点A(-3,2)的抛物线的
标准方程。课堂练习变式训练1.根据下列条件写出抛物线的标准方程
(1)焦点是F(3,0);
(2)准线方程是x=1/4;
(3)焦点到准线的距离是2;
(4)焦点在直线3x-4y-12=0上.
2.求下列抛物线的焦点坐标与准线方程
(1)y2=28x;
(2)4x2=3y;
(3)2y2+5x=0;
(4)y=4ax2y2=12xy2=-xy2=4x或y2=-4x或x2=4y或x2=-4yy2=16x或x2=-12y焦点(7,0),准线x=-7焦点(0,1/16a),
准线y=-1/16a;
焦点(0,3/16),准线y=-3/16焦点(-5/8,0),准线x=5/8 课
堂
小
结抛物线的定义抛物线四种形式的标准方程抛物线的定义及其标准方程的简单应用椭圆与双曲线的第二定义数形结合的思想分类讨论的思想坐标法抛物线方程
左右型标准方程为
y2 =+ 2px
(p>0)开口向右:
y2 =2px(x≥ 0)开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)开口向上:
x2 =2py (y≥ 0)开口向下:
x2 = -2py (y≤0)抛物线的标准方程
上下型思考题、M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是
————————————二 次 函 数 的 最 值同学们再见!
