16.1 轴对称 导学练课件(共38张PPT) 2025-2025学年冀教版八年级数学上册
文档属性
| 名称 | 16.1 轴对称 导学练课件(共38张PPT) 2025-2025学年冀教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 09:45:24 | ||
图片预览







文档简介
(共38张PPT)
16.1 轴对称
第十六章 轴对称和中心对称
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
轴对称图形
轴对称
成轴对称图形和轴对称图形的性质
画与一个图形成轴对称的图形
知1-讲
感悟新知
知识点
轴对称图形
1
1. 定义
一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴 .
感悟新知
知1-讲
特别解读
轴对称图形的三个条件:
(1)一个整体图形;
(2)一条直线——对称轴;
(3)直线两旁的部分沿直线对折后完全重合.
感悟新知
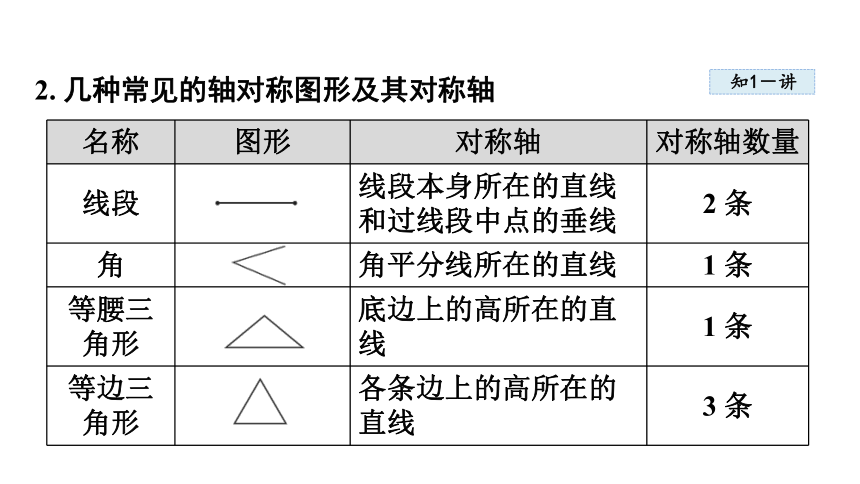
2. 几种常见的轴对称图形及其对称轴
知1-讲
名称 图形 对称轴 对称轴数量
线段 线段本身所在的直线和过线段中点的垂线 2 条
角 角平分线所在的直线 1 条
等腰三角形 底边上的高所在的直线 1 条
等边三角形 各条边上的高所在的直线 3 条
感悟新知
知1-讲
名称 图形 对称轴 对称轴数量
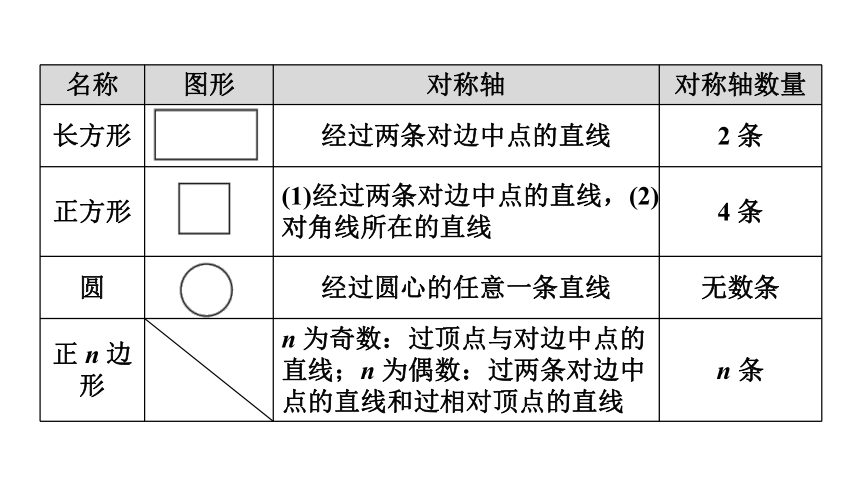
长方形 经过两条对边中点的直线 2 条
正方形 (1)经过两条对边中点的直线,(2)对角线所在的直线 4 条
圆 经过圆心的任意一条直线 无数条
正 n 边形 n 为奇数:过顶点与对边中点的直线;n 为偶数:过两条对边中点的直线和过相对顶点的直线 n 条
感悟新知
知1-讲
温馨提示
1. 轴对称图形是一个具有自身特性的图形,它被对称轴分成的两部分沿对称轴对折后能够互相重合,关于对称轴对称的点在同一图形上.
2. 对称轴是一条直线,而不是射线或线段.
3. 一个轴对称图形的对称轴可能有1 条,也可能有多条,还可能有无数条.
知1-练
感悟新知
人们常说:“地下文明看陕西,地上文明看山西.”山西素有“三晋古建甲天下”之称,下面是山西一些古城的图标设计图,其中不是轴对称图形的是( )
例1
考向:利用轴对称图形的定义识别轴对称图形
知1-练
感悟新知
解:A,B,D选项中的图标可以找到一条直线,使图标沿这条直线对折后直线两旁的部分能够完全重合,是轴对称图形,C 选项的图标不是轴对称图形.
解题秘方:根据轴对称图形的定义识别 .
答案:C
知1-练
感悟新知
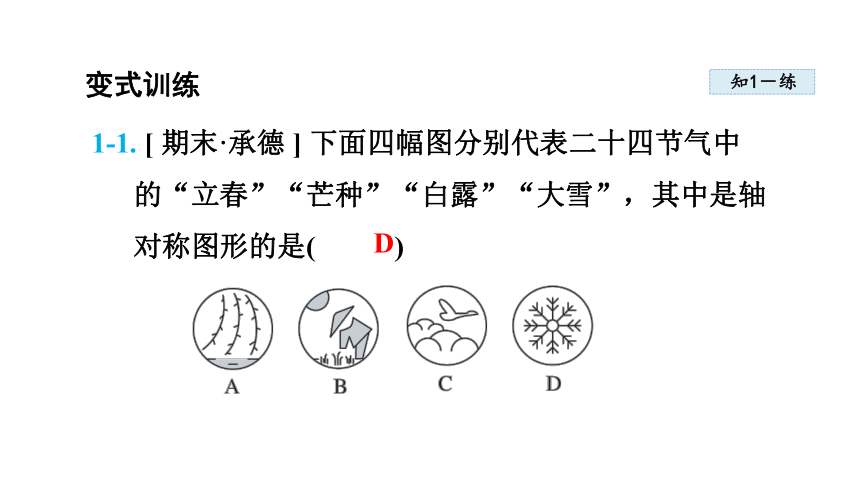
1-1. [ 期末·承德 ] 下面四幅图分别代表二十四节气中的“立春”“芒种”“白露”“大雪”,其中是轴对称图形的是( )
D
变式训练
感悟新知
知2-讲
知识点
轴对称
2
1. 定义
一般地,如果两个图形沿某条直线对折后能够完全重合,那么我们就称这两个图形成轴对称,这条直线叫作对称轴. 关于对称轴对称的点、对称的线段、对称的角分别叫作对应点、对应线段、对应角.
感悟新知
知2-讲
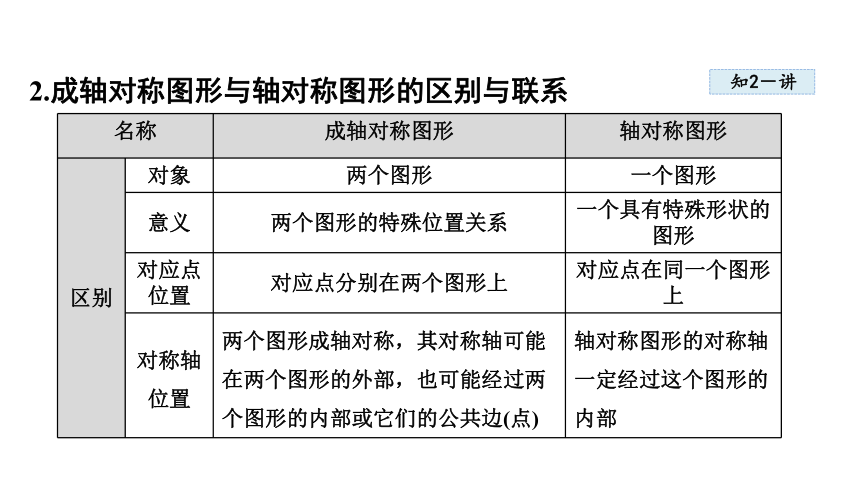
2.成轴对称图形与轴对称图形的区别与联系
名称 成轴对称图形 轴对称图形
区别 对象 两个图形 一个图形
意义 两个图形的特殊位置关系 一个具有特殊形状的图形
对应点 位置 对应点分别在两个图形上 对应点在同一个图形上
对称轴 位置 两个图形成轴对称,其对称轴可能在两个图形的外部,也可能经过两个图形的内部或它们的公共边(点) 轴对称图形的对称轴一定经过这个图形的内部
感悟新知
知2-讲
名称 成轴对称图形 轴对称图形
区别 对称轴 数量 一般只有一条 有一条或多条或无数条
联系 (1)定义中都有一条直线,都要沿着这条直线对折, (2)把成轴对称的两个图形看成一个整体,它就是一个轴对称图形. 把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条对称轴成轴对称 续表
知2-讲
感悟新知
特别解读
1. 轴对称的三个条件:
(1)有两个图形;
(2)存在一条直线;
(3)一个图形沿着这条直线折叠后与另一个图形完全重合.
2.轴对称的两个特性:
(1)成轴对称的两个图形全等,但全等的两个图形不一定成轴对称.
(2)轴对称是图形的一种全等变换.
感悟新知
知2-练
如图 16.1-1 的四组图形中,成轴对称的有( )
A. 4 组 B. 3 组 C. 2 组 D. 1 组
例2
考向:利用成轴对称图形的定义识别轴对称
知2-练
感悟新知
解题秘方:根据轴对称的定义进行解答 .
解:根据成轴对称图形的定义,可以判断只有④中的两个图形沿着某一条直线对折后能够完全重合,所以成轴对称的只有1 组.
答案:D
知2-练
感悟新知
2-1. 小明从镜子里看到镜子对面电子钟的像如图所示,则实际时间是( )
A.21: 10 B.10: 21
C.10: 51 D.12: 01
C
变式训练
感悟新知
知3-讲
知识点
成轴对称图形和轴对称图形的性质
3
1. 成轴对称图形的性质
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等图形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
特别解读:成轴对称的两个图形的对应线段所在直线平行或者重合或者相交于对称轴上某一点.
感悟新知
知3-讲
2. 线段的垂直平分线
垂直且平分一条线段的直线,叫作这条线段的垂直平分线.
线段是轴对称图形,线段的垂直平分线是它的对称轴.
3. 轴对称图形的性质
轴对称图形被对称轴分成的两部分全等 .
知3-讲
感悟新知
特别解读
被对称轴分成两部分
将两个图形看成一个整体
轴对称图形
成轴对称
知3-讲
感悟新知
特别解读
(1) 线段的垂直平分线必须满足两个条件:
①经过线段的中点;
②垂直于这条线段.两者缺一不可.
(2) 线段的垂直平分线是一条直线.
知3-讲
考向:利用轴对称图形和成轴对称图形的性质解轴对称问题
题型1 轴对称图形的性质
感悟新知
知3-练
感悟新知
如图 16.1-2 是轴对称图形,直线l 是它的对称轴.请据此解决下列问题.
(1)∠ 3 和∠ 4 有什么关系? AB 与 A′B′ 呢?
为什么?
(2)线段 DD′ 与直线 l 有什么关系?为什么?
(3)写出图中其他相等关系.(不少于三对)
例3
知3-练
感悟新知
解题秘方:紧扣轴对称图形的性质进行说明 .
解: ∠ 3= ∠ 4, AB=A′B′.
理由:因为轴对称图形被对称轴分成的两部分全等,所以它们的对应角相等,对应线段相等.
(1)∠ 3 和∠ 4 有什么关系? AB 与 A′B′ 呢?为什么?
知3-练
感悟新知
解:直线l垂直平分线段DD′.
理由:因为在轴对称图形中,对应点所连的线段被对称轴垂直平分,所以直线l垂直平分线段DD′.
AD=A′D′, ∠ 1 = ∠ 2, DC=D′C′.(答案不唯一)
(2)线段 DD′ 与直线 l 有什么关系?为什么?
(3)写出图中其他相等关系.(不少于三对)
知3-练
感悟新知
3-1. 如 图,一种滑翔伞的形状是左右成轴对称的四边 形 ABCD,其中 ∠ BAD=150 °,∠ B=40 °,则 ∠ ACD的度数是________ .
65°
变式训练
知3-练
感悟新知
如图16.1-3,∠ A=30°,∠ C′=60°,△ ABC 与
△ A′B′C′ 关于直 线 l 对 称,则∠ B=______ .
例4
题型2 成轴对称图形的性质在计算中的应用
90 °
知3-练
感悟新知
解题秘方:紧扣成轴对称图形的性质确定对应元素进行计算.
解: ∵△ ABC 与△ A′B′C′ 关于直线 l 对称,∠ C′= 60 °,
∴∠ C= ∠ C′= 60 ° .
∴ 在△ ABC 中, ∠ B=180 °-∠ A- ∠ C=90 ° .
答案:90 °
知3-练
感悟新知
4-1. 如图,在△ ABC中,∠ BAC =90 °, ∠ B=50 °,AD ⊥ BC,垂足为D,△ ADB 与△ ADB′ 关于直线AD 对称,点B 的对称点是点B′,求∠ CAB′ 的度数.
变式训练
知3-练
感悟新知
解:∵∠B=50°,∠BAC=90°,
∴∠C=90°-50°=40°.
∵AD⊥BC,△ADB与△ADB′关于直线AD对称,
∴∠AB′D=∠B=50°.
∵∠AB′D=∠C+∠CAB′,
∴∠CAB′=50°-40°=10°.
感悟新知
知4-讲
知识点
画与一个图形成轴对称的图形
4
根据成轴对称图形的性质可以画出与已知图形关于某条直线对称的图形.
画图 步骤 (1)找:在原图形上找关键点(如线段的端点、角的顶点等)
(2)画:画出各个关键点关于对称轴的对称点
(3)连:依次连接各对称点
知4-讲
感悟新知
特别解读
成轴对称图形的性质是解决轴对称问题及进行轴对称作图的依据.
感悟新知
知4-练
[母题 教材 P123 习题 T2 ]已知△ ABC 如图 16.1-4 所示,画出△ ABC 关于直线 l 对称的图形 .
例5
考向:利用轴对称的性质作图
知4-练
感悟新知
解题秘方:关于轴对称的作图问题,主要是作出关键点的对称点. 在这个问题中,点A,B,C是三个关键点,点A关于直线l的对称点就是其本身,再找到B,C两点关于直线l的对称点即可.
知4-练
感悟新知
解:如图 16.1-5.
(1)分别过点 C 和点 B 画直线 l 的垂线
段 CP 和 BQ,垂足分别为 P 和 Q;
(2)分别延长 CP 到点 C′, BQ 到点 B′,
使 C′P=CP, B′Q=BQ;
(3)依次连接 AB′, B′C′, C′A,则△ AB′C′ 就是所要画的图形 .
知4-练
感悟新知
5-1. 在方格纸中, 每个小正方形的顶点为格点, 以格点为顶点的三角形称为格点三角形. 如图是一个格点三角形. 请在图① 和图② 中各画出一个与△ ABC 成轴对称的格点三角形,并画出对称轴.
变式训练
知4-练
感悟新知
解:如图,图①中△A1B1C1,图②中△A2B2C2即为所求,其对称轴分别为直线l1,直线l2. (答案不唯一)
轴对称
轴对称图形
性质
对称轴
轴对称
16.1 轴对称
第十六章 轴对称和中心对称
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
轴对称图形
轴对称
成轴对称图形和轴对称图形的性质
画与一个图形成轴对称的图形
知1-讲
感悟新知
知识点
轴对称图形
1
1. 定义
一般地,如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴 .
感悟新知
知1-讲
特别解读
轴对称图形的三个条件:
(1)一个整体图形;
(2)一条直线——对称轴;
(3)直线两旁的部分沿直线对折后完全重合.
感悟新知
2. 几种常见的轴对称图形及其对称轴
知1-讲
名称 图形 对称轴 对称轴数量
线段 线段本身所在的直线和过线段中点的垂线 2 条
角 角平分线所在的直线 1 条
等腰三角形 底边上的高所在的直线 1 条
等边三角形 各条边上的高所在的直线 3 条
感悟新知
知1-讲
名称 图形 对称轴 对称轴数量
长方形 经过两条对边中点的直线 2 条
正方形 (1)经过两条对边中点的直线,(2)对角线所在的直线 4 条
圆 经过圆心的任意一条直线 无数条
正 n 边形 n 为奇数:过顶点与对边中点的直线;n 为偶数:过两条对边中点的直线和过相对顶点的直线 n 条
感悟新知
知1-讲
温馨提示
1. 轴对称图形是一个具有自身特性的图形,它被对称轴分成的两部分沿对称轴对折后能够互相重合,关于对称轴对称的点在同一图形上.
2. 对称轴是一条直线,而不是射线或线段.
3. 一个轴对称图形的对称轴可能有1 条,也可能有多条,还可能有无数条.
知1-练
感悟新知
人们常说:“地下文明看陕西,地上文明看山西.”山西素有“三晋古建甲天下”之称,下面是山西一些古城的图标设计图,其中不是轴对称图形的是( )
例1
考向:利用轴对称图形的定义识别轴对称图形
知1-练
感悟新知
解:A,B,D选项中的图标可以找到一条直线,使图标沿这条直线对折后直线两旁的部分能够完全重合,是轴对称图形,C 选项的图标不是轴对称图形.
解题秘方:根据轴对称图形的定义识别 .
答案:C
知1-练
感悟新知
1-1. [ 期末·承德 ] 下面四幅图分别代表二十四节气中的“立春”“芒种”“白露”“大雪”,其中是轴对称图形的是( )
D
变式训练
感悟新知
知2-讲
知识点
轴对称
2
1. 定义
一般地,如果两个图形沿某条直线对折后能够完全重合,那么我们就称这两个图形成轴对称,这条直线叫作对称轴. 关于对称轴对称的点、对称的线段、对称的角分别叫作对应点、对应线段、对应角.
感悟新知
知2-讲
2.成轴对称图形与轴对称图形的区别与联系
名称 成轴对称图形 轴对称图形
区别 对象 两个图形 一个图形
意义 两个图形的特殊位置关系 一个具有特殊形状的图形
对应点 位置 对应点分别在两个图形上 对应点在同一个图形上
对称轴 位置 两个图形成轴对称,其对称轴可能在两个图形的外部,也可能经过两个图形的内部或它们的公共边(点) 轴对称图形的对称轴一定经过这个图形的内部
感悟新知
知2-讲
名称 成轴对称图形 轴对称图形
区别 对称轴 数量 一般只有一条 有一条或多条或无数条
联系 (1)定义中都有一条直线,都要沿着这条直线对折, (2)把成轴对称的两个图形看成一个整体,它就是一个轴对称图形. 把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条对称轴成轴对称 续表
知2-讲
感悟新知
特别解读
1. 轴对称的三个条件:
(1)有两个图形;
(2)存在一条直线;
(3)一个图形沿着这条直线折叠后与另一个图形完全重合.
2.轴对称的两个特性:
(1)成轴对称的两个图形全等,但全等的两个图形不一定成轴对称.
(2)轴对称是图形的一种全等变换.
感悟新知
知2-练
如图 16.1-1 的四组图形中,成轴对称的有( )
A. 4 组 B. 3 组 C. 2 组 D. 1 组
例2
考向:利用成轴对称图形的定义识别轴对称
知2-练
感悟新知
解题秘方:根据轴对称的定义进行解答 .
解:根据成轴对称图形的定义,可以判断只有④中的两个图形沿着某一条直线对折后能够完全重合,所以成轴对称的只有1 组.
答案:D
知2-练
感悟新知
2-1. 小明从镜子里看到镜子对面电子钟的像如图所示,则实际时间是( )
A.21: 10 B.10: 21
C.10: 51 D.12: 01
C
变式训练
感悟新知
知3-讲
知识点
成轴对称图形和轴对称图形的性质
3
1. 成轴对称图形的性质
如果两个图形关于某一条直线成轴对称,那么,这两个图形是全等图形,它们的对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分.
特别解读:成轴对称的两个图形的对应线段所在直线平行或者重合或者相交于对称轴上某一点.
感悟新知
知3-讲
2. 线段的垂直平分线
垂直且平分一条线段的直线,叫作这条线段的垂直平分线.
线段是轴对称图形,线段的垂直平分线是它的对称轴.
3. 轴对称图形的性质
轴对称图形被对称轴分成的两部分全等 .
知3-讲
感悟新知
特别解读
被对称轴分成两部分
将两个图形看成一个整体
轴对称图形
成轴对称
知3-讲
感悟新知
特别解读
(1) 线段的垂直平分线必须满足两个条件:
①经过线段的中点;
②垂直于这条线段.两者缺一不可.
(2) 线段的垂直平分线是一条直线.
知3-讲
考向:利用轴对称图形和成轴对称图形的性质解轴对称问题
题型1 轴对称图形的性质
感悟新知
知3-练
感悟新知
如图 16.1-2 是轴对称图形,直线l 是它的对称轴.请据此解决下列问题.
(1)∠ 3 和∠ 4 有什么关系? AB 与 A′B′ 呢?
为什么?
(2)线段 DD′ 与直线 l 有什么关系?为什么?
(3)写出图中其他相等关系.(不少于三对)
例3
知3-练
感悟新知
解题秘方:紧扣轴对称图形的性质进行说明 .
解: ∠ 3= ∠ 4, AB=A′B′.
理由:因为轴对称图形被对称轴分成的两部分全等,所以它们的对应角相等,对应线段相等.
(1)∠ 3 和∠ 4 有什么关系? AB 与 A′B′ 呢?为什么?
知3-练
感悟新知
解:直线l垂直平分线段DD′.
理由:因为在轴对称图形中,对应点所连的线段被对称轴垂直平分,所以直线l垂直平分线段DD′.
AD=A′D′, ∠ 1 = ∠ 2, DC=D′C′.(答案不唯一)
(2)线段 DD′ 与直线 l 有什么关系?为什么?
(3)写出图中其他相等关系.(不少于三对)
知3-练
感悟新知
3-1. 如 图,一种滑翔伞的形状是左右成轴对称的四边 形 ABCD,其中 ∠ BAD=150 °,∠ B=40 °,则 ∠ ACD的度数是________ .
65°
变式训练
知3-练
感悟新知
如图16.1-3,∠ A=30°,∠ C′=60°,△ ABC 与
△ A′B′C′ 关于直 线 l 对 称,则∠ B=______ .
例4
题型2 成轴对称图形的性质在计算中的应用
90 °
知3-练
感悟新知
解题秘方:紧扣成轴对称图形的性质确定对应元素进行计算.
解: ∵△ ABC 与△ A′B′C′ 关于直线 l 对称,∠ C′= 60 °,
∴∠ C= ∠ C′= 60 ° .
∴ 在△ ABC 中, ∠ B=180 °-∠ A- ∠ C=90 ° .
答案:90 °
知3-练
感悟新知
4-1. 如图,在△ ABC中,∠ BAC =90 °, ∠ B=50 °,AD ⊥ BC,垂足为D,△ ADB 与△ ADB′ 关于直线AD 对称,点B 的对称点是点B′,求∠ CAB′ 的度数.
变式训练
知3-练
感悟新知
解:∵∠B=50°,∠BAC=90°,
∴∠C=90°-50°=40°.
∵AD⊥BC,△ADB与△ADB′关于直线AD对称,
∴∠AB′D=∠B=50°.
∵∠AB′D=∠C+∠CAB′,
∴∠CAB′=50°-40°=10°.
感悟新知
知4-讲
知识点
画与一个图形成轴对称的图形
4
根据成轴对称图形的性质可以画出与已知图形关于某条直线对称的图形.
画图 步骤 (1)找:在原图形上找关键点(如线段的端点、角的顶点等)
(2)画:画出各个关键点关于对称轴的对称点
(3)连:依次连接各对称点
知4-讲
感悟新知
特别解读
成轴对称图形的性质是解决轴对称问题及进行轴对称作图的依据.
感悟新知
知4-练
[母题 教材 P123 习题 T2 ]已知△ ABC 如图 16.1-4 所示,画出△ ABC 关于直线 l 对称的图形 .
例5
考向:利用轴对称的性质作图
知4-练
感悟新知
解题秘方:关于轴对称的作图问题,主要是作出关键点的对称点. 在这个问题中,点A,B,C是三个关键点,点A关于直线l的对称点就是其本身,再找到B,C两点关于直线l的对称点即可.
知4-练
感悟新知
解:如图 16.1-5.
(1)分别过点 C 和点 B 画直线 l 的垂线
段 CP 和 BQ,垂足分别为 P 和 Q;
(2)分别延长 CP 到点 C′, BQ 到点 B′,
使 C′P=CP, B′Q=BQ;
(3)依次连接 AB′, B′C′, C′A,则△ AB′C′ 就是所要画的图形 .
知4-练
感悟新知
5-1. 在方格纸中, 每个小正方形的顶点为格点, 以格点为顶点的三角形称为格点三角形. 如图是一个格点三角形. 请在图① 和图② 中各画出一个与△ ABC 成轴对称的格点三角形,并画出对称轴.
变式训练
知4-练
感悟新知
解:如图,图①中△A1B1C1,图②中△A2B2C2即为所求,其对称轴分别为直线l1,直线l2. (答案不唯一)
轴对称
轴对称图形
性质
对称轴
轴对称
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
