【期末专项培优】解决问题的策略(含解析)-2024-2025学年五年级下册数学苏教版
文档属性
| 名称 | 【期末专项培优】解决问题的策略(含解析)-2024-2025学年五年级下册数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 15:34:27 | ||
图片预览



文档简介
期末专项培优 解决问题的策略
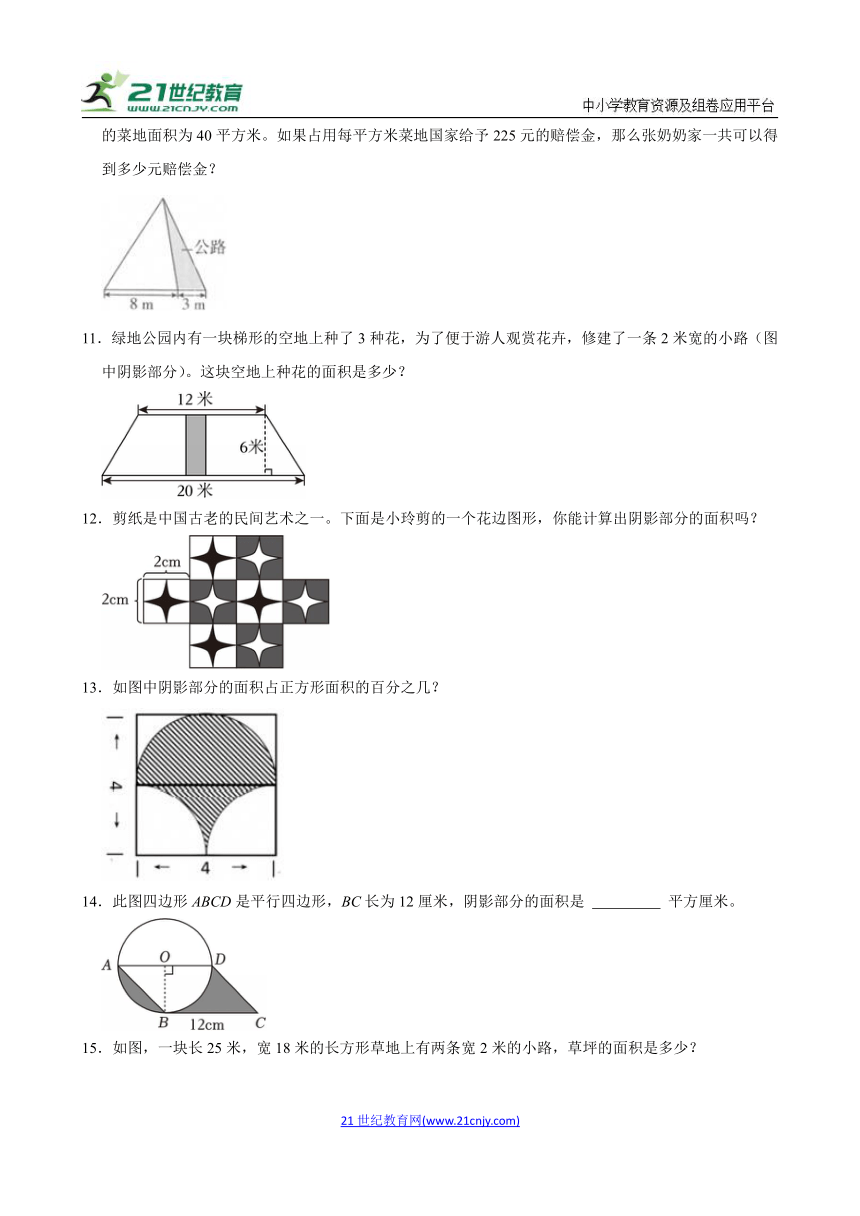
1.李伯伯家有如图所示的两块菜地,其中一块平行四边形地种青菜,另一块三角形地种萝卜。这两块地的总面积是多少平方米?
2.如图,这是一枚“外圆内方”的古钱币,该钱币外圆的周长为9.42厘米,中间正方形孔的边长为1厘米,如果把这枚钱币放在桌面上,它所覆盖的面积是多少平方厘米?(π值取3.14)
3.某开发区大标语牌上要画出如图所示的三种标点符号:句号、逗号、问号。已知大圆半径相同,都为R;小圆半径也相同,都为r;而且R:r=2:1.如果都是均匀用料,画哪个标点符号的油漆用得最多?
4.24小时开放的“河东驿站”,为广大市民提供了取暖纳凉、歇脚喝水等便利服务,被誉为深夜依旧为您亮灯的“家”。如图是某驿站的平面图,请你用喜欢的方法算一算这个驿站的占地面积是多少?
5.如图,长方形ABCD的长是12米,宽是6米,E、F分别是长方形CD边和AD边上的中点,涂色部分的面积是多少平方米?
6.某小区一块长方形的绿地的造型如图所示(单位:m),其中两个扇形表示绿地,两块绿地用五彩石隔开,那么需铺多大面积的五彩石?(保留π)
7.刘叔叔新买了一套住房,平面图如图。
(单位:米)他在装修时遇到了一些问题:
(1)这套房子一共有多少平方米?
(2)如果用复合地板铺“南卧室”,每平方米售价60元,一共需要多少元?
8.一块平行四边形的草坪中有一块宽0.6米,长15米的水渠(如图),这块草坪的面积是多少平方米?
9.两个长12cm、宽8cm的长方形(如图)摆放后,组合图形的面积是多少?
10.张奶奶家原有一块三角形菜地(如图中最大的三角形),由于公路拓宽,菜地被占用了一部分,剩下的菜地面积为40平方米。如果占用每平方米菜地国家给予225元的赔偿金,那么张奶奶家一共可以得到多少元赔偿金?
11.绿地公园内有一块梯形的空地上种了3种花,为了便于游人观赏花卉,修建了一条2米宽的小路(图中阴影部分)。这块空地上种花的面积是多少?
12.剪纸是中国古老的民间艺术之一。下面是小玲剪的一个花边图形,你能计算出阴影部分的面积吗?
13.如图中阴影部分的面积占正方形面积的百分之几?
14.此图四边形ABCD是平行四边形,BC长为12厘米,阴影部分的面积是 平方厘米。
15.如图,一块长25米,宽18米的长方形草地上有两条宽2米的小路,草坪的面积是多少?
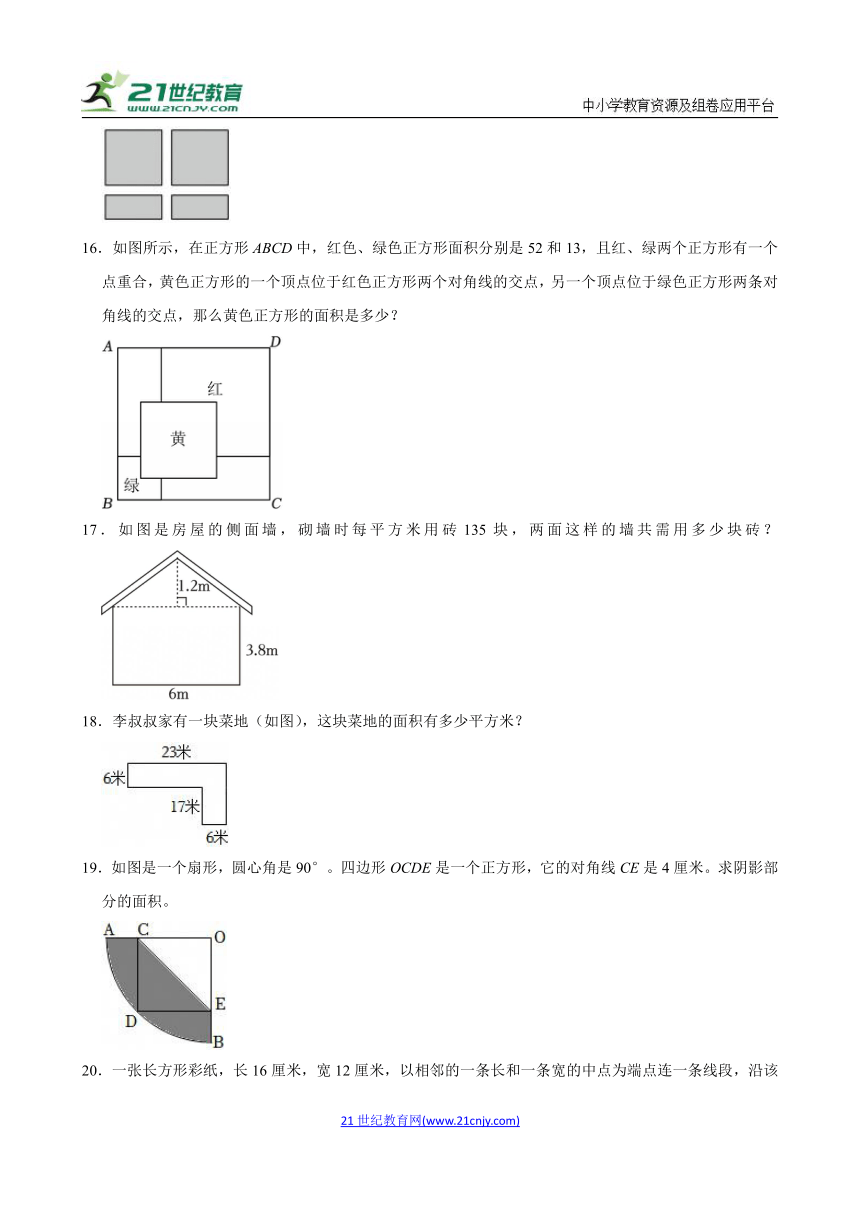
16.如图所示,在正方形ABCD中,红色、绿色正方形面积分别是52和13,且红、绿两个正方形有一个点重合,黄色正方形的一个顶点位于红色正方形两个对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,那么黄色正方形的面积是多少?
17.如图是房屋的侧面墙,砌墙时每平方米用砖135块,两面这样的墙共需用多少块砖?
18.李叔叔家有一块菜地(如图),这块菜地的面积有多少平方米?
19.如图是一个扇形,圆心角是90°。四边形OCDE是一个正方形,它的对角线CE是4厘米。求阴影部分的面积。
20.一张长方形彩纸,长16厘米,宽12厘米,以相邻的一条长和一条宽的中点为端点连一条线段,沿该线段剪去一个角(如图),剩下的面积是多少平方厘米?
21.如图,王叔叔用9.42米长的篱笆靠墙围了一个最大的养鸡场,这个养鸡场的面积是多少平方米?如果每只鸡占地0.2平方米,这个养鸡场最多可以养多少只鸡?(根据实际情况,结果保留整数)
22.一块长方形空地因建房子被占掉一部分,剩下部分的面积(如图阴影所示)是多少平方米?
23.中国建筑中经常见到“外方内圆”和“外圆内方”的设计。如图中两个圆的直径都是4厘米,分别计算正方形和圆之间的部分各是多少平方厘米?
24.在小区空地上修一条长方形和一条平行四边形的小路,再在涂色部分种上花草,种花草的面积是多少平方米?合多少公顷?
25.如图,大正方形的边长是14厘米,小正方形的边长是10厘米。求阴影部分的面积。
26.学校有一块劳动基地,现将它划分成三部分分别用来种玉米、红薯、棉花,如图。
(1)种玉米的面积是多少平方米?
(2)如果每平方米种3棵棉花,一共能种多少棵棉花?
27.公园要进行绿化,在一个花坛(如图)中种绿植(涂色部分)。已知每平方米绿植需要12元,则给这个花坛种绿植需要花费多少钱?
28.一块草坪被4条1米宽的小路平均分成了9小块,草坪的面积是多少平方米?
29.如图,一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
30.校园内有一个梯形花圃,这个梯形上底长27米,下底长38米,高24米。其中有一块三角形的地方种植郁金香(如图阴影部分),其他地方种植了月季花。月季花的种植面积是多少平方米?
31.某实验小学有一块劳动实践基地(如图)。这块地的面积是多少平方米?
32.如图是一个长28米、宽22米的花坛,在这个花坛的四周要修宽3米的小路。小路的面积是多少平方米?
33.如图所示,正方形ABCD边长为10,正方形BEFG边长为6,正方形JIHC面积未知,则阴影部分的面积是多少?
34.用两块长方形纸片和一块正方形纸片拼成一个大正方形(如图),长方形纸片面积分别是44平方厘米和28平方厘米,原来正方形面积是多少平方厘米?
35.将一个边长为10厘米的正方形纸对折后剪去一个上底是2.5厘米,下底是5厘米,高是2厘米的梯形,然后打开(如图所示),求剩下部分的面积.
36.李叔叔要粉刷一面墙(如图),如果粉刷1平方米墙需用涂料800g,那么粉刷这面墙一共需要多少千克的涂料?
37.如图是同一块草地的占地平面图。(单位:m)
(1)要算它的占地面积,你有几种割补方法?请在图中画出相应的虚线。(备用图若不够,可画草图来补充)
(2)它的占地面积有多大?(选一种来计算,先说明选的是图几)
38.如图,长方形ABCD中,线段AB长8cm,线段BC长15cm.四边形EFGH的面积是9cm2,涂色部分的面积是多少?
39.两张边长都为6cm的正方形纸片,分别按如图剪下不同规格的圆片.哪张纸片剩下的废料(阴影部分)多?
40.“月季花展”是人民公园的特色之一,如图是人民公园的地图,为了估算人民公园的面积,田田勾画出下面的图形(如左图),并用地图的测距工具测出所需的数据(如右图)。请你帮助田田算一算人民公园的面积。
(1)你想怎样求这个图形的面积?在如右图中画一画。
(2)按照你的想法算出人民公园的面积是多少平方米?
41.潍坊萝卜,又称潍县萝卜,素有“烟台苹果、莱阳梨、不如潍县萝卜皮”之说,深受人们的喜爱。
张伯伯承包了一块不规则的萝卜地,萝卜地形状如图所示,张伯伯想把这块地分成两块,一块是梯形,种水果青萝卜;一块是三角形,种冰糖心萝卜。请你帮张伯伯在图中分一分,算一算,每块萝卜地的面积是多少公顷?
42.如图:一个长方形铁皮,剪下一个正方形后,剩余的面积是61平方厘米,剪下的正方形的面积是多少?
43.市民广场中一个正方形花坛的四周有一条2米宽的石子路,石子路的总面积是48平方米,中间花坛的面积是多少平方米?
44.下面是一批小麦地的平面图。如果每平方米收小麦1.5千克。这块地可收小麦多少千克?
45.在一块平行四边形空地上种植一些草皮,空地中间留有一条2米宽的小路,
上面铺设了彩砖供人行走。(如图)
(1)需要种植草皮的面积有多大?
(2)如果每平方米草皮需要13元,每平方米彩砖需要24元,那么铺完这块空地共需要多少元?
46.如图,一块长方形草地,长方形的长是16米,宽是10米,中间铺了一条2米宽的石子路。那么草地部分面积有多大?
47.学校学农基地有一块菜地(如图所示),这块菜地有多少平方米?如果每平方米菜地产生25元收益,这块菜地一共可以产生收益多少元?
48.近年来我国新能源汽车发展迅速。某市开发区新建一处新能源汽车销售中心(如图所示)。这个销售中心的占地面积是多少平方米?(用两种方法解答)
49.市政府准备在街心花园建一个花圃(见图).这个花圃需要占地多少平方米?
50.一块近似平行四边形的草坪,中间有一条石子路(如图)。如果铺1平方米草坪需要7.5元,铺这块草坪大约需要多少钱?
51.已知甲的面积比乙的面积大57平方厘米,半圆的直径是20厘米,求BC的长.
52.如图,单位厘米,求图中阴影部分的周长是多少厘米?
53.小强有一个平行四边形玩具(如图),已知阴影部分三角形的面积是6平方分米,空白部分(梯形)小强用来摆拼图,摆拼图部分的面积是多少平方分米?
54.如图,一块平行四边形的草地中间有一条长8米,宽1米的长方形小路。草地种草部分的面积是多少平方米?
55.如图,长方形ABCD的长是16厘米,宽是12厘米,BE=15厘米,CF和BE垂直,那么CF的长是多少厘米?
56.比一比,谁的面积大?
57.一个站台的横截面如图,已知梯形的上底是2.1米,下底是3.4米,涂色阴影部分面积为4.76平方米,求梯形的面积是多少平方米?如果按这个面积涂颜料,每平方米需要涂料1.5千克,求剩下的部分还需要多少千克涂料?
58.如图所示,学校在一块长方形的空地上围了一个直径是8米的半圆形花坛,把剩余地方(阴影部分)铺成了草坪。花坛的面积和草坪的周长分别是多少?
59.一块近似长方形的平地,中间有一块近似三角形草地,现在三角形草地之外其余部分种上竹子,如果每平方米竹子造价30元,这块竹林大约需要多少钱?
60.如图是一张长方形卡纸和一张三角形卡纸部分重叠在一起后得到的图形。已知长方形卡纸的面积比三角形卡纸的面积小16平方厘米,你能算出线段CE的长度吗?(单位:厘米)
期末专项培优 解决问题的策略
参考答案与试题解析
1.李伯伯家有如图所示的两块菜地,其中一块平行四边形地种青菜,另一块三角形地种萝卜。这两块地的总面积是多少平方米?
【答案】100平方米。
【分析】通过观察图形可知,这两个底拼成一个梯形,梯形的上底是(9.3+6.4)米,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(9.3+6.4+9.3)×8÷2
=25×8÷2
=200÷2
=100(平方米)
答:这两个地的总面积是100平方米。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
2.如图,这是一枚“外圆内方”的古钱币,该钱币外圆的周长为9.42厘米,中间正方形孔的边长为1厘米,如果把这枚钱币放在桌面上,它所覆盖的面积是多少平方厘米?(π值取3.14)
【答案】6.065平方厘米。
【分析】通过观察图形可知,阴影部分的面积等于圆的面积减去正方形的面积,根据圆的面积公式:S=πr2,正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:3.14×(9.42÷3.14÷2)2﹣1×1
=3.14×2.25﹣1
=7.065﹣1
=6.065(平方厘米)
答:它所覆盖的面积是6.065平方厘米。
【点评】此题主要考查圆的面积公式、正方形的面积公式的灵活运用,关键是熟记公式。
3.某开发区大标语牌上要画出如图所示的三种标点符号:句号、逗号、问号。已知大圆半径相同,都为R;小圆半径也相同,都为r;而且R:r=2:1.如果都是均匀用料,画哪个标点符号的油漆用得最多?
【答案】问号。
【分析】根据环形面积公式:S=π(R2﹣r2),把数据代入公式求出句号的面积;逗号的面积通过旋转转化为大半圆的面积,问号的面积等于环形的面积加上小圆的面积,根据圆的公式:S=πr2,把数据代入公式求出它们的面积,然后进行比较即可。
【解答】解:设r为1,则R为2,
句号的面积:
π×(22﹣12)
=π×(4﹣1)
=π×3
=3π
逗号的面积:
π×22÷2
=π×4÷2
=2π
问号的面积:
π×(22﹣12)π×12
=π×(4﹣1)π×1
π+π
π
π>3π>2π
答:问号的油漆用量最多。
【点评】解答求组合图形的面积,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答。
4.24小时开放的“河东驿站”,为广大市民提供了取暖纳凉、歇脚喝水等便利服务,被誉为深夜依旧为您亮灯的“家”。如图是某驿站的平面图,请你用喜欢的方法算一算这个驿站的占地面积是多少?
【答案】97平方米。
【分析】根据图形的特点,可以分成一个正方形和一个长方形,根据正方形的面积公式:S=a2,长方形的面积公式:S=ab,把数据代入公式求出它们的面积和即可。
【解答】解:如图:
(11﹣4)×7+12×4
=7×7+48
=49+48
=97(平方米)
答:这个驿站的占地面积是97平方米。
【点评】此题主要考查正方形、长方形面积公式的灵活运用,关键是熟记公式。
5.如图,长方形ABCD的长是12米,宽是6米,E、F分别是长方形CD边和AD边上的中点,涂色部分的面积是多少平方米?
【答案】36平方米。
【分析】连接BD,E、F分别是长方形CD边和AD边上的中点,则三角形BDE面积=三角形BCE的面积,三角形BDF的面积=三角形ABF的面积,所以涂色部分的面积等于长方形面积的一半,据此解答即可。
【解答】解:如图:
连接BD,E、F分别是长方形CD边和AD边上的中点,则三角形BDE面积=三角形BCE的面积,三角形BDF的面积=三角形ABF的面积,所以涂色部分的面积等于长方形面积的一半,
12×6÷2
=72÷2
=36(平方米)
答:涂色部分的面积是36平方米。
【点评】解答求不规则图形的面积,关键是通过“转化”,把不规则图形转化为规则图形进行解答。
6.某小区一块长方形的绿地的造型如图所示(单位:m),其中两个扇形表示绿地,两块绿地用五彩石隔开,那么需铺多大面积的五彩石?(保留π)
【答案】见试题解答内容
【分析】通过观察图形发现,铺五彩石的面积等于长方形的面积减去两个扇形的面积,根据长方形的面积公式:S=ab,圆的面积公式:S=πr2,把数据分别代入公式解答.
【解答】解:(a+b)×aπa2πb2
=a2+abπa2πb2(平方米)
答:需要铺(a2+abπa2πb2)平方米五彩石.
【点评】解答求组合图形的面积,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答.
7.刘叔叔新买了一套住房,平面图如图。
(单位:米)他在装修时遇到了一些问题:
(1)这套房子一共有多少平方米?
(2)如果用复合地板铺“南卧室”,每平方米售价60元,一共需要多少元?
【答案】(1)88平方米;
(2)1200元。
【分析】(1)先求出这套房子的长、宽,然后根据长方形的面积=长×宽,把数据代入公式解答。
(2)根据长方形的面积=长×宽,求出南卧室的面积,然后根据单价×数量=总价,列式解答。
【解答】解:(1)(5+1+5)×(4+4)
=11×8
=88(平方米)
答:这套房子一共有88平方米。
(2)5×4×60
=20×60
=1200(元)
答:一共需要1200元。
【点评】此题主要考查长方形面积公式的灵活应用,以及单价、数量、总价三者之间的关系及应用,关键是熟记公式。
8.一块平行四边形的草坪中有一块宽0.6米,长15米的水渠(如图),这块草坪的面积是多少平方米?
【答案】666平方米。
【分析】整块草坪是个平行四边形,水渠是个长方形,且长方形的长是平行四边形的高,草坪面积=平行四边形﹣长方形面积,平行四边形面积=底×高,长方形面积=长×宽,据此列式解答。
【解答】解:45×15﹣15×0.6
=675﹣9
=666(平方米)
答:这块草坪的面积是666平方米。
【点评】此题主要考查平行四边形的面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
9.两个长12cm、宽8cm的长方形(如图)摆放后,组合图形的面积是多少?
【答案】128平方厘米。
【分析】根据组合图形的面积=大长方形的面积+一个小长方形的面积,据此求解即可。
【解答】解:12×8+(12﹣8)×8
=96+4×8
=96+32
=128(平方厘米)
答:组合图形的面积是128平方厘米。
【点评】本题主要考查了组合图形,解题的关键是求出小长方形的长与宽。
10.张奶奶家原有一块三角形菜地(如图中最大的三角形),由于公路拓宽,菜地被占用了一部分,剩下的菜地面积为40平方米。如果占用每平方米菜地国家给予225元的赔偿金,那么张奶奶家一共可以得到多少元赔偿金?
【答案】3375元。
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,据此求出高,把数据代入公式求出被占用的面积,然后再乘每平方米的赔偿金即可。
【解答】解:40×2÷8
=80÷8
=10(米)
3×10÷2×225
=15×225
=3375(元)
答:张奶奶家一共可以得到3375元赔偿金。
【点评】此题主要考查三角形面积公式的灵活运用,关键是熟记公式。
11.绿地公园内有一块梯形的空地上种了3种花,为了便于游人观赏花卉,修建了一条2米宽的小路(图中阴影部分)。这块空地上种花的面积是多少?
【答案】84平方米。
【分析】观察图形可知,这块空地上种花的面积=梯形的面积﹣长方形的面积,根据梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,代入数据计算即可求解。
【解答】解:(12+20)×6÷2﹣6×2
=32×6÷2﹣12
=96﹣12
=84(平方米)
答:这块空地上种花的面积是84平方米。
【点评】此题主要考查梯形、长方形面积公式的灵活运用,关键是熟记公式。
12.剪纸是中国古老的民间艺术之一。下面是小玲剪的一个花边图形,你能计算出阴影部分的面积吗?
【答案】16平方厘米。
【分析】通过观察图形可知,阴影部分的面积可以通过平移“转化”为边长是2厘米的4个正方形的面积。根据正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:2×2×4
=4×4
=16(平方厘米)
答:阴影部分的面积是16平方厘米。
【点评】此题解答的关键是通过“转化”把阴影部分的面积转化为4个正方形的面积,根据正方形的面积公式解答。
13.如图中阴影部分的面积占正方形面积的百分之几?
【答案】50%。
【分析】通过观察可知,图中正方形被平均分成两份,两个圆正好等于一个半圆,所以阴影部分的面积占正方形面积的一半;据此解答即可。
【解答】解:1÷2=50%
答:阴影部分的面积占正方形面积的50%。
【点评】解答本题的关键是理解两个圆正好等于一个半圆。
14.此图四边形ABCD是平行四边形,BC长为12厘米,阴影部分的面积是 36 平方厘米。
【答案】36。
【分析】把左边的阴影部分旋转到右边,可得:阴影部分的面积=平行四边形的一半,据此求解即可。
【解答】解:如图:
12×(12÷2)÷2
=12×6÷2
=36(平方厘米)
答:阴影部分的面积是36平方厘米。
故答案为:36。
【点评】本题主要考查了组合图形的面积,解题的关键是把不规则图形的面积转化为规则图形的面积。
15.如图,一块长25米,宽18米的长方形草地上有两条宽2米的小路,草坪的面积是多少?
【答案】368平方米。
【分析】根据图形的特点,可以通过平移把小路两边的草坪合并为长(25﹣2)米,宽(18﹣2)米的长方形,根据长方形的面积=长×宽,把数据代入公式解答。
【解答】解:(25﹣2)×(18﹣2)
=23×16
=368(平方米)
答:草坪的面积是368平方米。
【点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
16.如图所示,在正方形ABCD中,红色、绿色正方形面积分别是52和13,且红、绿两个正方形有一个点重合,黄色正方形的一个顶点位于红色正方形两个对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,那么黄色正方形的面积是多少?
【答案】见试题解答内容
【分析】如图:因为黄色正方形的两个顶点均位于两个正方形两条对角线的交点,所以②的面积是:52÷4=13,④的面积是:13÷4=3.25,所以④的面积:②的面积=3.25:13=1:4=1:22,由于边长的平方比等于面积比,则①的面积:④的面积=②的面积:③的面积=1:2,所以①的面积=③的面积=3.25×2=6.5,然后把①②③④的面积相加即可求出黄色正方形的面积.据此解答.
【解答】解:如图:根据分析得:
②的面积是:52÷4=13,
④的面积是:13÷4=3.25,
所以④的面积:②的面积=3.25:13=1:4=1:22,
由于边长的平方比等于面积比,则①的面积:④的面积=②的面积:③的面积=2:1,
所以①的面积=③的面积=3.25×2=6.5,
黄色正方形的面积是:6.5+13+6.5+3.25=29.25.
答:黄色正方形的面积是29.25.
【点评】此题重点考查学生对图形的分析能力,对于此类问题,应认真分析图意,找出各图形之间的关系;本题关键是明确:边长的平方比等于面积比.
17.如图是房屋的侧面墙,砌墙时每平方米用砖135块,两面这样的墙共需用多少块砖?
【答案】7128块砖。
【分析】先依据三角形和长方形的面积公式求出这面墙的面积,再乘2即两面墙的面积,然后乘每平方米需要的砖的块数,问题即可得解。
【解答】解:(6×1.2÷2+6×3.8)×2×135
=(3.6+22.8)×2×135
=26.4×2×135
=7128(块)
答:两面这样的墙共需用7128块砖。
【点评】此题主要考查三角形和长方形的面积的计算方法在实际生活中的应用。
18.李叔叔家有一块菜地(如图),这块菜地的面积有多少平方米?
【答案】240平方米。
【分析】根据题意可知,这块菜地的面积等于两块长方形菜地的面积的和,一块长方形菜地的长为23米,宽为6米;另一块长方形菜地的长为17米,宽为6米,长方形的面积=长×宽,依此计算并解答即可。
【解答】解:如图:
23×6=138(平方米)
17×6=102(平方米)
138+102=240(平方米)
答:这块菜地的面积有240平方米。
【点评】熟练掌握长方形的面积的计算是解答此题的关键。
19.如图是一个扇形,圆心角是90°。四边形OCDE是一个正方形,它的对角线CE是4厘米。求阴影部分的面积。
【答案】8.56平方厘米。
【分析】因为CE是正方形OCDE的对角线,所以OD=CE=4(厘米),即扇形所在圆的半径为4厘米,再根据阴影部分的面积=扇形的面积﹣空白三角形的面积,据此求解即可。
【解答】解:三角形COE的高是OD的一半,即CE的一半,4÷2=2(厘米)
3.14×42÷4﹣4×(4÷2)÷2
=3.14×16÷4﹣4×2÷2
=12.56﹣4
=8.56(平方厘米)
答:阴影部分的面积是8.56平方厘米。
【点评】本题主要考查了组合图形的面积,解题的关键把不规则图形转化为规则图形。
20.一张长方形彩纸,长16厘米,宽12厘米,以相邻的一条长和一条宽的中点为端点连一条线段,沿该线段剪去一个角(如图),剩下的面积是多少平方厘米?
【答案】168平方厘米。
【分析】通过观察图形可知,剩下部分的面积等于长方形的面积减去三角形的面积,根据长方形的面积公式:S=ab,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:16×12﹣(16÷2)×(12÷2)÷2
=192﹣8×6÷2
=192﹣24
=168(平方厘米)
答:剩下的面积是168平方米。
【点评】此题主要考查长方形、三角形面积公式的灵活运用,关键是熟记公式。
21.如图,王叔叔用9.42米长的篱笆靠墙围了一个最大的养鸡场,这个养鸡场的面积是多少平方米?如果每只鸡占地0.2平方米,这个养鸡场最多可以养多少只鸡?(根据实际情况,结果保留整数)
【答案】28.26平方米,141只。
【分析】通过观察图形可知,两面靠墙,用9.42米篱笆围成一个圆的养鸡场,根据圆的周长公式:C=2πr,那么r=C÷π÷2,据此可以求出半径,再根据圆的面积公式:S=πr2,求出养鸡场的面积,然后根据“包含”除法的意义,用除法解答。
【解答】解:9.42×4÷3.14÷2
=37.68÷3.14÷2
=12÷2
=6(米)
3.14×62
=3.14×36
=28.26(平方米)
28.26÷0.2≈141(只)
答:这个养鸡场的面积是28.26平方米,这个养鸡场最多可以养141只鸡。
【点评】此题主要考查圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式,重点是求出养鸡场的半径。
22.一块长方形空地因建房子被占掉一部分,剩下部分的面积(如图阴影所示)是多少平方米?
【答案】1200平方米。
【分析】根据阴影部分的面积=长方形的面积﹣三角形的面积,据此求解即可。
【解答】解:50×(12+18)﹣50×12÷2
=50×30﹣600÷2
=1500﹣300
=1200(平方米)
答:剩下部分的面积(如图阴影所示)是1200平方米。
【点评】本题主要考查了组合图形的面积,解题的关键是把不规则图形的面积转化为规则图形的面积。
23.中国建筑中经常见到“外方内圆”和“外圆内方”的设计。如图中两个圆的直径都是4厘米,分别计算正方形和圆之间的部分各是多少平方厘米?
【答案】(1)3.44平方厘米;(2)4.56平方厘米。
【分析】(1)由图示可知,圆的直径等于正方形的边长,正方形和圆之间的部分的面积等于正方形的面积减去圆的面积;
(2)根据图示,把正方形分成两个等腰直角三角形,三角形的底等于圆的直径,三角形的高等于圆的半径。正方形和圆之间的部分的面积等于圆的面积减去正方形的面积。
利用正方形面积公式:S=a2,圆的面积公式:S=πr2,三角形面积公式:S=ah÷2,计算即可。
【解答】解:(1)4×4﹣3.14×(4÷2)2
=16﹣12.56
=3.44(平方厘米)
答:正方形和圆之间的部分的面积是3.44平方厘米。
(2)3.14×(4÷2)2﹣4÷2×2×4÷2
=12.56﹣8
=4.56(平方厘米)
答:正方形和圆之间的部分的面积是4.56平方厘米。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
24.在小区空地上修一条长方形和一条平行四边形的小路,再在涂色部分种上花草,种花草的面积是多少平方米?合多少公顷?
【答案】200000平方米,2公顷。
【分析】根据图形的特点,可以通过平移把涂色的三部分拼成一个底是(40+160)米,高是100米的平行四边形的面积,根据平行四边形的面积公式:S=ah,把数据代入公式解答。
【解答】解:(40+160)×100
=200×100
=20000(平方米)
20000平方米=2公顷
答:种花草的面积是20000平方米,合2公顷。
【点评】此题主要考查平行四边形面积公式的灵活运用,关键是熟记公式,重点是通过平移把涂色部分的面积拼成一个平行四边形的面积。
25.如图,大正方形的边长是14厘米,小正方形的边长是10厘米。求阴影部分的面积。
【答案】98平方厘米。
【分析】通过观察图形可知,阴影部分的面积等于长(14+10)厘米,宽14厘米的长方形的面积减去空白部分3个三角形的面积,根据长方形的面积公式;S=ab,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:(14+10)×14﹣14×14÷2﹣(14+10)×10÷2﹣(14﹣10)×10÷2
=24×14﹣196÷2﹣24×10÷2﹣4×10÷2
=336﹣98﹣120﹣20
=98(平方厘米)
答:阴影部分的面积是98平方厘米。
【点评】解答求组合图形的面积,关键是观察分析图形是由哪几部分组成的,是各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答。
26.学校有一块劳动基地,现将它划分成三部分分别用来种玉米、红薯、棉花,如图。
(1)种玉米的面积是多少平方米?
(2)如果每平方米种3棵棉花,一共能种多少棵棉花?
【答案】(1)9平方米;
(2)99棵。
【分析】(1)根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
(2)根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式求出棉花地的面积,然后再乘每平方米种棉花的棵数即可。
【解答】解:3×6÷2
=18÷2
=9(平方米)
答:玉米地的面积是9平方米。
(2)(4+7)×6÷2×3
=11×6÷2×3
=33×3
=99(棵)
答:一共能种99棵棉花。
【点评】此题主要考查三角形、梯形面积公式的灵活运用,关键是熟记公式。
27.公园要进行绿化,在一个花坛(如图)中种绿植(涂色部分)。已知每平方米绿植需要12元,则给这个花坛种绿植需要花费多少钱?
【答案】768元。
【分析】通过观察图形可知,可以通过平移转化为一个边长是(2×4)米的正方形的面积,根据正方形的面积公式:S=a2,把数据代入公式求出花坛的面积,然后再乘每平方米的费用即可。
【解答】解:(2×4)×(2×4)×12
=8×8×12
=64×12
=768(元)
答:给这个花坛种绿植需要花费768元。
【点评】解答求不规则图形的面积,关键是通过“转化”,把不规则图形转化为规则图形进行解答。
28.一块草坪被4条1米宽的小路平均分成了9小块,草坪的面积是多少平方米?
【答案】见试题解答内容
【分析】一块草坪被4条1米宽的小路平均分成了9小块,分成的每一块草坪的长是(45﹣1×2)÷3米,宽是(27﹣1×2)÷3米,根据长方形的面积公式:S=ab求出一块的面积,再乘9即可.据此解答.
【解答】解:[(45﹣1×2)÷3]×[(27﹣1×2)÷3]×9
9
=1075(平方米)
答:草坪的实际面积是1075平方米.
【点评】本题的重点是求出每一小块草坪的长和宽,进而求出一块的面积,然后再求总面积.
29.如图,一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
【答案】2992米。
【分析】方法一:一块草坪被4条1米宽的小路平均分成了9小块,分成的每一块草坪的长是(90﹣1×2)÷3米,宽是(36﹣1×2)÷3米,根据长方形的面积公式:S=ab求出一块的面积,再乘9即可解答。
方法二:观察图形,通过平移可得草坪的面积实际上就是长为90﹣2=88(米)、宽为36﹣2=34(米)的长方形的面积,然后再根据长方形的面积公式:S=ab进行解答。
【解答】解:方法一:[(90﹣1×2)÷3]×[(36﹣1×2)÷3]×9
9
=2992(平方米)
方法二:(90﹣2)×(36﹣2)
=88×34
=2992(平方米)
答:草坪的实际面积是2992平方米。
【点评】本题考查组合图形的面积,求出每一小块草坪的长和宽,进而求出一块的面积,然后再求总面积是解题的关键。
30.校园内有一个梯形花圃,这个梯形上底长27米,下底长38米,高24米。其中有一块三角形的地方种植郁金香(如图阴影部分),其他地方种植了月季花。月季花的种植面积是多少平方米?
【答案】456平方米。
【分析】通过观察图形可知,种月季花的两部分(两个三角形)的底等于梯形的下底,高等于梯形的高,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:38×24÷2
=912÷2
=456(平方米)
答:月季花的种植面积是456平方米。
【点评】此题主要考查梯形、三角形面积公式的灵活运用,关键是熟记公式。
31.某实验小学有一块劳动实践基地(如图)。这块地的面积是多少平方米?
【答案】见试题解答内容
【分析】通过观察图形可知,把这块地的面积分成一个梯形和一个三角形,根据梯形的面积公式:S=(a+b)h÷2,三角形的面积公式:S=ah÷2,把数据代入公式求出它们的面积和即可。
【解答】解:(2+8)×8÷2+8×6÷2
=10×8÷2+48÷2
=40+24
=64(平方米)
答:这块地的面积是64平方米。
【点评】此题主要考查梯形、三角形面积公式的灵活运用,关键是熟记公式。
32.如图是一个长28米、宽22米的花坛,在这个花坛的四周要修宽3米的小路。小路的面积是多少平方米?
【答案】336平方米。
【分析】根据小路的面积等于长为(28+3×2),宽为(22+3×2)的长方形的面积减花坛的面积;据此解答即可。
【解答】解:(28+3×2)×(22+3×2)﹣28×22
=(28+6)×(22+6)﹣616
=34×28﹣616
=952﹣616
=336(平方米)
答:小路的面积是336平方米。
【点评】本题主要考查了组合图形的面积,解题的关键是确定大长方形的长与宽。
33.如图所示,正方形ABCD边长为10,正方形BEFG边长为6,正方形JIHC面积未知,则阴影部分的面积是多少?
【答案】20。
【分析】通过观察图形,分别连接FC、CI,DF与CI平行,所以三角形DFI与三角形DFC的面积相等,正方形ABCD边长为10,正方形BEFG边长为6,所以EC=AD﹣BE=10﹣6=4,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:如图:
正方形ABCD边长为10,正方形BEFG边长为6,
所以EC=AD﹣BE=10﹣6=4
由于DF与CI平行,所以△DFI的面积与△DFC的面积相等。
而△DFC的面积为,
所以△DFI的面积也为20。
【点评】此题主要利用等积变形得出△DFI的面积与△DFC的面积相等。再利用三角形的面积公式解答。
34.用两块长方形纸片和一块正方形纸片拼成一个大正方形(如图),长方形纸片面积分别是44平方厘米和28平方厘米,原来正方形面积是多少平方厘米?
【答案】49平方厘米。
【分析】如图:要使构成的图形是正方形,那么两个长方形的宽就相等,而且大长方形的长就是大正方形的边长,设它们的宽是x厘米,那么小长方形的长就是(28÷x)厘米,小长方形的长加上大长方形的宽就是大长方形的边长,由此列出方程求出长方形的宽,进而求出长方形的长,得出小正方形的边长,然后根据正方形的面积=边长×边长,把数据代入公式解答。
【解答】解:设长方形的宽为x厘米,
(28÷x)+x=44÷x
28+x2=44
x2=16
x=4
大长方形的长是:44÷4=11(厘米)
小正方形的边长是:11﹣4=7(厘米)
小正方形的面积是:7×7=49(平方厘米)
答:正方形纸片的面积是49平方厘米。
【点评】此题主要考查长方形、正方形面积公式的灵活应用,关键是熟记公式,重点是找出两个长方形的长宽与大正方形的边长之间的关系。
35.将一个边长为10厘米的正方形纸对折后剪去一个上底是2.5厘米,下底是5厘米,高是2厘米的梯形,然后打开(如图所示),求剩下部分的面积.
【答案】见试题解答内容
【分析】将一个边长为10厘米的正方形纸对折后剪去一个上底是2.5厘米,下底是5厘米,高是2厘米的梯形,打开后,求剩下的面积利用正方形面积减去2个上底是2.5厘米,下底是5厘米,高是2厘米的梯形的面积公式代入数值求解即可.
【解答】解:10×10﹣(2.5+5)×2÷2×2
=100﹣15
=85(平方厘米)
答:剩下部分的面积是85平方厘米.
【点评】此题主要考查正方形和梯形的面积公式的计算应用.
36.李叔叔要粉刷一面墙(如图),如果粉刷1平方米墙需用涂料800g,那么粉刷这面墙一共需要多少千克的涂料?
【答案】28.8千克。
【分析】这面墙有一个长方形和一个三角形组成,长方形的长等于三角形的底,利用长方形和三角形的面积公式求出总面积,再乘粉刷1平方米墙需用涂料的千克数即可求解。
【解答】解:800克=0.8千克
(8×3.6+8×1.8÷2)×0.8
=(28.8+7.2)×0.8
=36×0.8
=28.8(千克)
答:粉刷这面墙一共需要28.8千克涂料。
【点评】解答此题的关键是求出这个图形的面积。
37.如图是同一块草地的占地平面图。(单位:m)
(1)要算它的占地面积,你有几种割补方法?请在图中画出相应的虚线。(备用图若不够,可画草图来补充)
(2)它的占地面积有多大?(选一种来计算,先说明选的是图几)
【答案】(1)
(2)3240平方米。
【分析】(1)①可以分成一个三角形和一个长方形;②可以分成一个梯形和一个长方形;③可以分成一个三角形和一个梯形;④可以分成3个三角形;⑤可以利用填补法,补上一个梯形。
【解答】解:(1)作图如下:
(2)选择图①。(答案不唯一)
(60﹣30)×(72﹣48)÷2+60×48
=30×24÷2+2880
=360+2880
=3240(平方米)
答:它的占地面积是3240平方米。
【点评】此题考查的目的是理解掌握利用“割补”法、“填补”法求组合图形面积的方法及应用。
38.如图,长方形ABCD中,线段AB长8cm,线段BC长15cm.四边形EFGH的面积是9cm2,涂色部分的面积是多少?
【答案】69cm2.
【分析】要求涂色部分的面积,可以用长方形ABCD的面积减去三角形BDF和三角形AFC的面积,但此时,三角形BDF和三角形AFC重合的部分,即四边形EFGH的面积重复减去了2次,需要再加上四边形EFGH的面积;三角形BDF和三角形AFC高都是AB,底相加等于BC的长,根据三角形面积公式:Sah,两个三角形的面积和AB×BFAB×FCAB×(BF+FC)AB BC,据此列式计算.
【解答】解:涂色部分的面积为:
8×1515×8+9
=120﹣60+9
=69(cm2)
答:涂色部分的面积是69cm2.
【点评】本题主要考查了组合图形的面积,将要求的不规则部分的面积转化规则图形的面积的差或和,是本题解题的关键.
39.两张边长都为6cm的正方形纸片,分别按如图剪下不同规格的圆片.哪张纸片剩下的废料(阴影部分)多?
【答案】同样多。
【分析】通过观察图形可知,左图中阴影部分的面积等于正方形的减去圆的面积,右图中阴影部分的面积等于正方形的面积减去4个等圆的面积,根据正方形的面积公式:S=a2,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:6×6﹣3.14×(6÷2)2
=36﹣3.14×9
=36﹣28.26
=7.74(平方厘米)
6×6﹣3.14×(6÷2÷2)2×4
=36﹣3.14×2.25×4
=36﹣28.16
=7.74(平方厘米)
答:两张纸剩下的废料同样多。
【点评】此题主要考查正方形的面积公式、圆的面积公式的灵活运用,关键是熟记公式。
40.“月季花展”是人民公园的特色之一,如图是人民公园的地图,为了估算人民公园的面积,田田勾画出下面的图形(如左图),并用地图的测距工具测出所需的数据(如右图)。请你帮助田田算一算人民公园的面积。
(1)你想怎样求这个图形的面积?在如右图中画一画。
(2)按照你的想法算出人民公园的面积是多少平方米?
【答案】(1);(2)125580平方米。
【分析】(1)可以把公园分为平行四边形和梯形两部分;
(2)根据平行四边形和梯形的面积公式求解即可。
【解答】解:(1)如图:
(2)(216+160+500)×140÷2+306×210
=876×140÷2+64260
=61320+64260
=125580(平方米)
答:人民公园的面积是125580平方米。
【点评】此题主要考查的是梯形和平行四边形的面积公式,解题的关键是把不规则图形转化为规则图形。
41.潍坊萝卜,又称潍县萝卜,素有“烟台苹果、莱阳梨、不如潍县萝卜皮”之说,深受人们的喜爱。
张伯伯承包了一块不规则的萝卜地,萝卜地形状如图所示,张伯伯想把这块地分成两块,一块是梯形,种水果青萝卜;一块是三角形,种冰糖心萝卜。请你帮张伯伯在图中分一分,算一算,每块萝卜地的面积是多少公顷?
【答案】0.65公顷,0.525公顷。
【分析】根据梯形的面积公式:S=(a+b)h÷2,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:如图:
(30+100)×100÷2
=130×100÷2
=13000÷2
=6500(平方米)
150×(100﹣30)÷2
=150×70×2
=10500÷2
=5250(平方米)
6500平方米=0.65公顷
5250平方米=0.525公顷
答:梯形萝卜地的面积是0.65公顷,三角形萝卜地的面积是0.525公顷。
【点评】此题主要考查梯形、三角形面积公式的灵活运用,关键是熟记公式。
42.如图:一个长方形铁皮,剪下一个正方形后,剩余的面积是61平方厘米,剪下的正方形的面积是多少?
【答案】16平方厘米。
【分析】通过观察图形可知,阴影部分的面积可以分成两个长方形的面积,设剪下的正方形的边长为x 厘米,则阴影部分的=7×(x+3)+3x,据此列方程求出正方形的边长,再根据正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:设剪下的正方形的边长为x 厘米
7×(x+3)+3x=61
7x+21+3x=61
10x+21=61
10x+21﹣21=61﹣21
10x=40
10x÷4=40÷4
x=4
4×4=16(平方厘米)
答:剪下的正方形的面积是16平方厘米。
【点评】此题主要考查正方形、长方形面积公式的灵活运用,关键是熟记公式。
43.市民广场中一个正方形花坛的四周有一条2米宽的石子路,石子路的总面积是48平方米,中间花坛的面积是多少平方米?
【答案】16平方米。
【分析】根据题意,将石子路的面积分成4个相同的宽是2米的长方形,每个长方形的面积是48÷4=12(平方米),根据长方形面积=长×宽,据此可以求出每个长方形的长,每个长方形的长减去2米就是中间花坛的边长,然后根据正方形的面积=边长×边长,把数据代入公式解答。
【解答】解:如图:
48÷4=12(平方米)
12÷2=6(米)
6﹣2=4(米)
4×4=16(平方米)
答:中间花坛的面积是16平方米。
【点评】此题主要考查长方形、正方形面积公式的灵活运用,关键是求出中间正方形花坛的边长。
44.下面是一批小麦地的平面图。如果每平方米收小麦1.5千克。这块地可收小麦多少千克?
【答案】6187.5千克。
【分析】根据平行四边形的面积公式:S=ab,三角形的面积公式:S=ah÷2,把数据代入公式求出这块地的面积,然后用这块地的面积乘每平方米收小麦的质量即可。
【解答】解:(75×40+75×30÷2)×1.5
=(3000+1125)×1.5
=4125×1.5
=6187.5(千克)
答:这块地可收小麦6187.5千克。
【点评】此题主要考查平行四边形、三角形面积公式的灵活运用,关键是熟记公式。
45.在一块平行四边形空地上种植一些草皮,空地中间留有一条2米宽的小路,
上面铺设了彩砖供人行走。(如图)
(1)需要种植草皮的面积有多大?
(2)如果每平方米草皮需要13元,每平方米彩砖需要24元,那么铺完这块空地共需要多少元?
【答案】见试题解答内容
【分析】(1)将右侧部分平移到左侧部分相接,可以组成一个底为(12+8)m,高为8米的平行四边形,根据平行四边形面积公式:S=ah,代入数值计算即可;
(2)根据(1)的结果,再乘草皮的单价即为草皮的花费,小路的面积为底为2m,高为8米的平行四边形面积,再乘单价求出彩砖的花费,两种花费相加即可。
【解答】解:(1)(12+8)×8
=20×8
=160(m2)
答:需要种植草皮的面积有160平方米。
(2)160×13+2×8×24
=2080+16×24
=2080+384
=2464(元)
答:铺完这块空地共需要2464元。
【点评】本题主要考查了组合图形的面积,通过平移来简化问题是本题解题的关键。
46.如图,一块长方形草地,长方形的长是16米,宽是10米,中间铺了一条2米宽的石子路。那么草地部分面积有多大?
【答案】128平方米。
【分析】通过观察图形,把小路两边草地通过平移转化为一个长是16米,宽是(10﹣2)米的长方形的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:16×(10﹣2)
=16×8
=128(平方米)
答:草地部分的面积有128平方米。
【点评】此题解答关键是通过平移将小路两边的草地拼成一个长方形,根据长方形的面积公式解答。
47.学校学农基地有一块菜地(如图所示),这块菜地有多少平方米?如果每平方米菜地产生25元收益,这块菜地一共可以产生收益多少元?
【答案】1330平方米;33250元。
【分析】如解答中图形,根据这块菜地的面积等于两个长方形的面积和,求出这块地的面积,再乘25,即可求出这块菜地一共产生的收益。
【解答】解:如图:
48×19+(41﹣19)×19
=912+22×19
=912+418
=1330(平方米)
1330×25=33250(元)
答:这块菜地有1330平方米,一共可以产生收益33250元。
【点评】本题主要考查了组合图形的面积,解题的关键是把不规则图形的面积转化为规则图形的面积。
48.近年来我国新能源汽车发展迅速。某市开发区新建一处新能源汽车销售中心(如图所示)。这个销售中心的占地面积是多少平方米?(用两种方法解答)
【答案】5270平方米。
【分析】根据图形的特点,可以分成一个梯形和一个长方形,也可以用填补法,用大长方形的面积减去补上的三角形的面积,根据梯形的面积公式:S=(a+b)h÷2,长方形的面积公式:S=ab,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:如图:
方法一:
(48+70)×(80﹣50)÷2+70×50
=118×30÷2+3500
=1770+3500
=5270(平方米)
方法二:80×70﹣(70﹣48)×(80﹣50)÷2
=5600﹣22×30÷2
=5600﹣330
=5270(平方米)
答:这个销售中心的占地面积是5270平方米。
【点评】此题考查的目的是理解掌握利用“分割”法、“填补”法求组合图形的面积。
49.市政府准备在街心花园建一个花圃(见图).这个花圃需要占地多少平方米?
【答案】见试题解答内容
【分析】根据图示,用长是26米、宽是13米的长方形的面积加上长是34米、宽是13米的长方形的面积,求出这个花圃需要占地多少平方米即可.
【解答】解:26×13+34×13
=(26+34)×13
=60×13
=780(平方米)
答:这个花圃需要占地780平方米.
【点评】此题主要考查了组合图形的面积的求法,解答此题的关键是要熟练掌握长方形的面积的求法.
50.一块近似平行四边形的草坪,中间有一条石子路(如图)。如果铺1平方米草坪需要7.5元,铺这块草坪大约需要多少钱?
【答案】855元。
【分析】将两边草地向中间平移,可得底为20﹣1=19(米),高为6米的平行四边形草地,再根据平行四边形面积公式求出草坪的面积,用草坪的面积乘1平方米草坪的价格,就是铺这块草坪需要的总钱数。
【解答】解:(20﹣1)×6
=19×6
=114(平方米)
114×7.5=855(元)
答:铺这块草坪大约需要855元。
【点评】解答此题的关键是根据平行四边形的面积公式求出草坪的面积。
51.已知甲的面积比乙的面积大57平方厘米,半圆的直径是20厘米,求BC的长.
【答案】见试题解答内容
【分析】甲的面积比乙的面积大57平方厘米,也就是说半圆的面积比三角形的面积大57平方厘米,用半圆的面积减去57就是三角形的面积,再用三角形的面积乘以2除以20就是BC的长度.
【解答】解:△ABC的面积是:
3.14×(20÷2)2÷2﹣57,
=314÷2﹣57,
=157﹣57,
=100(平方厘米);
BC的长是:
100×2÷20,
=200÷20,
=10(厘米);
答:BC的长10厘米.
【点评】本题运用圆的面积公式及三角形的面积公式进行解答即可.
52.如图,单位厘米,求图中阴影部分的周长是多少厘米?
【答案】30.84厘米。
【分析】通过观察图形可知,阴影部分的等于直径是8厘米的圆周长的一半加上直径是4厘米的圆周长的一半,再加上两个半圆的直径,根据圆的周长公式:C=πd,把数据代入公式解答。
【解答】解:3.14×8÷2+3.14×4÷2+8+4
=12.56+6.28+8+4
=81.84+8+4
=30.84(厘米)
答:阴影部分的周长是30.84厘米。
【点评】此题考查的目的是理解半圆周长的意义,掌握半圆的周长公式及应用。
53.小强有一个平行四边形玩具(如图),已知阴影部分三角形的面积是6平方分米,空白部分(梯形)小强用来摆拼图,摆拼图部分的面积是多少平方分米?
【答案】26平方分米。
【分析】先根据三角形的面积公式S=ah÷2,求出三角形的高,即平行四边形的高,根据平行四边形的面积公式:S=ah,求出平行四边形的面积,再用平行四边形的面积减三角形的面积即可。
【解答】解:三角形的高:6×2÷3=4(分米)
8×4﹣6
=32﹣6
=26(平方分米)
答:摆拼图部分的面积是26平方分米。
【点评】本题主要考查了组合图形的面积,解题的关键是求出三角形的高。
54.如图,一块平行四边形的草地中间有一条长8米,宽1米的长方形小路。草地种草部分的面积是多少平方米?
【答案】112平方米。
【分析】草地的面积等于整块地的面积减去小路的面积,根据平行四边形的面积公式:S=ah,长方形的面积公式:S=ab,把数据代入公式求出它们的面积差即可。
【解答】解:15×8﹣8×1
=120﹣8
=112(平方米)
答:草地的面积是112平方米。
【点评】此题主要考查平行四边形、长方形面积公式的灵活运用,关键是熟记公式。
55.如图,长方形ABCD的长是16厘米,宽是12厘米,BE=15厘米,CF和BE垂直,那么CF的长是多少厘米?
【答案】见试题解答内容
【分析】如图:连接CE,根据三角形的面积公式:sah,已知AD=BC=16厘米,AB=CD=12厘米,BE=15厘米,由此可以求出△BCE的面积,又知在△BCE中,高CF对应的底BE等于15厘米,根据三角形的面积公式得:高(CF)=2S÷BE,据此解答即可.
【解答】解:如图:
连接 CE,
则△BCEBC×CD
16×12
=96(平方厘米),
因为△BCEBE×CF,
所以BE×CF=96,
所以CF=96×2÷15
=192÷15
=12.8(厘米),
答:CF的长是12.8厘米.
【点评】此题主要考查三角形面积公式的灵活运用,关键是熟记公式,
56.比一比,谁的面积大?
【答案】甲的面积大。
【分析】根据利用数方格计算图形面积的方法,不满格的按半个计算,据此分别求出两个图形的面积,然后进行比较即可。
【解答】解:甲的面积是15.5;
乙的面积是14;
15.5>14
答:甲的面积大。
【点评】此题考查的目的是理解掌握利用数方格计算图形面积的方法及应用。
57.一个站台的横截面如图,已知梯形的上底是2.1米,下底是3.4米,涂色阴影部分面积为4.76平方米,求梯形的面积是多少平方米?如果按这个面积涂颜料,每平方米需要涂料1.5千克,求剩下的部分还需要多少千克涂料?
【答案】7.7平方米,4.41千克。
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,据此求出高,然后把数据代入公式求出空白部分三角形的面积,涂色部分的面积加上空白部分的面积就是梯形的面积,再用空白部分的面积乘每平方米用涂料的质量即可。
【解答】解:4.76×2÷3.4
=9.52÷3.4
=2.8(米)
2.1×2.8÷2
=5.88÷2
=2.94(平方米)
4.76+2.94=7.7(平方米)
2.94×1.5=4.41(千克)
答:梯形的面积是7.7平方米,剩下的部分还需要4.41千克涂料。
【点评】此题主要考查三角形、梯形面积公式的灵活运用,关键是熟记公式。
58.如图所示,学校在一块长方形的空地上围了一个直径是8米的半圆形花坛,把剩余地方(阴影部分)铺成了草坪。花坛的面积和草坪的周长分别是多少?
【答案】花坛的面积是25.12平方米,草坪的周长是28.56米。
【分析】(1)花坛的面积=半圆的面积,根据圆的面积公式:S=πr2求解即可;
(2)根据草坪的周长=长方形的长+长方形的宽×2+圆周长的一半,找入数据求解即可。
【解答】解:3.14×(8÷2)2÷2
=3.14×16÷2
=50.24÷2
=25.12(平方米)
(8÷2)×2+8+3.14×8÷2
=8+8+12.56
=28.56(米)
答:花坛的面积是25.12平方米,草坪的周长是28.56米。
【点评】此题考查了组合图形的面积的计算方法,一般都是转化到规则图形中,利用周长公式计算解答。
59.一块近似长方形的平地,中间有一块近似三角形草地,现在三角形草地之外其余部分种上竹子,如果每平方米竹子造价30元,这块竹林大约需要多少钱?
【答案】见试题解答内容
【分析】根据长方形的面积公式;S=ab求出长方形的面积,再根据三角形的面积公式:S=ah÷2求出草地的面积再相减,求出其余部分的面积,再根据总价=单价×数量解答即可.
【解答】解:15×8﹣7.5×8÷2
=120﹣30
=90(平方米)
90×30=2700(元)
答:这块竹林大约需要2700元钱.
【点评】本题的重点是求出空地的面积,再根据总价=单价×数量解答.
60.如图是一张长方形卡纸和一张三角形卡纸部分重叠在一起后得到的图形。已知长方形卡纸的面积比三角形卡纸的面积小16平方厘米,你能算出线段CE的长度吗?(单位:厘米)
【答案】10厘米。
【分析】根据长方形的面积公式:S=ab,三角形的面积公式:S=ab÷2,那么a=2S÷h,把数据代入公式求出长方形的面积,长方形的面积加上16平方厘米就是三角形的面积,再求出三角形的底(DE),然后用DE的长减去DC的长就是CE的长。
【解答】解:(8×6+16)×2÷8﹣6
=(48+16)×2÷8﹣6
=64×2÷8﹣6
=128÷8﹣6
=16﹣6
=10(厘米)
答:线段CE的长度10厘米。
【点评】此题主要考查长方形的面积公式、三角形的面积公式的灵活运用,关键是熟记公式。
21世纪教育网(www.21cnjy.com)
1.李伯伯家有如图所示的两块菜地,其中一块平行四边形地种青菜,另一块三角形地种萝卜。这两块地的总面积是多少平方米?
2.如图,这是一枚“外圆内方”的古钱币,该钱币外圆的周长为9.42厘米,中间正方形孔的边长为1厘米,如果把这枚钱币放在桌面上,它所覆盖的面积是多少平方厘米?(π值取3.14)
3.某开发区大标语牌上要画出如图所示的三种标点符号:句号、逗号、问号。已知大圆半径相同,都为R;小圆半径也相同,都为r;而且R:r=2:1.如果都是均匀用料,画哪个标点符号的油漆用得最多?
4.24小时开放的“河东驿站”,为广大市民提供了取暖纳凉、歇脚喝水等便利服务,被誉为深夜依旧为您亮灯的“家”。如图是某驿站的平面图,请你用喜欢的方法算一算这个驿站的占地面积是多少?
5.如图,长方形ABCD的长是12米,宽是6米,E、F分别是长方形CD边和AD边上的中点,涂色部分的面积是多少平方米?
6.某小区一块长方形的绿地的造型如图所示(单位:m),其中两个扇形表示绿地,两块绿地用五彩石隔开,那么需铺多大面积的五彩石?(保留π)
7.刘叔叔新买了一套住房,平面图如图。
(单位:米)他在装修时遇到了一些问题:
(1)这套房子一共有多少平方米?
(2)如果用复合地板铺“南卧室”,每平方米售价60元,一共需要多少元?
8.一块平行四边形的草坪中有一块宽0.6米,长15米的水渠(如图),这块草坪的面积是多少平方米?
9.两个长12cm、宽8cm的长方形(如图)摆放后,组合图形的面积是多少?
10.张奶奶家原有一块三角形菜地(如图中最大的三角形),由于公路拓宽,菜地被占用了一部分,剩下的菜地面积为40平方米。如果占用每平方米菜地国家给予225元的赔偿金,那么张奶奶家一共可以得到多少元赔偿金?
11.绿地公园内有一块梯形的空地上种了3种花,为了便于游人观赏花卉,修建了一条2米宽的小路(图中阴影部分)。这块空地上种花的面积是多少?
12.剪纸是中国古老的民间艺术之一。下面是小玲剪的一个花边图形,你能计算出阴影部分的面积吗?
13.如图中阴影部分的面积占正方形面积的百分之几?
14.此图四边形ABCD是平行四边形,BC长为12厘米,阴影部分的面积是 平方厘米。
15.如图,一块长25米,宽18米的长方形草地上有两条宽2米的小路,草坪的面积是多少?
16.如图所示,在正方形ABCD中,红色、绿色正方形面积分别是52和13,且红、绿两个正方形有一个点重合,黄色正方形的一个顶点位于红色正方形两个对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,那么黄色正方形的面积是多少?
17.如图是房屋的侧面墙,砌墙时每平方米用砖135块,两面这样的墙共需用多少块砖?
18.李叔叔家有一块菜地(如图),这块菜地的面积有多少平方米?
19.如图是一个扇形,圆心角是90°。四边形OCDE是一个正方形,它的对角线CE是4厘米。求阴影部分的面积。
20.一张长方形彩纸,长16厘米,宽12厘米,以相邻的一条长和一条宽的中点为端点连一条线段,沿该线段剪去一个角(如图),剩下的面积是多少平方厘米?
21.如图,王叔叔用9.42米长的篱笆靠墙围了一个最大的养鸡场,这个养鸡场的面积是多少平方米?如果每只鸡占地0.2平方米,这个养鸡场最多可以养多少只鸡?(根据实际情况,结果保留整数)
22.一块长方形空地因建房子被占掉一部分,剩下部分的面积(如图阴影所示)是多少平方米?
23.中国建筑中经常见到“外方内圆”和“外圆内方”的设计。如图中两个圆的直径都是4厘米,分别计算正方形和圆之间的部分各是多少平方厘米?
24.在小区空地上修一条长方形和一条平行四边形的小路,再在涂色部分种上花草,种花草的面积是多少平方米?合多少公顷?
25.如图,大正方形的边长是14厘米,小正方形的边长是10厘米。求阴影部分的面积。
26.学校有一块劳动基地,现将它划分成三部分分别用来种玉米、红薯、棉花,如图。
(1)种玉米的面积是多少平方米?
(2)如果每平方米种3棵棉花,一共能种多少棵棉花?
27.公园要进行绿化,在一个花坛(如图)中种绿植(涂色部分)。已知每平方米绿植需要12元,则给这个花坛种绿植需要花费多少钱?
28.一块草坪被4条1米宽的小路平均分成了9小块,草坪的面积是多少平方米?
29.如图,一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
30.校园内有一个梯形花圃,这个梯形上底长27米,下底长38米,高24米。其中有一块三角形的地方种植郁金香(如图阴影部分),其他地方种植了月季花。月季花的种植面积是多少平方米?
31.某实验小学有一块劳动实践基地(如图)。这块地的面积是多少平方米?
32.如图是一个长28米、宽22米的花坛,在这个花坛的四周要修宽3米的小路。小路的面积是多少平方米?
33.如图所示,正方形ABCD边长为10,正方形BEFG边长为6,正方形JIHC面积未知,则阴影部分的面积是多少?
34.用两块长方形纸片和一块正方形纸片拼成一个大正方形(如图),长方形纸片面积分别是44平方厘米和28平方厘米,原来正方形面积是多少平方厘米?
35.将一个边长为10厘米的正方形纸对折后剪去一个上底是2.5厘米,下底是5厘米,高是2厘米的梯形,然后打开(如图所示),求剩下部分的面积.
36.李叔叔要粉刷一面墙(如图),如果粉刷1平方米墙需用涂料800g,那么粉刷这面墙一共需要多少千克的涂料?
37.如图是同一块草地的占地平面图。(单位:m)
(1)要算它的占地面积,你有几种割补方法?请在图中画出相应的虚线。(备用图若不够,可画草图来补充)
(2)它的占地面积有多大?(选一种来计算,先说明选的是图几)
38.如图,长方形ABCD中,线段AB长8cm,线段BC长15cm.四边形EFGH的面积是9cm2,涂色部分的面积是多少?
39.两张边长都为6cm的正方形纸片,分别按如图剪下不同规格的圆片.哪张纸片剩下的废料(阴影部分)多?
40.“月季花展”是人民公园的特色之一,如图是人民公园的地图,为了估算人民公园的面积,田田勾画出下面的图形(如左图),并用地图的测距工具测出所需的数据(如右图)。请你帮助田田算一算人民公园的面积。
(1)你想怎样求这个图形的面积?在如右图中画一画。
(2)按照你的想法算出人民公园的面积是多少平方米?
41.潍坊萝卜,又称潍县萝卜,素有“烟台苹果、莱阳梨、不如潍县萝卜皮”之说,深受人们的喜爱。
张伯伯承包了一块不规则的萝卜地,萝卜地形状如图所示,张伯伯想把这块地分成两块,一块是梯形,种水果青萝卜;一块是三角形,种冰糖心萝卜。请你帮张伯伯在图中分一分,算一算,每块萝卜地的面积是多少公顷?
42.如图:一个长方形铁皮,剪下一个正方形后,剩余的面积是61平方厘米,剪下的正方形的面积是多少?
43.市民广场中一个正方形花坛的四周有一条2米宽的石子路,石子路的总面积是48平方米,中间花坛的面积是多少平方米?
44.下面是一批小麦地的平面图。如果每平方米收小麦1.5千克。这块地可收小麦多少千克?
45.在一块平行四边形空地上种植一些草皮,空地中间留有一条2米宽的小路,
上面铺设了彩砖供人行走。(如图)
(1)需要种植草皮的面积有多大?
(2)如果每平方米草皮需要13元,每平方米彩砖需要24元,那么铺完这块空地共需要多少元?
46.如图,一块长方形草地,长方形的长是16米,宽是10米,中间铺了一条2米宽的石子路。那么草地部分面积有多大?
47.学校学农基地有一块菜地(如图所示),这块菜地有多少平方米?如果每平方米菜地产生25元收益,这块菜地一共可以产生收益多少元?
48.近年来我国新能源汽车发展迅速。某市开发区新建一处新能源汽车销售中心(如图所示)。这个销售中心的占地面积是多少平方米?(用两种方法解答)
49.市政府准备在街心花园建一个花圃(见图).这个花圃需要占地多少平方米?
50.一块近似平行四边形的草坪,中间有一条石子路(如图)。如果铺1平方米草坪需要7.5元,铺这块草坪大约需要多少钱?
51.已知甲的面积比乙的面积大57平方厘米,半圆的直径是20厘米,求BC的长.
52.如图,单位厘米,求图中阴影部分的周长是多少厘米?
53.小强有一个平行四边形玩具(如图),已知阴影部分三角形的面积是6平方分米,空白部分(梯形)小强用来摆拼图,摆拼图部分的面积是多少平方分米?
54.如图,一块平行四边形的草地中间有一条长8米,宽1米的长方形小路。草地种草部分的面积是多少平方米?
55.如图,长方形ABCD的长是16厘米,宽是12厘米,BE=15厘米,CF和BE垂直,那么CF的长是多少厘米?
56.比一比,谁的面积大?
57.一个站台的横截面如图,已知梯形的上底是2.1米,下底是3.4米,涂色阴影部分面积为4.76平方米,求梯形的面积是多少平方米?如果按这个面积涂颜料,每平方米需要涂料1.5千克,求剩下的部分还需要多少千克涂料?
58.如图所示,学校在一块长方形的空地上围了一个直径是8米的半圆形花坛,把剩余地方(阴影部分)铺成了草坪。花坛的面积和草坪的周长分别是多少?
59.一块近似长方形的平地,中间有一块近似三角形草地,现在三角形草地之外其余部分种上竹子,如果每平方米竹子造价30元,这块竹林大约需要多少钱?
60.如图是一张长方形卡纸和一张三角形卡纸部分重叠在一起后得到的图形。已知长方形卡纸的面积比三角形卡纸的面积小16平方厘米,你能算出线段CE的长度吗?(单位:厘米)
期末专项培优 解决问题的策略
参考答案与试题解析
1.李伯伯家有如图所示的两块菜地,其中一块平行四边形地种青菜,另一块三角形地种萝卜。这两块地的总面积是多少平方米?
【答案】100平方米。
【分析】通过观察图形可知,这两个底拼成一个梯形,梯形的上底是(9.3+6.4)米,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【解答】解:(9.3+6.4+9.3)×8÷2
=25×8÷2
=200÷2
=100(平方米)
答:这两个地的总面积是100平方米。
【点评】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
2.如图,这是一枚“外圆内方”的古钱币,该钱币外圆的周长为9.42厘米,中间正方形孔的边长为1厘米,如果把这枚钱币放在桌面上,它所覆盖的面积是多少平方厘米?(π值取3.14)
【答案】6.065平方厘米。
【分析】通过观察图形可知,阴影部分的面积等于圆的面积减去正方形的面积,根据圆的面积公式:S=πr2,正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:3.14×(9.42÷3.14÷2)2﹣1×1
=3.14×2.25﹣1
=7.065﹣1
=6.065(平方厘米)
答:它所覆盖的面积是6.065平方厘米。
【点评】此题主要考查圆的面积公式、正方形的面积公式的灵活运用,关键是熟记公式。
3.某开发区大标语牌上要画出如图所示的三种标点符号:句号、逗号、问号。已知大圆半径相同,都为R;小圆半径也相同,都为r;而且R:r=2:1.如果都是均匀用料,画哪个标点符号的油漆用得最多?
【答案】问号。
【分析】根据环形面积公式:S=π(R2﹣r2),把数据代入公式求出句号的面积;逗号的面积通过旋转转化为大半圆的面积,问号的面积等于环形的面积加上小圆的面积,根据圆的公式:S=πr2,把数据代入公式求出它们的面积,然后进行比较即可。
【解答】解:设r为1,则R为2,
句号的面积:
π×(22﹣12)
=π×(4﹣1)
=π×3
=3π
逗号的面积:
π×22÷2
=π×4÷2
=2π
问号的面积:
π×(22﹣12)π×12
=π×(4﹣1)π×1
π+π
π
π>3π>2π
答:问号的油漆用量最多。
【点评】解答求组合图形的面积,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答。
4.24小时开放的“河东驿站”,为广大市民提供了取暖纳凉、歇脚喝水等便利服务,被誉为深夜依旧为您亮灯的“家”。如图是某驿站的平面图,请你用喜欢的方法算一算这个驿站的占地面积是多少?
【答案】97平方米。
【分析】根据图形的特点,可以分成一个正方形和一个长方形,根据正方形的面积公式:S=a2,长方形的面积公式:S=ab,把数据代入公式求出它们的面积和即可。
【解答】解:如图:
(11﹣4)×7+12×4
=7×7+48
=49+48
=97(平方米)
答:这个驿站的占地面积是97平方米。
【点评】此题主要考查正方形、长方形面积公式的灵活运用,关键是熟记公式。
5.如图,长方形ABCD的长是12米,宽是6米,E、F分别是长方形CD边和AD边上的中点,涂色部分的面积是多少平方米?
【答案】36平方米。
【分析】连接BD,E、F分别是长方形CD边和AD边上的中点,则三角形BDE面积=三角形BCE的面积,三角形BDF的面积=三角形ABF的面积,所以涂色部分的面积等于长方形面积的一半,据此解答即可。
【解答】解:如图:
连接BD,E、F分别是长方形CD边和AD边上的中点,则三角形BDE面积=三角形BCE的面积,三角形BDF的面积=三角形ABF的面积,所以涂色部分的面积等于长方形面积的一半,
12×6÷2
=72÷2
=36(平方米)
答:涂色部分的面积是36平方米。
【点评】解答求不规则图形的面积,关键是通过“转化”,把不规则图形转化为规则图形进行解答。
6.某小区一块长方形的绿地的造型如图所示(单位:m),其中两个扇形表示绿地,两块绿地用五彩石隔开,那么需铺多大面积的五彩石?(保留π)
【答案】见试题解答内容
【分析】通过观察图形发现,铺五彩石的面积等于长方形的面积减去两个扇形的面积,根据长方形的面积公式:S=ab,圆的面积公式:S=πr2,把数据分别代入公式解答.
【解答】解:(a+b)×aπa2πb2
=a2+abπa2πb2(平方米)
答:需要铺(a2+abπa2πb2)平方米五彩石.
【点评】解答求组合图形的面积,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答.
7.刘叔叔新买了一套住房,平面图如图。
(单位:米)他在装修时遇到了一些问题:
(1)这套房子一共有多少平方米?
(2)如果用复合地板铺“南卧室”,每平方米售价60元,一共需要多少元?
【答案】(1)88平方米;
(2)1200元。
【分析】(1)先求出这套房子的长、宽,然后根据长方形的面积=长×宽,把数据代入公式解答。
(2)根据长方形的面积=长×宽,求出南卧室的面积,然后根据单价×数量=总价,列式解答。
【解答】解:(1)(5+1+5)×(4+4)
=11×8
=88(平方米)
答:这套房子一共有88平方米。
(2)5×4×60
=20×60
=1200(元)
答:一共需要1200元。
【点评】此题主要考查长方形面积公式的灵活应用,以及单价、数量、总价三者之间的关系及应用,关键是熟记公式。
8.一块平行四边形的草坪中有一块宽0.6米,长15米的水渠(如图),这块草坪的面积是多少平方米?
【答案】666平方米。
【分析】整块草坪是个平行四边形,水渠是个长方形,且长方形的长是平行四边形的高,草坪面积=平行四边形﹣长方形面积,平行四边形面积=底×高,长方形面积=长×宽,据此列式解答。
【解答】解:45×15﹣15×0.6
=675﹣9
=666(平方米)
答:这块草坪的面积是666平方米。
【点评】此题主要考查平行四边形的面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
9.两个长12cm、宽8cm的长方形(如图)摆放后,组合图形的面积是多少?
【答案】128平方厘米。
【分析】根据组合图形的面积=大长方形的面积+一个小长方形的面积,据此求解即可。
【解答】解:12×8+(12﹣8)×8
=96+4×8
=96+32
=128(平方厘米)
答:组合图形的面积是128平方厘米。
【点评】本题主要考查了组合图形,解题的关键是求出小长方形的长与宽。
10.张奶奶家原有一块三角形菜地(如图中最大的三角形),由于公路拓宽,菜地被占用了一部分,剩下的菜地面积为40平方米。如果占用每平方米菜地国家给予225元的赔偿金,那么张奶奶家一共可以得到多少元赔偿金?
【答案】3375元。
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,据此求出高,把数据代入公式求出被占用的面积,然后再乘每平方米的赔偿金即可。
【解答】解:40×2÷8
=80÷8
=10(米)
3×10÷2×225
=15×225
=3375(元)
答:张奶奶家一共可以得到3375元赔偿金。
【点评】此题主要考查三角形面积公式的灵活运用,关键是熟记公式。
11.绿地公园内有一块梯形的空地上种了3种花,为了便于游人观赏花卉,修建了一条2米宽的小路(图中阴影部分)。这块空地上种花的面积是多少?
【答案】84平方米。
【分析】观察图形可知,这块空地上种花的面积=梯形的面积﹣长方形的面积,根据梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,代入数据计算即可求解。
【解答】解:(12+20)×6÷2﹣6×2
=32×6÷2﹣12
=96﹣12
=84(平方米)
答:这块空地上种花的面积是84平方米。
【点评】此题主要考查梯形、长方形面积公式的灵活运用,关键是熟记公式。
12.剪纸是中国古老的民间艺术之一。下面是小玲剪的一个花边图形,你能计算出阴影部分的面积吗?
【答案】16平方厘米。
【分析】通过观察图形可知,阴影部分的面积可以通过平移“转化”为边长是2厘米的4个正方形的面积。根据正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:2×2×4
=4×4
=16(平方厘米)
答:阴影部分的面积是16平方厘米。
【点评】此题解答的关键是通过“转化”把阴影部分的面积转化为4个正方形的面积,根据正方形的面积公式解答。
13.如图中阴影部分的面积占正方形面积的百分之几?
【答案】50%。
【分析】通过观察可知,图中正方形被平均分成两份,两个圆正好等于一个半圆,所以阴影部分的面积占正方形面积的一半;据此解答即可。
【解答】解:1÷2=50%
答:阴影部分的面积占正方形面积的50%。
【点评】解答本题的关键是理解两个圆正好等于一个半圆。
14.此图四边形ABCD是平行四边形,BC长为12厘米,阴影部分的面积是 36 平方厘米。
【答案】36。
【分析】把左边的阴影部分旋转到右边,可得:阴影部分的面积=平行四边形的一半,据此求解即可。
【解答】解:如图:
12×(12÷2)÷2
=12×6÷2
=36(平方厘米)
答:阴影部分的面积是36平方厘米。
故答案为:36。
【点评】本题主要考查了组合图形的面积,解题的关键是把不规则图形的面积转化为规则图形的面积。
15.如图,一块长25米,宽18米的长方形草地上有两条宽2米的小路,草坪的面积是多少?
【答案】368平方米。
【分析】根据图形的特点,可以通过平移把小路两边的草坪合并为长(25﹣2)米,宽(18﹣2)米的长方形,根据长方形的面积=长×宽,把数据代入公式解答。
【解答】解:(25﹣2)×(18﹣2)
=23×16
=368(平方米)
答:草坪的面积是368平方米。
【点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式。
16.如图所示,在正方形ABCD中,红色、绿色正方形面积分别是52和13,且红、绿两个正方形有一个点重合,黄色正方形的一个顶点位于红色正方形两个对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,那么黄色正方形的面积是多少?
【答案】见试题解答内容
【分析】如图:因为黄色正方形的两个顶点均位于两个正方形两条对角线的交点,所以②的面积是:52÷4=13,④的面积是:13÷4=3.25,所以④的面积:②的面积=3.25:13=1:4=1:22,由于边长的平方比等于面积比,则①的面积:④的面积=②的面积:③的面积=1:2,所以①的面积=③的面积=3.25×2=6.5,然后把①②③④的面积相加即可求出黄色正方形的面积.据此解答.
【解答】解:如图:根据分析得:
②的面积是:52÷4=13,
④的面积是:13÷4=3.25,
所以④的面积:②的面积=3.25:13=1:4=1:22,
由于边长的平方比等于面积比,则①的面积:④的面积=②的面积:③的面积=2:1,
所以①的面积=③的面积=3.25×2=6.5,
黄色正方形的面积是:6.5+13+6.5+3.25=29.25.
答:黄色正方形的面积是29.25.
【点评】此题重点考查学生对图形的分析能力,对于此类问题,应认真分析图意,找出各图形之间的关系;本题关键是明确:边长的平方比等于面积比.
17.如图是房屋的侧面墙,砌墙时每平方米用砖135块,两面这样的墙共需用多少块砖?
【答案】7128块砖。
【分析】先依据三角形和长方形的面积公式求出这面墙的面积,再乘2即两面墙的面积,然后乘每平方米需要的砖的块数,问题即可得解。
【解答】解:(6×1.2÷2+6×3.8)×2×135
=(3.6+22.8)×2×135
=26.4×2×135
=7128(块)
答:两面这样的墙共需用7128块砖。
【点评】此题主要考查三角形和长方形的面积的计算方法在实际生活中的应用。
18.李叔叔家有一块菜地(如图),这块菜地的面积有多少平方米?
【答案】240平方米。
【分析】根据题意可知,这块菜地的面积等于两块长方形菜地的面积的和,一块长方形菜地的长为23米,宽为6米;另一块长方形菜地的长为17米,宽为6米,长方形的面积=长×宽,依此计算并解答即可。
【解答】解:如图:
23×6=138(平方米)
17×6=102(平方米)
138+102=240(平方米)
答:这块菜地的面积有240平方米。
【点评】熟练掌握长方形的面积的计算是解答此题的关键。
19.如图是一个扇形,圆心角是90°。四边形OCDE是一个正方形,它的对角线CE是4厘米。求阴影部分的面积。
【答案】8.56平方厘米。
【分析】因为CE是正方形OCDE的对角线,所以OD=CE=4(厘米),即扇形所在圆的半径为4厘米,再根据阴影部分的面积=扇形的面积﹣空白三角形的面积,据此求解即可。
【解答】解:三角形COE的高是OD的一半,即CE的一半,4÷2=2(厘米)
3.14×42÷4﹣4×(4÷2)÷2
=3.14×16÷4﹣4×2÷2
=12.56﹣4
=8.56(平方厘米)
答:阴影部分的面积是8.56平方厘米。
【点评】本题主要考查了组合图形的面积,解题的关键把不规则图形转化为规则图形。
20.一张长方形彩纸,长16厘米,宽12厘米,以相邻的一条长和一条宽的中点为端点连一条线段,沿该线段剪去一个角(如图),剩下的面积是多少平方厘米?
【答案】168平方厘米。
【分析】通过观察图形可知,剩下部分的面积等于长方形的面积减去三角形的面积,根据长方形的面积公式:S=ab,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:16×12﹣(16÷2)×(12÷2)÷2
=192﹣8×6÷2
=192﹣24
=168(平方厘米)
答:剩下的面积是168平方米。
【点评】此题主要考查长方形、三角形面积公式的灵活运用,关键是熟记公式。
21.如图,王叔叔用9.42米长的篱笆靠墙围了一个最大的养鸡场,这个养鸡场的面积是多少平方米?如果每只鸡占地0.2平方米,这个养鸡场最多可以养多少只鸡?(根据实际情况,结果保留整数)
【答案】28.26平方米,141只。
【分析】通过观察图形可知,两面靠墙,用9.42米篱笆围成一个圆的养鸡场,根据圆的周长公式:C=2πr,那么r=C÷π÷2,据此可以求出半径,再根据圆的面积公式:S=πr2,求出养鸡场的面积,然后根据“包含”除法的意义,用除法解答。
【解答】解:9.42×4÷3.14÷2
=37.68÷3.14÷2
=12÷2
=6(米)
3.14×62
=3.14×36
=28.26(平方米)
28.26÷0.2≈141(只)
答:这个养鸡场的面积是28.26平方米,这个养鸡场最多可以养141只鸡。
【点评】此题主要考查圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式,重点是求出养鸡场的半径。
22.一块长方形空地因建房子被占掉一部分,剩下部分的面积(如图阴影所示)是多少平方米?
【答案】1200平方米。
【分析】根据阴影部分的面积=长方形的面积﹣三角形的面积,据此求解即可。
【解答】解:50×(12+18)﹣50×12÷2
=50×30﹣600÷2
=1500﹣300
=1200(平方米)
答:剩下部分的面积(如图阴影所示)是1200平方米。
【点评】本题主要考查了组合图形的面积,解题的关键是把不规则图形的面积转化为规则图形的面积。
23.中国建筑中经常见到“外方内圆”和“外圆内方”的设计。如图中两个圆的直径都是4厘米,分别计算正方形和圆之间的部分各是多少平方厘米?
【答案】(1)3.44平方厘米;(2)4.56平方厘米。
【分析】(1)由图示可知,圆的直径等于正方形的边长,正方形和圆之间的部分的面积等于正方形的面积减去圆的面积;
(2)根据图示,把正方形分成两个等腰直角三角形,三角形的底等于圆的直径,三角形的高等于圆的半径。正方形和圆之间的部分的面积等于圆的面积减去正方形的面积。
利用正方形面积公式:S=a2,圆的面积公式:S=πr2,三角形面积公式:S=ah÷2,计算即可。
【解答】解:(1)4×4﹣3.14×(4÷2)2
=16﹣12.56
=3.44(平方厘米)
答:正方形和圆之间的部分的面积是3.44平方厘米。
(2)3.14×(4÷2)2﹣4÷2×2×4÷2
=12.56﹣8
=4.56(平方厘米)
答:正方形和圆之间的部分的面积是4.56平方厘米。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
24.在小区空地上修一条长方形和一条平行四边形的小路,再在涂色部分种上花草,种花草的面积是多少平方米?合多少公顷?
【答案】200000平方米,2公顷。
【分析】根据图形的特点,可以通过平移把涂色的三部分拼成一个底是(40+160)米,高是100米的平行四边形的面积,根据平行四边形的面积公式:S=ah,把数据代入公式解答。
【解答】解:(40+160)×100
=200×100
=20000(平方米)
20000平方米=2公顷
答:种花草的面积是20000平方米,合2公顷。
【点评】此题主要考查平行四边形面积公式的灵活运用,关键是熟记公式,重点是通过平移把涂色部分的面积拼成一个平行四边形的面积。
25.如图,大正方形的边长是14厘米,小正方形的边长是10厘米。求阴影部分的面积。
【答案】98平方厘米。
【分析】通过观察图形可知,阴影部分的面积等于长(14+10)厘米,宽14厘米的长方形的面积减去空白部分3个三角形的面积,根据长方形的面积公式;S=ab,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:(14+10)×14﹣14×14÷2﹣(14+10)×10÷2﹣(14﹣10)×10÷2
=24×14﹣196÷2﹣24×10÷2﹣4×10÷2
=336﹣98﹣120﹣20
=98(平方厘米)
答:阴影部分的面积是98平方厘米。
【点评】解答求组合图形的面积,关键是观察分析图形是由哪几部分组成的,是各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答。
26.学校有一块劳动基地,现将它划分成三部分分别用来种玉米、红薯、棉花,如图。
(1)种玉米的面积是多少平方米?
(2)如果每平方米种3棵棉花,一共能种多少棵棉花?
【答案】(1)9平方米;
(2)99棵。
【分析】(1)根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
(2)根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式求出棉花地的面积,然后再乘每平方米种棉花的棵数即可。
【解答】解:3×6÷2
=18÷2
=9(平方米)
答:玉米地的面积是9平方米。
(2)(4+7)×6÷2×3
=11×6÷2×3
=33×3
=99(棵)
答:一共能种99棵棉花。
【点评】此题主要考查三角形、梯形面积公式的灵活运用,关键是熟记公式。
27.公园要进行绿化,在一个花坛(如图)中种绿植(涂色部分)。已知每平方米绿植需要12元,则给这个花坛种绿植需要花费多少钱?
【答案】768元。
【分析】通过观察图形可知,可以通过平移转化为一个边长是(2×4)米的正方形的面积,根据正方形的面积公式:S=a2,把数据代入公式求出花坛的面积,然后再乘每平方米的费用即可。
【解答】解:(2×4)×(2×4)×12
=8×8×12
=64×12
=768(元)
答:给这个花坛种绿植需要花费768元。
【点评】解答求不规则图形的面积,关键是通过“转化”,把不规则图形转化为规则图形进行解答。
28.一块草坪被4条1米宽的小路平均分成了9小块,草坪的面积是多少平方米?
【答案】见试题解答内容
【分析】一块草坪被4条1米宽的小路平均分成了9小块,分成的每一块草坪的长是(45﹣1×2)÷3米,宽是(27﹣1×2)÷3米,根据长方形的面积公式:S=ab求出一块的面积,再乘9即可.据此解答.
【解答】解:[(45﹣1×2)÷3]×[(27﹣1×2)÷3]×9
9
=1075(平方米)
答:草坪的实际面积是1075平方米.
【点评】本题的重点是求出每一小块草坪的长和宽,进而求出一块的面积,然后再求总面积.
29.如图,一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
【答案】2992米。
【分析】方法一:一块草坪被4条1米宽的小路平均分成了9小块,分成的每一块草坪的长是(90﹣1×2)÷3米,宽是(36﹣1×2)÷3米,根据长方形的面积公式:S=ab求出一块的面积,再乘9即可解答。
方法二:观察图形,通过平移可得草坪的面积实际上就是长为90﹣2=88(米)、宽为36﹣2=34(米)的长方形的面积,然后再根据长方形的面积公式:S=ab进行解答。
【解答】解:方法一:[(90﹣1×2)÷3]×[(36﹣1×2)÷3]×9
9
=2992(平方米)
方法二:(90﹣2)×(36﹣2)
=88×34
=2992(平方米)
答:草坪的实际面积是2992平方米。
【点评】本题考查组合图形的面积,求出每一小块草坪的长和宽,进而求出一块的面积,然后再求总面积是解题的关键。
30.校园内有一个梯形花圃,这个梯形上底长27米,下底长38米,高24米。其中有一块三角形的地方种植郁金香(如图阴影部分),其他地方种植了月季花。月季花的种植面积是多少平方米?
【答案】456平方米。
【分析】通过观察图形可知,种月季花的两部分(两个三角形)的底等于梯形的下底,高等于梯形的高,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:38×24÷2
=912÷2
=456(平方米)
答:月季花的种植面积是456平方米。
【点评】此题主要考查梯形、三角形面积公式的灵活运用,关键是熟记公式。
31.某实验小学有一块劳动实践基地(如图)。这块地的面积是多少平方米?
【答案】见试题解答内容
【分析】通过观察图形可知,把这块地的面积分成一个梯形和一个三角形,根据梯形的面积公式:S=(a+b)h÷2,三角形的面积公式:S=ah÷2,把数据代入公式求出它们的面积和即可。
【解答】解:(2+8)×8÷2+8×6÷2
=10×8÷2+48÷2
=40+24
=64(平方米)
答:这块地的面积是64平方米。
【点评】此题主要考查梯形、三角形面积公式的灵活运用,关键是熟记公式。
32.如图是一个长28米、宽22米的花坛,在这个花坛的四周要修宽3米的小路。小路的面积是多少平方米?
【答案】336平方米。
【分析】根据小路的面积等于长为(28+3×2),宽为(22+3×2)的长方形的面积减花坛的面积;据此解答即可。
【解答】解:(28+3×2)×(22+3×2)﹣28×22
=(28+6)×(22+6)﹣616
=34×28﹣616
=952﹣616
=336(平方米)
答:小路的面积是336平方米。
【点评】本题主要考查了组合图形的面积,解题的关键是确定大长方形的长与宽。
33.如图所示,正方形ABCD边长为10,正方形BEFG边长为6,正方形JIHC面积未知,则阴影部分的面积是多少?
【答案】20。
【分析】通过观察图形,分别连接FC、CI,DF与CI平行,所以三角形DFI与三角形DFC的面积相等,正方形ABCD边长为10,正方形BEFG边长为6,所以EC=AD﹣BE=10﹣6=4,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:如图:
正方形ABCD边长为10,正方形BEFG边长为6,
所以EC=AD﹣BE=10﹣6=4
由于DF与CI平行,所以△DFI的面积与△DFC的面积相等。
而△DFC的面积为,
所以△DFI的面积也为20。
【点评】此题主要利用等积变形得出△DFI的面积与△DFC的面积相等。再利用三角形的面积公式解答。
34.用两块长方形纸片和一块正方形纸片拼成一个大正方形(如图),长方形纸片面积分别是44平方厘米和28平方厘米,原来正方形面积是多少平方厘米?
【答案】49平方厘米。
【分析】如图:要使构成的图形是正方形,那么两个长方形的宽就相等,而且大长方形的长就是大正方形的边长,设它们的宽是x厘米,那么小长方形的长就是(28÷x)厘米,小长方形的长加上大长方形的宽就是大长方形的边长,由此列出方程求出长方形的宽,进而求出长方形的长,得出小正方形的边长,然后根据正方形的面积=边长×边长,把数据代入公式解答。
【解答】解:设长方形的宽为x厘米,
(28÷x)+x=44÷x
28+x2=44
x2=16
x=4
大长方形的长是:44÷4=11(厘米)
小正方形的边长是:11﹣4=7(厘米)
小正方形的面积是:7×7=49(平方厘米)
答:正方形纸片的面积是49平方厘米。
【点评】此题主要考查长方形、正方形面积公式的灵活应用,关键是熟记公式,重点是找出两个长方形的长宽与大正方形的边长之间的关系。
35.将一个边长为10厘米的正方形纸对折后剪去一个上底是2.5厘米,下底是5厘米,高是2厘米的梯形,然后打开(如图所示),求剩下部分的面积.
【答案】见试题解答内容
【分析】将一个边长为10厘米的正方形纸对折后剪去一个上底是2.5厘米,下底是5厘米,高是2厘米的梯形,打开后,求剩下的面积利用正方形面积减去2个上底是2.5厘米,下底是5厘米,高是2厘米的梯形的面积公式代入数值求解即可.
【解答】解:10×10﹣(2.5+5)×2÷2×2
=100﹣15
=85(平方厘米)
答:剩下部分的面积是85平方厘米.
【点评】此题主要考查正方形和梯形的面积公式的计算应用.
36.李叔叔要粉刷一面墙(如图),如果粉刷1平方米墙需用涂料800g,那么粉刷这面墙一共需要多少千克的涂料?
【答案】28.8千克。
【分析】这面墙有一个长方形和一个三角形组成,长方形的长等于三角形的底,利用长方形和三角形的面积公式求出总面积,再乘粉刷1平方米墙需用涂料的千克数即可求解。
【解答】解:800克=0.8千克
(8×3.6+8×1.8÷2)×0.8
=(28.8+7.2)×0.8
=36×0.8
=28.8(千克)
答:粉刷这面墙一共需要28.8千克涂料。
【点评】解答此题的关键是求出这个图形的面积。
37.如图是同一块草地的占地平面图。(单位:m)
(1)要算它的占地面积,你有几种割补方法?请在图中画出相应的虚线。(备用图若不够,可画草图来补充)
(2)它的占地面积有多大?(选一种来计算,先说明选的是图几)
【答案】(1)
(2)3240平方米。
【分析】(1)①可以分成一个三角形和一个长方形;②可以分成一个梯形和一个长方形;③可以分成一个三角形和一个梯形;④可以分成3个三角形;⑤可以利用填补法,补上一个梯形。
【解答】解:(1)作图如下:
(2)选择图①。(答案不唯一)
(60﹣30)×(72﹣48)÷2+60×48
=30×24÷2+2880
=360+2880
=3240(平方米)
答:它的占地面积是3240平方米。
【点评】此题考查的目的是理解掌握利用“割补”法、“填补”法求组合图形面积的方法及应用。
38.如图,长方形ABCD中,线段AB长8cm,线段BC长15cm.四边形EFGH的面积是9cm2,涂色部分的面积是多少?
【答案】69cm2.
【分析】要求涂色部分的面积,可以用长方形ABCD的面积减去三角形BDF和三角形AFC的面积,但此时,三角形BDF和三角形AFC重合的部分,即四边形EFGH的面积重复减去了2次,需要再加上四边形EFGH的面积;三角形BDF和三角形AFC高都是AB,底相加等于BC的长,根据三角形面积公式:Sah,两个三角形的面积和AB×BFAB×FCAB×(BF+FC)AB BC,据此列式计算.
【解答】解:涂色部分的面积为:
8×1515×8+9
=120﹣60+9
=69(cm2)
答:涂色部分的面积是69cm2.
【点评】本题主要考查了组合图形的面积,将要求的不规则部分的面积转化规则图形的面积的差或和,是本题解题的关键.
39.两张边长都为6cm的正方形纸片,分别按如图剪下不同规格的圆片.哪张纸片剩下的废料(阴影部分)多?
【答案】同样多。
【分析】通过观察图形可知,左图中阴影部分的面积等于正方形的减去圆的面积,右图中阴影部分的面积等于正方形的面积减去4个等圆的面积,根据正方形的面积公式:S=a2,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:6×6﹣3.14×(6÷2)2
=36﹣3.14×9
=36﹣28.26
=7.74(平方厘米)
6×6﹣3.14×(6÷2÷2)2×4
=36﹣3.14×2.25×4
=36﹣28.16
=7.74(平方厘米)
答:两张纸剩下的废料同样多。
【点评】此题主要考查正方形的面积公式、圆的面积公式的灵活运用,关键是熟记公式。
40.“月季花展”是人民公园的特色之一,如图是人民公园的地图,为了估算人民公园的面积,田田勾画出下面的图形(如左图),并用地图的测距工具测出所需的数据(如右图)。请你帮助田田算一算人民公园的面积。
(1)你想怎样求这个图形的面积?在如右图中画一画。
(2)按照你的想法算出人民公园的面积是多少平方米?
【答案】(1);(2)125580平方米。
【分析】(1)可以把公园分为平行四边形和梯形两部分;
(2)根据平行四边形和梯形的面积公式求解即可。
【解答】解:(1)如图:
(2)(216+160+500)×140÷2+306×210
=876×140÷2+64260
=61320+64260
=125580(平方米)
答:人民公园的面积是125580平方米。
【点评】此题主要考查的是梯形和平行四边形的面积公式,解题的关键是把不规则图形转化为规则图形。
41.潍坊萝卜,又称潍县萝卜,素有“烟台苹果、莱阳梨、不如潍县萝卜皮”之说,深受人们的喜爱。
张伯伯承包了一块不规则的萝卜地,萝卜地形状如图所示,张伯伯想把这块地分成两块,一块是梯形,种水果青萝卜;一块是三角形,种冰糖心萝卜。请你帮张伯伯在图中分一分,算一算,每块萝卜地的面积是多少公顷?
【答案】0.65公顷,0.525公顷。
【分析】根据梯形的面积公式:S=(a+b)h÷2,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:如图:
(30+100)×100÷2
=130×100÷2
=13000÷2
=6500(平方米)
150×(100﹣30)÷2
=150×70×2
=10500÷2
=5250(平方米)
6500平方米=0.65公顷
5250平方米=0.525公顷
答:梯形萝卜地的面积是0.65公顷,三角形萝卜地的面积是0.525公顷。
【点评】此题主要考查梯形、三角形面积公式的灵活运用,关键是熟记公式。
42.如图:一个长方形铁皮,剪下一个正方形后,剩余的面积是61平方厘米,剪下的正方形的面积是多少?
【答案】16平方厘米。
【分析】通过观察图形可知,阴影部分的面积可以分成两个长方形的面积,设剪下的正方形的边长为x 厘米,则阴影部分的=7×(x+3)+3x,据此列方程求出正方形的边长,再根据正方形的面积公式:S=a2,把数据代入公式解答。
【解答】解:设剪下的正方形的边长为x 厘米
7×(x+3)+3x=61
7x+21+3x=61
10x+21=61
10x+21﹣21=61﹣21
10x=40
10x÷4=40÷4
x=4
4×4=16(平方厘米)
答:剪下的正方形的面积是16平方厘米。
【点评】此题主要考查正方形、长方形面积公式的灵活运用,关键是熟记公式。
43.市民广场中一个正方形花坛的四周有一条2米宽的石子路,石子路的总面积是48平方米,中间花坛的面积是多少平方米?
【答案】16平方米。
【分析】根据题意,将石子路的面积分成4个相同的宽是2米的长方形,每个长方形的面积是48÷4=12(平方米),根据长方形面积=长×宽,据此可以求出每个长方形的长,每个长方形的长减去2米就是中间花坛的边长,然后根据正方形的面积=边长×边长,把数据代入公式解答。
【解答】解:如图:
48÷4=12(平方米)
12÷2=6(米)
6﹣2=4(米)
4×4=16(平方米)
答:中间花坛的面积是16平方米。
【点评】此题主要考查长方形、正方形面积公式的灵活运用,关键是求出中间正方形花坛的边长。
44.下面是一批小麦地的平面图。如果每平方米收小麦1.5千克。这块地可收小麦多少千克?
【答案】6187.5千克。
【分析】根据平行四边形的面积公式:S=ab,三角形的面积公式:S=ah÷2,把数据代入公式求出这块地的面积,然后用这块地的面积乘每平方米收小麦的质量即可。
【解答】解:(75×40+75×30÷2)×1.5
=(3000+1125)×1.5
=4125×1.5
=6187.5(千克)
答:这块地可收小麦6187.5千克。
【点评】此题主要考查平行四边形、三角形面积公式的灵活运用,关键是熟记公式。
45.在一块平行四边形空地上种植一些草皮,空地中间留有一条2米宽的小路,
上面铺设了彩砖供人行走。(如图)
(1)需要种植草皮的面积有多大?
(2)如果每平方米草皮需要13元,每平方米彩砖需要24元,那么铺完这块空地共需要多少元?
【答案】见试题解答内容
【分析】(1)将右侧部分平移到左侧部分相接,可以组成一个底为(12+8)m,高为8米的平行四边形,根据平行四边形面积公式:S=ah,代入数值计算即可;
(2)根据(1)的结果,再乘草皮的单价即为草皮的花费,小路的面积为底为2m,高为8米的平行四边形面积,再乘单价求出彩砖的花费,两种花费相加即可。
【解答】解:(1)(12+8)×8
=20×8
=160(m2)
答:需要种植草皮的面积有160平方米。
(2)160×13+2×8×24
=2080+16×24
=2080+384
=2464(元)
答:铺完这块空地共需要2464元。
【点评】本题主要考查了组合图形的面积,通过平移来简化问题是本题解题的关键。
46.如图,一块长方形草地,长方形的长是16米,宽是10米,中间铺了一条2米宽的石子路。那么草地部分面积有多大?
【答案】128平方米。
【分析】通过观察图形,把小路两边草地通过平移转化为一个长是16米,宽是(10﹣2)米的长方形的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:16×(10﹣2)
=16×8
=128(平方米)
答:草地部分的面积有128平方米。
【点评】此题解答关键是通过平移将小路两边的草地拼成一个长方形,根据长方形的面积公式解答。
47.学校学农基地有一块菜地(如图所示),这块菜地有多少平方米?如果每平方米菜地产生25元收益,这块菜地一共可以产生收益多少元?
【答案】1330平方米;33250元。
【分析】如解答中图形,根据这块菜地的面积等于两个长方形的面积和,求出这块地的面积,再乘25,即可求出这块菜地一共产生的收益。
【解答】解:如图:
48×19+(41﹣19)×19
=912+22×19
=912+418
=1330(平方米)
1330×25=33250(元)
答:这块菜地有1330平方米,一共可以产生收益33250元。
【点评】本题主要考查了组合图形的面积,解题的关键是把不规则图形的面积转化为规则图形的面积。
48.近年来我国新能源汽车发展迅速。某市开发区新建一处新能源汽车销售中心(如图所示)。这个销售中心的占地面积是多少平方米?(用两种方法解答)
【答案】5270平方米。
【分析】根据图形的特点,可以分成一个梯形和一个长方形,也可以用填补法,用大长方形的面积减去补上的三角形的面积,根据梯形的面积公式:S=(a+b)h÷2,长方形的面积公式:S=ab,三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:如图:
方法一:
(48+70)×(80﹣50)÷2+70×50
=118×30÷2+3500
=1770+3500
=5270(平方米)
方法二:80×70﹣(70﹣48)×(80﹣50)÷2
=5600﹣22×30÷2
=5600﹣330
=5270(平方米)
答:这个销售中心的占地面积是5270平方米。
【点评】此题考查的目的是理解掌握利用“分割”法、“填补”法求组合图形的面积。
49.市政府准备在街心花园建一个花圃(见图).这个花圃需要占地多少平方米?
【答案】见试题解答内容
【分析】根据图示,用长是26米、宽是13米的长方形的面积加上长是34米、宽是13米的长方形的面积,求出这个花圃需要占地多少平方米即可.
【解答】解:26×13+34×13
=(26+34)×13
=60×13
=780(平方米)
答:这个花圃需要占地780平方米.
【点评】此题主要考查了组合图形的面积的求法,解答此题的关键是要熟练掌握长方形的面积的求法.
50.一块近似平行四边形的草坪,中间有一条石子路(如图)。如果铺1平方米草坪需要7.5元,铺这块草坪大约需要多少钱?
【答案】855元。
【分析】将两边草地向中间平移,可得底为20﹣1=19(米),高为6米的平行四边形草地,再根据平行四边形面积公式求出草坪的面积,用草坪的面积乘1平方米草坪的价格,就是铺这块草坪需要的总钱数。
【解答】解:(20﹣1)×6
=19×6
=114(平方米)
114×7.5=855(元)
答:铺这块草坪大约需要855元。
【点评】解答此题的关键是根据平行四边形的面积公式求出草坪的面积。
51.已知甲的面积比乙的面积大57平方厘米,半圆的直径是20厘米,求BC的长.
【答案】见试题解答内容
【分析】甲的面积比乙的面积大57平方厘米,也就是说半圆的面积比三角形的面积大57平方厘米,用半圆的面积减去57就是三角形的面积,再用三角形的面积乘以2除以20就是BC的长度.
【解答】解:△ABC的面积是:
3.14×(20÷2)2÷2﹣57,
=314÷2﹣57,
=157﹣57,
=100(平方厘米);
BC的长是:
100×2÷20,
=200÷20,
=10(厘米);
答:BC的长10厘米.
【点评】本题运用圆的面积公式及三角形的面积公式进行解答即可.
52.如图,单位厘米,求图中阴影部分的周长是多少厘米?
【答案】30.84厘米。
【分析】通过观察图形可知,阴影部分的等于直径是8厘米的圆周长的一半加上直径是4厘米的圆周长的一半,再加上两个半圆的直径,根据圆的周长公式:C=πd,把数据代入公式解答。
【解答】解:3.14×8÷2+3.14×4÷2+8+4
=12.56+6.28+8+4
=81.84+8+4
=30.84(厘米)
答:阴影部分的周长是30.84厘米。
【点评】此题考查的目的是理解半圆周长的意义,掌握半圆的周长公式及应用。
53.小强有一个平行四边形玩具(如图),已知阴影部分三角形的面积是6平方分米,空白部分(梯形)小强用来摆拼图,摆拼图部分的面积是多少平方分米?
【答案】26平方分米。
【分析】先根据三角形的面积公式S=ah÷2,求出三角形的高,即平行四边形的高,根据平行四边形的面积公式:S=ah,求出平行四边形的面积,再用平行四边形的面积减三角形的面积即可。
【解答】解:三角形的高:6×2÷3=4(分米)
8×4﹣6
=32﹣6
=26(平方分米)
答:摆拼图部分的面积是26平方分米。
【点评】本题主要考查了组合图形的面积,解题的关键是求出三角形的高。
54.如图,一块平行四边形的草地中间有一条长8米,宽1米的长方形小路。草地种草部分的面积是多少平方米?
【答案】112平方米。
【分析】草地的面积等于整块地的面积减去小路的面积,根据平行四边形的面积公式:S=ah,长方形的面积公式:S=ab,把数据代入公式求出它们的面积差即可。
【解答】解:15×8﹣8×1
=120﹣8
=112(平方米)
答:草地的面积是112平方米。
【点评】此题主要考查平行四边形、长方形面积公式的灵活运用,关键是熟记公式。
55.如图,长方形ABCD的长是16厘米,宽是12厘米,BE=15厘米,CF和BE垂直,那么CF的长是多少厘米?
【答案】见试题解答内容
【分析】如图:连接CE,根据三角形的面积公式:sah,已知AD=BC=16厘米,AB=CD=12厘米,BE=15厘米,由此可以求出△BCE的面积,又知在△BCE中,高CF对应的底BE等于15厘米,根据三角形的面积公式得:高(CF)=2S÷BE,据此解答即可.
【解答】解:如图:
连接 CE,
则△BCEBC×CD
16×12
=96(平方厘米),
因为△BCEBE×CF,
所以BE×CF=96,
所以CF=96×2÷15
=192÷15
=12.8(厘米),
答:CF的长是12.8厘米.
【点评】此题主要考查三角形面积公式的灵活运用,关键是熟记公式,
56.比一比,谁的面积大?
【答案】甲的面积大。
【分析】根据利用数方格计算图形面积的方法,不满格的按半个计算,据此分别求出两个图形的面积,然后进行比较即可。
【解答】解:甲的面积是15.5;
乙的面积是14;
15.5>14
答:甲的面积大。
【点评】此题考查的目的是理解掌握利用数方格计算图形面积的方法及应用。
57.一个站台的横截面如图,已知梯形的上底是2.1米,下底是3.4米,涂色阴影部分面积为4.76平方米,求梯形的面积是多少平方米?如果按这个面积涂颜料,每平方米需要涂料1.5千克,求剩下的部分还需要多少千克涂料?
【答案】7.7平方米,4.41千克。
【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,据此求出高,然后把数据代入公式求出空白部分三角形的面积,涂色部分的面积加上空白部分的面积就是梯形的面积,再用空白部分的面积乘每平方米用涂料的质量即可。
【解答】解:4.76×2÷3.4
=9.52÷3.4
=2.8(米)
2.1×2.8÷2
=5.88÷2
=2.94(平方米)
4.76+2.94=7.7(平方米)
2.94×1.5=4.41(千克)
答:梯形的面积是7.7平方米,剩下的部分还需要4.41千克涂料。
【点评】此题主要考查三角形、梯形面积公式的灵活运用,关键是熟记公式。
58.如图所示,学校在一块长方形的空地上围了一个直径是8米的半圆形花坛,把剩余地方(阴影部分)铺成了草坪。花坛的面积和草坪的周长分别是多少?
【答案】花坛的面积是25.12平方米,草坪的周长是28.56米。
【分析】(1)花坛的面积=半圆的面积,根据圆的面积公式:S=πr2求解即可;
(2)根据草坪的周长=长方形的长+长方形的宽×2+圆周长的一半,找入数据求解即可。
【解答】解:3.14×(8÷2)2÷2
=3.14×16÷2
=50.24÷2
=25.12(平方米)
(8÷2)×2+8+3.14×8÷2
=8+8+12.56
=28.56(米)
答:花坛的面积是25.12平方米,草坪的周长是28.56米。
【点评】此题考查了组合图形的面积的计算方法,一般都是转化到规则图形中,利用周长公式计算解答。
59.一块近似长方形的平地,中间有一块近似三角形草地,现在三角形草地之外其余部分种上竹子,如果每平方米竹子造价30元,这块竹林大约需要多少钱?
【答案】见试题解答内容
【分析】根据长方形的面积公式;S=ab求出长方形的面积,再根据三角形的面积公式:S=ah÷2求出草地的面积再相减,求出其余部分的面积,再根据总价=单价×数量解答即可.
【解答】解:15×8﹣7.5×8÷2
=120﹣30
=90(平方米)
90×30=2700(元)
答:这块竹林大约需要2700元钱.
【点评】本题的重点是求出空地的面积,再根据总价=单价×数量解答.
60.如图是一张长方形卡纸和一张三角形卡纸部分重叠在一起后得到的图形。已知长方形卡纸的面积比三角形卡纸的面积小16平方厘米,你能算出线段CE的长度吗?(单位:厘米)
【答案】10厘米。
【分析】根据长方形的面积公式:S=ab,三角形的面积公式:S=ab÷2,那么a=2S÷h,把数据代入公式求出长方形的面积,长方形的面积加上16平方厘米就是三角形的面积,再求出三角形的底(DE),然后用DE的长减去DC的长就是CE的长。
【解答】解:(8×6+16)×2÷8﹣6
=(48+16)×2÷8﹣6
=64×2÷8﹣6
=128÷8﹣6
=16﹣6
=10(厘米)
答:线段CE的长度10厘米。
【点评】此题主要考查长方形的面积公式、三角形的面积公式的灵活运用,关键是熟记公式。
21世纪教育网(www.21cnjy.com)
