【期末专项培优】正比例和反比例(含解析)-2024-2025学年六年级下册数学苏教版
文档属性
| 名称 | 【期末专项培优】正比例和反比例(含解析)-2024-2025学年六年级下册数学苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-21 15:45:52 | ||
图片预览


文档简介
期末专项培优 正比例和反比例
1.一辆汽车两次行驶的路程与耗油量如下表:
行驶路程/km 24 96
耗油量/L 2 8
(1)分别写出每次行驶路程与耗油量的比值,判断这两个比能否组成比例.
(2)分别写出两次耗油量与对应行驶路程的比值,看看这两个比能否组成比例.
2.被除数一定,商和除数成 比例。
3.一种硬笔书法练习本,数量和总价的关系如表.
数量/本 1 2 3 4 5 6 …
总价/元 4 8 12 16 20 24 …
(1)在图中,描出总价与数量之间的对应点,并连接各点.
(2)总价与数量有什么关系?为什么?
4.如图的图象表示长颈鹿的奔跑情况.
(1)长颈鹿的奔跑路程与奔跑时间成 比例关系.
(2)请你计算一下,长颈鹿16分钟跑多少千米?
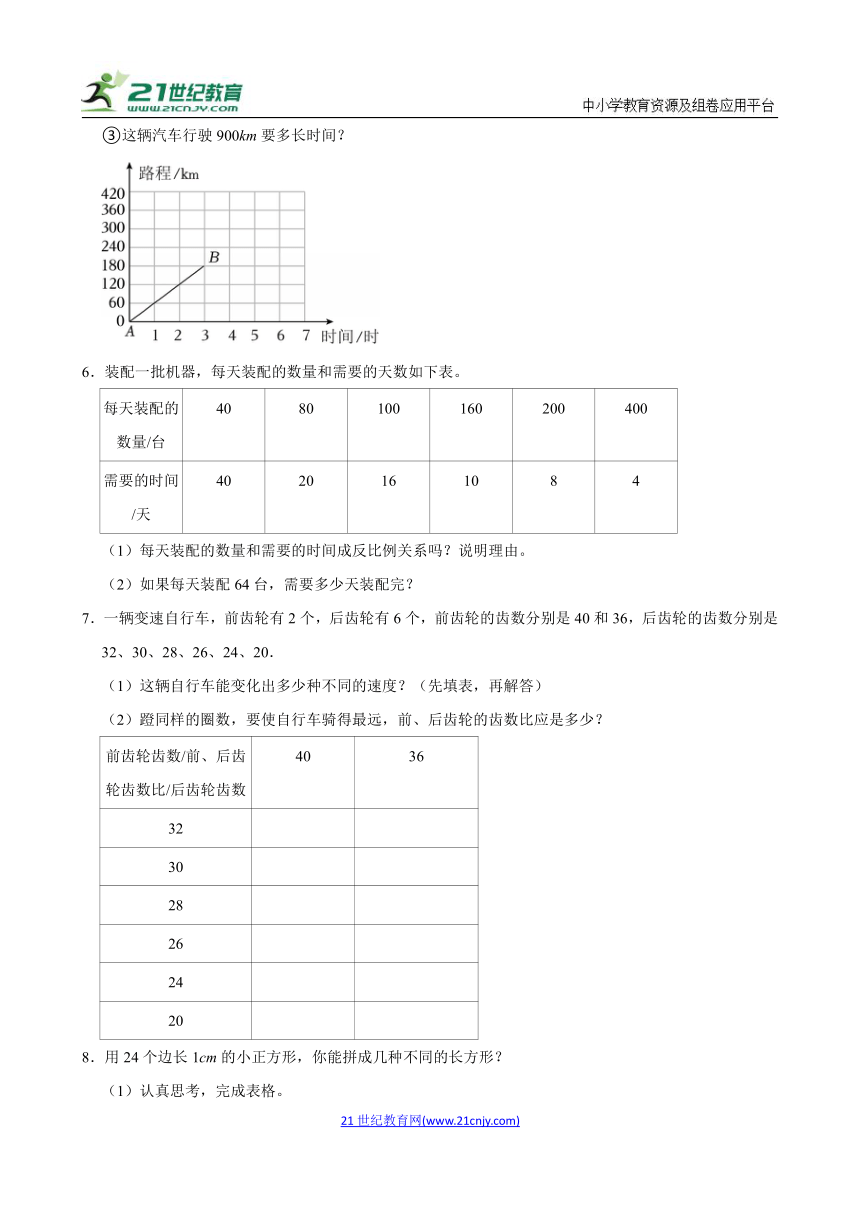
5.如图中线段AB表示一辆汽车行驶的路程与时间的关系.
①这辆汽车行驶了多长时间?行驶了多少千米?
②这辆汽车2.5小时行驶了多少千米?
③这辆汽车行驶900km要多长时间?
6.装配一批机器,每天装配的数量和需要的天数如下表。
每天装配的数量/台 40 80 100 160 200 400
需要的时间/天 40 20 16 10 8 4
(1)每天装配的数量和需要的时间成反比例关系吗?说明理由。
(2)如果每天装配64台,需要多少天装配完?
7.一辆变速自行车,前齿轮有2个,后齿轮有6个,前齿轮的齿数分别是40和36,后齿轮的齿数分别是32、30、28、26、24、20.
(1)这辆自行车能变化出多少种不同的速度?(先填表,再解答)
(2)蹬同样的圈数,要使自行车骑得最远,前、后齿轮的齿数比应是多少?
前齿轮齿数/前、后齿轮齿数比/后齿轮齿数 40 36
32
30
28
26
24
20
8.用24个边长1cm的小正方形,你能拼成几种不同的长方形?
(1)认真思考,完成表格。
长/cm
宽/cm
(2)从表中,你发现长和宽有怎样的比例关系?
9.四名同学都看了《少年学党史》这本书。请填写出每人看完这本书需要的天数。
郑小强 张小华 李小虹 王小新
每天看的页数 6 10 15 20
看的天数 30
照这样的速度看了3天,他们各看了多少页?还剩下多少页?
郑小强 张小华 李小虹 王小新
已看的页数
剩下的页数
题中,每天看的页数和看的天数 比例,已看的页数和剩下的页数 比例。
10.一列火车匀速行驶时,路程与时间的关系如表.
时间/小时 1 2 3 4 5 …
路程/千米 120 240 …
(1)完成上表.
(2)根据表格中的数据,这列火车行驶的路程与时间成什么比例?
(3)如果A、B两城相距420千米,需要多少小时可以从A城到达B城?
11.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量/辆 1 2 3 4 5 6 7
运货质量/吨 4 8 12 16 20 24 28
(1)表中 和 是两种相关联的量, 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
12.已知两个数M、N满足等式9N,数M与N成什么比例关系?请说明理由.
13.一辆汽车在高速公路上行驶的路程与耗油量的关系如下表:
行驶路程/km 50 100 150 200 250 …
耗油量/L 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来.
(2)这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350千米的耗油量.
(4)这辆汽车出发时油箱里有汽油40升,如果汽车要在高速公路上行驶460千米,你认为司机在途中需要加油吗?
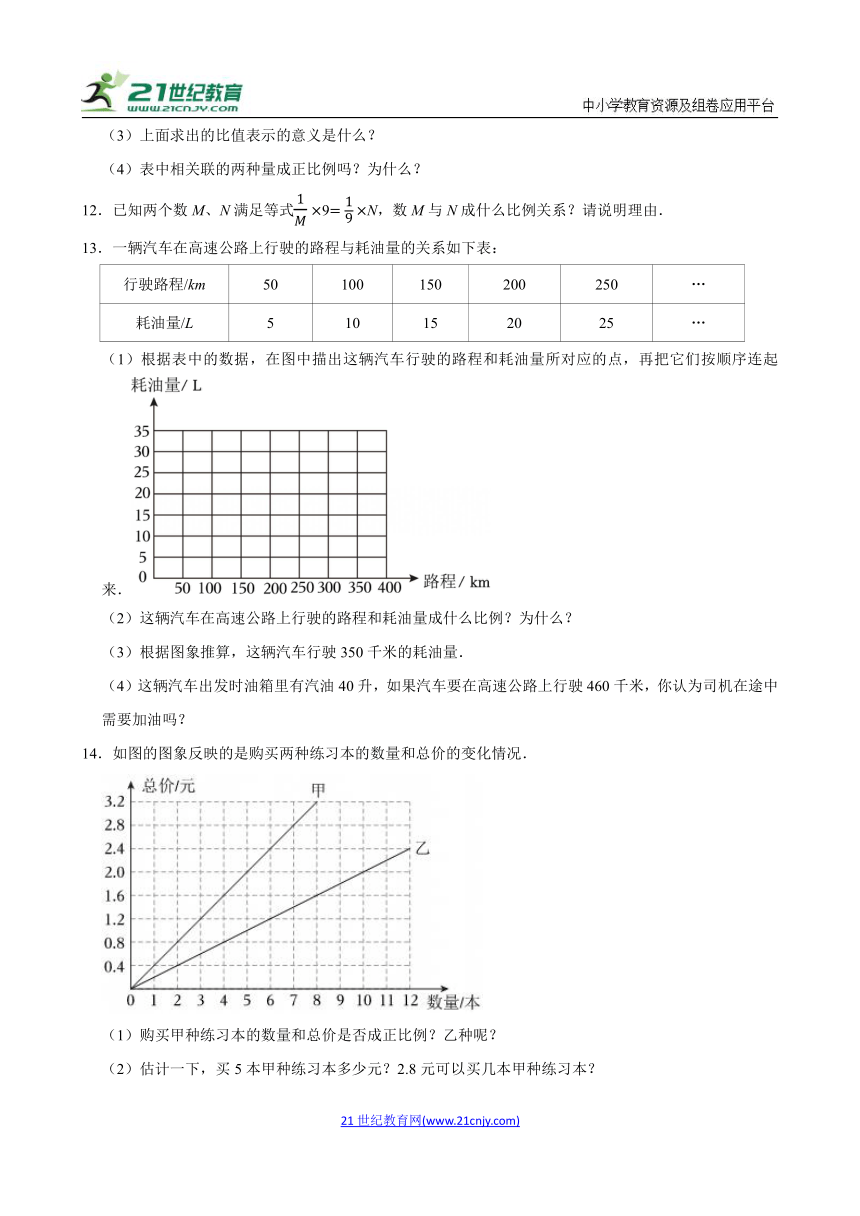
14.如图的图象反映的是购买两种练习本的数量和总价的变化情况.
(1)购买甲种练习本的数量和总价是否成正比例?乙种呢?
(2)估计一下,买5本甲种练习本多少元?2.8元可以买几本甲种练习本?
(3)从图上看哪种练习本便宜些?2.4元可以买两种练习本各多少本?
15.兰兰坐爸爸开的车去看爷爷,她每过10分钟看一次里程表上的读数,结果如下:
时间 9:10 9:20 9:30 9:40 9:50 …
里程表读数/km| 31220 31235 31250 31265 31280 …
(1)这辆汽车行驶的路程和时间之间有什么关系?它们成正比例关系吗?为什么?
(2)如果9:50时离爷爷家还有45千米,照这样的速度,他们在什么时刻可以到达爷爷家?
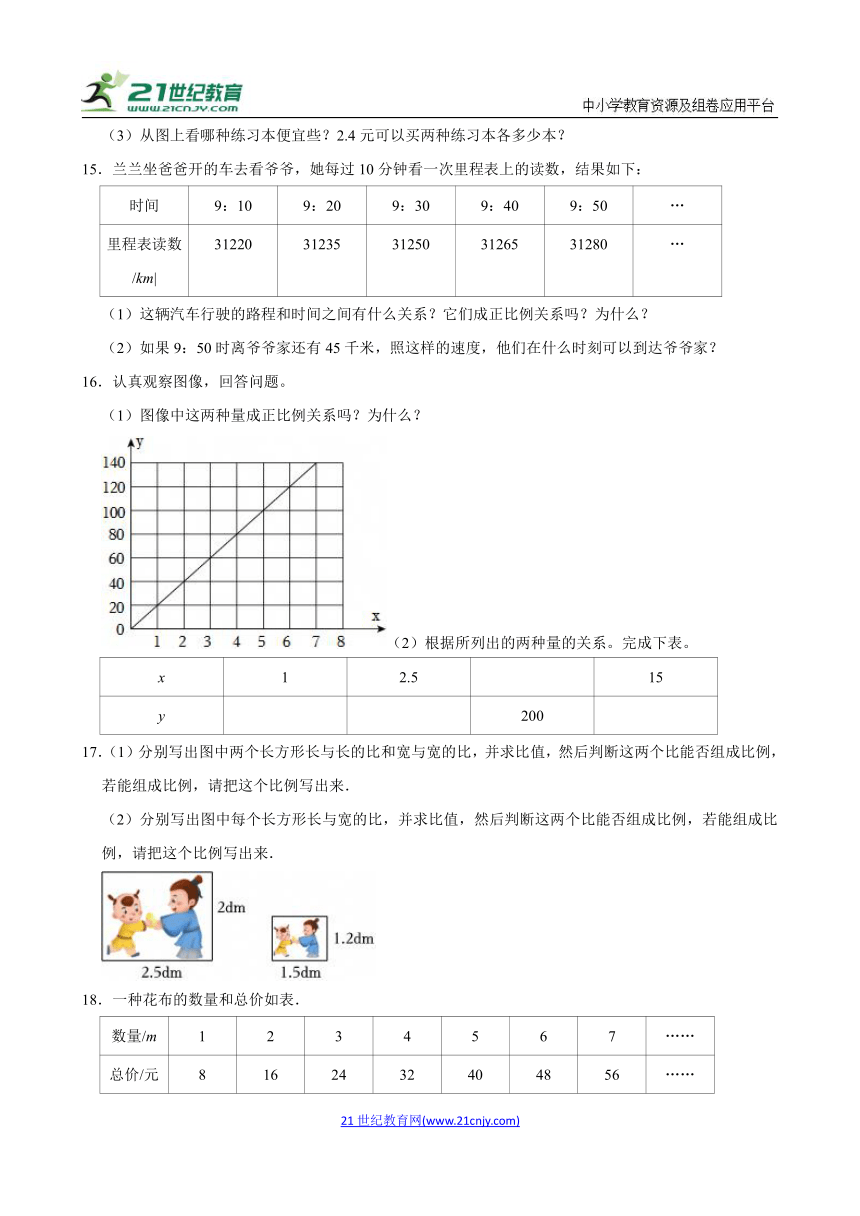
16.认真观察图像,回答问题。
(1)图像中这两种量成正比例关系吗?为什么?
(2)根据所列出的两种量的关系。完成下表。
x 1 2.5 15
y 200
17.(1)分别写出图中两个长方形长与长的比和宽与宽的比,并求比值,然后判断这两个比能否组成比例,若能组成比例,请把这个比例写出来.
(2)分别写出图中每个长方形长与宽的比,并求比值,然后判断这两个比能否组成比例,若能组成比例,请把这个比例写出来.
18.一种花布的数量和总价如表.
数量/m 1 2 3 4 5 6 7 ……
总价/元 8 16 24 32 40 48 56 ……
(1)表中的总价和数量成正比例关系吗?为什么?
(2)在如图中描出表示数量和对应总价的点,然后把它们连起来,并说说图象的特点.
(3)利用图象回答,买2.5m花布需要多少元?68元能买多少米花布?
19.妈妈带的钱可以买单价为30元的猪肉6kg或单价为60元的牛肉3kg。
(1)妈妈一共带了多少钱?
(2)如果买单价为72元的羊肉,可以买多少千克?
(3)总价一定时,单价和数量成什么比例?用等式表示出它们的关系。
20.一艘轮船从甲港开到乙港,3时行驶了75km.从乙港开到丙港,5时行驶了125km.
(1)分别求轮船从甲港开到乙港,从乙港开到丙港的速度.
(2)轮船行驶的路程和所用时间成什么比例?
(3)用等式把题目里的数量关系表示出来.
21.明明家的鱼缸有A,B两根进水管,先打开A管,中途打开B管。如图表示从开始加水到蓄满水的进水时间和鱼缸中水的体积的关系。
(1)从0分到6分,鱼缸中水的体积和进水时间成比例吗?如果成,成什么比例?如果不成比例,理由是什么?
(2)A管每分进水多少升?B管呢?
22.如图的图象反映的是老虎和狮子的食肉情况.
(1)老虎的食肉量与时间成正比例吗?狮子呢?
(2)估计一下,老虎和狮子8天各食肉多少千克?
(3)哪种动物每天的食肉量较少?
23.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是 元.
②12瓶的总价是 元.
③ 瓶的总价是36元.
24.某物流公司要将一批货物运往加工厂,如果要一次把这些货物全部运走,货车的载质量与所需车辆的数量如下表。
载质量/吨 2.5 3 5
数量/辆 48 40 24
(1)货车的载质量与所需车辆的数量成反比例吗?为什么?
(2)如果用载质量为4.8吨的货车来运,一共需要多少辆?
25.如图表示某工厂中甲、乙两个车间加工的零件数与时间的关系.
(1)乙车间生产的零件数与时间成正比例吗?为什么?
(2)如果生产8万个零件,那么乙车间比甲车间少用几个月?
26.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/cm2 900 1800 3600
所需地砖的数量/块 600 300 150
(1)所需地砖数量与每块地砖的面积成 比例关系。
(2)如果采用边长为50cm的方砖铺这间教室,需要多少块方砖?(用比例的方法解答)
27.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t 2.5 3 5 10
数量/辆 48 40
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
28.下面是某学校一个漏水的水龙头的滴水情况统计表。
滴水量/mL 20 40 60 80 100 ……
时间/分 1 2 3 4 5 ……
(1)滴水量和时间成 比例。
(2)这个水龙头每时滴水多少升?
(3)如果用一个底面积是10dm2,高是3dm的圆柱形水桶接漏的水,那么多长时间能接满?(水桶的厚度忽略不计)
29.判断下列各题中的两个量是否成比例关系.若成,成什么比例关系?
(1)每小时加工零件数一定,加工时间和加工零件总数.
(2)从甲地去乙地,已行的路程和未行的路程.
(3)圆的直径和周长.
(4)已知x(y≠0),x和y.
30.下面的图象表示小强从甲地到乙地不同的速度和所对应的时间。
(1)在这个过程中,哪种量没有变?
(2)速度和所对应的时间成什么比例关系?
(3)不计算,观察图象,如果每小时行40km,那么从甲地到乙地大约需要多少小时?
31.如图,甲、乙两车运货的吨数与次数的关系如图.
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
32.判断下面各题中的两种量是否成比例?成什么比例?为什么?
(1)小麦的出粉率一定,小麦的总重量和出粉的重量。
(2)每箱木瓜的个数一定,运来木瓜的箱数和木瓜的总个数。
(3)房间的面积一定,铺地砖的块数与每块地砖的面积。
33.把相同体积的水倒入底面积不同的杯子.
水的高度/cm 30 20 15 10 5 …
杯子的底面积/cm2 10 15 20 30 60 …
水的高度和杯子的底面积成反比例吗?为什么?
34.配制一种盐水,水的质量总是比盐水的质量少15%,盐的质量与盐水的质量成正比例吗?
35.某厂要生产一批豆浆机,平均每天产量和所需时间如表。
平均每天产量/台 200 300 500
所需时间/天 75 50 30
(1)平均每天产量和所需时间成 比例。
(2)现要在20天内完成生产任务,平均每天产量至少要达到多少台?
36.妈妈买来一袋橡皮泥,平平全部用来捏大小相同的圆锥,正好没有剩余.圆锥的个数与每个圆锥所用橡皮泥的体积是否成反比例?为什么?
37.某童车厂装配一批童车,每天装配的数量和需要的时间如表。
每天装配的数量/辆 60 90 120 180 360 …
时间/天 60 40 30 20 10 …
(1)判断每天装配的数量和时间是否成反比例,并说明理由。
(2)如果每天装配200辆,多少天可以装配完这批童车?
38.科技小组制作了一个弹簧秤,弹簧的长度是8厘米。经验证,弹簧的长度与所挂钩码的质量存在如下关系:
弹簧长度/cm 8 9 10 11 ……
钩码质量/kg 0 2 4 6 ……
(1)钩码的质量和弹簧伸长的长度成什么比例关系?
(2)小亮用科技小组制作的这个弹簧秤称一个物体,弹簧的长度是14.8cm,这个物体的质量是多少千克?(用比例知识解答)
39.判断下面每题中的两种量是不是成正比例,并说明理由.
(1)小新跳高的高度和他的身高.
(2)长方形的宽一定,它的面积和长.
(3)小麦每公顷产量一定,小麦的公顷数和总产量.
40.小牛和大牛吃肥肉,原来小牛和大牛吃的肉块数之比为2:5,后来小牛又吃了5块,大牛也又吃了2块,此时小牛和大牛吃的肉块数之比为5:9,求原来两人各自吃了多少块肥肉?
41.新冠肺炎疫情期间,口罩需求量大幅上升。某工厂接到任务紧急生产一批口罩,下面是每时生产口罩的数量与完成任务总共需要的时间的关系。
每时生产口罩的数量/万只 2 3 4 6
时间/时 72 48 36 24
(1)每时生产口罩的数量与时间有什么关系?(1分)
(2)如果每时生产8万只口罩,那么完成这项任务一共需要多少时?(4分)
42.用一些纸装订同样的练习本,每本用纸的张数和装订的本数如表。
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40
(1)将如表补充完整。
(2)每本用纸张数和装订本数是否成反比例关系?为什么?
(3)如果用这些纸装订成50本练习本(每本用纸张数相同),每本用纸多少张?
43.如图图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)实验小学食堂用煤的天数和用煤量是否成正比例?
(2)根据图象判断,食堂5天要用煤多少吨?2.4吨煤可以用多少天?
44.某工厂有一批煤,每天烧煤的质量和可烧的时间关系如下表。
每天烧煤的质量/吨 0 3 6 9 15 20 …
可烧的时间/天 0 30 15 10 6 4.5 …
(1)判断每天烧煤的质量和可烧的时间是不是成反比例,并说明理由。
(2)如果该工厂平均每天烧煤的质量是5吨,那么这批煤可烧多少天?
45.
时间/时 1 2 3 4 5 6 …
路程/千米 90 …
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
46.王老师准备用72元钱去买笔记本.如果每本价格是2元,能买多少本?如果每本价格是3元、4元或6元呢?
每本价格/元 2 3 4 6
数量/本
观察上表,你有什么发现?
47.书房的面积是16m2,刚好用了32块地砖,卧室的面积是20m2,用同样的地砖,需要多少块?
48.四名同学到超市购买练习本,先填表,再回答问题.
(1)他们都带了6元,购买了不同品种的练习本.
张华 李浩 王佟 陈刚
单价/(元/本) 0.60 1.20 1.50 2.00
购买的数量/本
他们带的钱数相同,练习本的单价和购买的数量成什么比例?为什么?
(2)他们都买单价是0.60元/本的练习本.
张华 李浩 王佟 陈刚
购买的数量/本 2 5 8 9
用去的金额/元
购买的练习本单价相同,购买的数量和用去的金额成什么比例?为什么?
(3)已知他们买练习本用去的金额,且每人都带了6元.
张华 李浩 王佟 陈刚
用去的金额/元 0.6 1.2 1.5 2
剩下的金额/元
带的金额相同,用去的金额和剩下的金额成比例吗?为什么?
49.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数 20 15
10
需要的天数
12 15
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
50.邮局准备把一批《百科全书》打包寄给山区的小朋友。每包的本数和包数如下表。
每包的本数/本 10 20 40
包数/包 60 30 15
(1)判断每包的本数和包数是不是成反比例,并说明理由。
(2)如果打包成6包,那么每包多少本?
51.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 4 9 16
所需小正方形的数量/个 216 96 54
(1)每个小正方形的面积与所需小正方形的数量成 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
52.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
53.每5m花布售价40元.
花布长度/m 1 2 3 4 5 6 7 8
总价/元 40
①把上表填完整.
②花布总价和长度是否成正比例?为什么?
54.王叔叔要把一张100元换成小面值的人民币.
面值/元 1 2 5 10 20 50
数量/张
(1)把表填写完整.
(2)人民币面值和张数成反比例吗?为什么?
55.判断下面每题中的两种量是否成正比例关系,并说明理由.
(1)全班人数一定,出勤人数与缺勤人数;
(2)《光明日报》的单价一定,总价与数量.
56.A、B两种商品的价格之比为7:2,如果它们的价格分别上涨60元后,价格之比为5:2,这两种商品原来的价格各是多少?
57.某物流公司将一批货物运往一家加工厂,且要一次性把所有货物全部运出,车辆的载质量与所需车辆的数量如表所示。
车辆的载质量/t 2.5 3 5 10
所需车辆的数量/辆 48 40 24 12
(1)车辆的载质量和所需车辆的数量成什么比例?如果用载质量为6t的车来运,那么一共需要多少辆?
(2)如果用15辆车来运,那么每辆车要运多少吨?
58.下图表示一根水管不停地向水箱内注水时,水箱内水的体积的变化情况.
(1)水箱内水的体积与注水的时间成正比例吗?为什么?
(2)利用图象估一估,10分能注水多少升?注水45升需要多少分?再实际计算一下.
59.一个平行四边形的面积是24m2,用x和y表示它的底和高.x与y成什么比例关系?如果把它们的关系用图象表示出来,那么它的图象是一条直线吗?
60.“六一”那天,芳芳和小朋友们一起骑车去动物园玩.下面的图象表示的是她骑车的路程和时间的关系.
(1)芳芳骑车行驶的路程和时间成正比例吗?为什么?
(2)看图估计,行2.5千米大约用多少分钟?
期末专项培优 正比例和反比例
参考答案与试题解析
1.一辆汽车两次行驶的路程与耗油量如下表:
行驶路程/km 24 96
耗油量/L 2 8
(1)分别写出每次行驶路程与耗油量的比值,判断这两个比能否组成比例.
(2)分别写出两次耗油量与对应行驶路程的比值,看看这两个比能否组成比例.
【答案】见试题解答内容
【分析】(1)根据题意,先写出两次行驶路程与耗油数量的比,然后分别求出比值,通过比较比值判断出两次行驶路程与耗油数量的比能否组成比例.如果比值相等,能组成比例,反之则不能.
(2)先写出两次行驶的路程的比,与两次耗油量的比,然后分别求出比值,通过比较比值判断出两次行驶路程与耗油数量的比能否组成比例.如果比值相等,能组成比例,反之则不能.
【解答】解:(1)行驶路程与耗油数量的比分别是:
24:2
96:8
24:2=12
96:8=12
12=12
所以这两个比能组成比例.
(2)两次耗油量与对应行驶路程的比分别是:
2:24
8:96
2:24
8:96
所以这两个比能组成比例.
【点评】解答此题的关键是明确比例的判定方法,即两个比的比值相同就能组成比例,然后再进一步解答.
2.被除数一定,商和除数成 反 比例。
【答案】反比例。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:因为每班人数×班数=总人数(一定),是对应的乘积一定,所以每行人数与行数成反比例;
故答案为:反。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
3.一种硬笔书法练习本,数量和总价的关系如表.
数量/本 1 2 3 4 5 6 …
总价/元 4 8 12 16 20 24 …
(1)在图中,描出总价与数量之间的对应点,并连接各点.
(2)总价与数量有什么关系?为什么?
【答案】见试题解答内容
【分析】(1)首先根据表中的数据描出各点,然后顺次连接个点即可.
(2)因为单价(一定),所以总价和数量成正比例.
【解答】解:(1)作图如下:
(2)4
因为单价(一定),所以总价和数量成正比例.
【点评】此题考查的目的是理解掌握正比例的意义及应用,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(即两个数的商)一定,这两种就叫做成正比例的量,它们的关系就是正比例关系.
4.如图的图象表示长颈鹿的奔跑情况.
(1)长颈鹿的奔跑路程与奔跑时间成 正 比例关系.
(2)请你计算一下,长颈鹿16分钟跑多少千米?
【答案】见试题解答内容
【分析】(1)通过观察图可知,速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,据此列比例解答.
【解答】解:(1)因为速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,
5x=4×16
x
x=12.8
答:长颈鹿16分钟跑12.8千米.
故答案为:正.
【点评】此题考查的目的是理解掌握正比例的意义及应用,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(即两个数的商)一定,这两种就叫做成正比例的量,它们的关系就是正比例关系.
5.如图中线段AB表示一辆汽车行驶的路程与时间的关系.
①这辆汽车行驶了多长时间?行驶了多少千米?
②这辆汽车2.5小时行驶了多少千米?
③这辆汽车行驶900km要多长时间?
【答案】见试题解答内容
【分析】①找出这辆汽车的终点,根据图表找出对应的时间和路程.
②先根据“路程÷时间=速度”求出汽车的速度,进而根据“速度×时间=路程”进行解答即可.
③先根据“路程÷速度=时间”求出汽车行驶900km所需时间.
【解答】解:①这辆汽车的终点,根据图表找出对应的时间是3小时,路程是180千米.
答:这辆汽车行驶了3小时,行驶了180千米.
②180÷3=60(km/h),60×2.5=150(km).
答:这辆汽车2.5小时行驶了150千米.
③900÷60=15(h).
答:这辆汽车行驶900km要15小时
【点评】此题考查了学生从统计图中挖掘信息以及处理数据的能力,同时考查了正反比例的知识和对行程问题的掌握.
6.装配一批机器,每天装配的数量和需要的天数如下表。
每天装配的数量/台 40 80 100 160 200 400
需要的时间/天 40 20 16 10 8 4
(1)每天装配的数量和需要的时间成反比例关系吗?说明理由。
(2)如果每天装配64台,需要多少天装配完?
【答案】(1)每天装配的数×需的时间=总工作量(一定),所以每天装配的数量和需要的时间成反比例;(2)25天。
【分析】(1)根据表可知每天装配的数与需的时间的乘积一定,据此可的每天装配的数量和需要的时间成反比例;
(2)由(1)可知,每天装配的数量和需要的时间成反比例,用它们的乘积除以每天装配的台数即可解答。
【解答】解:(1)40×40=1600(台)
80×20=1600(台)
100×16=1600(台)……
即:每天装配的数×需的时间=总工作量(一定),所以每天装配的数量和需要的时间成反比例。
(2)40×40÷64
=1600÷64
=25(天)
答:需要25天装配完。
【点评】掌握反比例的意义是解决此题的关键。
7.一辆变速自行车,前齿轮有2个,后齿轮有6个,前齿轮的齿数分别是40和36,后齿轮的齿数分别是32、30、28、26、24、20.
(1)这辆自行车能变化出多少种不同的速度?(先填表,再解答)
(2)蹬同样的圈数,要使自行车骑得最远,前、后齿轮的齿数比应是多少?
前齿轮齿数/前、后齿轮齿数比/后齿轮齿数 40 36
32
30
28
26
24
20
【答案】见试题解答内容
【分析】(1)根据比的定义计算即可求解;
(2)根据变速自行车原理,前后齿轮数的比值越大,前齿轮转一圈,后齿轮所转的圈数就越多,所以得出前齿轮齿数最多,后齿轮齿数最少时自行车跑得最远.
【解答】解:(1)填表如下:
前齿轮齿数/前、后齿轮齿数比/后齿轮齿数 40 36
32 5:4 9:8
30 4:3 6:5
28 10:7 9:7
26 20:13 18:13
24 5:3 3:2
20 2:1 9:5
故这辆自行车能变化出12种不同的速度;
(2)蹬同样的圈数,要使自行车骑得最远,前、后齿轮的齿数比应是2:1.
【点评】主要依据变速自行车原理来组合,即前后齿轮数的比值越大,前齿轮转一圈,后齿轮所转的圈数就越多.
8.用24个边长1cm的小正方形,你能拼成几种不同的长方形?
(1)认真思考,完成表格。
长/cm
宽/cm
(2)从表中,你发现长和宽有怎样的比例关系?
【答案】
长/cm 24 12 8 6
宽/cm 1 2 3 4
反。
【分析】(1)24的因数有1,2,3,4,6,8,12,24,用24个小正方形拼成的长方形,由此进行解答;
(2)判断两个相关的量之间成什么关系,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,就成反比例,即可解答。
【解答】解:(1)根据分析知拼成后图形的面积不变,拼成后长方形的长和宽可分下列情况:
长/cm 24 12 8 6
宽/cm 1 2 3 4
所以能拼成4种不同的长方形;
(2)长方形的面积=长×宽
24×1=24(平方厘米)
12×2=24(平方厘米)
8×3=24(平方厘米)
6×4=24(平方厘米)
面积一定,就是乘积一定,长和宽成反比例关系。
【点评】本题的关键是根据拼成后面积不变,分情况讨论组成长方形的长和宽
9.四名同学都看了《少年学党史》这本书。请填写出每人看完这本书需要的天数。
郑小强 张小华 李小虹 王小新
每天看的页数 6 10 15 20
看的天数 30
18
12
9
照这样的速度看了3天,他们各看了多少页?还剩下多少页?
郑小强 张小华 李小虹 王小新
已看的页数
18
30
45
60
剩下的页数
162
150
135
120
题中,每天看的页数和看的天数 成反 比例,已看的页数和剩下的页数 不成 比例。
【答案】18,12,9;18,30,45,60;162,150,135,120;成反,不成。
【分析】(1)用郑小强每天看的页数6×看的总天数30=这本书的总页数,用总页数分别除以张小华、李小虹、王小新每天看的页数,就是他们分别看的天数;
(2)分别用郑小强、张小华、李小虹、王小新每天看的页数乘3天,就是他们3天各自看的页数,再用郑小强每天看的页数6×看的总天数30=这本书的总页数,用总页数减去他们3天各自看的页数,就是他们各自剩下的页数;判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:(1)30×6=180(页)
180÷10=18(天)
180÷15=12(天)
180÷20=9(天)
答:张小华需要看18天,李小虹需要看12天,王小新需要9天。
(2)6×3=18(页)
10×3=30(页)
15×3=45(页)
20×3=60(页)
6×30=180(页)
180﹣18=162(页)
180﹣30=150(页)
180﹣45=135(页)
180﹣60=120(页)
答:他们分别看了18页、30页、45页、60页,分别剩下162页、150页、135页、120页。
因为每天看的页数×看的天数=180(页)(一定),乘积一定,所以每天看的页数和看的天数成反比例;
已看的页数+剩下的页数=180(页)(一定),和一定,所以已看的页数和剩下的页数不成比例。
故答案为:18,12,9;18,30,45,60;162,150,135,120;成反,不成。
【点评】明确每天看的页数×看的天数=看的页数以及辨识成正、反比例的量的方法是解题的关键。
10.一列火车匀速行驶时,路程与时间的关系如表.
时间/小时 1 2 3 4 5 …
路程/千米 120 240 …
(1)完成上表.
(2)根据表格中的数据,这列火车行驶的路程与时间成什么比例?
(3)如果A、B两城相距420千米,需要多少小时可以从A城到达B城?
【答案】见试题解答内容
【分析】(1)根据路程、速度、时间三者之间的关系即可分别求出火车的路程,然后填表.
(2)根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就是成反比例的量,它们的关系是反比例关系.即形如xy=k(一定),x、y是成反比例的量,x与y成反比例关系.依此即可求解.
(3)根据时间=路程÷速度即可解答.
【解答】解:(1)120×3=360(千米)
120×4=480(千米)
120×5=600(千米)
填表如下:
时间/小时 1 2 3 4 5 …
路程/千米 120 240 360 480 600 …
(2)因为路程÷时间=速度(一定),所以这列火车行驶的路程与时间成正比例;
(3)420÷120=3.5(小时)
答:需要3.5小时可以从A城到达B城.
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
11.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量/辆 1 2 3 4 5 6 7
运货质量/吨 4 8 12 16 20 24 28
(1)表中 汽车数量 和 运货质量 是两种相关联的量, 运货质量 随着 汽车数量 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
【答案】见试题解答内容
【分析】(1)根据题意知:表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
【解答】解:(1)表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
故答案为:汽车数量;运货质量;运货质量;汽车数量.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
12.已知两个数M、N满足等式9N,数M与N成什么比例关系?请说明理由.
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为9N,
9×9×MN×9×M
所以MN=81(一定),
即对应的乘积一定;
所以数M与N成反比例关系.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
13.一辆汽车在高速公路上行驶的路程与耗油量的关系如下表:
行驶路程/km 50 100 150 200 250 …
耗油量/L 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来.
(2)这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350千米的耗油量.
(4)这辆汽车出发时油箱里有汽油40升,如果汽车要在高速公路上行驶460千米,你认为司机在途中需要加油吗?
【答案】见试题解答内容
【分析】(1)根据统计表中的数据完成统计图.
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;由此解答即可.
(3)根据耗油量=汽车行驶的路程除以每升油行驶的路程,计算即可.
(4)计算460千米需要多少升汽油,与40升进行比较,即可得出结论.
【解答】解:(1)统计图如下:
(2)50÷5=100÷10=150÷15=10(一定),即:汽车行驶的路程÷耗油量=每升油行驶的路程(一定),
所以这辆汽车行驶的路程和耗油量成正比例.
(3)350÷10=35(升)
答:这辆汽车行驶350千米的耗油量为35升.
(4)460÷10=46(升)
46>40
答:司机在途中需要加油.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
14.如图的图象反映的是购买两种练习本的数量和总价的变化情况.
(1)购买甲种练习本的数量和总价是否成正比例?乙种呢?
(2)估计一下,买5本甲种练习本多少元?2.8元可以买几本甲种练习本?
(3)从图上看哪种练习本便宜些?2.4元可以买两种练习本各多少本?
【答案】见试题解答内容
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
(2)估计买5本甲种练习本的价钱,先找到甲图象与数量5的交点,看看这个交点对应的数轴的数值即可解答,估计2.8元可以买几本甲种练习本,看2.8元与甲图象的交点所对应的数值.
(3)看1本对应的单价即可解答.先根据图象求两种练习本的单价,根据单价求2.4元买两种练习本的本数.
【解答】解:(1)甲:0.4÷1=0.8÷2=1.2÷3=0.4,即总价÷数量=单价(一定),所以甲种练习本的数量和总价成正比例;
乙:0.4÷2=0.8÷4=1.2÷6=0.2,即总价÷数量=单价(一定),所以乙种练习本的数量和总价成正比例.
(2)5本甲种练习本对应的价钱大约是2元
2.8元与甲种练习本对应的数量是7
答:5本乙种练习本的价钱是1元,2.8元可以买,7本甲种练习本.
(3)从图上看,1本书对应的本数的乙的单价低,所以乙种练习本便宜些.
3.2÷8=0.4(元/本)
2.4÷12=0.2(元/本)
2.4÷0.4=6(本)
2.4÷0.2=12(本)
答:乙种练习本便宜.2.4元可以买6本甲或12本乙练习本.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
15.兰兰坐爸爸开的车去看爷爷,她每过10分钟看一次里程表上的读数,结果如下:
时间 9:10 9:20 9:30 9:40 9:50 …
里程表读数/km| 31220 31235 31250 31265 31280 …
(1)这辆汽车行驶的路程和时间之间有什么关系?它们成正比例关系吗?为什么?
(2)如果9:50时离爷爷家还有45千米,照这样的速度,他们在什么时刻可以到达爷爷家?
【答案】见试题解答内容
【分析】(1)后面一个里程表读数减相邻的前一个里程表读数就是此时间段所行驶的路程.据此即可分别求出各时间段所行驶的路程.根据时间的推算,用后一个时刻减前一个相邻时刻就是此时间段的时间.通过计算可以发现时间段相同,所行驶的路程也相同.根据“速度=路程÷时间”,计算出这辆汽车的速度,如果速度相等,即一定,即路程÷时间=速度(一定),则路程与时间成正比例关系.
(2)根据“时间=路程÷速度”求出45千克路程所需要的时间,用9时50分加所用的时间就是到家的时刻.
【解答】解:(1)9时20分﹣9时10分=10分
31235﹣31220=15(km)
15÷10=1.5(km/分);
9时30分﹣9时20分=10分
31250﹣31235=15(km)
15÷10=1.5(km/分);
9时40分﹣9时30分=10分
31265﹣31250=15(km)
15÷10=1.5(km/分);
9时50分﹣9时40分=10分
31280﹣31265=15(km)
15÷10=1.5(km/分);
……
这辆汽车行驶的路程和所用时间的比值(商)一定,它们成正比例关系.
理由:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量,它们的关系是正比例关系.
(2)45÷1.5=30(分)
9时50分+30分=10时20分
10时20分即10:20
答:他们在10:20可以到达爷爷家.
【点评】此题主要是考查了两个方面的内容:正、反比例的辨析;时间的推算.
16.认真观察图像,回答问题。
(1)图像中这两种量成正比例关系吗?为什么?
(2)根据所列出的两种量的关系。完成下表。
x 1 2.5 15
y 200
【答案】(1)成正比例关系。
(2)20,50,10,300。
【分析】(1)正比例图像是一条直线,反比例图像是一条平滑的曲线。
(2)根据比值一定,求出对应的值,填入表中。
【解答】解:(1)图像是一条直线,所以两种量成正比例关系。
(2)
x 1 2.5 10 15
y 20 50 200 300
【点评】本题考查正比例图像的判断及根据图像解决问题,根据是根据图像分析数量关系。
17.(1)分别写出图中两个长方形长与长的比和宽与宽的比,并求比值,然后判断这两个比能否组成比例,若能组成比例,请把这个比例写出来.
(2)分别写出图中每个长方形长与宽的比,并求比值,然后判断这两个比能否组成比例,若能组成比例,请把这个比例写出来.
【答案】见试题解答内容
【分析】(1)先求得两个长方形长与长的比和宽与宽的比,进而化简比,并求比值,根据比例的意义判断能否组成比例,再把这个比例写出来即可.
(2)先求得每个长方形长与宽的比,进而化简比,并求比值,根据比例的意义判断能否组成比例,再把这个比例写出来即可.
【解答】解:(1)两个长方形长与长的比是2.5:1.5=5:3
两个长方形宽与宽的比是2:1.2=5:3
,
所以这两个长方形长与长的比和宽与宽的比能组成比例,为2.5:1.5=2:1.2.
(2)大长方形的长与宽之比是2.5:2=5:4
小长方形的长与宽之比是1.5:1.2=5:4
,
所以这两个长方形的长与宽之比能组成比例,为2.5:2=1.5:1.2.
【点评】此题考查用比例的性质辨识两个比能否组成比例,关键是看这两个比的比值是否相等,比值相等,就能组成比例,比值不相等,就不能组成比例.
18.一种花布的数量和总价如表.
数量/m 1 2 3 4 5 6 7 ……
总价/元 8 16 24 32 40 48 56 ……
(1)表中的总价和数量成正比例关系吗?为什么?
(2)在如图中描出表示数量和对应总价的点,然后把它们连起来,并说说图象的特点.
(3)利用图象回答,买2.5m花布需要多少元?68元能买多少米花布?
【答案】见试题解答内容
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示k(一定).
(1)通过计算总价与数量的比值是否一定,来判定总价与数量是否成正比例关系即可.
(2)描点,连线即可.
(3)利用图象看2.5m所对应的图象上的点所对应的总价是多少元即可,然后再看68元所对应的图象上的点所对应的数量是多少米即可.
【解答】解:(1)总价和数量成正比例关系.
因为8(一定),是比值一定,
所以总价和数量成正比例关系.
(2)
由图可知正比例关系的图象是一条射线.
(3)根据图象可知:买2.5m花布需要20元,68元能买米8.5米花布.
【点评】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值.还要学会利用数形结合的思想解决数学问题.
19.妈妈带的钱可以买单价为30元的猪肉6kg或单价为60元的牛肉3kg。
(1)妈妈一共带了多少钱?
(2)如果买单价为72元的羊肉,可以买多少千克?
(3)总价一定时,单价和数量成什么比例?用等式表示出它们的关系。
【答案】(1)180,(2)2.5,(3)反比例,单价×数量=总价(一定)。
【分析】(1)根据单价×数量=总价,列式解答即可;
(2)根据总价÷单价=数量,列式解答即可;
(3)总价一定时,看单价和数量是商一定还是积一定,如果是商一定就成正比例,如果是积一定则成反比例。
【解答】解:(1)30×6=180(元)
答:妈妈一共带了180元钱。
(2)180÷72=2.5(千克)
答:可以买2.5千克。
(3)单价×数量=总价(一定),所以总价一定时,单价和数量成反比例。
【点评】熟练掌握单价、数量、总价之间的关系以及辨识成正比例和反比例的量是解决此题的关键。
20.一艘轮船从甲港开到乙港,3时行驶了75km.从乙港开到丙港,5时行驶了125km.
(1)分别求轮船从甲港开到乙港,从乙港开到丙港的速度.
(2)轮船行驶的路程和所用时间成什么比例?
(3)用等式把题目里的数量关系表示出来.
【答案】见试题解答内容
【分析】(1)知道从甲港开到乙港的路程是75km,时间是3小时,利用“速度=路程÷时间”可求得从甲港开到乙港的速度; 同理可求得从乙港开到丙港的速度.
(2)由(1)可知速度(一定),可知行驶的路程和所用时间之间的关系.
(3)根据(2)中所成的比例关系表示出来即可.
【解答】解:从甲港开到乙港的速度:75÷3=25(千米/时).
从乙港开到丙港的速度:125÷5=25(千米/时).
答:轮船从甲港开到乙港,从乙港开到丙港的速度都是25千米/时.
(2)由(1)可知25(一定),是比值一定,所以轮船行驶的路程和所用时间成正比例.
(3)设s表示路程,t表示时间,v表示速度,则等量关系为:v.
【点评】此题考查成正比例的量的应用,理解速度,时间,路程之间的关系和正比例关系的意义是解题的关键.
21.明明家的鱼缸有A,B两根进水管,先打开A管,中途打开B管。如图表示从开始加水到蓄满水的进水时间和鱼缸中水的体积的关系。
(1)从0分到6分,鱼缸中水的体积和进水时间成比例吗?如果成,成什么比例?如果不成比例,理由是什么?
(2)A管每分进水多少升?B管呢?
【答案】(1)成比例,成正比例;
(2)A管每分进水1.2升,B管每分进水1.6升。
【分析】(1)从0分到6分,鱼缸中水的体积和进水时间的比值不变,所以鱼缸中水的体积和进水时间成比例,据此解答即可;
(2)从0分到6分只有A管进水,可求出A管每分进水多少升,从6分到12分A、B管同时进水,后6分钟的用进水量减去这段时间A管的进水量,就是这段时间B管的进水量,由此即可求出B管每分进水多少升。
【解答】解:(1)从0分到6分,鱼缸中水的体积和进水时间的比值不变,鱼缸中水的体积和进水时间成比例,成正比例。
(2)A管:7.2÷6=1.2(升)
B管:(24﹣7.2)÷(12﹣6)﹣1.2
=16.8÷6﹣1.2
=2.8﹣1.2
=1.6(升)
答:A管每分进水1.2升,B管每分进水1.6升。
【点评】熟练掌握正比例和反比例的判定方法,是解答此题的关键。
22.如图的图象反映的是老虎和狮子的食肉情况.
(1)老虎的食肉量与时间成正比例吗?狮子呢?
(2)估计一下,老虎和狮子8天各食肉多少千克?
(3)哪种动物每天的食肉量较少?
【答案】见试题解答内容
【分析】(1)老虎的食肉量与所用时间的比是:10:2.4=50:12=25:6(一定);所以老虎的食肉量与所用时间成正比例.狮子的食肉量与所用时间的比是:80:12=40:6=20:3(一定);所以狮子的食肉量与所用时间成正比例.
(2)过横轴上表示8天的点作纵轴的平行线与表示老虎食肉量与天数的直线相交,过交点作横轴的平行线,与纵轴的交点处的食肉量即表示老虎8天吃肉的千克数;同理,过横轴上表示8天的点作纵轴的平行线与表示狮子食肉量与天数的直线相交,过交点作横轴的平行线,与纵轴的交点处的食肉量即表示狮子8天吃肉的千克数.
(3)根据(2)计算出老虎、狮子每天的食肉量,通过比较即可得知.
【解答】解:(1)答:老虎的食肉量与所用时间是成正比例;狮子的食肉量与所用时间是成正比例.
(2)如图
答:老虎9天可以吃约36千克肉,狮子9天吃约60千克肉.
(3)33÷8≈4(千克)
53÷8≈6(千克)
6>4
答:狮子每天的食肉量多.
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.从图象也可以判断:表示正比例关系的图形是一直线,表示反比例关系的图象是曲线
23.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是 10 元.
②12瓶的总价是 24 元.
③ 18 瓶的总价是36元.
【答案】见试题解答内容
【分析】①仔细观察图表,5瓶的售价是10元;
②先利用所给的数据求出一瓶矿泉水的价格,再根据总价=单价×数量解答即可;
③先利用所给的数据求出一瓶矿泉水的价格,用数量=总价÷单价解答即可.
【解答】解:(1)5瓶的售价是10元.
(2)10÷5×12
=2×12
=24(元);
答:12瓶的售价是 24元.
(3)36÷(10÷5)
=36÷2
=18(瓶);
答:18瓶的售价是36元.
故答案为:10,24,18.
【点评】此题主要考查正比例的意义在生活实际中的灵活应用.
24.某物流公司要将一批货物运往加工厂,如果要一次把这些货物全部运走,货车的载质量与所需车辆的数量如下表。
载质量/吨 2.5 3 5
数量/辆 48 40 24
(1)货车的载质量与所需车辆的数量成反比例吗?为什么?
(2)如果用载质量为4.8吨的货车来运,一共需要多少辆?
【答案】(1)成反比例。理由是货车的载质量与所需车辆的数量的乘积一定。
(2)25辆。
【分析】(1)2.5×48=4×30=5×24=120,得出:车辆的载重量×所需车辆的数量=总重量,则车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例。
(2)设一共需要x辆卡车。因为车辆的载重量×所需车辆的数量=总重量(一定),所以4.8乘x的积等于2.5×48的积,据此即可解答。
【解答】解:(1)2.5×48=120(吨)
3×40=120(吨)
5×24=120(吨)
因为2.5×48=3×40=5×24=120(一定),也就是货车的载质量与所需车辆的数量的乘积一定,因此货车的载质量与所需车辆的数量成反比例。
答:成反比例。理由是货车的载质量与所需车辆的数量的乘积一定。
(2)3×40÷4.8
=120÷4.8
=25(辆)
答:一共需要25辆。
【点评】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题.同时考查了学生理解分析问题的能力。
25.如图表示某工厂中甲、乙两个车间加工的零件数与时间的关系.
(1)乙车间生产的零件数与时间成正比例吗?为什么?
(2)如果生产8万个零件,那么乙车间比甲车间少用几个月?
【答案】见试题解答内容
【分析】(1)判断生产的零件数与时间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;
(2)根据工作总量÷工效=工作时间,先分别求出甲、乙车间用的时间,再相减即可.
【解答】解:(1)由图意可知,2:1=2,4:2=2,6:3=2,8:4=2…,16:8=2,
工效是一定的,工作总量和工作时间的比值一定,所以乙车间生产的零件数与时间成正比例.
(2)乙生产8万个零件需要:8÷2=4(个月)
甲生产8万个零件需要:8÷(2÷2)=8(个月)
8﹣4=4(个月)
答:如果生产8万个零件,那么乙车间比甲车间少用4个月.
【点评】本题考查了比例的有关知识,解题的关键是从折线统计图中得到进一步解题的相关信息.
26.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/cm2 900 1800 3600
所需地砖的数量/块 600 300 150
(1)所需地砖数量与每块地砖的面积成 反 比例关系。
(2)如果采用边长为50cm的方砖铺这间教室,需要多少块方砖?(用比例的方法解答)
【答案】(1)反;(2)216。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)先求出边长为50cm的方砖的面积,根据所需地砖数量与每块地砖的面积成反比例关系,设需要x块方砖,根据题意列出比例式,解答即可。
【解答】解:(1)900×600=540000(cm )
1800×300=540000(cm )
3600×150=540000(cm )
即所需地砖数量×每块地砖的面积=教室的面积(一定),乘积一定,所以所需地砖数量与每块地砖的面积成反比例。
(2)设需要x块方砖。
50×50x=540000
2500x=540000
x=216
答:需要216块这样的方砖。
故答案为:反。
【点评】熟练掌握判断两个相关联的量之间成什么比例的方法以及应用反比例关系解决实际问题的方法是解题的关键。
27.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t 2.5 3 5 10
数量/辆 48 40
24
12
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
【答案】见试题解答内容
【分析】2.5×48=3×40=120,得出:运用车辆的载重量×所需车辆的数量=总重量,则用总重量分别除以5,10求出各用的辆数.填写统计表.
(1)由统计表中的数量可以看出,车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例.
(2)运用总重量除以6就是运用卡车的辆数.
(3)运用总重量除以卡车的量数15就是每辆卡车运多少吨.
【解答】解:3×40÷5
=120÷5
=24(辆)
3×40÷10
=120÷10
=12(辆)
载质量/t 2.5 3 5 10
数量/辆 48 40 24 12
(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,
所以车辆的载重量与所需车辆的数量成反比例.
(2)120÷6=20(辆)
答:用载重量6吨的卡车来运,一共需要20辆.
(3)120÷15=8(吨)
答:每辆卡车运8吨.
故答案为:24;12.
【点评】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题.同时考查了学生理解分析问题的能力.
28.下面是某学校一个漏水的水龙头的滴水情况统计表。
滴水量/mL 20 40 60 80 100 ……
时间/分 1 2 3 4 5 ……
(1)滴水量和时间成 正 比例。
(2)这个水龙头每时滴水多少升?
(3)如果用一个底面积是10dm2,高是3dm的圆柱形水桶接漏的水,那么多长时间能接满?(水桶的厚度忽略不计)
【答案】(1)正;(2)1.2升;(3)1500分钟。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)用每分钟的滴水量乘1小时,就是这个水龙头每时的滴水量;
(3)根据圆柱的体积=底面积×高,代入数据求出圆柱形水桶的体积,再除以每分钟的滴水量即可解答。
【解答】解:(1)因为20÷1=20(mL)
40÷2=20(mL)
60÷3=20(mL)
……
滴水量÷时间=20(mL)(一定),商一定,所以滴水量和时间成正比例。
(2)1小时=60分钟
20×60=1200(mL)
1200mL=1.2L
答:这个水龙头每时滴水1.2升。
(3)20毫升=0.02升=0.02立方分米
10×3÷0.02
=30÷0.02
=1500(分钟)
答:1500分钟能接满。
故答案为:正。
【点评】本题考查了判断两个相关联的量之间成什么比例的方法、工作量、工作效率、工作时间的关系以及圆柱体积的计算方法。
29.判断下列各题中的两个量是否成比例关系.若成,成什么比例关系?
(1)每小时加工零件数一定,加工时间和加工零件总数. 成正比例
(2)从甲地去乙地,已行的路程和未行的路程. 不成比例
(3)圆的直径和周长. 成正比例
(4)已知x(y≠0),x和y. 成反比例
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:(1)加工零件总数÷加工时间=每小时加工零件数(一定),是比值一定,所以加工的时间和加工零件总数成正比例;
(2)已行的路程+未行的路程=总路程(一定),是和一定,所以已行的路程和未行的路程不成比例;
(3)圆的周长÷直径=圆周率(一定),是比值一定,所以圆的直径和周长成正比例.
(4)因为x(y≠0),所以xy=3(一定)是乘积一定,符合反比例的意义,所以x与y成反比例.
故答案为:成正比例,不成比例,成正比例,成反比例.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
30.下面的图象表示小强从甲地到乙地不同的速度和所对应的时间。
(1)在这个过程中,哪种量没有变?
(2)速度和所对应的时间成什么比例关系?
(3)不计算,观察图象,如果每小时行40km,那么从甲地到乙地大约需要多少小时?
【答案】见试题解答内容
【分析】(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化。
(2)观察图象发现速度和时间的关系是反比例关系。
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时。
【解答】解:(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化。
(2)观察图象发现速度和时间的关系是反比例关系。
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时。
【点评】此题主要考查反比例的意义。解题的关键是掌握反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
31.如图,甲、乙两车运货的吨数与次数的关系如图.
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
【答案】见试题解答内容
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示k(一定).成正比例关系的图象是经过原点的一条直线.
(1)根据图中数据,算一算甲、乙中两种变量之间的比值是否一定即可.
(2)先求出1次甲比乙多运多少,再求出6次甲比乙多运多少即可.
【解答】解:(1)甲:6(一定),是比值一定,所以甲车的运货量与运货次数成正比例关系.
乙:4(一定),是比值一定,所以乙车的运货量与运货次数成正比例关系.
(2)18÷3﹣12÷3
=6﹣4
=2(吨)
2×6=12(吨)
答:甲、乙两车各运货6次,运货量相差12吨.
【点评】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值.并且知道正比例关系的图象是经过原点的一条射线.
32.判断下面各题中的两种量是否成比例?成什么比例?为什么?
(1)小麦的出粉率一定,小麦的总重量和出粉的重量。
(2)每箱木瓜的个数一定,运来木瓜的箱数和木瓜的总个数。
(3)房间的面积一定,铺地砖的块数与每块地砖的面积。
【答案】(1)成正比例,因为出粉的重量与小麦的重量的商一定;
(2)成正比例,因为木瓜的总个数与运来木瓜的箱数的商一定;
(3)成反比例,因为铺地砖的块数与每块地砖的面积的乘积一定。
【分析】两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例。据此判断。
【解答】解:(1)小麦的出粉率=出粉的重量÷小麦的重量×100%,小麦的出粉率一定时,小麦的总重量和出粉的重量成正比例;
(2)木瓜的总个数÷运来木瓜的箱数=每箱木瓜的个数,每箱木瓜的个数一定时,运来木瓜的箱数和木瓜的总个数成正比例;
(3)房间的面积=铺地砖的块数×每块地砖的面积,房间的面积一定时,铺地砖的块数与每块地砖的面积成反比例。
【点评】辨识两种相关联的量成正比例还是成反比例,就看这两种量的比值一定还是乘积一定。
33.把相同体积的水倒入底面积不同的杯子.
水的高度/cm 30 20 15 10 5 …
杯子的底面积/cm2 10 15 20 30 60 …
水的高度和杯子的底面积成反比例吗?为什么?
【答案】见试题解答内容
【分析】根据水的体积=杯子的底面积×水面的高度,列式计算,通过计算可得:水的体积一定,也就是水的高度和杯子的底面积的乘积一定,所以杯子的底面积和水的高度是成反比例的量,据此即可得解.
【解答】解:水的高度和杯子的底面积成反比例.
因为30×10=300(立方厘米)
20×15=300(立方厘米)
15×20=300(立方厘米)
10×30=300(立方厘米)
5×60=300(立方厘米)
通过计算可得:水的体积一定,也就是水的高度和杯子的底面积的乘积一定,所以杯子的底面积和水的高度成反比例.
【点评】此题主要考查反比例的意义和圆柱的体积公式的灵活应用.
34.配制一种盐水,水的质量总是比盐水的质量少15%,盐的质量与盐水的质量成正比例吗?
【答案】成正比例。
【分析】判断两种量成正比例还是成反比例时,关键看这两种相关联的量中相对应的两个数是比值一定还是乘积一定。如果比值一定,就成正比例;如果乘积一定,就成反比例;如果比值和乘积都不是定量,就不成比例。
【解答】解:(盐水的质量﹣水的质量)÷盐水的质量=盐的质量÷盐水的质量=15%,盐的质量与盐水的质量是两个相关联的量,且它们的比值一定,所以成正比例。
【点评】此题考查了辨识成正比例的量与成反比例的量,要求学生掌握。
35.某厂要生产一批豆浆机,平均每天产量和所需时间如表。
平均每天产量/台 200 300 500
所需时间/天 75 50 30
(1)平均每天产量和所需时间成 反 比例。
(2)现要在20天内完成生产任务,平均每天产量至少要达到多少台?
【答案】(1)反;(2)750。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)因为平均每天产量和所需时间成反比例,总台数不变,用总台数除以需要的天数即可解答。
【解答】解:(1)因为200×75=15000
300×50=15000
500×30=15000
所以平均每天产量×所需时间=15000(一定),乘积一定,所以平均每天产量和所需时间成反比例;
(2)15000÷20=750(台)
答:平均每天产量至少要达到750台。
故答案为:反。
【点评】熟练掌握判断两个相关联的量之间成什么比例的方法以及求平均数的方法是解题的关键。
36.妈妈买来一袋橡皮泥,平平全部用来捏大小相同的圆锥,正好没有剩余.圆锥的个数与每个圆锥所用橡皮泥的体积是否成反比例?为什么?
【答案】见试题解答内容
【分析】由于所捏的圆锥的大小相同,因此,每个圆锥所用的橡皮泥是相同的.每个圆锥用的橡皮泥×圆锥的个数=妈妈买来一袋橡皮泥(一定).根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就是成反比例的量,它们的关系是反比例关系,在这里,每个圆锥用的橡皮泥×圆锥的个数成反比例.
【解答】解:圆锥的个数与每个圆锥所用橡皮泥的体积是成反比例
理由:每个圆锥用的橡皮泥×圆锥的个数=妈妈买来一袋橡皮泥(一定)
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
37.某童车厂装配一批童车,每天装配的数量和需要的时间如表。
每天装配的数量/辆 60 90 120 180 360 …
时间/天 60 40 30 20 10 …
(1)判断每天装配的数量和时间是否成反比例,并说明理由。
(2)如果每天装配200辆,多少天可以装配完这批童车?
【答案】(1)成反比例;因为60×60=90×40=120×30=180×20=360×10=定值,所以每天装配的数量和时间成反比例;
(2)18天。
【分析】两个相关联的量的乘积不变时,这两个量成反比例关系,据此解答即可。
【解答】解:(1)每天装配的数量和时间成反比例。
因为60×60=90×40=120×30=180×20=360×10=定值,所以每天装配的数量和时间成反比例。
(2)60×60÷200
=3600÷200
=18(天)
答:如果每天装配200辆,18天可以装配完这批童车。
【点评】熟练掌握反比例关系的判断,是解答此题的关键。
38.科技小组制作了一个弹簧秤,弹簧的长度是8厘米。经验证,弹簧的长度与所挂钩码的质量存在如下关系:
弹簧长度/cm 8 9 10 11 ……
钩码质量/kg 0 2 4 6 ……
(1)钩码的质量和弹簧伸长的长度成什么比例关系?
(2)小亮用科技小组制作的这个弹簧秤称一个物体,弹簧的长度是14.8cm,这个物体的质量是多少千克?(用比例知识解答)
【答案】(1)正比例关系;(2)13.6千克。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
(2)设这个物体的质量是x千克,由(1)可知,弹簧伸长的长度与钩码的质量成正比例关系,据此用弹簧的长度减去弹簧原来的长度与x的比等于0.5,据此列式解答即可。
【解答】解:(1)当弹簧的长度是8厘米时,钩码质量是0kg;
当弹簧的长度是9厘米时,钩码质量是2kg,即弹簧伸长(9﹣8)厘米;
当弹簧的长度是10厘米时,钩码质量是4kg,即弹簧伸长(10﹣8)厘米;
当弹簧的长度是11厘米时,钩码质量是6kg,即弹簧伸长(11﹣8)厘米;
......
(9﹣8):2=0.5
(10﹣8):4=0.5
(11﹣8):6=0.5
......
弹簧伸长的长度:钩码的质量=0.5(一定),商一定,所以钩码的质量和弹簧伸长的长度成正比例关系。
(2)设这个物体的质量是x千克。
(14.8﹣8):x=0.5
0.5x=6.8
x=13.6
答:这个物体的质量是13.6千克。
【点评】熟练掌握判断两个相关联的量之间成什么比例的方法以及利用正比例解题的方法是解题的关键。
39.判断下面每题中的两种量是不是成正比例,并说明理由.
(1)小新跳高的高度和他的身高.
(2)长方形的宽一定,它的面积和长.
(3)小麦每公顷产量一定,小麦的公顷数和总产量.
【答案】见试题解答内容
【分析】判定两种量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定,就成反比例.
【解答】解:(1)因为小新跳高的高度和他的身高的比值不是一定的,
所以小新跳高的高度和他的身高不成正比例;
(2)因为长方形的面积=长×宽,
所以长方形的面积÷长=宽(一定),
即长方形的面积与长的比值一定,
符合正比例的意义,
所以一个长方形的宽一定,它的面积和长成正比例;
(3)种小麦的面积和总产量是两种相关联的量,它们与每公顷小麦产量有下面的关系:
总产量:小麦的公顷数=每公顷小麦产量(一定);
已知每公顷小麦产量一定,也就是总产量与种小麦的公顷数的比值一定,所以种小麦的公顷数和总产量成正比例.
【点评】此题属于根据正、反比例的意义,判断两种相关联的成正比例还是成反比例,就看是对应的比值一定,还是对应的乘积一定,再做出解答.
40.小牛和大牛吃肥肉,原来小牛和大牛吃的肉块数之比为2:5,后来小牛又吃了5块,大牛也又吃了2块,此时小牛和大牛吃的肉块数之比为5:9,求原来两人各自吃了多少块肥肉?
【答案】小牛原来吃10块,大牛原来吃25块。
【分析】设原来小牛吃了2x块肥肉,大牛吃5x块肥肉,根据等量关系:(原来小牛吃的块数+5块):(原来大牛吃的块数+2块)=5:9,列方程解答即可。
【解答】解:设原来小牛吃了2x块肥肉,大牛吃5x块肥肉
(2x+5):(5x+2)=5:9
25x+10=18x+45
x=5
5×2=10(块)
5×5=25(块)
答:小牛原来吃10块,大牛原来吃25块。
【点评】本题主要考查了比例的应用,关键是根据等量关系:(原来小牛吃的块数+5块):(原来大牛吃的块数+2块)=5:9。
41.新冠肺炎疫情期间,口罩需求量大幅上升。某工厂接到任务紧急生产一批口罩,下面是每时生产口罩的数量与完成任务总共需要的时间的关系。
每时生产口罩的数量/万只 2 3 4 6
时间/时 72 48 36 24
(1)每时生产口罩的数量与时间有什么关系?(1分)
(2)如果每时生产8万只口罩,那么完成这项任务一共需要多少时?(4分)
【答案】(1)反比例;
(2)18。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:(1)因为每时生产口罩的数量与时间的积一定,所以每时生产口罩的数量与时间成反比例。
(2)2×72÷8=18(时)
答:完成这项任务一共需要18小时。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
42.用一些纸装订同样的练习本,每本用纸的张数和装订的本数如表。
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40
30
25
(1)将如表补充完整。
(2)每本用纸张数和装订本数是否成反比例关系?为什么?
(3)如果用这些纸装订成50本练习本(每本用纸张数相同),每本用纸多少张?
【答案】(1)30;25;
(2)因为8×75=10×60=15×40=20×30=24×25=定值,所以每本用纸张数和装订本数成反比例关系;
(3)12张。
【分析】(1)根据积都是600,用600除以20和24即可;
(2)判断练习本每本的页数和装订的本数之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
(3)用600除以50即可。
【解答】解:(1)
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40 30 25
(2)因为8×75=10×60=15×40=20×30=24×25=定值,所以每本用纸张数和装订本数成反比例关系。
(3)10×60÷50
=600÷50
=12(张)
答:每本用纸12张。
故答案为:30;25。
【点评】根据反比例的定义进行判断即可。
43.如图图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)实验小学食堂用煤的天数和用煤量是否成正比例?
(2)根据图象判断,食堂5天要用煤多少吨?2.4吨煤可以用多少天?
【答案】见试题解答内容
【分析】(1)用煤的天数和用量是两个相关联的量,用总煤量除以用煤天数就是每天的用煤量,即用煤总量÷用煤天数=每天用煤量.如果每天的用煤量一定,煤的天数和用煤量成正比例.
(2)表示5天的纵与表示用煤量的直线的交点即表示5天的用煤量,即1.5吨;表示用煤量2.4吨的横轴与表示用煤量的直线的交点即表示用煤的天数,即2.4吨煤可以有8天.
【解答】解:(1)0.3÷1=0.3(吨)
0.6÷2=0.3(吨)
0.9÷3=0.3(吨)
……
每天的用煤量一定
即用煤总量÷用煤天数=每天用煤量(一定)
答:实验小学食堂用煤的天数和用煤量成正比例.
(2)答:食堂5天要用煤1.5吨,2.4吨煤可以用8天.
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
44.某工厂有一批煤,每天烧煤的质量和可烧的时间关系如下表。
每天烧煤的质量/吨 0 3 6 9 15 20 …
可烧的时间/天 0 30 15 10 6 4.5 …
(1)判断每天烧煤的质量和可烧的时间是不是成反比例,并说明理由。
(2)如果该工厂平均每天烧煤的质量是5吨,那么这批煤可烧多少天?
【答案】(1)3×30=6×15=9×10=15×6=20×4.5=90
每天烧煤的质量和可烧的时间的乘积一定,所以每天烧煤的质量和可烧的时间成反比例。
(2)18天。
【分析】(1)根据每天烧煤的质量和可烧的时间的乘积判断。
(2)用这批煤的总质量除以每天烧煤的质量就是烧的天数。
【解答】解:(1)3×30=6×15=9×10=15×6=20×4.5=90
每天烧煤的质量和可烧的时间的乘积一定,所以每天烧煤的质量和可烧的时间成反比例。
(2)30×3÷5=18(天)
答:这批煤可烧18天。
【点评】本题考查了成反比例关系的判定及根据成反比例关系解决问题,关键是对题目中数量关系的分析。
45.
时间/时 1 2 3 4 5 6 …
路程/千米 90 …
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 正 比例,理由是 路程÷时间=速度(一定) .
③利用图象估计一下,2.5时行 225 千米,行675千米需要 7.5 小时.
【答案】见试题解答内容
【分析】①1小时行驶90千米,2小时行驶2个90千米,即180千米;3小时行3个90千米,即270千米;4小时行4个90千米,即360千米;5小时行5个90千米,即450千米;6小时行6个90千米,即540千米……然后填表,并在图中描出时间与路程对应的点,并这些点按顺序连起来.
②在这里速度一定,根据路程、速度、时间三者之间的关系,路程÷时间=速度(一定),再根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量,由此即可判定时间和路程成正比例.
③根据表示时间、路程的拆线统计图即可估计2.5小时所行的路程、行675千米年需要的时间.
【解答】解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时 1 2 3 4 5 6 …
路程/千米 90 180 270 360 450 540 …
②时间和路程成 正比例,理由是 路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行 225千米,行675千米需要 7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
【点评】此主要是考查正、反比例的辨别,关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
46.王老师准备用72元钱去买笔记本.如果每本价格是2元,能买多少本?如果每本价格是3元、4元或6元呢?
每本价格/元 2 3 4 6
数量/本 36
24
18
12
观察上表,你有什么发现?
【答案】见试题解答内容
【分析】根据数量=总价÷单价,分别用72元除以2元、3元、4元和6元求出可以购买的本数,填入表格,再根据总价一定,单价与数量的乘积一定,它们乘反比例关系求解即可.
【解答】解:72÷2=36(本)
72÷3=24(本)
72÷4=18(本)
72÷6=12(本)
表格如下:
每本价格/元 2 3 4 6
数量/本 36 24 18 12
观察上表发现:
2×36=3×24=4×18=6×12=72
即单价×数量=总价(一定),单价和数量成反比例关系.
【点评】本题考查了总价、数量和单价之间的关系,同时考查了根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择.
47.书房的面积是16m2,刚好用了32块地砖,卧室的面积是20m2,用同样的地砖,需要多少块?
【答案】40块。
【分析】根据题意知道,地砖的面积一定,房子的面积÷地砖的块数=地砖的面积(一定),所以房子的面积与方砖的块数成正比例,由此列出比例解答即可。
【解答】解:设用同样的地砖,需要X块。
16:32=20:X
16X=640
X=40
答:用同样的地砖,需要40块。
【点评】关键是判断出房子的面积与方砖的块数成正比例,由此解决问题。
48.四名同学到超市购买练习本,先填表,再回答问题.
(1)他们都带了6元,购买了不同品种的练习本.
张华 李浩 王佟 陈刚
单价/(元/本) 0.60 1.20 1.50 2.00
购买的数量/本
10
5
4
3
他们带的钱数相同,练习本的单价和购买的数量成什么比例?为什么?
(2)他们都买单价是0.60元/本的练习本.
张华 李浩 王佟 陈刚
购买的数量/本 2 5 8 9
用去的金额/元
1.2
3
4.8
5.4
购买的练习本单价相同,购买的数量和用去的金额成什么比例?为什么?
(3)已知他们买练习本用去的金额,且每人都带了6元.
张华 李浩 王佟 陈刚
用去的金额/元 0.6 1.2 1.5 2
剩下的金额/元
5.4
4.8
4.5
4
带的金额相同,用去的金额和剩下的金额成比例吗?为什么?
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:(1)他们都带了6元,购买了不同品种的练习本.
张华 李浩 王佟 陈刚
单价/(元/本) 0.60 1.20 1.50 2.00
购买的数量/本 10 5 4 3
因为练习本的单价×购买的数量=总价(一定),即乘积一定,所以练习本的单价和购买的数量成反比例.
(2)他们都买单价是0.60元/本的练习本
张华 李浩 王佟 陈刚
购买的数量/本 2 5 8 9
用去的金额/元 1.2 3 4.8 5.4
因为,总价÷购买的数量=练习本单价(一定),即商一定,所以购买的数量和用去的金额成正比例.
(3)已知他们买练习本用去的金额,且每人都带了6元.
张华 李浩 王佟 陈刚
用去的金额/元 0.6 1.2 1.5 2
剩下的金额/元 5.4 4.8 4.5 4
因为用去的金额+剩下的金额=总价,和一定.所以用去的金额和剩下的金额不成比例.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
49.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数 20 15
12
10
需要的天数
9
12 15
18
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
【答案】见试题解答内容
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系.用字母表示是k(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系.用字母表示是x×y=k(一定).
(1)这一批电动车的数量是个定值12×15=180辆,也就是:每天组装辆数×需要的天数=180辆,据此计算填表即可.
(2)根据每天组装辆数×需要的天数=180辆(一定)可解答.
(3)根据需要的天数=180÷每天组装辆数;每天组装辆数=180÷需要的天数即可.
【解答】解:(1)15×12=180(辆)
180÷20=9(天)
180÷15=12(辆)
180÷10=18(天)
每天组装辆数 20 15 12 10
需要的天数 9 12 15 18
(2)因为每天组装辆数×需要的天数=180辆(一定),即乘积一定.所以每天组装的辆数和需要的天数成反比例.
(3)180÷30=6(天)
180÷4=45(辆)
答:每天组装30辆,需要组装6天;打算4天完成组装任务,每天需要组装45辆.
故答案为:12,9,18.
【点评】此题主要考查成反比例的量,理解成反比例的量的定义,是解决此题的关键.
50.邮局准备把一批《百科全书》打包寄给山区的小朋友。每包的本数和包数如下表。
每包的本数/本 10 20 40
包数/包 60 30 15
(1)判断每包的本数和包数是不是成反比例,并说明理由。
(2)如果打包成6包,那么每包多少本?
【答案】(1)10×60=20×30=40×15=600,每包的本数和包数的乘积一定,所以每包的本数和包数成反比例。
(2)100本。
【分析】(1)根据每包的本数和包数的乘积一定,确定每包的本数和包数成反比例。
(2)根据总本数÷包数=每包的本数列除法算式解答。
【解答】解:(1)10×60=20×30=40×15=600,每包的本数和包数的乘积一定,所以每包的本数和包数成反比例。
(2)10×60÷6=100(本)
答:每包100本。
【点评】两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例;若既不是比值一定也不是乘积一定,两种量不成比例。
51.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 4 9 16
所需小正方形的数量/个 216 96 54
(1)每个小正方形的面积与所需小正方形的数量成 反 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
【答案】见试题解答内容
【分析】(1)每个小正方形的面积×小正方形的数量=长方形彩纸的面积;长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)长方形彩纸的面积=36×需要小正方形个数,由此解答。
【解答】解:(1)长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)设需要多x个小正方形。
36x=216×4
36x÷36=216×4÷36
x=24
答:(1)每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)需要24个小正方形。
故答案为:反,24。
【点评】解决此题关键是根据比值一定或乘积一定,先列出比例,进而根据比例的性质先把比例式转化为乘积式来解比例得解;注意等号要对齐。
52.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出甲车行驶的路程与行驶时间同时扩大或缩小的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)由图象可知:行驶150千米的路程甲车用的时间少,所以速度较快;据此解答即可.
【解答】解:(1)两辆车子所行的路程和时间成比例,因为是一条直线,所以成正比例;
(2)由图象可知:甲行驶150km,用4.2小时,乙行驶150km,用4.4小时,
4.2<4.4,
路程相同,用的时间越少,速度较快,即甲汽车的行驶速度快些;
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的比值一定,这两种量成正比例.
53.每5m花布售价40元.
花布长度/m 1 2 3 4 5 6 7 8
总价/元 40
①把上表填完整.
②花布总价和长度是否成正比例?为什么?
【答案】见试题解答内容
【分析】①根据总价÷数量=单价,先求出每米布的售价,再根据总价=单价×数量,分别求出不同花布长度的价格即可.
②花布的长度与总价成正比例,因总价:数量=单价(一定),花布的长度与总价的比值一定,所以成正比例关系.
【解答】解:①40÷5=8(元)
1×8=8(元)
2×8=16(元)
3×8=24(元)
4×8=32(元)
6×8=48(元)
7×8=56(元)
8×8=64(元)
花布长度/m 1 2 3 4 5 6 7 8
总价/元 8 16 24 32 40 48 56 64
②花布总价和长度成正比例,因总价:数量=单价(一定),花布的长度与总价的比值一定,所以成正比例关系.
【点评】此题重点考查用正比例的意义来辨识成正比例的量.
54.王叔叔要把一张100元换成小面值的人民币.
面值/元 1 2 5 10 20 50
数量/张
(1)把表填写完整.
(2)人民币面值和张数成反比例吗?为什么?
【答案】见试题解答内容
【分析】(1)100×1=50×2=5×20=10×10=20×5=50×2=100元,据此即可解答;
(2)这个乘积表示面值与张数的积一定,即面值×张数=总值(一定);依据反比例的意义可得:面值与张数是一对相关联的量,且面值与张数的积一定,则面值与张数成反比例.
【解答】解:(1)填表如下:
面值/元 1 2 5 10 20 50
张数/张 100 50 20 10 5 2
(2)100×1=50×2=5×20=10×10=20×5=50×2=100元;这个乘积表示面值与张数的积一定,即面值×张数=总值(一定);因为面值与张数是一对相关联的量,且面值与张数的积一定,则面值与张数成反比例.
【点评】此题主要考查反比例的意义及其实际应用.
55.判断下面每题中的两种量是否成正比例关系,并说明理由.
(1)全班人数一定,出勤人数与缺勤人数;
(2)《光明日报》的单价一定,总价与数量.
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:(1)因为出勤人数+缺勤人数=全班的人数(一定)
所以全班人数一定,出勤人数与缺勤人数不成比例;
(2)因为:总量÷数量=单价(一定),
所以总价和数量成正比例.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
56.A、B两种商品的价格之比为7:2,如果它们的价格分别上涨60元后,价格之比为5:2,这两种商品原来的价格各是多少?
【答案】A原来的价格是315元,B原来的价格各是90元。
【分析】根据题意知道,A、B两种商品的价格差不会变化,由此根据“A、B两种商品的价格之比为7:2,”,知道原来A占价格差的,再根据“价格之比是5:2”知道后来A占价格差的,由此用60除以(),即可求出价格差,进而求出这两种商品原来的价格。
【解答】解:价格差是:
60÷()
=60
=225(元)
A原来的价格是:
225
=225
=315(元)
B原来的价格:315﹣225=90(元)
答:A原来的价格是315元,B原来的价格各是90元。
【点评】解答此题的关键是,根据价格差不变化,将比转化为分率,统一单位“1”,再根据基本的数量关系解决问题。
57.某物流公司将一批货物运往一家加工厂,且要一次性把所有货物全部运出,车辆的载质量与所需车辆的数量如表所示。
车辆的载质量/t 2.5 3 5 10
所需车辆的数量/辆 48 40 24 12
(1)车辆的载质量和所需车辆的数量成什么比例?如果用载质量为6t的车来运,那么一共需要多少辆?
(2)如果用15辆车来运,那么每辆车要运多少吨?
【答案】(1)反比例;20辆;(2)8吨。
【分析】(1)由统计表中的数量可以看出,车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例;运用总重量除以6就是运用卡车的辆数;
(2)运用总重量除以卡车的量数15就是每辆卡车运多少吨。
【解答】解:(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例。
120÷6=20(辆)
答:车辆的载质量和所需车辆的数量成反比例,一共需要20辆。
(2)120÷15=8(吨)
答:每辆卡车运8吨。
【点评】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题.同时考查了学生理解分析问题的能力。
58.下图表示一根水管不停地向水箱内注水时,水箱内水的体积的变化情况.
(1)水箱内水的体积与注水的时间成正比例吗?为什么?
(2)利用图象估一估,10分能注水多少升?注水45升需要多少分?再实际计算一下.
【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出水箱内水的体积与注水的时间(或缩小)的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)根据折线统计图可知,注水时间10分钟时,统计表中对应的水的体积为20升,即注水10分钟时水箱内的水的体积为20升,同理如果水要达到45升,需要注水22.5分钟.
【解答】解:(1)水箱内水的体积与注水的时间成正比例,因为水箱内水的体积与注水的时间的比值一定,且对应在一条直线上;
(2)45÷(10÷5)=22.5(分),
由图象可知10分能注水20升;注水45升需要22.5分.
【点评】此题考查借助直观的图象,辨识两种相关联的量成什么比例,只要图象是一条直线的,就成正比例;图象是一条曲线的,就成反比例;再根据成什么比例解决其它的问题.
59.一个平行四边形的面积是24m2,用x和y表示它的底和高.x与y成什么比例关系?如果把它们的关系用图象表示出来,那么它的图象是一条直线吗?
【答案】见试题解答内容
【分析】根据平行四边形的面积=底×高,即xy=24,可判断底和高的关系;再根据它们的关系判断出图象的形状.
【解答】解:因为xy=24,是乘积一定,所以y与x成反比例关系;
如果把它们的关系用图象表示出来,那么它的图象是一条曲线.
答:x与y成反比例关系,如果把它们的关系用图象表示出来,那么它的图象不是一条直线.
【点评】此题考查了两个量成何比例的方法,即如果两个量的比值一定,则这两个量成正比例,如果两个量的乘积一定,这两个量就成反比例.
60.“六一”那天,芳芳和小朋友们一起骑车去动物园玩.下面的图象表示的是她骑车的路程和时间的关系.
(1)芳芳骑车行驶的路程和时间成正比例吗?为什么?
(2)看图估计,行2.5千米大约用多少分钟?
【答案】见试题解答内容
【分析】(1)根据折线统计图可知,芳芳骑车行驶的路程和时间成正比例,因为速度一定,路程与时间成正比;
(2)芳芳行2.5千米时大约用了30÷2=15分钟.
【解答】解:(1)芳芳骑车行驶的路程和时间成正比例,因为速度一定,路程与时间成正比
1.一辆汽车两次行驶的路程与耗油量如下表:
行驶路程/km 24 96
耗油量/L 2 8
(1)分别写出每次行驶路程与耗油量的比值,判断这两个比能否组成比例.
(2)分别写出两次耗油量与对应行驶路程的比值,看看这两个比能否组成比例.
2.被除数一定,商和除数成 比例。
3.一种硬笔书法练习本,数量和总价的关系如表.
数量/本 1 2 3 4 5 6 …
总价/元 4 8 12 16 20 24 …
(1)在图中,描出总价与数量之间的对应点,并连接各点.
(2)总价与数量有什么关系?为什么?
4.如图的图象表示长颈鹿的奔跑情况.
(1)长颈鹿的奔跑路程与奔跑时间成 比例关系.
(2)请你计算一下,长颈鹿16分钟跑多少千米?
5.如图中线段AB表示一辆汽车行驶的路程与时间的关系.
①这辆汽车行驶了多长时间?行驶了多少千米?
②这辆汽车2.5小时行驶了多少千米?
③这辆汽车行驶900km要多长时间?
6.装配一批机器,每天装配的数量和需要的天数如下表。
每天装配的数量/台 40 80 100 160 200 400
需要的时间/天 40 20 16 10 8 4
(1)每天装配的数量和需要的时间成反比例关系吗?说明理由。
(2)如果每天装配64台,需要多少天装配完?
7.一辆变速自行车,前齿轮有2个,后齿轮有6个,前齿轮的齿数分别是40和36,后齿轮的齿数分别是32、30、28、26、24、20.
(1)这辆自行车能变化出多少种不同的速度?(先填表,再解答)
(2)蹬同样的圈数,要使自行车骑得最远,前、后齿轮的齿数比应是多少?
前齿轮齿数/前、后齿轮齿数比/后齿轮齿数 40 36
32
30
28
26
24
20
8.用24个边长1cm的小正方形,你能拼成几种不同的长方形?
(1)认真思考,完成表格。
长/cm
宽/cm
(2)从表中,你发现长和宽有怎样的比例关系?
9.四名同学都看了《少年学党史》这本书。请填写出每人看完这本书需要的天数。
郑小强 张小华 李小虹 王小新
每天看的页数 6 10 15 20
看的天数 30
照这样的速度看了3天,他们各看了多少页?还剩下多少页?
郑小强 张小华 李小虹 王小新
已看的页数
剩下的页数
题中,每天看的页数和看的天数 比例,已看的页数和剩下的页数 比例。
10.一列火车匀速行驶时,路程与时间的关系如表.
时间/小时 1 2 3 4 5 …
路程/千米 120 240 …
(1)完成上表.
(2)根据表格中的数据,这列火车行驶的路程与时间成什么比例?
(3)如果A、B两城相距420千米,需要多少小时可以从A城到达B城?
11.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量/辆 1 2 3 4 5 6 7
运货质量/吨 4 8 12 16 20 24 28
(1)表中 和 是两种相关联的量, 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
12.已知两个数M、N满足等式9N,数M与N成什么比例关系?请说明理由.
13.一辆汽车在高速公路上行驶的路程与耗油量的关系如下表:
行驶路程/km 50 100 150 200 250 …
耗油量/L 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来.
(2)这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350千米的耗油量.
(4)这辆汽车出发时油箱里有汽油40升,如果汽车要在高速公路上行驶460千米,你认为司机在途中需要加油吗?
14.如图的图象反映的是购买两种练习本的数量和总价的变化情况.
(1)购买甲种练习本的数量和总价是否成正比例?乙种呢?
(2)估计一下,买5本甲种练习本多少元?2.8元可以买几本甲种练习本?
(3)从图上看哪种练习本便宜些?2.4元可以买两种练习本各多少本?
15.兰兰坐爸爸开的车去看爷爷,她每过10分钟看一次里程表上的读数,结果如下:
时间 9:10 9:20 9:30 9:40 9:50 …
里程表读数/km| 31220 31235 31250 31265 31280 …
(1)这辆汽车行驶的路程和时间之间有什么关系?它们成正比例关系吗?为什么?
(2)如果9:50时离爷爷家还有45千米,照这样的速度,他们在什么时刻可以到达爷爷家?
16.认真观察图像,回答问题。
(1)图像中这两种量成正比例关系吗?为什么?
(2)根据所列出的两种量的关系。完成下表。
x 1 2.5 15
y 200
17.(1)分别写出图中两个长方形长与长的比和宽与宽的比,并求比值,然后判断这两个比能否组成比例,若能组成比例,请把这个比例写出来.
(2)分别写出图中每个长方形长与宽的比,并求比值,然后判断这两个比能否组成比例,若能组成比例,请把这个比例写出来.
18.一种花布的数量和总价如表.
数量/m 1 2 3 4 5 6 7 ……
总价/元 8 16 24 32 40 48 56 ……
(1)表中的总价和数量成正比例关系吗?为什么?
(2)在如图中描出表示数量和对应总价的点,然后把它们连起来,并说说图象的特点.
(3)利用图象回答,买2.5m花布需要多少元?68元能买多少米花布?
19.妈妈带的钱可以买单价为30元的猪肉6kg或单价为60元的牛肉3kg。
(1)妈妈一共带了多少钱?
(2)如果买单价为72元的羊肉,可以买多少千克?
(3)总价一定时,单价和数量成什么比例?用等式表示出它们的关系。
20.一艘轮船从甲港开到乙港,3时行驶了75km.从乙港开到丙港,5时行驶了125km.
(1)分别求轮船从甲港开到乙港,从乙港开到丙港的速度.
(2)轮船行驶的路程和所用时间成什么比例?
(3)用等式把题目里的数量关系表示出来.
21.明明家的鱼缸有A,B两根进水管,先打开A管,中途打开B管。如图表示从开始加水到蓄满水的进水时间和鱼缸中水的体积的关系。
(1)从0分到6分,鱼缸中水的体积和进水时间成比例吗?如果成,成什么比例?如果不成比例,理由是什么?
(2)A管每分进水多少升?B管呢?
22.如图的图象反映的是老虎和狮子的食肉情况.
(1)老虎的食肉量与时间成正比例吗?狮子呢?
(2)估计一下,老虎和狮子8天各食肉多少千克?
(3)哪种动物每天的食肉量较少?
23.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是 元.
②12瓶的总价是 元.
③ 瓶的总价是36元.
24.某物流公司要将一批货物运往加工厂,如果要一次把这些货物全部运走,货车的载质量与所需车辆的数量如下表。
载质量/吨 2.5 3 5
数量/辆 48 40 24
(1)货车的载质量与所需车辆的数量成反比例吗?为什么?
(2)如果用载质量为4.8吨的货车来运,一共需要多少辆?
25.如图表示某工厂中甲、乙两个车间加工的零件数与时间的关系.
(1)乙车间生产的零件数与时间成正比例吗?为什么?
(2)如果生产8万个零件,那么乙车间比甲车间少用几个月?
26.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/cm2 900 1800 3600
所需地砖的数量/块 600 300 150
(1)所需地砖数量与每块地砖的面积成 比例关系。
(2)如果采用边长为50cm的方砖铺这间教室,需要多少块方砖?(用比例的方法解答)
27.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t 2.5 3 5 10
数量/辆 48 40
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
28.下面是某学校一个漏水的水龙头的滴水情况统计表。
滴水量/mL 20 40 60 80 100 ……
时间/分 1 2 3 4 5 ……
(1)滴水量和时间成 比例。
(2)这个水龙头每时滴水多少升?
(3)如果用一个底面积是10dm2,高是3dm的圆柱形水桶接漏的水,那么多长时间能接满?(水桶的厚度忽略不计)
29.判断下列各题中的两个量是否成比例关系.若成,成什么比例关系?
(1)每小时加工零件数一定,加工时间和加工零件总数.
(2)从甲地去乙地,已行的路程和未行的路程.
(3)圆的直径和周长.
(4)已知x(y≠0),x和y.
30.下面的图象表示小强从甲地到乙地不同的速度和所对应的时间。
(1)在这个过程中,哪种量没有变?
(2)速度和所对应的时间成什么比例关系?
(3)不计算,观察图象,如果每小时行40km,那么从甲地到乙地大约需要多少小时?
31.如图,甲、乙两车运货的吨数与次数的关系如图.
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
32.判断下面各题中的两种量是否成比例?成什么比例?为什么?
(1)小麦的出粉率一定,小麦的总重量和出粉的重量。
(2)每箱木瓜的个数一定,运来木瓜的箱数和木瓜的总个数。
(3)房间的面积一定,铺地砖的块数与每块地砖的面积。
33.把相同体积的水倒入底面积不同的杯子.
水的高度/cm 30 20 15 10 5 …
杯子的底面积/cm2 10 15 20 30 60 …
水的高度和杯子的底面积成反比例吗?为什么?
34.配制一种盐水,水的质量总是比盐水的质量少15%,盐的质量与盐水的质量成正比例吗?
35.某厂要生产一批豆浆机,平均每天产量和所需时间如表。
平均每天产量/台 200 300 500
所需时间/天 75 50 30
(1)平均每天产量和所需时间成 比例。
(2)现要在20天内完成生产任务,平均每天产量至少要达到多少台?
36.妈妈买来一袋橡皮泥,平平全部用来捏大小相同的圆锥,正好没有剩余.圆锥的个数与每个圆锥所用橡皮泥的体积是否成反比例?为什么?
37.某童车厂装配一批童车,每天装配的数量和需要的时间如表。
每天装配的数量/辆 60 90 120 180 360 …
时间/天 60 40 30 20 10 …
(1)判断每天装配的数量和时间是否成反比例,并说明理由。
(2)如果每天装配200辆,多少天可以装配完这批童车?
38.科技小组制作了一个弹簧秤,弹簧的长度是8厘米。经验证,弹簧的长度与所挂钩码的质量存在如下关系:
弹簧长度/cm 8 9 10 11 ……
钩码质量/kg 0 2 4 6 ……
(1)钩码的质量和弹簧伸长的长度成什么比例关系?
(2)小亮用科技小组制作的这个弹簧秤称一个物体,弹簧的长度是14.8cm,这个物体的质量是多少千克?(用比例知识解答)
39.判断下面每题中的两种量是不是成正比例,并说明理由.
(1)小新跳高的高度和他的身高.
(2)长方形的宽一定,它的面积和长.
(3)小麦每公顷产量一定,小麦的公顷数和总产量.
40.小牛和大牛吃肥肉,原来小牛和大牛吃的肉块数之比为2:5,后来小牛又吃了5块,大牛也又吃了2块,此时小牛和大牛吃的肉块数之比为5:9,求原来两人各自吃了多少块肥肉?
41.新冠肺炎疫情期间,口罩需求量大幅上升。某工厂接到任务紧急生产一批口罩,下面是每时生产口罩的数量与完成任务总共需要的时间的关系。
每时生产口罩的数量/万只 2 3 4 6
时间/时 72 48 36 24
(1)每时生产口罩的数量与时间有什么关系?(1分)
(2)如果每时生产8万只口罩,那么完成这项任务一共需要多少时?(4分)
42.用一些纸装订同样的练习本,每本用纸的张数和装订的本数如表。
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40
(1)将如表补充完整。
(2)每本用纸张数和装订本数是否成反比例关系?为什么?
(3)如果用这些纸装订成50本练习本(每本用纸张数相同),每本用纸多少张?
43.如图图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)实验小学食堂用煤的天数和用煤量是否成正比例?
(2)根据图象判断,食堂5天要用煤多少吨?2.4吨煤可以用多少天?
44.某工厂有一批煤,每天烧煤的质量和可烧的时间关系如下表。
每天烧煤的质量/吨 0 3 6 9 15 20 …
可烧的时间/天 0 30 15 10 6 4.5 …
(1)判断每天烧煤的质量和可烧的时间是不是成反比例,并说明理由。
(2)如果该工厂平均每天烧煤的质量是5吨,那么这批煤可烧多少天?
45.
时间/时 1 2 3 4 5 6 …
路程/千米 90 …
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
46.王老师准备用72元钱去买笔记本.如果每本价格是2元,能买多少本?如果每本价格是3元、4元或6元呢?
每本价格/元 2 3 4 6
数量/本
观察上表,你有什么发现?
47.书房的面积是16m2,刚好用了32块地砖,卧室的面积是20m2,用同样的地砖,需要多少块?
48.四名同学到超市购买练习本,先填表,再回答问题.
(1)他们都带了6元,购买了不同品种的练习本.
张华 李浩 王佟 陈刚
单价/(元/本) 0.60 1.20 1.50 2.00
购买的数量/本
他们带的钱数相同,练习本的单价和购买的数量成什么比例?为什么?
(2)他们都买单价是0.60元/本的练习本.
张华 李浩 王佟 陈刚
购买的数量/本 2 5 8 9
用去的金额/元
购买的练习本单价相同,购买的数量和用去的金额成什么比例?为什么?
(3)已知他们买练习本用去的金额,且每人都带了6元.
张华 李浩 王佟 陈刚
用去的金额/元 0.6 1.2 1.5 2
剩下的金额/元
带的金额相同,用去的金额和剩下的金额成比例吗?为什么?
49.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数 20 15
10
需要的天数
12 15
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
50.邮局准备把一批《百科全书》打包寄给山区的小朋友。每包的本数和包数如下表。
每包的本数/本 10 20 40
包数/包 60 30 15
(1)判断每包的本数和包数是不是成反比例,并说明理由。
(2)如果打包成6包,那么每包多少本?
51.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 4 9 16
所需小正方形的数量/个 216 96 54
(1)每个小正方形的面积与所需小正方形的数量成 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
52.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
53.每5m花布售价40元.
花布长度/m 1 2 3 4 5 6 7 8
总价/元 40
①把上表填完整.
②花布总价和长度是否成正比例?为什么?
54.王叔叔要把一张100元换成小面值的人民币.
面值/元 1 2 5 10 20 50
数量/张
(1)把表填写完整.
(2)人民币面值和张数成反比例吗?为什么?
55.判断下面每题中的两种量是否成正比例关系,并说明理由.
(1)全班人数一定,出勤人数与缺勤人数;
(2)《光明日报》的单价一定,总价与数量.
56.A、B两种商品的价格之比为7:2,如果它们的价格分别上涨60元后,价格之比为5:2,这两种商品原来的价格各是多少?
57.某物流公司将一批货物运往一家加工厂,且要一次性把所有货物全部运出,车辆的载质量与所需车辆的数量如表所示。
车辆的载质量/t 2.5 3 5 10
所需车辆的数量/辆 48 40 24 12
(1)车辆的载质量和所需车辆的数量成什么比例?如果用载质量为6t的车来运,那么一共需要多少辆?
(2)如果用15辆车来运,那么每辆车要运多少吨?
58.下图表示一根水管不停地向水箱内注水时,水箱内水的体积的变化情况.
(1)水箱内水的体积与注水的时间成正比例吗?为什么?
(2)利用图象估一估,10分能注水多少升?注水45升需要多少分?再实际计算一下.
59.一个平行四边形的面积是24m2,用x和y表示它的底和高.x与y成什么比例关系?如果把它们的关系用图象表示出来,那么它的图象是一条直线吗?
60.“六一”那天,芳芳和小朋友们一起骑车去动物园玩.下面的图象表示的是她骑车的路程和时间的关系.
(1)芳芳骑车行驶的路程和时间成正比例吗?为什么?
(2)看图估计,行2.5千米大约用多少分钟?
期末专项培优 正比例和反比例
参考答案与试题解析
1.一辆汽车两次行驶的路程与耗油量如下表:
行驶路程/km 24 96
耗油量/L 2 8
(1)分别写出每次行驶路程与耗油量的比值,判断这两个比能否组成比例.
(2)分别写出两次耗油量与对应行驶路程的比值,看看这两个比能否组成比例.
【答案】见试题解答内容
【分析】(1)根据题意,先写出两次行驶路程与耗油数量的比,然后分别求出比值,通过比较比值判断出两次行驶路程与耗油数量的比能否组成比例.如果比值相等,能组成比例,反之则不能.
(2)先写出两次行驶的路程的比,与两次耗油量的比,然后分别求出比值,通过比较比值判断出两次行驶路程与耗油数量的比能否组成比例.如果比值相等,能组成比例,反之则不能.
【解答】解:(1)行驶路程与耗油数量的比分别是:
24:2
96:8
24:2=12
96:8=12
12=12
所以这两个比能组成比例.
(2)两次耗油量与对应行驶路程的比分别是:
2:24
8:96
2:24
8:96
所以这两个比能组成比例.
【点评】解答此题的关键是明确比例的判定方法,即两个比的比值相同就能组成比例,然后再进一步解答.
2.被除数一定,商和除数成 反 比例。
【答案】反比例。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:因为每班人数×班数=总人数(一定),是对应的乘积一定,所以每行人数与行数成反比例;
故答案为:反。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
3.一种硬笔书法练习本,数量和总价的关系如表.
数量/本 1 2 3 4 5 6 …
总价/元 4 8 12 16 20 24 …
(1)在图中,描出总价与数量之间的对应点,并连接各点.
(2)总价与数量有什么关系?为什么?
【答案】见试题解答内容
【分析】(1)首先根据表中的数据描出各点,然后顺次连接个点即可.
(2)因为单价(一定),所以总价和数量成正比例.
【解答】解:(1)作图如下:
(2)4
因为单价(一定),所以总价和数量成正比例.
【点评】此题考查的目的是理解掌握正比例的意义及应用,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(即两个数的商)一定,这两种就叫做成正比例的量,它们的关系就是正比例关系.
4.如图的图象表示长颈鹿的奔跑情况.
(1)长颈鹿的奔跑路程与奔跑时间成 正 比例关系.
(2)请你计算一下,长颈鹿16分钟跑多少千米?
【答案】见试题解答内容
【分析】(1)通过观察图可知,速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,据此列比例解答.
【解答】解:(1)因为速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,
5x=4×16
x
x=12.8
答:长颈鹿16分钟跑12.8千米.
故答案为:正.
【点评】此题考查的目的是理解掌握正比例的意义及应用,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(即两个数的商)一定,这两种就叫做成正比例的量,它们的关系就是正比例关系.
5.如图中线段AB表示一辆汽车行驶的路程与时间的关系.
①这辆汽车行驶了多长时间?行驶了多少千米?
②这辆汽车2.5小时行驶了多少千米?
③这辆汽车行驶900km要多长时间?
【答案】见试题解答内容
【分析】①找出这辆汽车的终点,根据图表找出对应的时间和路程.
②先根据“路程÷时间=速度”求出汽车的速度,进而根据“速度×时间=路程”进行解答即可.
③先根据“路程÷速度=时间”求出汽车行驶900km所需时间.
【解答】解:①这辆汽车的终点,根据图表找出对应的时间是3小时,路程是180千米.
答:这辆汽车行驶了3小时,行驶了180千米.
②180÷3=60(km/h),60×2.5=150(km).
答:这辆汽车2.5小时行驶了150千米.
③900÷60=15(h).
答:这辆汽车行驶900km要15小时
【点评】此题考查了学生从统计图中挖掘信息以及处理数据的能力,同时考查了正反比例的知识和对行程问题的掌握.
6.装配一批机器,每天装配的数量和需要的天数如下表。
每天装配的数量/台 40 80 100 160 200 400
需要的时间/天 40 20 16 10 8 4
(1)每天装配的数量和需要的时间成反比例关系吗?说明理由。
(2)如果每天装配64台,需要多少天装配完?
【答案】(1)每天装配的数×需的时间=总工作量(一定),所以每天装配的数量和需要的时间成反比例;(2)25天。
【分析】(1)根据表可知每天装配的数与需的时间的乘积一定,据此可的每天装配的数量和需要的时间成反比例;
(2)由(1)可知,每天装配的数量和需要的时间成反比例,用它们的乘积除以每天装配的台数即可解答。
【解答】解:(1)40×40=1600(台)
80×20=1600(台)
100×16=1600(台)……
即:每天装配的数×需的时间=总工作量(一定),所以每天装配的数量和需要的时间成反比例。
(2)40×40÷64
=1600÷64
=25(天)
答:需要25天装配完。
【点评】掌握反比例的意义是解决此题的关键。
7.一辆变速自行车,前齿轮有2个,后齿轮有6个,前齿轮的齿数分别是40和36,后齿轮的齿数分别是32、30、28、26、24、20.
(1)这辆自行车能变化出多少种不同的速度?(先填表,再解答)
(2)蹬同样的圈数,要使自行车骑得最远,前、后齿轮的齿数比应是多少?
前齿轮齿数/前、后齿轮齿数比/后齿轮齿数 40 36
32
30
28
26
24
20
【答案】见试题解答内容
【分析】(1)根据比的定义计算即可求解;
(2)根据变速自行车原理,前后齿轮数的比值越大,前齿轮转一圈,后齿轮所转的圈数就越多,所以得出前齿轮齿数最多,后齿轮齿数最少时自行车跑得最远.
【解答】解:(1)填表如下:
前齿轮齿数/前、后齿轮齿数比/后齿轮齿数 40 36
32 5:4 9:8
30 4:3 6:5
28 10:7 9:7
26 20:13 18:13
24 5:3 3:2
20 2:1 9:5
故这辆自行车能变化出12种不同的速度;
(2)蹬同样的圈数,要使自行车骑得最远,前、后齿轮的齿数比应是2:1.
【点评】主要依据变速自行车原理来组合,即前后齿轮数的比值越大,前齿轮转一圈,后齿轮所转的圈数就越多.
8.用24个边长1cm的小正方形,你能拼成几种不同的长方形?
(1)认真思考,完成表格。
长/cm
宽/cm
(2)从表中,你发现长和宽有怎样的比例关系?
【答案】
长/cm 24 12 8 6
宽/cm 1 2 3 4
反。
【分析】(1)24的因数有1,2,3,4,6,8,12,24,用24个小正方形拼成的长方形,由此进行解答;
(2)判断两个相关的量之间成什么关系,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,就成反比例,即可解答。
【解答】解:(1)根据分析知拼成后图形的面积不变,拼成后长方形的长和宽可分下列情况:
长/cm 24 12 8 6
宽/cm 1 2 3 4
所以能拼成4种不同的长方形;
(2)长方形的面积=长×宽
24×1=24(平方厘米)
12×2=24(平方厘米)
8×3=24(平方厘米)
6×4=24(平方厘米)
面积一定,就是乘积一定,长和宽成反比例关系。
【点评】本题的关键是根据拼成后面积不变,分情况讨论组成长方形的长和宽
9.四名同学都看了《少年学党史》这本书。请填写出每人看完这本书需要的天数。
郑小强 张小华 李小虹 王小新
每天看的页数 6 10 15 20
看的天数 30
18
12
9
照这样的速度看了3天,他们各看了多少页?还剩下多少页?
郑小强 张小华 李小虹 王小新
已看的页数
18
30
45
60
剩下的页数
162
150
135
120
题中,每天看的页数和看的天数 成反 比例,已看的页数和剩下的页数 不成 比例。
【答案】18,12,9;18,30,45,60;162,150,135,120;成反,不成。
【分析】(1)用郑小强每天看的页数6×看的总天数30=这本书的总页数,用总页数分别除以张小华、李小虹、王小新每天看的页数,就是他们分别看的天数;
(2)分别用郑小强、张小华、李小虹、王小新每天看的页数乘3天,就是他们3天各自看的页数,再用郑小强每天看的页数6×看的总天数30=这本书的总页数,用总页数减去他们3天各自看的页数,就是他们各自剩下的页数;判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:(1)30×6=180(页)
180÷10=18(天)
180÷15=12(天)
180÷20=9(天)
答:张小华需要看18天,李小虹需要看12天,王小新需要9天。
(2)6×3=18(页)
10×3=30(页)
15×3=45(页)
20×3=60(页)
6×30=180(页)
180﹣18=162(页)
180﹣30=150(页)
180﹣45=135(页)
180﹣60=120(页)
答:他们分别看了18页、30页、45页、60页,分别剩下162页、150页、135页、120页。
因为每天看的页数×看的天数=180(页)(一定),乘积一定,所以每天看的页数和看的天数成反比例;
已看的页数+剩下的页数=180(页)(一定),和一定,所以已看的页数和剩下的页数不成比例。
故答案为:18,12,9;18,30,45,60;162,150,135,120;成反,不成。
【点评】明确每天看的页数×看的天数=看的页数以及辨识成正、反比例的量的方法是解题的关键。
10.一列火车匀速行驶时,路程与时间的关系如表.
时间/小时 1 2 3 4 5 …
路程/千米 120 240 …
(1)完成上表.
(2)根据表格中的数据,这列火车行驶的路程与时间成什么比例?
(3)如果A、B两城相距420千米,需要多少小时可以从A城到达B城?
【答案】见试题解答内容
【分析】(1)根据路程、速度、时间三者之间的关系即可分别求出火车的路程,然后填表.
(2)根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就是成反比例的量,它们的关系是反比例关系.即形如xy=k(一定),x、y是成反比例的量,x与y成反比例关系.依此即可求解.
(3)根据时间=路程÷速度即可解答.
【解答】解:(1)120×3=360(千米)
120×4=480(千米)
120×5=600(千米)
填表如下:
时间/小时 1 2 3 4 5 …
路程/千米 120 240 360 480 600 …
(2)因为路程÷时间=速度(一定),所以这列火车行驶的路程与时间成正比例;
(3)420÷120=3.5(小时)
答:需要3.5小时可以从A城到达B城.
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
11.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量/辆 1 2 3 4 5 6 7
运货质量/吨 4 8 12 16 20 24 28
(1)表中 汽车数量 和 运货质量 是两种相关联的量, 运货质量 随着 汽车数量 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
【答案】见试题解答内容
【分析】(1)根据题意知:表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
【解答】解:(1)表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
故答案为:汽车数量;运货质量;运货质量;汽车数量.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
12.已知两个数M、N满足等式9N,数M与N成什么比例关系?请说明理由.
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为9N,
9×9×MN×9×M
所以MN=81(一定),
即对应的乘积一定;
所以数M与N成反比例关系.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
13.一辆汽车在高速公路上行驶的路程与耗油量的关系如下表:
行驶路程/km 50 100 150 200 250 …
耗油量/L 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来.
(2)这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350千米的耗油量.
(4)这辆汽车出发时油箱里有汽油40升,如果汽车要在高速公路上行驶460千米,你认为司机在途中需要加油吗?
【答案】见试题解答内容
【分析】(1)根据统计表中的数据完成统计图.
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;由此解答即可.
(3)根据耗油量=汽车行驶的路程除以每升油行驶的路程,计算即可.
(4)计算460千米需要多少升汽油,与40升进行比较,即可得出结论.
【解答】解:(1)统计图如下:
(2)50÷5=100÷10=150÷15=10(一定),即:汽车行驶的路程÷耗油量=每升油行驶的路程(一定),
所以这辆汽车行驶的路程和耗油量成正比例.
(3)350÷10=35(升)
答:这辆汽车行驶350千米的耗油量为35升.
(4)460÷10=46(升)
46>40
答:司机在途中需要加油.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
14.如图的图象反映的是购买两种练习本的数量和总价的变化情况.
(1)购买甲种练习本的数量和总价是否成正比例?乙种呢?
(2)估计一下,买5本甲种练习本多少元?2.8元可以买几本甲种练习本?
(3)从图上看哪种练习本便宜些?2.4元可以买两种练习本各多少本?
【答案】见试题解答内容
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
(2)估计买5本甲种练习本的价钱,先找到甲图象与数量5的交点,看看这个交点对应的数轴的数值即可解答,估计2.8元可以买几本甲种练习本,看2.8元与甲图象的交点所对应的数值.
(3)看1本对应的单价即可解答.先根据图象求两种练习本的单价,根据单价求2.4元买两种练习本的本数.
【解答】解:(1)甲:0.4÷1=0.8÷2=1.2÷3=0.4,即总价÷数量=单价(一定),所以甲种练习本的数量和总价成正比例;
乙:0.4÷2=0.8÷4=1.2÷6=0.2,即总价÷数量=单价(一定),所以乙种练习本的数量和总价成正比例.
(2)5本甲种练习本对应的价钱大约是2元
2.8元与甲种练习本对应的数量是7
答:5本乙种练习本的价钱是1元,2.8元可以买,7本甲种练习本.
(3)从图上看,1本书对应的本数的乙的单价低,所以乙种练习本便宜些.
3.2÷8=0.4(元/本)
2.4÷12=0.2(元/本)
2.4÷0.4=6(本)
2.4÷0.2=12(本)
答:乙种练习本便宜.2.4元可以买6本甲或12本乙练习本.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
15.兰兰坐爸爸开的车去看爷爷,她每过10分钟看一次里程表上的读数,结果如下:
时间 9:10 9:20 9:30 9:40 9:50 …
里程表读数/km| 31220 31235 31250 31265 31280 …
(1)这辆汽车行驶的路程和时间之间有什么关系?它们成正比例关系吗?为什么?
(2)如果9:50时离爷爷家还有45千米,照这样的速度,他们在什么时刻可以到达爷爷家?
【答案】见试题解答内容
【分析】(1)后面一个里程表读数减相邻的前一个里程表读数就是此时间段所行驶的路程.据此即可分别求出各时间段所行驶的路程.根据时间的推算,用后一个时刻减前一个相邻时刻就是此时间段的时间.通过计算可以发现时间段相同,所行驶的路程也相同.根据“速度=路程÷时间”,计算出这辆汽车的速度,如果速度相等,即一定,即路程÷时间=速度(一定),则路程与时间成正比例关系.
(2)根据“时间=路程÷速度”求出45千克路程所需要的时间,用9时50分加所用的时间就是到家的时刻.
【解答】解:(1)9时20分﹣9时10分=10分
31235﹣31220=15(km)
15÷10=1.5(km/分);
9时30分﹣9时20分=10分
31250﹣31235=15(km)
15÷10=1.5(km/分);
9时40分﹣9时30分=10分
31265﹣31250=15(km)
15÷10=1.5(km/分);
9时50分﹣9时40分=10分
31280﹣31265=15(km)
15÷10=1.5(km/分);
……
这辆汽车行驶的路程和所用时间的比值(商)一定,它们成正比例关系.
理由:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量,它们的关系是正比例关系.
(2)45÷1.5=30(分)
9时50分+30分=10时20分
10时20分即10:20
答:他们在10:20可以到达爷爷家.
【点评】此题主要是考查了两个方面的内容:正、反比例的辨析;时间的推算.
16.认真观察图像,回答问题。
(1)图像中这两种量成正比例关系吗?为什么?
(2)根据所列出的两种量的关系。完成下表。
x 1 2.5 15
y 200
【答案】(1)成正比例关系。
(2)20,50,10,300。
【分析】(1)正比例图像是一条直线,反比例图像是一条平滑的曲线。
(2)根据比值一定,求出对应的值,填入表中。
【解答】解:(1)图像是一条直线,所以两种量成正比例关系。
(2)
x 1 2.5 10 15
y 20 50 200 300
【点评】本题考查正比例图像的判断及根据图像解决问题,根据是根据图像分析数量关系。
17.(1)分别写出图中两个长方形长与长的比和宽与宽的比,并求比值,然后判断这两个比能否组成比例,若能组成比例,请把这个比例写出来.
(2)分别写出图中每个长方形长与宽的比,并求比值,然后判断这两个比能否组成比例,若能组成比例,请把这个比例写出来.
【答案】见试题解答内容
【分析】(1)先求得两个长方形长与长的比和宽与宽的比,进而化简比,并求比值,根据比例的意义判断能否组成比例,再把这个比例写出来即可.
(2)先求得每个长方形长与宽的比,进而化简比,并求比值,根据比例的意义判断能否组成比例,再把这个比例写出来即可.
【解答】解:(1)两个长方形长与长的比是2.5:1.5=5:3
两个长方形宽与宽的比是2:1.2=5:3
,
所以这两个长方形长与长的比和宽与宽的比能组成比例,为2.5:1.5=2:1.2.
(2)大长方形的长与宽之比是2.5:2=5:4
小长方形的长与宽之比是1.5:1.2=5:4
,
所以这两个长方形的长与宽之比能组成比例,为2.5:2=1.5:1.2.
【点评】此题考查用比例的性质辨识两个比能否组成比例,关键是看这两个比的比值是否相等,比值相等,就能组成比例,比值不相等,就不能组成比例.
18.一种花布的数量和总价如表.
数量/m 1 2 3 4 5 6 7 ……
总价/元 8 16 24 32 40 48 56 ……
(1)表中的总价和数量成正比例关系吗?为什么?
(2)在如图中描出表示数量和对应总价的点,然后把它们连起来,并说说图象的特点.
(3)利用图象回答,买2.5m花布需要多少元?68元能买多少米花布?
【答案】见试题解答内容
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示k(一定).
(1)通过计算总价与数量的比值是否一定,来判定总价与数量是否成正比例关系即可.
(2)描点,连线即可.
(3)利用图象看2.5m所对应的图象上的点所对应的总价是多少元即可,然后再看68元所对应的图象上的点所对应的数量是多少米即可.
【解答】解:(1)总价和数量成正比例关系.
因为8(一定),是比值一定,
所以总价和数量成正比例关系.
(2)
由图可知正比例关系的图象是一条射线.
(3)根据图象可知:买2.5m花布需要20元,68元能买米8.5米花布.
【点评】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值.还要学会利用数形结合的思想解决数学问题.
19.妈妈带的钱可以买单价为30元的猪肉6kg或单价为60元的牛肉3kg。
(1)妈妈一共带了多少钱?
(2)如果买单价为72元的羊肉,可以买多少千克?
(3)总价一定时,单价和数量成什么比例?用等式表示出它们的关系。
【答案】(1)180,(2)2.5,(3)反比例,单价×数量=总价(一定)。
【分析】(1)根据单价×数量=总价,列式解答即可;
(2)根据总价÷单价=数量,列式解答即可;
(3)总价一定时,看单价和数量是商一定还是积一定,如果是商一定就成正比例,如果是积一定则成反比例。
【解答】解:(1)30×6=180(元)
答:妈妈一共带了180元钱。
(2)180÷72=2.5(千克)
答:可以买2.5千克。
(3)单价×数量=总价(一定),所以总价一定时,单价和数量成反比例。
【点评】熟练掌握单价、数量、总价之间的关系以及辨识成正比例和反比例的量是解决此题的关键。
20.一艘轮船从甲港开到乙港,3时行驶了75km.从乙港开到丙港,5时行驶了125km.
(1)分别求轮船从甲港开到乙港,从乙港开到丙港的速度.
(2)轮船行驶的路程和所用时间成什么比例?
(3)用等式把题目里的数量关系表示出来.
【答案】见试题解答内容
【分析】(1)知道从甲港开到乙港的路程是75km,时间是3小时,利用“速度=路程÷时间”可求得从甲港开到乙港的速度; 同理可求得从乙港开到丙港的速度.
(2)由(1)可知速度(一定),可知行驶的路程和所用时间之间的关系.
(3)根据(2)中所成的比例关系表示出来即可.
【解答】解:从甲港开到乙港的速度:75÷3=25(千米/时).
从乙港开到丙港的速度:125÷5=25(千米/时).
答:轮船从甲港开到乙港,从乙港开到丙港的速度都是25千米/时.
(2)由(1)可知25(一定),是比值一定,所以轮船行驶的路程和所用时间成正比例.
(3)设s表示路程,t表示时间,v表示速度,则等量关系为:v.
【点评】此题考查成正比例的量的应用,理解速度,时间,路程之间的关系和正比例关系的意义是解题的关键.
21.明明家的鱼缸有A,B两根进水管,先打开A管,中途打开B管。如图表示从开始加水到蓄满水的进水时间和鱼缸中水的体积的关系。
(1)从0分到6分,鱼缸中水的体积和进水时间成比例吗?如果成,成什么比例?如果不成比例,理由是什么?
(2)A管每分进水多少升?B管呢?
【答案】(1)成比例,成正比例;
(2)A管每分进水1.2升,B管每分进水1.6升。
【分析】(1)从0分到6分,鱼缸中水的体积和进水时间的比值不变,所以鱼缸中水的体积和进水时间成比例,据此解答即可;
(2)从0分到6分只有A管进水,可求出A管每分进水多少升,从6分到12分A、B管同时进水,后6分钟的用进水量减去这段时间A管的进水量,就是这段时间B管的进水量,由此即可求出B管每分进水多少升。
【解答】解:(1)从0分到6分,鱼缸中水的体积和进水时间的比值不变,鱼缸中水的体积和进水时间成比例,成正比例。
(2)A管:7.2÷6=1.2(升)
B管:(24﹣7.2)÷(12﹣6)﹣1.2
=16.8÷6﹣1.2
=2.8﹣1.2
=1.6(升)
答:A管每分进水1.2升,B管每分进水1.6升。
【点评】熟练掌握正比例和反比例的判定方法,是解答此题的关键。
22.如图的图象反映的是老虎和狮子的食肉情况.
(1)老虎的食肉量与时间成正比例吗?狮子呢?
(2)估计一下,老虎和狮子8天各食肉多少千克?
(3)哪种动物每天的食肉量较少?
【答案】见试题解答内容
【分析】(1)老虎的食肉量与所用时间的比是:10:2.4=50:12=25:6(一定);所以老虎的食肉量与所用时间成正比例.狮子的食肉量与所用时间的比是:80:12=40:6=20:3(一定);所以狮子的食肉量与所用时间成正比例.
(2)过横轴上表示8天的点作纵轴的平行线与表示老虎食肉量与天数的直线相交,过交点作横轴的平行线,与纵轴的交点处的食肉量即表示老虎8天吃肉的千克数;同理,过横轴上表示8天的点作纵轴的平行线与表示狮子食肉量与天数的直线相交,过交点作横轴的平行线,与纵轴的交点处的食肉量即表示狮子8天吃肉的千克数.
(3)根据(2)计算出老虎、狮子每天的食肉量,通过比较即可得知.
【解答】解:(1)答:老虎的食肉量与所用时间是成正比例;狮子的食肉量与所用时间是成正比例.
(2)如图
答:老虎9天可以吃约36千克肉,狮子9天吃约60千克肉.
(3)33÷8≈4(千克)
53÷8≈6(千克)
6>4
答:狮子每天的食肉量多.
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.从图象也可以判断:表示正比例关系的图形是一直线,表示反比例关系的图象是曲线
23.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是 10 元.
②12瓶的总价是 24 元.
③ 18 瓶的总价是36元.
【答案】见试题解答内容
【分析】①仔细观察图表,5瓶的售价是10元;
②先利用所给的数据求出一瓶矿泉水的价格,再根据总价=单价×数量解答即可;
③先利用所给的数据求出一瓶矿泉水的价格,用数量=总价÷单价解答即可.
【解答】解:(1)5瓶的售价是10元.
(2)10÷5×12
=2×12
=24(元);
答:12瓶的售价是 24元.
(3)36÷(10÷5)
=36÷2
=18(瓶);
答:18瓶的售价是36元.
故答案为:10,24,18.
【点评】此题主要考查正比例的意义在生活实际中的灵活应用.
24.某物流公司要将一批货物运往加工厂,如果要一次把这些货物全部运走,货车的载质量与所需车辆的数量如下表。
载质量/吨 2.5 3 5
数量/辆 48 40 24
(1)货车的载质量与所需车辆的数量成反比例吗?为什么?
(2)如果用载质量为4.8吨的货车来运,一共需要多少辆?
【答案】(1)成反比例。理由是货车的载质量与所需车辆的数量的乘积一定。
(2)25辆。
【分析】(1)2.5×48=4×30=5×24=120,得出:车辆的载重量×所需车辆的数量=总重量,则车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例。
(2)设一共需要x辆卡车。因为车辆的载重量×所需车辆的数量=总重量(一定),所以4.8乘x的积等于2.5×48的积,据此即可解答。
【解答】解:(1)2.5×48=120(吨)
3×40=120(吨)
5×24=120(吨)
因为2.5×48=3×40=5×24=120(一定),也就是货车的载质量与所需车辆的数量的乘积一定,因此货车的载质量与所需车辆的数量成反比例。
答:成反比例。理由是货车的载质量与所需车辆的数量的乘积一定。
(2)3×40÷4.8
=120÷4.8
=25(辆)
答:一共需要25辆。
【点评】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题.同时考查了学生理解分析问题的能力。
25.如图表示某工厂中甲、乙两个车间加工的零件数与时间的关系.
(1)乙车间生产的零件数与时间成正比例吗?为什么?
(2)如果生产8万个零件,那么乙车间比甲车间少用几个月?
【答案】见试题解答内容
【分析】(1)判断生产的零件数与时间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;
(2)根据工作总量÷工效=工作时间,先分别求出甲、乙车间用的时间,再相减即可.
【解答】解:(1)由图意可知,2:1=2,4:2=2,6:3=2,8:4=2…,16:8=2,
工效是一定的,工作总量和工作时间的比值一定,所以乙车间生产的零件数与时间成正比例.
(2)乙生产8万个零件需要:8÷2=4(个月)
甲生产8万个零件需要:8÷(2÷2)=8(个月)
8﹣4=4(个月)
答:如果生产8万个零件,那么乙车间比甲车间少用4个月.
【点评】本题考查了比例的有关知识,解题的关键是从折线统计图中得到进一步解题的相关信息.
26.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖的数量如表。
每块地砖的面积/cm2 900 1800 3600
所需地砖的数量/块 600 300 150
(1)所需地砖数量与每块地砖的面积成 反 比例关系。
(2)如果采用边长为50cm的方砖铺这间教室,需要多少块方砖?(用比例的方法解答)
【答案】(1)反;(2)216。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)先求出边长为50cm的方砖的面积,根据所需地砖数量与每块地砖的面积成反比例关系,设需要x块方砖,根据题意列出比例式,解答即可。
【解答】解:(1)900×600=540000(cm )
1800×300=540000(cm )
3600×150=540000(cm )
即所需地砖数量×每块地砖的面积=教室的面积(一定),乘积一定,所以所需地砖数量与每块地砖的面积成反比例。
(2)设需要x块方砖。
50×50x=540000
2500x=540000
x=216
答:需要216块这样的方砖。
故答案为:反。
【点评】熟练掌握判断两个相关联的量之间成什么比例的方法以及应用反比例关系解决实际问题的方法是解题的关键。
27.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t 2.5 3 5 10
数量/辆 48 40
24
12
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
【答案】见试题解答内容
【分析】2.5×48=3×40=120,得出:运用车辆的载重量×所需车辆的数量=总重量,则用总重量分别除以5,10求出各用的辆数.填写统计表.
(1)由统计表中的数量可以看出,车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例.
(2)运用总重量除以6就是运用卡车的辆数.
(3)运用总重量除以卡车的量数15就是每辆卡车运多少吨.
【解答】解:3×40÷5
=120÷5
=24(辆)
3×40÷10
=120÷10
=12(辆)
载质量/t 2.5 3 5 10
数量/辆 48 40 24 12
(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,
所以车辆的载重量与所需车辆的数量成反比例.
(2)120÷6=20(辆)
答:用载重量6吨的卡车来运,一共需要20辆.
(3)120÷15=8(吨)
答:每辆卡车运8吨.
故答案为:24;12.
【点评】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题.同时考查了学生理解分析问题的能力.
28.下面是某学校一个漏水的水龙头的滴水情况统计表。
滴水量/mL 20 40 60 80 100 ……
时间/分 1 2 3 4 5 ……
(1)滴水量和时间成 正 比例。
(2)这个水龙头每时滴水多少升?
(3)如果用一个底面积是10dm2,高是3dm的圆柱形水桶接漏的水,那么多长时间能接满?(水桶的厚度忽略不计)
【答案】(1)正;(2)1.2升;(3)1500分钟。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)用每分钟的滴水量乘1小时,就是这个水龙头每时的滴水量;
(3)根据圆柱的体积=底面积×高,代入数据求出圆柱形水桶的体积,再除以每分钟的滴水量即可解答。
【解答】解:(1)因为20÷1=20(mL)
40÷2=20(mL)
60÷3=20(mL)
……
滴水量÷时间=20(mL)(一定),商一定,所以滴水量和时间成正比例。
(2)1小时=60分钟
20×60=1200(mL)
1200mL=1.2L
答:这个水龙头每时滴水1.2升。
(3)20毫升=0.02升=0.02立方分米
10×3÷0.02
=30÷0.02
=1500(分钟)
答:1500分钟能接满。
故答案为:正。
【点评】本题考查了判断两个相关联的量之间成什么比例的方法、工作量、工作效率、工作时间的关系以及圆柱体积的计算方法。
29.判断下列各题中的两个量是否成比例关系.若成,成什么比例关系?
(1)每小时加工零件数一定,加工时间和加工零件总数. 成正比例
(2)从甲地去乙地,已行的路程和未行的路程. 不成比例
(3)圆的直径和周长. 成正比例
(4)已知x(y≠0),x和y. 成反比例
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:(1)加工零件总数÷加工时间=每小时加工零件数(一定),是比值一定,所以加工的时间和加工零件总数成正比例;
(2)已行的路程+未行的路程=总路程(一定),是和一定,所以已行的路程和未行的路程不成比例;
(3)圆的周长÷直径=圆周率(一定),是比值一定,所以圆的直径和周长成正比例.
(4)因为x(y≠0),所以xy=3(一定)是乘积一定,符合反比例的意义,所以x与y成反比例.
故答案为:成正比例,不成比例,成正比例,成反比例.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
30.下面的图象表示小强从甲地到乙地不同的速度和所对应的时间。
(1)在这个过程中,哪种量没有变?
(2)速度和所对应的时间成什么比例关系?
(3)不计算,观察图象,如果每小时行40km,那么从甲地到乙地大约需要多少小时?
【答案】见试题解答内容
【分析】(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化。
(2)观察图象发现速度和时间的关系是反比例关系。
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时。
【解答】解:(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化。
(2)观察图象发现速度和时间的关系是反比例关系。
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时。
【点评】此题主要考查反比例的意义。解题的关键是掌握反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
31.如图,甲、乙两车运货的吨数与次数的关系如图.
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
【答案】见试题解答内容
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示k(一定).成正比例关系的图象是经过原点的一条直线.
(1)根据图中数据,算一算甲、乙中两种变量之间的比值是否一定即可.
(2)先求出1次甲比乙多运多少,再求出6次甲比乙多运多少即可.
【解答】解:(1)甲:6(一定),是比值一定,所以甲车的运货量与运货次数成正比例关系.
乙:4(一定),是比值一定,所以乙车的运货量与运货次数成正比例关系.
(2)18÷3﹣12÷3
=6﹣4
=2(吨)
2×6=12(吨)
答:甲、乙两车各运货6次,运货量相差12吨.
【点评】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值.并且知道正比例关系的图象是经过原点的一条射线.
32.判断下面各题中的两种量是否成比例?成什么比例?为什么?
(1)小麦的出粉率一定,小麦的总重量和出粉的重量。
(2)每箱木瓜的个数一定,运来木瓜的箱数和木瓜的总个数。
(3)房间的面积一定,铺地砖的块数与每块地砖的面积。
【答案】(1)成正比例,因为出粉的重量与小麦的重量的商一定;
(2)成正比例,因为木瓜的总个数与运来木瓜的箱数的商一定;
(3)成反比例,因为铺地砖的块数与每块地砖的面积的乘积一定。
【分析】两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例。据此判断。
【解答】解:(1)小麦的出粉率=出粉的重量÷小麦的重量×100%,小麦的出粉率一定时,小麦的总重量和出粉的重量成正比例;
(2)木瓜的总个数÷运来木瓜的箱数=每箱木瓜的个数,每箱木瓜的个数一定时,运来木瓜的箱数和木瓜的总个数成正比例;
(3)房间的面积=铺地砖的块数×每块地砖的面积,房间的面积一定时,铺地砖的块数与每块地砖的面积成反比例。
【点评】辨识两种相关联的量成正比例还是成反比例,就看这两种量的比值一定还是乘积一定。
33.把相同体积的水倒入底面积不同的杯子.
水的高度/cm 30 20 15 10 5 …
杯子的底面积/cm2 10 15 20 30 60 …
水的高度和杯子的底面积成反比例吗?为什么?
【答案】见试题解答内容
【分析】根据水的体积=杯子的底面积×水面的高度,列式计算,通过计算可得:水的体积一定,也就是水的高度和杯子的底面积的乘积一定,所以杯子的底面积和水的高度是成反比例的量,据此即可得解.
【解答】解:水的高度和杯子的底面积成反比例.
因为30×10=300(立方厘米)
20×15=300(立方厘米)
15×20=300(立方厘米)
10×30=300(立方厘米)
5×60=300(立方厘米)
通过计算可得:水的体积一定,也就是水的高度和杯子的底面积的乘积一定,所以杯子的底面积和水的高度成反比例.
【点评】此题主要考查反比例的意义和圆柱的体积公式的灵活应用.
34.配制一种盐水,水的质量总是比盐水的质量少15%,盐的质量与盐水的质量成正比例吗?
【答案】成正比例。
【分析】判断两种量成正比例还是成反比例时,关键看这两种相关联的量中相对应的两个数是比值一定还是乘积一定。如果比值一定,就成正比例;如果乘积一定,就成反比例;如果比值和乘积都不是定量,就不成比例。
【解答】解:(盐水的质量﹣水的质量)÷盐水的质量=盐的质量÷盐水的质量=15%,盐的质量与盐水的质量是两个相关联的量,且它们的比值一定,所以成正比例。
【点评】此题考查了辨识成正比例的量与成反比例的量,要求学生掌握。
35.某厂要生产一批豆浆机,平均每天产量和所需时间如表。
平均每天产量/台 200 300 500
所需时间/天 75 50 30
(1)平均每天产量和所需时间成 反 比例。
(2)现要在20天内完成生产任务,平均每天产量至少要达到多少台?
【答案】(1)反;(2)750。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;
(2)因为平均每天产量和所需时间成反比例,总台数不变,用总台数除以需要的天数即可解答。
【解答】解:(1)因为200×75=15000
300×50=15000
500×30=15000
所以平均每天产量×所需时间=15000(一定),乘积一定,所以平均每天产量和所需时间成反比例;
(2)15000÷20=750(台)
答:平均每天产量至少要达到750台。
故答案为:反。
【点评】熟练掌握判断两个相关联的量之间成什么比例的方法以及求平均数的方法是解题的关键。
36.妈妈买来一袋橡皮泥,平平全部用来捏大小相同的圆锥,正好没有剩余.圆锥的个数与每个圆锥所用橡皮泥的体积是否成反比例?为什么?
【答案】见试题解答内容
【分析】由于所捏的圆锥的大小相同,因此,每个圆锥所用的橡皮泥是相同的.每个圆锥用的橡皮泥×圆锥的个数=妈妈买来一袋橡皮泥(一定).根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就是成反比例的量,它们的关系是反比例关系,在这里,每个圆锥用的橡皮泥×圆锥的个数成反比例.
【解答】解:圆锥的个数与每个圆锥所用橡皮泥的体积是成反比例
理由:每个圆锥用的橡皮泥×圆锥的个数=妈妈买来一袋橡皮泥(一定)
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
37.某童车厂装配一批童车,每天装配的数量和需要的时间如表。
每天装配的数量/辆 60 90 120 180 360 …
时间/天 60 40 30 20 10 …
(1)判断每天装配的数量和时间是否成反比例,并说明理由。
(2)如果每天装配200辆,多少天可以装配完这批童车?
【答案】(1)成反比例;因为60×60=90×40=120×30=180×20=360×10=定值,所以每天装配的数量和时间成反比例;
(2)18天。
【分析】两个相关联的量的乘积不变时,这两个量成反比例关系,据此解答即可。
【解答】解:(1)每天装配的数量和时间成反比例。
因为60×60=90×40=120×30=180×20=360×10=定值,所以每天装配的数量和时间成反比例。
(2)60×60÷200
=3600÷200
=18(天)
答:如果每天装配200辆,18天可以装配完这批童车。
【点评】熟练掌握反比例关系的判断,是解答此题的关键。
38.科技小组制作了一个弹簧秤,弹簧的长度是8厘米。经验证,弹簧的长度与所挂钩码的质量存在如下关系:
弹簧长度/cm 8 9 10 11 ……
钩码质量/kg 0 2 4 6 ……
(1)钩码的质量和弹簧伸长的长度成什么比例关系?
(2)小亮用科技小组制作的这个弹簧秤称一个物体,弹簧的长度是14.8cm,这个物体的质量是多少千克?(用比例知识解答)
【答案】(1)正比例关系;(2)13.6千克。
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
(2)设这个物体的质量是x千克,由(1)可知,弹簧伸长的长度与钩码的质量成正比例关系,据此用弹簧的长度减去弹簧原来的长度与x的比等于0.5,据此列式解答即可。
【解答】解:(1)当弹簧的长度是8厘米时,钩码质量是0kg;
当弹簧的长度是9厘米时,钩码质量是2kg,即弹簧伸长(9﹣8)厘米;
当弹簧的长度是10厘米时,钩码质量是4kg,即弹簧伸长(10﹣8)厘米;
当弹簧的长度是11厘米时,钩码质量是6kg,即弹簧伸长(11﹣8)厘米;
......
(9﹣8):2=0.5
(10﹣8):4=0.5
(11﹣8):6=0.5
......
弹簧伸长的长度:钩码的质量=0.5(一定),商一定,所以钩码的质量和弹簧伸长的长度成正比例关系。
(2)设这个物体的质量是x千克。
(14.8﹣8):x=0.5
0.5x=6.8
x=13.6
答:这个物体的质量是13.6千克。
【点评】熟练掌握判断两个相关联的量之间成什么比例的方法以及利用正比例解题的方法是解题的关键。
39.判断下面每题中的两种量是不是成正比例,并说明理由.
(1)小新跳高的高度和他的身高.
(2)长方形的宽一定,它的面积和长.
(3)小麦每公顷产量一定,小麦的公顷数和总产量.
【答案】见试题解答内容
【分析】判定两种量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定,就成反比例.
【解答】解:(1)因为小新跳高的高度和他的身高的比值不是一定的,
所以小新跳高的高度和他的身高不成正比例;
(2)因为长方形的面积=长×宽,
所以长方形的面积÷长=宽(一定),
即长方形的面积与长的比值一定,
符合正比例的意义,
所以一个长方形的宽一定,它的面积和长成正比例;
(3)种小麦的面积和总产量是两种相关联的量,它们与每公顷小麦产量有下面的关系:
总产量:小麦的公顷数=每公顷小麦产量(一定);
已知每公顷小麦产量一定,也就是总产量与种小麦的公顷数的比值一定,所以种小麦的公顷数和总产量成正比例.
【点评】此题属于根据正、反比例的意义,判断两种相关联的成正比例还是成反比例,就看是对应的比值一定,还是对应的乘积一定,再做出解答.
40.小牛和大牛吃肥肉,原来小牛和大牛吃的肉块数之比为2:5,后来小牛又吃了5块,大牛也又吃了2块,此时小牛和大牛吃的肉块数之比为5:9,求原来两人各自吃了多少块肥肉?
【答案】小牛原来吃10块,大牛原来吃25块。
【分析】设原来小牛吃了2x块肥肉,大牛吃5x块肥肉,根据等量关系:(原来小牛吃的块数+5块):(原来大牛吃的块数+2块)=5:9,列方程解答即可。
【解答】解:设原来小牛吃了2x块肥肉,大牛吃5x块肥肉
(2x+5):(5x+2)=5:9
25x+10=18x+45
x=5
5×2=10(块)
5×5=25(块)
答:小牛原来吃10块,大牛原来吃25块。
【点评】本题主要考查了比例的应用,关键是根据等量关系:(原来小牛吃的块数+5块):(原来大牛吃的块数+2块)=5:9。
41.新冠肺炎疫情期间,口罩需求量大幅上升。某工厂接到任务紧急生产一批口罩,下面是每时生产口罩的数量与完成任务总共需要的时间的关系。
每时生产口罩的数量/万只 2 3 4 6
时间/时 72 48 36 24
(1)每时生产口罩的数量与时间有什么关系?(1分)
(2)如果每时生产8万只口罩,那么完成这项任务一共需要多少时?(4分)
【答案】(1)反比例;
(2)18。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:(1)因为每时生产口罩的数量与时间的积一定,所以每时生产口罩的数量与时间成反比例。
(2)2×72÷8=18(时)
答:完成这项任务一共需要18小时。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
42.用一些纸装订同样的练习本,每本用纸的张数和装订的本数如表。
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40
30
25
(1)将如表补充完整。
(2)每本用纸张数和装订本数是否成反比例关系?为什么?
(3)如果用这些纸装订成50本练习本(每本用纸张数相同),每本用纸多少张?
【答案】(1)30;25;
(2)因为8×75=10×60=15×40=20×30=24×25=定值,所以每本用纸张数和装订本数成反比例关系;
(3)12张。
【分析】(1)根据积都是600,用600除以20和24即可;
(2)判断练习本每本的页数和装订的本数之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
(3)用600除以50即可。
【解答】解:(1)
每本用纸张数/张 8 10 15 20 24
装订本数/本 75 60 40 30 25
(2)因为8×75=10×60=15×40=20×30=24×25=定值,所以每本用纸张数和装订本数成反比例关系。
(3)10×60÷50
=600÷50
=12(张)
答:每本用纸12张。
故答案为:30;25。
【点评】根据反比例的定义进行判断即可。
43.如图图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)实验小学食堂用煤的天数和用煤量是否成正比例?
(2)根据图象判断,食堂5天要用煤多少吨?2.4吨煤可以用多少天?
【答案】见试题解答内容
【分析】(1)用煤的天数和用量是两个相关联的量,用总煤量除以用煤天数就是每天的用煤量,即用煤总量÷用煤天数=每天用煤量.如果每天的用煤量一定,煤的天数和用煤量成正比例.
(2)表示5天的纵与表示用煤量的直线的交点即表示5天的用煤量,即1.5吨;表示用煤量2.4吨的横轴与表示用煤量的直线的交点即表示用煤的天数,即2.4吨煤可以有8天.
【解答】解:(1)0.3÷1=0.3(吨)
0.6÷2=0.3(吨)
0.9÷3=0.3(吨)
……
每天的用煤量一定
即用煤总量÷用煤天数=每天用煤量(一定)
答:实验小学食堂用煤的天数和用煤量成正比例.
(2)答:食堂5天要用煤1.5吨,2.4吨煤可以用8天.
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
44.某工厂有一批煤,每天烧煤的质量和可烧的时间关系如下表。
每天烧煤的质量/吨 0 3 6 9 15 20 …
可烧的时间/天 0 30 15 10 6 4.5 …
(1)判断每天烧煤的质量和可烧的时间是不是成反比例,并说明理由。
(2)如果该工厂平均每天烧煤的质量是5吨,那么这批煤可烧多少天?
【答案】(1)3×30=6×15=9×10=15×6=20×4.5=90
每天烧煤的质量和可烧的时间的乘积一定,所以每天烧煤的质量和可烧的时间成反比例。
(2)18天。
【分析】(1)根据每天烧煤的质量和可烧的时间的乘积判断。
(2)用这批煤的总质量除以每天烧煤的质量就是烧的天数。
【解答】解:(1)3×30=6×15=9×10=15×6=20×4.5=90
每天烧煤的质量和可烧的时间的乘积一定,所以每天烧煤的质量和可烧的时间成反比例。
(2)30×3÷5=18(天)
答:这批煤可烧18天。
【点评】本题考查了成反比例关系的判定及根据成反比例关系解决问题,关键是对题目中数量关系的分析。
45.
时间/时 1 2 3 4 5 6 …
路程/千米 90 …
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 正 比例,理由是 路程÷时间=速度(一定) .
③利用图象估计一下,2.5时行 225 千米,行675千米需要 7.5 小时.
【答案】见试题解答内容
【分析】①1小时行驶90千米,2小时行驶2个90千米,即180千米;3小时行3个90千米,即270千米;4小时行4个90千米,即360千米;5小时行5个90千米,即450千米;6小时行6个90千米,即540千米……然后填表,并在图中描出时间与路程对应的点,并这些点按顺序连起来.
②在这里速度一定,根据路程、速度、时间三者之间的关系,路程÷时间=速度(一定),再根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量,由此即可判定时间和路程成正比例.
③根据表示时间、路程的拆线统计图即可估计2.5小时所行的路程、行675千米年需要的时间.
【解答】解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时 1 2 3 4 5 6 …
路程/千米 90 180 270 360 450 540 …
②时间和路程成 正比例,理由是 路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行 225千米,行675千米需要 7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
【点评】此主要是考查正、反比例的辨别,关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
46.王老师准备用72元钱去买笔记本.如果每本价格是2元,能买多少本?如果每本价格是3元、4元或6元呢?
每本价格/元 2 3 4 6
数量/本 36
24
18
12
观察上表,你有什么发现?
【答案】见试题解答内容
【分析】根据数量=总价÷单价,分别用72元除以2元、3元、4元和6元求出可以购买的本数,填入表格,再根据总价一定,单价与数量的乘积一定,它们乘反比例关系求解即可.
【解答】解:72÷2=36(本)
72÷3=24(本)
72÷4=18(本)
72÷6=12(本)
表格如下:
每本价格/元 2 3 4 6
数量/本 36 24 18 12
观察上表发现:
2×36=3×24=4×18=6×12=72
即单价×数量=总价(一定),单价和数量成反比例关系.
【点评】本题考查了总价、数量和单价之间的关系,同时考查了根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择.
47.书房的面积是16m2,刚好用了32块地砖,卧室的面积是20m2,用同样的地砖,需要多少块?
【答案】40块。
【分析】根据题意知道,地砖的面积一定,房子的面积÷地砖的块数=地砖的面积(一定),所以房子的面积与方砖的块数成正比例,由此列出比例解答即可。
【解答】解:设用同样的地砖,需要X块。
16:32=20:X
16X=640
X=40
答:用同样的地砖,需要40块。
【点评】关键是判断出房子的面积与方砖的块数成正比例,由此解决问题。
48.四名同学到超市购买练习本,先填表,再回答问题.
(1)他们都带了6元,购买了不同品种的练习本.
张华 李浩 王佟 陈刚
单价/(元/本) 0.60 1.20 1.50 2.00
购买的数量/本
10
5
4
3
他们带的钱数相同,练习本的单价和购买的数量成什么比例?为什么?
(2)他们都买单价是0.60元/本的练习本.
张华 李浩 王佟 陈刚
购买的数量/本 2 5 8 9
用去的金额/元
1.2
3
4.8
5.4
购买的练习本单价相同,购买的数量和用去的金额成什么比例?为什么?
(3)已知他们买练习本用去的金额,且每人都带了6元.
张华 李浩 王佟 陈刚
用去的金额/元 0.6 1.2 1.5 2
剩下的金额/元
5.4
4.8
4.5
4
带的金额相同,用去的金额和剩下的金额成比例吗?为什么?
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:(1)他们都带了6元,购买了不同品种的练习本.
张华 李浩 王佟 陈刚
单价/(元/本) 0.60 1.20 1.50 2.00
购买的数量/本 10 5 4 3
因为练习本的单价×购买的数量=总价(一定),即乘积一定,所以练习本的单价和购买的数量成反比例.
(2)他们都买单价是0.60元/本的练习本
张华 李浩 王佟 陈刚
购买的数量/本 2 5 8 9
用去的金额/元 1.2 3 4.8 5.4
因为,总价÷购买的数量=练习本单价(一定),即商一定,所以购买的数量和用去的金额成正比例.
(3)已知他们买练习本用去的金额,且每人都带了6元.
张华 李浩 王佟 陈刚
用去的金额/元 0.6 1.2 1.5 2
剩下的金额/元 5.4 4.8 4.5 4
因为用去的金额+剩下的金额=总价,和一定.所以用去的金额和剩下的金额不成比例.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
49.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数 20 15
12
10
需要的天数
9
12 15
18
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
【答案】见试题解答内容
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系.用字母表示是k(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系.用字母表示是x×y=k(一定).
(1)这一批电动车的数量是个定值12×15=180辆,也就是:每天组装辆数×需要的天数=180辆,据此计算填表即可.
(2)根据每天组装辆数×需要的天数=180辆(一定)可解答.
(3)根据需要的天数=180÷每天组装辆数;每天组装辆数=180÷需要的天数即可.
【解答】解:(1)15×12=180(辆)
180÷20=9(天)
180÷15=12(辆)
180÷10=18(天)
每天组装辆数 20 15 12 10
需要的天数 9 12 15 18
(2)因为每天组装辆数×需要的天数=180辆(一定),即乘积一定.所以每天组装的辆数和需要的天数成反比例.
(3)180÷30=6(天)
180÷4=45(辆)
答:每天组装30辆,需要组装6天;打算4天完成组装任务,每天需要组装45辆.
故答案为:12,9,18.
【点评】此题主要考查成反比例的量,理解成反比例的量的定义,是解决此题的关键.
50.邮局准备把一批《百科全书》打包寄给山区的小朋友。每包的本数和包数如下表。
每包的本数/本 10 20 40
包数/包 60 30 15
(1)判断每包的本数和包数是不是成反比例,并说明理由。
(2)如果打包成6包,那么每包多少本?
【答案】(1)10×60=20×30=40×15=600,每包的本数和包数的乘积一定,所以每包的本数和包数成反比例。
(2)100本。
【分析】(1)根据每包的本数和包数的乘积一定,确定每包的本数和包数成反比例。
(2)根据总本数÷包数=每包的本数列除法算式解答。
【解答】解:(1)10×60=20×30=40×15=600,每包的本数和包数的乘积一定,所以每包的本数和包数成反比例。
(2)10×60÷6=100(本)
答:每包100本。
【点评】两种相关联的量,若其比值一定,两种量成正比例;若其乘积一定,两种量成反比例;若既不是比值一定也不是乘积一定,两种量不成比例。
51.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 4 9 16
所需小正方形的数量/个 216 96 54
(1)每个小正方形的面积与所需小正方形的数量成 反 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
【答案】见试题解答内容
【分析】(1)每个小正方形的面积×小正方形的数量=长方形彩纸的面积;长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)长方形彩纸的面积=36×需要小正方形个数,由此解答。
【解答】解:(1)长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)设需要多x个小正方形。
36x=216×4
36x÷36=216×4÷36
x=24
答:(1)每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)需要24个小正方形。
故答案为:反,24。
【点评】解决此题关键是根据比值一定或乘积一定,先列出比例,进而根据比例的性质先把比例式转化为乘积式来解比例得解;注意等号要对齐。
52.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出甲车行驶的路程与行驶时间同时扩大或缩小的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)由图象可知:行驶150千米的路程甲车用的时间少,所以速度较快;据此解答即可.
【解答】解:(1)两辆车子所行的路程和时间成比例,因为是一条直线,所以成正比例;
(2)由图象可知:甲行驶150km,用4.2小时,乙行驶150km,用4.4小时,
4.2<4.4,
路程相同,用的时间越少,速度较快,即甲汽车的行驶速度快些;
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的比值一定,这两种量成正比例.
53.每5m花布售价40元.
花布长度/m 1 2 3 4 5 6 7 8
总价/元 40
①把上表填完整.
②花布总价和长度是否成正比例?为什么?
【答案】见试题解答内容
【分析】①根据总价÷数量=单价,先求出每米布的售价,再根据总价=单价×数量,分别求出不同花布长度的价格即可.
②花布的长度与总价成正比例,因总价:数量=单价(一定),花布的长度与总价的比值一定,所以成正比例关系.
【解答】解:①40÷5=8(元)
1×8=8(元)
2×8=16(元)
3×8=24(元)
4×8=32(元)
6×8=48(元)
7×8=56(元)
8×8=64(元)
花布长度/m 1 2 3 4 5 6 7 8
总价/元 8 16 24 32 40 48 56 64
②花布总价和长度成正比例,因总价:数量=单价(一定),花布的长度与总价的比值一定,所以成正比例关系.
【点评】此题重点考查用正比例的意义来辨识成正比例的量.
54.王叔叔要把一张100元换成小面值的人民币.
面值/元 1 2 5 10 20 50
数量/张
(1)把表填写完整.
(2)人民币面值和张数成反比例吗?为什么?
【答案】见试题解答内容
【分析】(1)100×1=50×2=5×20=10×10=20×5=50×2=100元,据此即可解答;
(2)这个乘积表示面值与张数的积一定,即面值×张数=总值(一定);依据反比例的意义可得:面值与张数是一对相关联的量,且面值与张数的积一定,则面值与张数成反比例.
【解答】解:(1)填表如下:
面值/元 1 2 5 10 20 50
张数/张 100 50 20 10 5 2
(2)100×1=50×2=5×20=10×10=20×5=50×2=100元;这个乘积表示面值与张数的积一定,即面值×张数=总值(一定);因为面值与张数是一对相关联的量,且面值与张数的积一定,则面值与张数成反比例.
【点评】此题主要考查反比例的意义及其实际应用.
55.判断下面每题中的两种量是否成正比例关系,并说明理由.
(1)全班人数一定,出勤人数与缺勤人数;
(2)《光明日报》的单价一定,总价与数量.
【答案】见试题解答内容
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:(1)因为出勤人数+缺勤人数=全班的人数(一定)
所以全班人数一定,出勤人数与缺勤人数不成比例;
(2)因为:总量÷数量=单价(一定),
所以总价和数量成正比例.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
56.A、B两种商品的价格之比为7:2,如果它们的价格分别上涨60元后,价格之比为5:2,这两种商品原来的价格各是多少?
【答案】A原来的价格是315元,B原来的价格各是90元。
【分析】根据题意知道,A、B两种商品的价格差不会变化,由此根据“A、B两种商品的价格之比为7:2,”,知道原来A占价格差的,再根据“价格之比是5:2”知道后来A占价格差的,由此用60除以(),即可求出价格差,进而求出这两种商品原来的价格。
【解答】解:价格差是:
60÷()
=60
=225(元)
A原来的价格是:
225
=225
=315(元)
B原来的价格:315﹣225=90(元)
答:A原来的价格是315元,B原来的价格各是90元。
【点评】解答此题的关键是,根据价格差不变化,将比转化为分率,统一单位“1”,再根据基本的数量关系解决问题。
57.某物流公司将一批货物运往一家加工厂,且要一次性把所有货物全部运出,车辆的载质量与所需车辆的数量如表所示。
车辆的载质量/t 2.5 3 5 10
所需车辆的数量/辆 48 40 24 12
(1)车辆的载质量和所需车辆的数量成什么比例?如果用载质量为6t的车来运,那么一共需要多少辆?
(2)如果用15辆车来运,那么每辆车要运多少吨?
【答案】(1)反比例;20辆;(2)8吨。
【分析】(1)由统计表中的数量可以看出,车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例;运用总重量除以6就是运用卡车的辆数;
(2)运用总重量除以卡车的量数15就是每辆卡车运多少吨。
【解答】解:(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例。
120÷6=20(辆)
答:车辆的载质量和所需车辆的数量成反比例,一共需要20辆。
(2)120÷15=8(吨)
答:每辆卡车运8吨。
【点评】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题.同时考查了学生理解分析问题的能力。
58.下图表示一根水管不停地向水箱内注水时,水箱内水的体积的变化情况.
(1)水箱内水的体积与注水的时间成正比例吗?为什么?
(2)利用图象估一估,10分能注水多少升?注水45升需要多少分?再实际计算一下.
【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出水箱内水的体积与注水的时间(或缩小)的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)根据折线统计图可知,注水时间10分钟时,统计表中对应的水的体积为20升,即注水10分钟时水箱内的水的体积为20升,同理如果水要达到45升,需要注水22.5分钟.
【解答】解:(1)水箱内水的体积与注水的时间成正比例,因为水箱内水的体积与注水的时间的比值一定,且对应在一条直线上;
(2)45÷(10÷5)=22.5(分),
由图象可知10分能注水20升;注水45升需要22.5分.
【点评】此题考查借助直观的图象,辨识两种相关联的量成什么比例,只要图象是一条直线的,就成正比例;图象是一条曲线的,就成反比例;再根据成什么比例解决其它的问题.
59.一个平行四边形的面积是24m2,用x和y表示它的底和高.x与y成什么比例关系?如果把它们的关系用图象表示出来,那么它的图象是一条直线吗?
【答案】见试题解答内容
【分析】根据平行四边形的面积=底×高,即xy=24,可判断底和高的关系;再根据它们的关系判断出图象的形状.
【解答】解:因为xy=24,是乘积一定,所以y与x成反比例关系;
如果把它们的关系用图象表示出来,那么它的图象是一条曲线.
答:x与y成反比例关系,如果把它们的关系用图象表示出来,那么它的图象不是一条直线.
【点评】此题考查了两个量成何比例的方法,即如果两个量的比值一定,则这两个量成正比例,如果两个量的乘积一定,这两个量就成反比例.
60.“六一”那天,芳芳和小朋友们一起骑车去动物园玩.下面的图象表示的是她骑车的路程和时间的关系.
(1)芳芳骑车行驶的路程和时间成正比例吗?为什么?
(2)看图估计,行2.5千米大约用多少分钟?
【答案】见试题解答内容
【分析】(1)根据折线统计图可知,芳芳骑车行驶的路程和时间成正比例,因为速度一定,路程与时间成正比;
(2)芳芳行2.5千米时大约用了30÷2=15分钟.
【解答】解:(1)芳芳骑车行驶的路程和时间成正比例,因为速度一定,路程与时间成正比
