2025年中考数学课件:专项二 概率统计题(共38张PPT)
文档属性
| 名称 | 2025年中考数学课件:专项二 概率统计题(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 08:48:54 | ||
图片预览










文档简介
(共38张PPT)
第一部分 专项突破
基础·中档专项
专项二 概率统计题
统计与概率是初中数学的主要内容之一,是江西历年中考的热点题型,常考类
型有2种:①统计图表信息类;②概率类.
类型1 统计图表信息类
【解题策略】明确各统计图的特征和作用,通过对统计图表中的相关信息进行
分析、观察、猜想、抽象、概括,从中获取解题信息和思路、方法,然后再进行推
理、探究、发现和计算.同时要注意理解平均数、众数、中位数、方差等统计量的
意义,并能正确计算.
. .
. .
例1 [2024·南昌模拟] 为获取中学生对春节习俗的了解情况,某中学从八、九年级
学生中分别随机抽取了20名学生进行测试(满分100分),并对数据(成绩,单位:
分)进行整理、描述和分析.部分信息如下:
八年级学生成绩的统计表和扇形统计图如下:
统计表
等级 成绩 分 人数
A 2
B
C 6
D
60分以下 2
八年级学生的成绩中C等级的数据分别是:72,75,77,74,75,78.
九年级学生成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)如下:
平均数 中位数 众数 优秀率
80 80 77
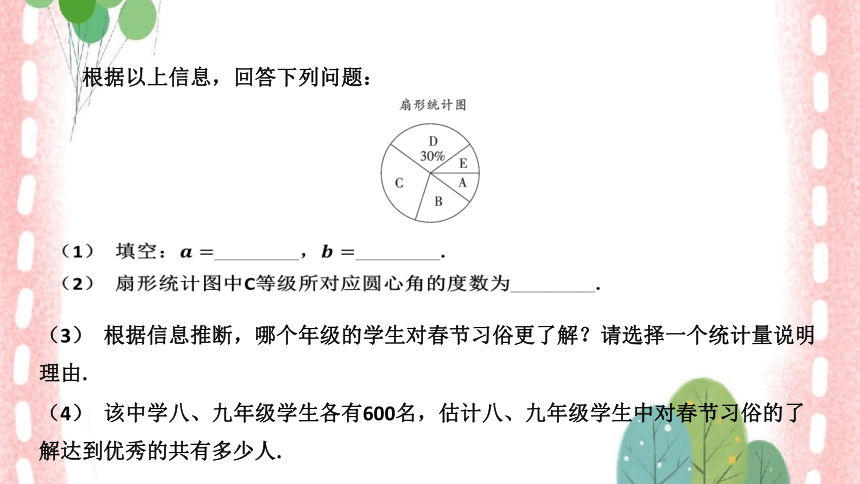
根据以上信息,回答下列问题:
(1) 填空:________, ________.
(2) 扇形统计图中C等级所对应圆心角的度数为________.
(3) 根据信息推断,哪个年级的学生对春节习俗更了解?请选择一个统计量说明
理由.
(4) 该中学八、九年级学生各有600名,估计八、九年级学生中对春节习俗的了
解达到优秀的共有多少人.
【自主解答】
(1) 填空:___, ___.
4
6
(2) 扇形统计图中C等级所对应圆心角的度数为______.
(3) 根据信息推断,哪个年级的学生对春节习俗更了解?请
选择一个统计量说明理由.
解:九年级的学生对春节习俗更了解.
理由: 八年级学生的优秀率是, ,
九年级的学生对春节习俗更了解.
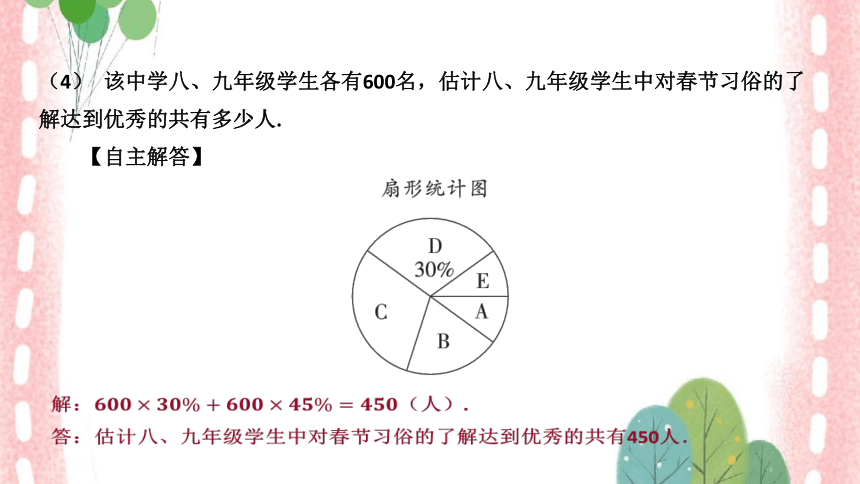
(4) 该中学八、九年级学生各有600名,估计八、九年级学生中对春节习俗的了
解达到优秀的共有多少人.
【自主解答】
解: (人).
答:估计八、九年级学生中对春节习俗的了解达到优秀的共有450人.
类型2 概率类
【解题策略】初中阶段的概率问题大多是等可能概型,求某事件 发生的概率
的公式为,因此找出试验中事件发生的总次数和事件出现的次数 是
解题的关键,解题时一般采用画树状图或列表的方法.
. .
. .
例2 [2024·九江柴桑区二模] 消防教育进校园,消防安全记心间.为切实提升广大
师生的自护自救能力,某校组织全体师生开展了消防演练.为了将演练活动做实做
细,学校提前制订了消防演练活动方案,并召开了相关专题会议,对各班撤离路线
和各岗位值守老师的职责做了明确的要求,同时在各楼层通道等关键位置设置了疏
散引导员,以保障秩序稳定,避免发生踩踏等安全事故.该校决定在七年级的甲、
乙、丙、丁4位老师中随机选取2位作为疏散引导员,其中甲、乙、丙是男老师,丁
是女老师.
(1) “选取的2位疏散引导员都是女老师”是________(填“不可能”“必然”或“随
机” )事件.
(2) 请用画树状图法或列表法求被选到的2位老师是一男一女的概率.
【自主解答】
(1) “选取的2位疏散引导员都是女老师”是________(填“不可能”“必然”或“随
机” )事件.
不可能
(2) 请用画树状图法或列表法求被选到的2位老师是一男一女的概率.
【自主解答】
解:画树状图如下:
一共有12种等可能的结果,其中被选到的2位老师是一男一女的结果有6种, 被选
到的2位老师是一男一女的概率为 .
类型1 统计图表信息类
1.[2024·江西模拟] 某次语文测试中,有一道满分为10分的语文小作文题,其评分标
准为:
A.未清楚表达,评为1分;
B.略有错误,评为3分;
C.正确阐明观点,评为5分;
D.简明地表达观点,评为8分;
E.完整、精准地表达出观点,评为满分10分.
. .
. .
为了解九年级学生语文小作文的得分情况,该校对九年级学
生以20人为一组进行了随机分组,并从中随机抽取了3个小组
学生的答卷进行统计分析,过程如下:
【整理与描述】
(1) 请补全第1小组得分条形统计图.
(2) 在第2小组得分扇形统计图中,求“8分”这一项所对应的圆心角度数.
【分析与估计】
平均数/分 众数/分 中位数/分
第1小组 7.5 8
第2小组 1 3
第3小组 5.9 5
(3) 由上表填空:________,________, ________;
(4) 若该校九年级有600名学生,请你估计该校九年级学生在本次测试中小作
文得分为10分的人数.
(1) 请补全第1小组得分条形统计图.
解:补全的条形统计图如图.
(2) 在第2小组得分扇形统计图中,求“8分”这一项所对应的圆心角度数.
解: .
【分析与估计】
平均数/分 众数/分 中位数/分
第1小组 7.5 8
第2小组 1 3
第3小组 5.9 5
(3) 由上表填空:____,_____, ___;
10
3.35
5
[解析] 第1小组得分出现次数最多的是10分,共出现了8次,因此众数 .
第2小组得分的平均数
.
第3小组得分的中位数 .
(4) 若该校九年级有600名学生,请你估计该校九年级学生在本次测试中小作文
得分为10分的人数.
解: (人).
答:估计该校九年级学生在测试中小作文得分为10分的人数为110.
2.[2024·高安模拟] 4月24日是中国航天日,某校开展了“逐梦太空”航空航天知识问
答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取
了20名学生的成绩进行统计分析(6分及6分以上为合格,9分及9分以上为优秀),
并绘制成如下统计图表:
七年级 八年级
平均数 7.55
中位数 8
众数 7
合格率
根据上述信息,解答下列问题:
(1) 学生成绩统计表中, _______,
________, ________.
(2) 求七年级学生成绩的平均数 .
(3) 根据以上数据,你认为该校七年级和八年级中,哪个年级的学生对航空航天
知识掌握得更好?请说明理由.
(1) 学生成绩统计表中,___, ____,
______.
8
7.5
(2) 求七年级学生成绩的平均数 .
解:七年级学生成绩的平均数
(分).
(3) 根据以上数据,你认为该校七年级和八年级中,哪个年级的学生对航空航天
知识掌握得更好?请说明理由.
解:七年级的学生对航空航天知识掌握得更好.理由:因为两个年级的平均数相同,
但七年级的中位数和众数均高于八年级,所以七年级的学生对航空航天知识掌握得
更好.
类型2 概率类
3.第八届丝博会于2024年9月20日至24日在西安国际会展中心举办.本届丝博会以“深
化互联互通·拓展经贸合作”为主题.在丝博会举办之际,某机构计划向全市中小学生
招募“丝博小记者”.某校现有甲、乙两位男生和丙、丁两位女生参加小记者竞选.
(1) 若先从这四位竞选者中随机选出一位小记者,则选到男生的概率是________;
(2) 若从这四位竞选者中随机选出两位小记者,请用列表或画树状图的方法求出
两位女生同时当选的概率.
. .
. .
(1) 若先从这四位竞选者中随机选出一位小记者,则选到男生的概率是_ _;
[解析] 甲、乙两位男生和丙、丁两位女生参加小记者竞选,
从这四位竞选者中随机选出一位小记者,选到男生的概率是 .
故答案为 .
(2) 若从这四位竞选者中随机选出两位小记者,请用列表或画树状图的方法求出
两位女生同时当选的概率.
解:画树状图如下:
由图可知,共有12种等可能的结果,其中两位女生同时当选的结果有2种,
两位女生同时当选的概率是 .
4.[2024·赣州二模] 在一次摸球试验中,把只有颜色不同的红色小球和白色小球,随
机放在甲、乙两个不透明的袋子里,已知甲袋的4个小球中只有一个白色球,乙袋
的3个小球中只有一个红色球.
(1) “从甲袋中摸出的一个球是白色球”是________(填“随机”“必然”或“不可能” )
事件.
(2) 请用列表法或画树状图法,求出“从两个袋子中各摸出一个球,两个球都是
红色球”的概率.
(1) “从甲袋中摸出的一个球是白色球”是______(填“随机”“必然”或“不可能” )事件.
随机
[解析] 甲袋的4个小球中只有一个白色球,
“从甲袋中摸出的一个球是白色球”是随机事件.故答案为:随机.
(2) 请用列表法或画树状图法,求出“从两个袋子中各摸出一个球,两个球都是
红色球”的概率.
解:可画树状图如下:
共有12种等可能的结果,其中摸到的两个球都是红色球的结果有3种,
(两个球都是红色球) .
5.人类的性别是由一对性染色体 决定的,当
染色体为时是女性,当染色体为 时是男性.下
图为一对夫妻的性染色体遗传图谱.
(1) 这对夫妻“第一胎为男孩”是________
(填“不可能”“必然”或“随机”)事件,“第一胎为
女孩”的概率是________.
(2) 这对夫妻计划生两个小孩,请用列表或画树状图的方法求出两个小孩是“一
男一女”的概率.
(1) 这对夫妻“第一胎为男孩”是______(填“不可能”“必然”或“随机”)事件,“第
一胎为女孩”的概率是__.
随机
(2) 这对夫妻计划生两个小孩,请用列表或画
树状图的方法求出两个小孩是“一男一女”的概率.
解:画树状图如下:
共有4种等可能的结果,其中一男一女的结果有2种,
(两个小孩是“一男一女”) .
6.通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.一次化学课上,
学生用酚酞溶液检测四瓶标签被污染无法分辨的无色溶液的酸碱性.已知四瓶溶液
分别是盐酸(呈酸性),硝酸钾溶液(呈中性), 氢氧化钠溶
液(呈碱性), 氢氧化钾溶液(呈碱性).
(1) 小周将酚酞溶液随机滴入一种溶液里,结果变红色的概率是多少?
(2) 小周任选两瓶溶液,同时滴入酚酞溶液进行检测,请你用列表或画树状图的
方法,求两瓶溶液恰好都变红色的概率.
(1) 小周将酚酞溶液随机滴入一种溶液里,结果变红色的概率是多少?
解: 酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色,
小周将酚酞溶液随机滴入其中一瓶溶液里,盐酸和硝酸钾溶液不变色,氢氧化钠
溶液和氢氧化钾溶液变红色,
结果变红色的概率为 .
(2) 小周任选两瓶溶液,同时滴入酚酞溶液进行检测,请你用列表或画树状图的
方法,求两瓶溶液恰好都变红色的概率.
解:列表如下:
A B C D
A -
B -
C -
D -
由表知,共有12种等可能出现的结果,其中两瓶溶液恰好都变红色的结果共2种,
即, ,
两瓶溶液恰好都变红色的概率 .
谢 谢
第一部分 专项突破
基础·中档专项
专项二 概率统计题
统计与概率是初中数学的主要内容之一,是江西历年中考的热点题型,常考类
型有2种:①统计图表信息类;②概率类.
类型1 统计图表信息类
【解题策略】明确各统计图的特征和作用,通过对统计图表中的相关信息进行
分析、观察、猜想、抽象、概括,从中获取解题信息和思路、方法,然后再进行推
理、探究、发现和计算.同时要注意理解平均数、众数、中位数、方差等统计量的
意义,并能正确计算.
. .
. .
例1 [2024·南昌模拟] 为获取中学生对春节习俗的了解情况,某中学从八、九年级
学生中分别随机抽取了20名学生进行测试(满分100分),并对数据(成绩,单位:
分)进行整理、描述和分析.部分信息如下:
八年级学生成绩的统计表和扇形统计图如下:
统计表
等级 成绩 分 人数
A 2
B
C 6
D
60分以下 2
八年级学生的成绩中C等级的数据分别是:72,75,77,74,75,78.
九年级学生成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)如下:
平均数 中位数 众数 优秀率
80 80 77
根据以上信息,回答下列问题:
(1) 填空:________, ________.
(2) 扇形统计图中C等级所对应圆心角的度数为________.
(3) 根据信息推断,哪个年级的学生对春节习俗更了解?请选择一个统计量说明
理由.
(4) 该中学八、九年级学生各有600名,估计八、九年级学生中对春节习俗的了
解达到优秀的共有多少人.
【自主解答】
(1) 填空:___, ___.
4
6
(2) 扇形统计图中C等级所对应圆心角的度数为______.
(3) 根据信息推断,哪个年级的学生对春节习俗更了解?请
选择一个统计量说明理由.
解:九年级的学生对春节习俗更了解.
理由: 八年级学生的优秀率是, ,
九年级的学生对春节习俗更了解.
(4) 该中学八、九年级学生各有600名,估计八、九年级学生中对春节习俗的了
解达到优秀的共有多少人.
【自主解答】
解: (人).
答:估计八、九年级学生中对春节习俗的了解达到优秀的共有450人.
类型2 概率类
【解题策略】初中阶段的概率问题大多是等可能概型,求某事件 发生的概率
的公式为,因此找出试验中事件发生的总次数和事件出现的次数 是
解题的关键,解题时一般采用画树状图或列表的方法.
. .
. .
例2 [2024·九江柴桑区二模] 消防教育进校园,消防安全记心间.为切实提升广大
师生的自护自救能力,某校组织全体师生开展了消防演练.为了将演练活动做实做
细,学校提前制订了消防演练活动方案,并召开了相关专题会议,对各班撤离路线
和各岗位值守老师的职责做了明确的要求,同时在各楼层通道等关键位置设置了疏
散引导员,以保障秩序稳定,避免发生踩踏等安全事故.该校决定在七年级的甲、
乙、丙、丁4位老师中随机选取2位作为疏散引导员,其中甲、乙、丙是男老师,丁
是女老师.
(1) “选取的2位疏散引导员都是女老师”是________(填“不可能”“必然”或“随
机” )事件.
(2) 请用画树状图法或列表法求被选到的2位老师是一男一女的概率.
【自主解答】
(1) “选取的2位疏散引导员都是女老师”是________(填“不可能”“必然”或“随
机” )事件.
不可能
(2) 请用画树状图法或列表法求被选到的2位老师是一男一女的概率.
【自主解答】
解:画树状图如下:
一共有12种等可能的结果,其中被选到的2位老师是一男一女的结果有6种, 被选
到的2位老师是一男一女的概率为 .
类型1 统计图表信息类
1.[2024·江西模拟] 某次语文测试中,有一道满分为10分的语文小作文题,其评分标
准为:
A.未清楚表达,评为1分;
B.略有错误,评为3分;
C.正确阐明观点,评为5分;
D.简明地表达观点,评为8分;
E.完整、精准地表达出观点,评为满分10分.
. .
. .
为了解九年级学生语文小作文的得分情况,该校对九年级学
生以20人为一组进行了随机分组,并从中随机抽取了3个小组
学生的答卷进行统计分析,过程如下:
【整理与描述】
(1) 请补全第1小组得分条形统计图.
(2) 在第2小组得分扇形统计图中,求“8分”这一项所对应的圆心角度数.
【分析与估计】
平均数/分 众数/分 中位数/分
第1小组 7.5 8
第2小组 1 3
第3小组 5.9 5
(3) 由上表填空:________,________, ________;
(4) 若该校九年级有600名学生,请你估计该校九年级学生在本次测试中小作
文得分为10分的人数.
(1) 请补全第1小组得分条形统计图.
解:补全的条形统计图如图.
(2) 在第2小组得分扇形统计图中,求“8分”这一项所对应的圆心角度数.
解: .
【分析与估计】
平均数/分 众数/分 中位数/分
第1小组 7.5 8
第2小组 1 3
第3小组 5.9 5
(3) 由上表填空:____,_____, ___;
10
3.35
5
[解析] 第1小组得分出现次数最多的是10分,共出现了8次,因此众数 .
第2小组得分的平均数
.
第3小组得分的中位数 .
(4) 若该校九年级有600名学生,请你估计该校九年级学生在本次测试中小作文
得分为10分的人数.
解: (人).
答:估计该校九年级学生在测试中小作文得分为10分的人数为110.
2.[2024·高安模拟] 4月24日是中国航天日,某校开展了“逐梦太空”航空航天知识问
答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取
了20名学生的成绩进行统计分析(6分及6分以上为合格,9分及9分以上为优秀),
并绘制成如下统计图表:
七年级 八年级
平均数 7.55
中位数 8
众数 7
合格率
根据上述信息,解答下列问题:
(1) 学生成绩统计表中, _______,
________, ________.
(2) 求七年级学生成绩的平均数 .
(3) 根据以上数据,你认为该校七年级和八年级中,哪个年级的学生对航空航天
知识掌握得更好?请说明理由.
(1) 学生成绩统计表中,___, ____,
______.
8
7.5
(2) 求七年级学生成绩的平均数 .
解:七年级学生成绩的平均数
(分).
(3) 根据以上数据,你认为该校七年级和八年级中,哪个年级的学生对航空航天
知识掌握得更好?请说明理由.
解:七年级的学生对航空航天知识掌握得更好.理由:因为两个年级的平均数相同,
但七年级的中位数和众数均高于八年级,所以七年级的学生对航空航天知识掌握得
更好.
类型2 概率类
3.第八届丝博会于2024年9月20日至24日在西安国际会展中心举办.本届丝博会以“深
化互联互通·拓展经贸合作”为主题.在丝博会举办之际,某机构计划向全市中小学生
招募“丝博小记者”.某校现有甲、乙两位男生和丙、丁两位女生参加小记者竞选.
(1) 若先从这四位竞选者中随机选出一位小记者,则选到男生的概率是________;
(2) 若从这四位竞选者中随机选出两位小记者,请用列表或画树状图的方法求出
两位女生同时当选的概率.
. .
. .
(1) 若先从这四位竞选者中随机选出一位小记者,则选到男生的概率是_ _;
[解析] 甲、乙两位男生和丙、丁两位女生参加小记者竞选,
从这四位竞选者中随机选出一位小记者,选到男生的概率是 .
故答案为 .
(2) 若从这四位竞选者中随机选出两位小记者,请用列表或画树状图的方法求出
两位女生同时当选的概率.
解:画树状图如下:
由图可知,共有12种等可能的结果,其中两位女生同时当选的结果有2种,
两位女生同时当选的概率是 .
4.[2024·赣州二模] 在一次摸球试验中,把只有颜色不同的红色小球和白色小球,随
机放在甲、乙两个不透明的袋子里,已知甲袋的4个小球中只有一个白色球,乙袋
的3个小球中只有一个红色球.
(1) “从甲袋中摸出的一个球是白色球”是________(填“随机”“必然”或“不可能” )
事件.
(2) 请用列表法或画树状图法,求出“从两个袋子中各摸出一个球,两个球都是
红色球”的概率.
(1) “从甲袋中摸出的一个球是白色球”是______(填“随机”“必然”或“不可能” )事件.
随机
[解析] 甲袋的4个小球中只有一个白色球,
“从甲袋中摸出的一个球是白色球”是随机事件.故答案为:随机.
(2) 请用列表法或画树状图法,求出“从两个袋子中各摸出一个球,两个球都是
红色球”的概率.
解:可画树状图如下:
共有12种等可能的结果,其中摸到的两个球都是红色球的结果有3种,
(两个球都是红色球) .
5.人类的性别是由一对性染色体 决定的,当
染色体为时是女性,当染色体为 时是男性.下
图为一对夫妻的性染色体遗传图谱.
(1) 这对夫妻“第一胎为男孩”是________
(填“不可能”“必然”或“随机”)事件,“第一胎为
女孩”的概率是________.
(2) 这对夫妻计划生两个小孩,请用列表或画树状图的方法求出两个小孩是“一
男一女”的概率.
(1) 这对夫妻“第一胎为男孩”是______(填“不可能”“必然”或“随机”)事件,“第
一胎为女孩”的概率是__.
随机
(2) 这对夫妻计划生两个小孩,请用列表或画
树状图的方法求出两个小孩是“一男一女”的概率.
解:画树状图如下:
共有4种等可能的结果,其中一男一女的结果有2种,
(两个小孩是“一男一女”) .
6.通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.一次化学课上,
学生用酚酞溶液检测四瓶标签被污染无法分辨的无色溶液的酸碱性.已知四瓶溶液
分别是盐酸(呈酸性),硝酸钾溶液(呈中性), 氢氧化钠溶
液(呈碱性), 氢氧化钾溶液(呈碱性).
(1) 小周将酚酞溶液随机滴入一种溶液里,结果变红色的概率是多少?
(2) 小周任选两瓶溶液,同时滴入酚酞溶液进行检测,请你用列表或画树状图的
方法,求两瓶溶液恰好都变红色的概率.
(1) 小周将酚酞溶液随机滴入一种溶液里,结果变红色的概率是多少?
解: 酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色,
小周将酚酞溶液随机滴入其中一瓶溶液里,盐酸和硝酸钾溶液不变色,氢氧化钠
溶液和氢氧化钾溶液变红色,
结果变红色的概率为 .
(2) 小周任选两瓶溶液,同时滴入酚酞溶液进行检测,请你用列表或画树状图的
方法,求两瓶溶液恰好都变红色的概率.
解:列表如下:
A B C D
A -
B -
C -
D -
由表知,共有12种等可能出现的结果,其中两瓶溶液恰好都变红色的结果共2种,
即, ,
两瓶溶液恰好都变红色的概率 .
谢 谢
同课章节目录
