2025年中考数学课件:专项三 实物情景题(共55张PPT)
文档属性
| 名称 | 2025年中考数学课件:专项三 实物情景题(共55张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 08:50:15 | ||
图片预览








文档简介
(共55张PPT)
第一部分 专项突破
基础·中档专项
专项三 实物情景题
实物情景类应用题是江西中考的创新题型,也是必考题型.此类试题通常考查
应用意识,要求能用数学知识解决实际问题.这类试题有一个显著的特点,就是题目的
背景都来源于生活中的某个实物或情景,题型以解答题为主,试题呈现形式活泼新
颖,具有时代气息和育人价值.该类题综合性较强,属于中等难度试题,解决此类问题
通常需要构造直角三角形,灵活应用解直角三角形及相关的几何知识进行解答.常考
类型有:①三角形模型;②四边形模型;③圆模型.
类型1 三角形模型
【解题策略】解决此类问题时要了解实物图以及由实物图抽象出的几何图形,
寻找边角之间的关系,找到已知和未知之间相关联的直角三角形,因此掌握三角形
的性质和锐角三角函数的应用是解题的关键.当图形中没有直角三角形时,要通过
作高或垂线构造直角三角形.
. .
. .
例1 [2024·景德镇三模] 滕王阁,世称“西江第一楼”,
与湖南岳阳岳阳楼、湖北武汉黄鹤楼并称为“江南三
大名楼”.如图,滕王阁前有一斜坡,长为 ,
高为, .为了计算滕王阁的高度,利
(1) 求斜坡的高度 ;
(2) 求滕王阁的高度 .
(参考数据:,, ,
, .结果保留一位小数)
用测角仪在斜坡底端的点处测得塔尖点的仰角为 ,在斜坡顶端的点 处测
得塔尖点的仰角为 ,其中点,, 在同一直线上.
【自主解答】
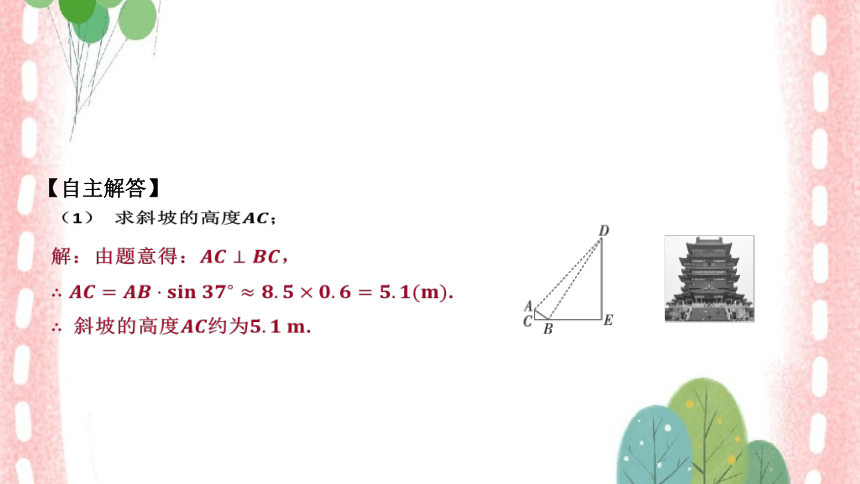
(1) 求斜坡的高度 ;
解:由题意得: ,
.
斜坡的高度约为 .
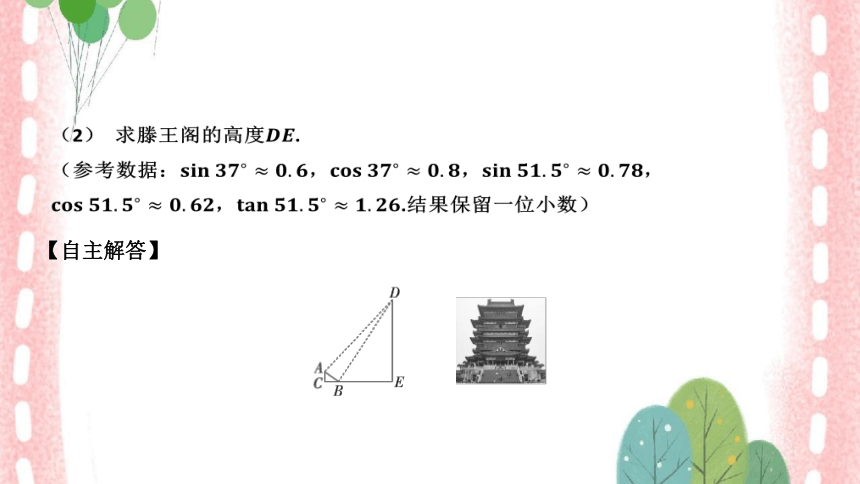
(2) 求滕王阁的高度 .
(参考数据:,, ,
, .结果保留一位小数)
【自主解答】
解:过点作,垂足为 .
由题意得:, .
在中,, ,
.
设 ,
.
在中, ,
.
在中, ,
.
,
,解得 .
.
滕王阁的高度约为 .
类型2 四边形模型
【解题策略】解决这类问题大家要善于用数学的眼光去观察实物,将实物抽象
成特殊四边形模型,再通过作辅助线,把四边形模型转化为我们熟悉的三角形模型,
利用直角三角形边角之间的关系来解答.因此掌握好特殊四边形的性质、解直角三
角形的应用是解题的关键.
. .
. .
例2 [2024·南昌模拟] 图1是某折叠资料架,图2为其侧
面示意图.已知 ,
,,,,四点分别是 ,
,,的中点,两点也分别在和 上
, 底座,垂足为 ,经测量,
,
, .
(1) 求证:四边形 为菱形.
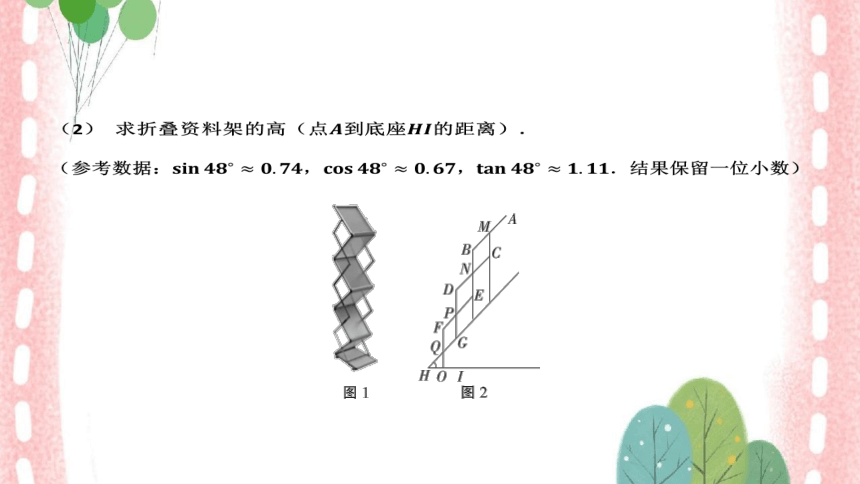
(2) 求折叠资料架的高(点到底座 的距离).
(参考数据:,, .结果保留一位小数)
【自主解答】
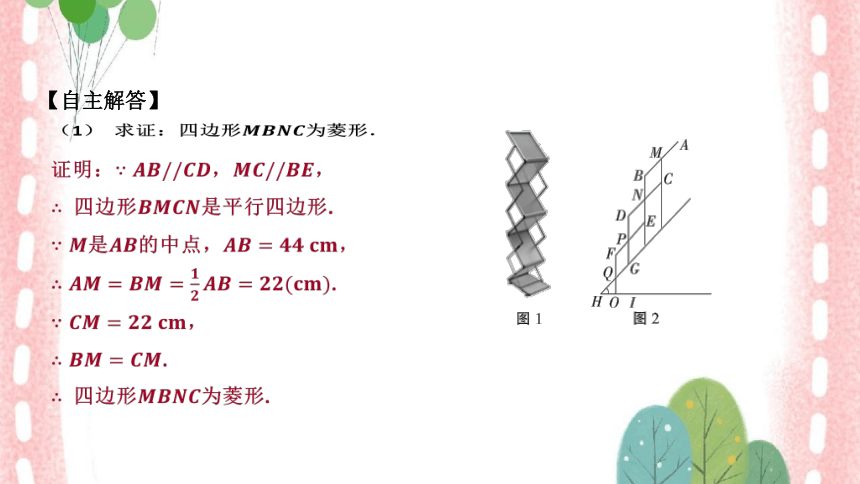
(1) 求证:四边形 为菱形.
证明:, ,
四边形 是平行四边形.
是的中点, ,
.
,
.
四边形 为菱形.
(2) 求折叠资料架的高(点到底座 的距离).
(参考数据:,, .结果保留一位小数)
【自主解答】
解:如图,过点作,交于点 .
是 的中点,
.
由题意得: ,
,
.
在中, ,
.
.
折叠资料架的高约为 .
类型3 圆模型
【解题策略】对于“圆模型”问题,题中一般会提供几何图形,解题过程中要侧
重于对几何图形本身的分析,通过作辅助线,利用圆的几何性质以及解直角三角形
的知识求解.
例3 某品牌太阳能热水器的实物图和横断面示意
图如图所示.已知真空集热管与支架 所在直
线相交于点,且,支架 与水平地面
垂直., ,
(1) 求支架的长和点 到地面的距离;
,另一支架与水平线的夹角 .
. .
. .
(2) 求热水器容器的侧面圆的半径 的长.
结果精确到.参考数据:,, ,
【自主解答】
(1) 求支架的长和点 到地面的距离;
解:如图,过点作,垂足为 .
, ,
.
, ,
.
支架的长约为,点到地面的距离为 .
(2) 求热水器容器的侧面圆的半径 的长.
结果精确到.参考数据:,, ,
【自主解答】
解:设 ,
.
, .
.
在中, ,
.
,解得 .
.
类型1 三角形模型
1.[2024·辽宁] 如图1,在水平地面上,一辆小车
用一根绕过定滑轮的绳子将物体竖直向上提
起.起始位置示意图如图2,此时测得点到
所在直线的距离, ;停止位
(1) 求 的长;
置示意图如图3,此时测得 (点,,在同一直线上,且直线 与
地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子
总长不变.
. .
. .
(2) 求物体上升的高度结果精确到 .
参考数据:,,,
(1) 求 的长;
解:在 中,
, ,
.
.
(2) 求物体上升的高度结果精确到 .
参考数据:,,,
解:在中,, ,
根据勾股定理得:
.
在中, ,
,即 ,
.
,
.
故物体上升的高度约为 .
2.屏风,是中国传统建筑物内部挡风用的一种家
具,也是一种装饰物.图1是一个四扇屏风,它能
够在室内为后面休息的人提供遮挡,它的俯视图
如图2所示,其中 ,
(1) 当 时,________ ;
(2) 若需要的长度为,应该将 的值调整为多少? 参考数据:
,,
点,,在同一条直线上, 的长为该屏风能够遮挡的长度,若
, 的值可以根据屏风不同的摆放方式而改变.
(1) 当 时,_____ ;
120
(2) 若需要的长度为,应该将 的
值调整为多少?参考数据: ,
,
解:如图,分别过点,作于点, 于
点 .
, ,
.
.
.
.
应该将 的值调整为 .
3.综合与实践
素材一:图1是某款遮阳棚,图2、图3是它的
侧面示意图,点, 为墙壁上的固定点,摇臂
绕点旋转过程中长度保持不变,遮阳棚
素材二:该地区某天不同时刻太阳光线与地面的夹角 的正切值如下.
时刻/时 12 13 14 15
角 的正切值 5 2.5 1.25 1
可自由伸缩,棚面始终保持平整, .
【问题解决】
(1) 如图2,当 时,这天12时
在点 位置摆放的绿萝刚好不被阳光照射到,
则绿萝摆放位置与墙壁的距离为________ ;
(2) 如图3,旋转摇臂,使得点离墙壁的距离为 ,为使绿萝在这天
时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?
(1) 如图2,当 时,这天12时在点 位置摆放的绿萝刚好不被阳光照
射到,则绿萝摆放位置与墙壁的距离为____ ;
1.2
(2) 如图3,旋转摇臂,使得点离墙壁的距离为 ,为使绿萝在这天
时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?
解:过点作于点,于点,则 ,
.
.
由表格可知,在 时,
角 的正切值逐渐减小,即 逐渐减小,
当14时,点 最靠近墙壁,
此时 的长度就是绿萝摆放位置与墙壁的最远距离.
在中,,即, .
.
答:绿萝摆放位置与墙壁的最远距离是 .
类型2 四边形模型
4.[2024·九江柴桑区二模] 某市要新建一座红色文化雕塑,图1是效果图,图2是雕塑
正面的大致示意图,在底座中,, ,
,雕塑主体是五边形,, ,
, , , .
(1) 的度数为________.
(2) 求点到地面的距离. 参考数据:
, ,
,
. .
. .
(1) 的度数为_____.
(2) 求点到地面的距离. 参考数据:
, ,
,
解:过点作于点,过点作于点,交 于
点,过点作于点,作于点,则 .
易知四边形和四边形 是矩形,
, .
在 中,
.
在 中,
.
, .
.
在中, .
.
故点到地面的距离约为 .
5.某数学小组用五个全等的菱形在同一平面
内拼成了一个轴对称的无人机模型,图1是
无人机模型的示意图,其中,,, 四
点在同一条直线上,菱形的边长为 .
(1) 若,,,四点在同一条直线上, ,则此时无人机模型的宽
度 ________ .
(2) 如图2,当无人机模型中的菱形被调整为正方形时,无人机模型的宽度相比
(1)中增加了多少?
结果精确到,,,, ,
,,
(1) 若,,,四点在同一条直线上, ,则此时无人机模型的宽
度 ____ .
47
(2) 如图2,当无人机模型中的菱形被调整为正方形时,无人机模型的宽度相比
(1)中增加了多少?
结果精确到,,,, ,
,,
解:当无人机模型中的菱形被调整为正方形时,如图,
过点作.由题意可知 为等腰直角三角
形,
.
, .
连接.由题意可知 ,
,
.
过点作于点,易得 .
无人机模型的宽度 .
相比(1),无人机模型的宽度增加了
.
6.某景区草地上竖立着一个如图1所示的雕塑,现
将其中两个近似大小相同的矩形框架抽象成如图2
所示的图形,矩形可由矩形绕点 旋转
得到,点在上,延长交于点.连接 ,
.
(1) 判断四边形 的形状并给予证明;
(2) 若点在水平地面上,与水平地面平行, , ,
,求点到水平地面的距离.结果精确到
参考数据:,,, ,
(1) 判断四边形 的形状并给予证明;
解:四边形 是平行四边形.
证明: 四边形 是矩形,
,, .
.
四边形是矩形, .
结合旋转易得 ,
.
由旋转得, .
又, 四边形 为平行四边形.
(2) 若点在水平地面上,与水平地面平行, , ,
,求点到水平地面的距离.结果精确到
参考数据:,,, ,
解:如图,延长交水平地面于点,连接 .
,, .
.
.
由(1)易知,.又 ,
.
由平行线的性质易知 ,
.
,
即点到水平地面的距离约为 .
类型3 圆模型
7.图1所示的是一种纸巾盒,由盒身和圆弧盖组成,
通过圆弧盖的旋转来开关纸巾盒.图2是其侧面简
化示意图,已知矩形的长 ,宽
(1) 求所在的的半径长及 所对的圆心角度数;
(2) 如图3,将圆弧盖板侧面从起始位置绕点旋转 ,求 在这个旋
转过程中扫过的面积.
参考数据:,. 取
,圆弧盖板侧面所在圆的圆心是矩形的中心,绕点 旋转开
关(所有结果保留小数点后一位).
. .
. .
(1) 求所在的的半径长及 所对的圆心角度数;
解:如图,连接,,相交于点,为矩形 的中心.
四边形 为矩形,
.
在 中,
.
的半径长 .
,
.
.
(2) 如图3,将圆弧盖板侧面 从起始位置
绕点旋转 ,求 在这个旋转过程中
扫过的面积.
解:如图, ,
扫过的面积 .
参考数据: ,
. 取
8.“南昌之星”摩天轮,是国内最高的摩天轮,位
于江西省南昌市红谷滩区红角洲赣江市民公园.
游客乘坐南昌之星摩天轮可以从高处俯瞰四周美
(1) 若摩天轮转动一周约 ,则摩天轮每分钟转________度.
(2) 若 ,则点 距离地面多少米?
(3) 游客甲从点 进入座舱之后,又有8个座舱经过,游客乙进入第8个座舱,当
甲、乙乘坐的座舱到地面的距离相等时,求他们的座舱距离地面的高度.
参考数据:,,,
景,饱览赣江两岸风光.据工作人员介绍,该摩天轮总高度为 ,转盘直径为
,设有60个座舱,游客先乘坐直升电梯到入口(入口在摩天轮距地面 的最低
点处)处等待,当座舱到达最低点 处时有序进入座舱. (结果保留小数点后一位)
(1) 若摩天轮转动一周约 ,则摩天轮每分钟转____度.
12
(2) 若 ,则点 距离地面多少米?
解:如答图1,过点作于点,过点作于点 .
,, ,
.
四边形 为矩形.
.
又 , ,
.
.
.
答:点距离地面约 .
(3) 游客甲从点 进入座舱之后,又有8个座舱经过,游客乙进入第8个座舱,当
甲、乙乘坐的座舱到地面的距离相等时,求他们的座舱距离地面的高度.
参考数据:,,,
解: 摩天轮一共有60个座舱且旋转一周为 ,
每两个座舱相隔 .
设甲乘坐的座舱为点,乙乘坐的座舱为点 ,
由题意得甲、乙两人的座舱形成的夹角 .
甲、乙两人座舱到地面的距离相等,
.
延长交于点 ,
则 .
如答图2,过点作,垂足为,过点作于点 ,
易知四边形 为矩形.
.
, .
.
.
答:甲、乙乘坐的座舱距离地面的高度约为 .
第一部分 专项突破
基础·中档专项
专项三 实物情景题
实物情景类应用题是江西中考的创新题型,也是必考题型.此类试题通常考查
应用意识,要求能用数学知识解决实际问题.这类试题有一个显著的特点,就是题目的
背景都来源于生活中的某个实物或情景,题型以解答题为主,试题呈现形式活泼新
颖,具有时代气息和育人价值.该类题综合性较强,属于中等难度试题,解决此类问题
通常需要构造直角三角形,灵活应用解直角三角形及相关的几何知识进行解答.常考
类型有:①三角形模型;②四边形模型;③圆模型.
类型1 三角形模型
【解题策略】解决此类问题时要了解实物图以及由实物图抽象出的几何图形,
寻找边角之间的关系,找到已知和未知之间相关联的直角三角形,因此掌握三角形
的性质和锐角三角函数的应用是解题的关键.当图形中没有直角三角形时,要通过
作高或垂线构造直角三角形.
. .
. .
例1 [2024·景德镇三模] 滕王阁,世称“西江第一楼”,
与湖南岳阳岳阳楼、湖北武汉黄鹤楼并称为“江南三
大名楼”.如图,滕王阁前有一斜坡,长为 ,
高为, .为了计算滕王阁的高度,利
(1) 求斜坡的高度 ;
(2) 求滕王阁的高度 .
(参考数据:,, ,
, .结果保留一位小数)
用测角仪在斜坡底端的点处测得塔尖点的仰角为 ,在斜坡顶端的点 处测
得塔尖点的仰角为 ,其中点,, 在同一直线上.
【自主解答】
(1) 求斜坡的高度 ;
解:由题意得: ,
.
斜坡的高度约为 .
(2) 求滕王阁的高度 .
(参考数据:,, ,
, .结果保留一位小数)
【自主解答】
解:过点作,垂足为 .
由题意得:, .
在中,, ,
.
设 ,
.
在中, ,
.
在中, ,
.
,
,解得 .
.
滕王阁的高度约为 .
类型2 四边形模型
【解题策略】解决这类问题大家要善于用数学的眼光去观察实物,将实物抽象
成特殊四边形模型,再通过作辅助线,把四边形模型转化为我们熟悉的三角形模型,
利用直角三角形边角之间的关系来解答.因此掌握好特殊四边形的性质、解直角三
角形的应用是解题的关键.
. .
. .
例2 [2024·南昌模拟] 图1是某折叠资料架,图2为其侧
面示意图.已知 ,
,,,,四点分别是 ,
,,的中点,两点也分别在和 上
, 底座,垂足为 ,经测量,
,
, .
(1) 求证:四边形 为菱形.
(2) 求折叠资料架的高(点到底座 的距离).
(参考数据:,, .结果保留一位小数)
【自主解答】
(1) 求证:四边形 为菱形.
证明:, ,
四边形 是平行四边形.
是的中点, ,
.
,
.
四边形 为菱形.
(2) 求折叠资料架的高(点到底座 的距离).
(参考数据:,, .结果保留一位小数)
【自主解答】
解:如图,过点作,交于点 .
是 的中点,
.
由题意得: ,
,
.
在中, ,
.
.
折叠资料架的高约为 .
类型3 圆模型
【解题策略】对于“圆模型”问题,题中一般会提供几何图形,解题过程中要侧
重于对几何图形本身的分析,通过作辅助线,利用圆的几何性质以及解直角三角形
的知识求解.
例3 某品牌太阳能热水器的实物图和横断面示意
图如图所示.已知真空集热管与支架 所在直
线相交于点,且,支架 与水平地面
垂直., ,
(1) 求支架的长和点 到地面的距离;
,另一支架与水平线的夹角 .
. .
. .
(2) 求热水器容器的侧面圆的半径 的长.
结果精确到.参考数据:,, ,
【自主解答】
(1) 求支架的长和点 到地面的距离;
解:如图,过点作,垂足为 .
, ,
.
, ,
.
支架的长约为,点到地面的距离为 .
(2) 求热水器容器的侧面圆的半径 的长.
结果精确到.参考数据:,, ,
【自主解答】
解:设 ,
.
, .
.
在中, ,
.
,解得 .
.
类型1 三角形模型
1.[2024·辽宁] 如图1,在水平地面上,一辆小车
用一根绕过定滑轮的绳子将物体竖直向上提
起.起始位置示意图如图2,此时测得点到
所在直线的距离, ;停止位
(1) 求 的长;
置示意图如图3,此时测得 (点,,在同一直线上,且直线 与
地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子
总长不变.
. .
. .
(2) 求物体上升的高度结果精确到 .
参考数据:,,,
(1) 求 的长;
解:在 中,
, ,
.
.
(2) 求物体上升的高度结果精确到 .
参考数据:,,,
解:在中,, ,
根据勾股定理得:
.
在中, ,
,即 ,
.
,
.
故物体上升的高度约为 .
2.屏风,是中国传统建筑物内部挡风用的一种家
具,也是一种装饰物.图1是一个四扇屏风,它能
够在室内为后面休息的人提供遮挡,它的俯视图
如图2所示,其中 ,
(1) 当 时,________ ;
(2) 若需要的长度为,应该将 的值调整为多少? 参考数据:
,,
点,,在同一条直线上, 的长为该屏风能够遮挡的长度,若
, 的值可以根据屏风不同的摆放方式而改变.
(1) 当 时,_____ ;
120
(2) 若需要的长度为,应该将 的
值调整为多少?参考数据: ,
,
解:如图,分别过点,作于点, 于
点 .
, ,
.
.
.
.
应该将 的值调整为 .
3.综合与实践
素材一:图1是某款遮阳棚,图2、图3是它的
侧面示意图,点, 为墙壁上的固定点,摇臂
绕点旋转过程中长度保持不变,遮阳棚
素材二:该地区某天不同时刻太阳光线与地面的夹角 的正切值如下.
时刻/时 12 13 14 15
角 的正切值 5 2.5 1.25 1
可自由伸缩,棚面始终保持平整, .
【问题解决】
(1) 如图2,当 时,这天12时
在点 位置摆放的绿萝刚好不被阳光照射到,
则绿萝摆放位置与墙壁的距离为________ ;
(2) 如图3,旋转摇臂,使得点离墙壁的距离为 ,为使绿萝在这天
时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?
(1) 如图2,当 时,这天12时在点 位置摆放的绿萝刚好不被阳光照
射到,则绿萝摆放位置与墙壁的距离为____ ;
1.2
(2) 如图3,旋转摇臂,使得点离墙壁的距离为 ,为使绿萝在这天
时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?
解:过点作于点,于点,则 ,
.
.
由表格可知,在 时,
角 的正切值逐渐减小,即 逐渐减小,
当14时,点 最靠近墙壁,
此时 的长度就是绿萝摆放位置与墙壁的最远距离.
在中,,即, .
.
答:绿萝摆放位置与墙壁的最远距离是 .
类型2 四边形模型
4.[2024·九江柴桑区二模] 某市要新建一座红色文化雕塑,图1是效果图,图2是雕塑
正面的大致示意图,在底座中,, ,
,雕塑主体是五边形,, ,
, , , .
(1) 的度数为________.
(2) 求点到地面的距离. 参考数据:
, ,
,
. .
. .
(1) 的度数为_____.
(2) 求点到地面的距离. 参考数据:
, ,
,
解:过点作于点,过点作于点,交 于
点,过点作于点,作于点,则 .
易知四边形和四边形 是矩形,
, .
在 中,
.
在 中,
.
, .
.
在中, .
.
故点到地面的距离约为 .
5.某数学小组用五个全等的菱形在同一平面
内拼成了一个轴对称的无人机模型,图1是
无人机模型的示意图,其中,,, 四
点在同一条直线上,菱形的边长为 .
(1) 若,,,四点在同一条直线上, ,则此时无人机模型的宽
度 ________ .
(2) 如图2,当无人机模型中的菱形被调整为正方形时,无人机模型的宽度相比
(1)中增加了多少?
结果精确到,,,, ,
,,
(1) 若,,,四点在同一条直线上, ,则此时无人机模型的宽
度 ____ .
47
(2) 如图2,当无人机模型中的菱形被调整为正方形时,无人机模型的宽度相比
(1)中增加了多少?
结果精确到,,,, ,
,,
解:当无人机模型中的菱形被调整为正方形时,如图,
过点作.由题意可知 为等腰直角三角
形,
.
, .
连接.由题意可知 ,
,
.
过点作于点,易得 .
无人机模型的宽度 .
相比(1),无人机模型的宽度增加了
.
6.某景区草地上竖立着一个如图1所示的雕塑,现
将其中两个近似大小相同的矩形框架抽象成如图2
所示的图形,矩形可由矩形绕点 旋转
得到,点在上,延长交于点.连接 ,
.
(1) 判断四边形 的形状并给予证明;
(2) 若点在水平地面上,与水平地面平行, , ,
,求点到水平地面的距离.结果精确到
参考数据:,,, ,
(1) 判断四边形 的形状并给予证明;
解:四边形 是平行四边形.
证明: 四边形 是矩形,
,, .
.
四边形是矩形, .
结合旋转易得 ,
.
由旋转得, .
又, 四边形 为平行四边形.
(2) 若点在水平地面上,与水平地面平行, , ,
,求点到水平地面的距离.结果精确到
参考数据:,,, ,
解:如图,延长交水平地面于点,连接 .
,, .
.
.
由(1)易知,.又 ,
.
由平行线的性质易知 ,
.
,
即点到水平地面的距离约为 .
类型3 圆模型
7.图1所示的是一种纸巾盒,由盒身和圆弧盖组成,
通过圆弧盖的旋转来开关纸巾盒.图2是其侧面简
化示意图,已知矩形的长 ,宽
(1) 求所在的的半径长及 所对的圆心角度数;
(2) 如图3,将圆弧盖板侧面从起始位置绕点旋转 ,求 在这个旋
转过程中扫过的面积.
参考数据:,. 取
,圆弧盖板侧面所在圆的圆心是矩形的中心,绕点 旋转开
关(所有结果保留小数点后一位).
. .
. .
(1) 求所在的的半径长及 所对的圆心角度数;
解:如图,连接,,相交于点,为矩形 的中心.
四边形 为矩形,
.
在 中,
.
的半径长 .
,
.
.
(2) 如图3,将圆弧盖板侧面 从起始位置
绕点旋转 ,求 在这个旋转过程中
扫过的面积.
解:如图, ,
扫过的面积 .
参考数据: ,
. 取
8.“南昌之星”摩天轮,是国内最高的摩天轮,位
于江西省南昌市红谷滩区红角洲赣江市民公园.
游客乘坐南昌之星摩天轮可以从高处俯瞰四周美
(1) 若摩天轮转动一周约 ,则摩天轮每分钟转________度.
(2) 若 ,则点 距离地面多少米?
(3) 游客甲从点 进入座舱之后,又有8个座舱经过,游客乙进入第8个座舱,当
甲、乙乘坐的座舱到地面的距离相等时,求他们的座舱距离地面的高度.
参考数据:,,,
景,饱览赣江两岸风光.据工作人员介绍,该摩天轮总高度为 ,转盘直径为
,设有60个座舱,游客先乘坐直升电梯到入口(入口在摩天轮距地面 的最低
点处)处等待,当座舱到达最低点 处时有序进入座舱. (结果保留小数点后一位)
(1) 若摩天轮转动一周约 ,则摩天轮每分钟转____度.
12
(2) 若 ,则点 距离地面多少米?
解:如答图1,过点作于点,过点作于点 .
,, ,
.
四边形 为矩形.
.
又 , ,
.
.
.
答:点距离地面约 .
(3) 游客甲从点 进入座舱之后,又有8个座舱经过,游客乙进入第8个座舱,当
甲、乙乘坐的座舱到地面的距离相等时,求他们的座舱距离地面的高度.
参考数据:,,,
解: 摩天轮一共有60个座舱且旋转一周为 ,
每两个座舱相隔 .
设甲乘坐的座舱为点,乙乘坐的座舱为点 ,
由题意得甲、乙两人的座舱形成的夹角 .
甲、乙两人座舱到地面的距离相等,
.
延长交于点 ,
则 .
如答图2,过点作,垂足为,过点作于点 ,
易知四边形 为矩形.
.
, .
.
.
答:甲、乙乘坐的座舱距离地面的高度约为 .
同课章节目录
