沪科版七下(2024版)10.3 平行线的性质 课件
文档属性
| 名称 | 沪科版七下(2024版)10.3 平行线的性质 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 09:31:04 | ||
图片预览






文档简介
(共32张PPT)
第10章 相交线、平行线与平移
10.3 平行线的性质
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解并掌握平行线的三条性质,能运用性质进行角的计算和简单推理,规范书写推理过程。
01
通过类比、推理、验证等活动,发展空间观念和逻辑推理能力,体会“由因导果”的推理方法,感悟性质与判定的互逆关系。
02
感受几何知识的系统性和逻辑美,培养严谨的数学思维和合作探究精神,体会数学在生活中的应用价值。
03
02
新知导入
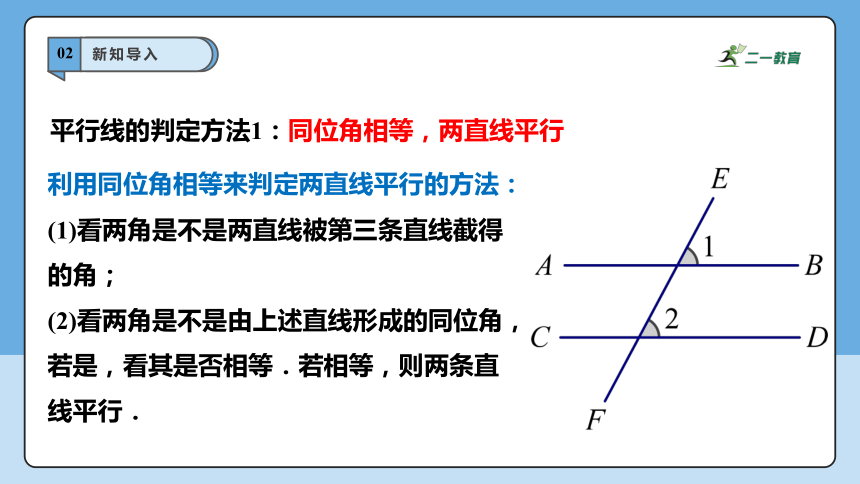
利用同位角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的同位角,若是,看其是否相等.若相等,则两条直线平行.
平行线的判定方法1:同位角相等,两直线平行
02
新知导入
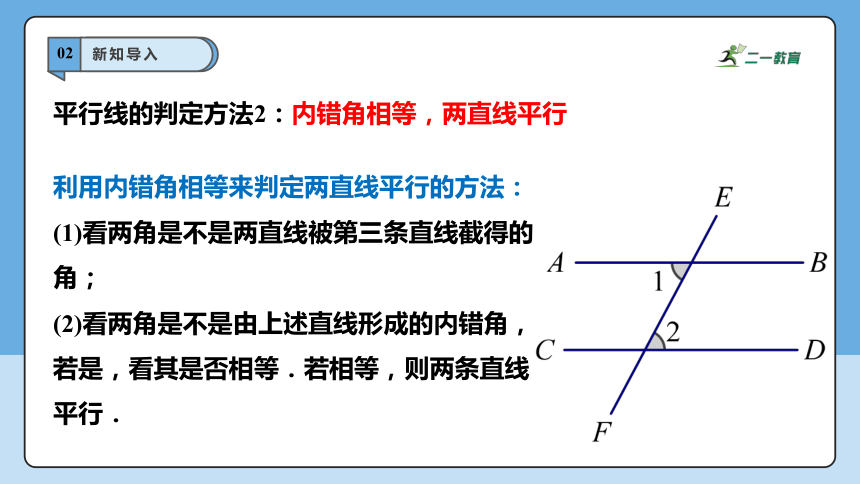
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
平行线的判定方法2:内错角相等,两直线平行
02
新知导入
平行线的判定方法3:同旁内角互补,两直线平行.
利用同旁内角互补来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的同旁内角,若是,看其是否互补.若互补,则两条直线平行.
观察
如图,练习本上的横线都是相互平行的,从中任选两条分别记为AB,CD;画一条直线EF分别与AB,CD相交得8个角.
(1)任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?
(2)再任选一对同位角(如∠2与∠6),量一量它们的度数,它们的大小有什么关系?
由此你能得到什么结论?
03
新知探究
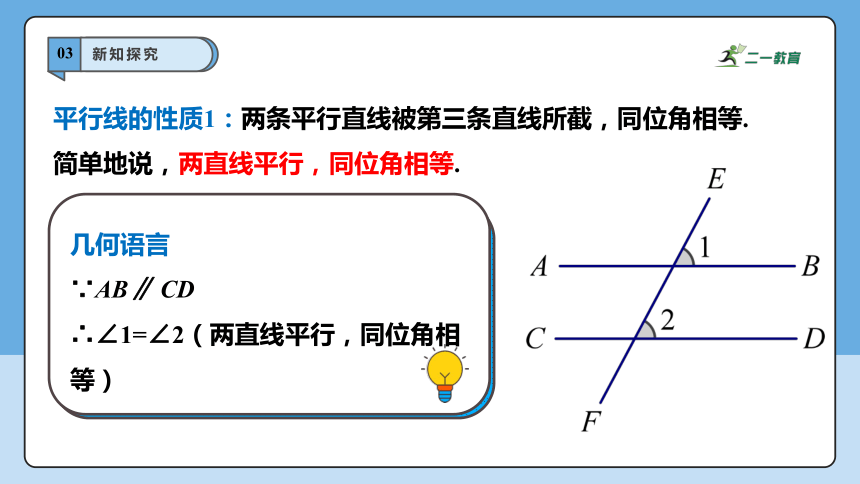
平行线的性质1:两条平行直线被第三条直线所截,同位角相等.
简单地说,两直线平行,同位角相等.
几何语言
∵AB∥ CD
∴∠1=∠2(两直线平行,同位角相等)
03
新知探究
探究:在下图中,当AB∥ CD时,内错角∠3与∠5的大小有什么关系?同旁内角∠4与∠5之间又有什么关系?
猜测:∠3=∠5
∠4+∠5=180°
你能说明理由吗?
03
新知探究
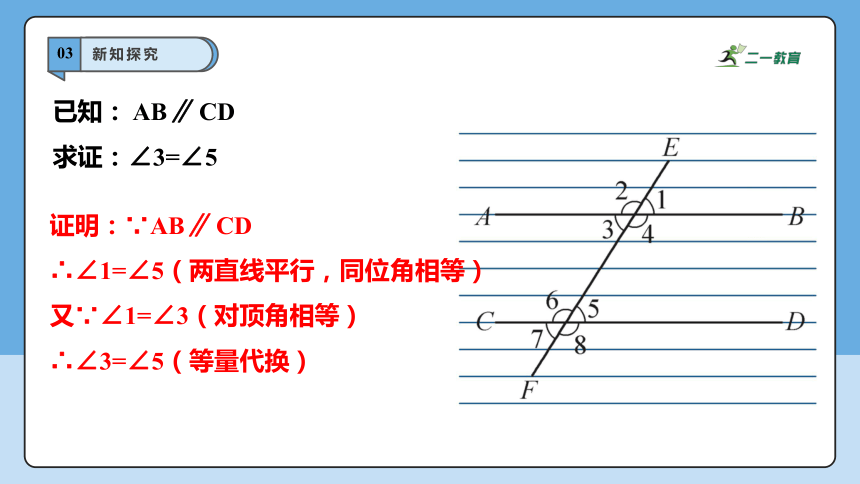
已知: AB∥ CD
求证:∠3=∠5
证明:∵AB∥ CD
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1=∠3(对顶角相等)
∴∠3=∠5(等量代换)
03
新知探究
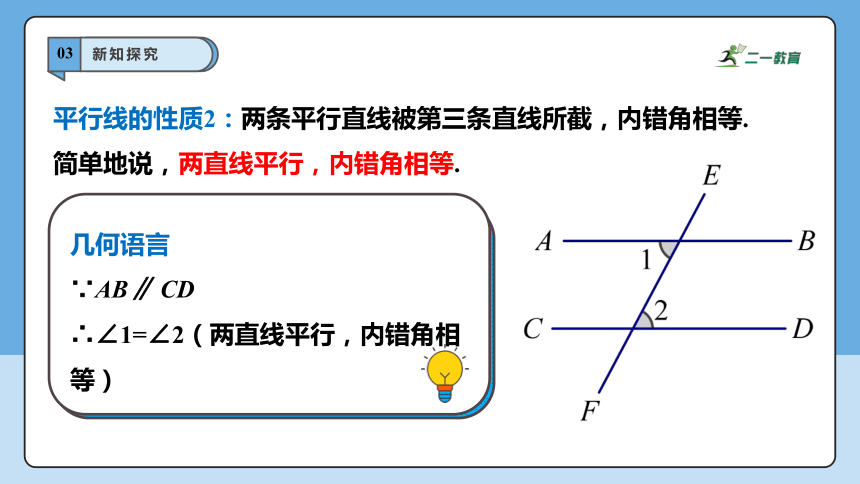
平行线的性质2:两条平行直线被第三条直线所截,内错角相等.
简单地说,两直线平行,内错角相等.
几何语言
∵AB∥ CD
∴∠1=∠2(两直线平行,内错角相等)
03
新知探究
已知: AB∥ CD
求证:∠4+∠5=180°
证明:∵AB∥ CD
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1+∠4=180°
∴∠4+∠5=180°
性质1
03
新知探究
已知: AB∥ CD
求证:∠4+∠5=180°
证明:∵AB∥ CD
∴∠3=∠5(两直线平行,内错角相等)
又∵∠3+∠4=180°
∴∠4+∠5=180°
性质2
03
新知探究
平行线的性质3:两条平行直线被第三条直线所截,同旁内角互补.
简单地说,两直线平行,同旁内角互补.
几何语言
∵AB∥ CD
∴∠1=∠2(两直线平行,同旁内角互补)
03
新知探究
例1
如图,已知点D,E,F分别在△ABC的边AB,AC,BC上,
解:(1)因为DE∥ BC,
所以∠ADE=∠B=48°.
且DE∥ BC,∠B=48°.
(1)试求∠ADE的度数;
(2)若FD是∠BFE的平分线,且EF∥ AB,求∠EDF的度数.
03
新知探究
解:(2)因为FD平分∠BFE,所以∠BFD=∠EFD=∠BFE.
由EF∥ AB,得∠B+∠BFE=180°,
且∠BFD=∠BFE,即∠B+2∠BFD=180°.
因为∠B=48°,所以∠BFD=66°.
因为DE∥ BC,所以∠EDF=∠BFD=66°.
04
课堂练习
【知识技能类作业】必做题:
1.下列命题中,是真命题的为( )
A.两条直线被第三条直线所截,内错角相等
B.垂线段最短
C.过一点有且只有一条直线与已知直线垂直
D.垂直于同一直线的两直线平行
B
04
课堂练习
【知识技能类作业】必做题:
2.如图,AB∥ CD,若∠1=52°,∠2=120°,则∠3的度数为( )
A.68°
B.60°
C.52°
D.48°
A
04
课堂练习
【知识技能类作业】必做题:
3.如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=54°,则∠2的度数为( )
A.36°
B.40°
C.46°
D.50°
A
04
课堂练习
【知识技能类作业】选做题:
4.将一张长方形纸片按如图方式折叠,若∠1=70°,则∠2= °.
40
04
课堂练习
【知识技能类作业】选做题:
5.如图,点A在直线DE上,则∠BAC的度数为 时,DE∥ BC.
46°
04
课堂练习
【知识技能类作业】选做题:
6.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是100°,第二次拐的角∠B是130°,第三次拐的角是∠C,这时恰好和第一次拐弯之前的道路平行,则∠C的度数是 .
150°
04
课堂练习
【综合拓展类作业】
7.如图,直线AB,CD被直线EF所截,AB∥ CD,∠1=100°,试求∠3的度数.
解:因为AB∥ CD,
所以∠1=∠2=100°(两直线平行,同位角相等).
又因为∠2+∠3=180°,
所以∠3=180°∠2=180°100°=80°.
05
课堂小结
平行线的性质1:两条平行直线被第三条直线所截,同位角相等.
简单地说,两直线平行,同位角相等.
平行线的性质2:两条平行直线被第三条直线所截,内错角相等.
简单地说,两直线平行,内错角相等.
平行线的性质3:两条平行直线被第三条直线所截,同旁内角互补.
简单地说,两直线平行,同旁内角互补.
06
作业布置
【知识技能类作业】
1.如图,CD∥ AB,点O在AB上,OF平分∠AOD,OF⊥OE,∠D=130°,则∠BOE的度数为( )
A.65°
B.50°
C.30°
D.25°
A
06
作业布置
【知识技能类作业】
2.如图,直线a∥ b,∠A=38°,∠1=46°,则∠2的度数是( )
A.84°
B.96°
C.104°
D.106°
A
06
作业布置
【知识技能类作业】
3.如图,将含30°角的直角三角板与直尺按如图所示的方式放置.若∠1=80°,则∠2的度数为( )
A.80°
B.60°
C.40°
D.20°
C
06
作业布置
【综合拓展类作业】
4.如图,∠DFE=72°,∠2=36°,P是BC上一点且FP平分∠BFC.
(1)请判断FP与EC的位置关系,并说明理由.
(2)若∠1=2∠2,∠D=121°,求∠A的度数.
(1)解:FP∥ EC,理由如下,
∵∠DFE=72°,∴∠BFC=∠DFE=72°,
∵FP平分∠BFC,∴∠PFC=∠BFC= ×72°=36°,
又∵∠2=36°,∴∠PFC=∠2,∴FP∥ EC.
06
作业布置
(2)解:∵∠1=2∠2,∠2=36°,
∴∠1=2×36°=72°,
∵∠DFE=72°,
∴∠DFE=∠1,
∴DF∥ AB,
又∵∠D=121°,
∴∠A=180°∠D=180°121°=59°.
07
板书设计
性质1:
性质2:
性质3:
10.3 平行线的性质
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第10章 相交线、平行线与平移
10.3 平行线的性质
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
理解并掌握平行线的三条性质,能运用性质进行角的计算和简单推理,规范书写推理过程。
01
通过类比、推理、验证等活动,发展空间观念和逻辑推理能力,体会“由因导果”的推理方法,感悟性质与判定的互逆关系。
02
感受几何知识的系统性和逻辑美,培养严谨的数学思维和合作探究精神,体会数学在生活中的应用价值。
03
02
新知导入
利用同位角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的同位角,若是,看其是否相等.若相等,则两条直线平行.
平行线的判定方法1:同位角相等,两直线平行
02
新知导入
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
平行线的判定方法2:内错角相等,两直线平行
02
新知导入
平行线的判定方法3:同旁内角互补,两直线平行.
利用同旁内角互补来判定两直线平行的方法:
(1)看两角是不是两直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的同旁内角,若是,看其是否互补.若互补,则两条直线平行.
观察
如图,练习本上的横线都是相互平行的,从中任选两条分别记为AB,CD;画一条直线EF分别与AB,CD相交得8个角.
(1)任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?
(2)再任选一对同位角(如∠2与∠6),量一量它们的度数,它们的大小有什么关系?
由此你能得到什么结论?
03
新知探究
平行线的性质1:两条平行直线被第三条直线所截,同位角相等.
简单地说,两直线平行,同位角相等.
几何语言
∵AB∥ CD
∴∠1=∠2(两直线平行,同位角相等)
03
新知探究
探究:在下图中,当AB∥ CD时,内错角∠3与∠5的大小有什么关系?同旁内角∠4与∠5之间又有什么关系?
猜测:∠3=∠5
∠4+∠5=180°
你能说明理由吗?
03
新知探究
已知: AB∥ CD
求证:∠3=∠5
证明:∵AB∥ CD
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1=∠3(对顶角相等)
∴∠3=∠5(等量代换)
03
新知探究
平行线的性质2:两条平行直线被第三条直线所截,内错角相等.
简单地说,两直线平行,内错角相等.
几何语言
∵AB∥ CD
∴∠1=∠2(两直线平行,内错角相等)
03
新知探究
已知: AB∥ CD
求证:∠4+∠5=180°
证明:∵AB∥ CD
∴∠1=∠5(两直线平行,同位角相等)
又∵∠1+∠4=180°
∴∠4+∠5=180°
性质1
03
新知探究
已知: AB∥ CD
求证:∠4+∠5=180°
证明:∵AB∥ CD
∴∠3=∠5(两直线平行,内错角相等)
又∵∠3+∠4=180°
∴∠4+∠5=180°
性质2
03
新知探究
平行线的性质3:两条平行直线被第三条直线所截,同旁内角互补.
简单地说,两直线平行,同旁内角互补.
几何语言
∵AB∥ CD
∴∠1=∠2(两直线平行,同旁内角互补)
03
新知探究
例1
如图,已知点D,E,F分别在△ABC的边AB,AC,BC上,
解:(1)因为DE∥ BC,
所以∠ADE=∠B=48°.
且DE∥ BC,∠B=48°.
(1)试求∠ADE的度数;
(2)若FD是∠BFE的平分线,且EF∥ AB,求∠EDF的度数.
03
新知探究
解:(2)因为FD平分∠BFE,所以∠BFD=∠EFD=∠BFE.
由EF∥ AB,得∠B+∠BFE=180°,
且∠BFD=∠BFE,即∠B+2∠BFD=180°.
因为∠B=48°,所以∠BFD=66°.
因为DE∥ BC,所以∠EDF=∠BFD=66°.
04
课堂练习
【知识技能类作业】必做题:
1.下列命题中,是真命题的为( )
A.两条直线被第三条直线所截,内错角相等
B.垂线段最短
C.过一点有且只有一条直线与已知直线垂直
D.垂直于同一直线的两直线平行
B
04
课堂练习
【知识技能类作业】必做题:
2.如图,AB∥ CD,若∠1=52°,∠2=120°,则∠3的度数为( )
A.68°
B.60°
C.52°
D.48°
A
04
课堂练习
【知识技能类作业】必做题:
3.如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=54°,则∠2的度数为( )
A.36°
B.40°
C.46°
D.50°
A
04
课堂练习
【知识技能类作业】选做题:
4.将一张长方形纸片按如图方式折叠,若∠1=70°,则∠2= °.
40
04
课堂练习
【知识技能类作业】选做题:
5.如图,点A在直线DE上,则∠BAC的度数为 时,DE∥ BC.
46°
04
课堂练习
【知识技能类作业】选做题:
6.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是100°,第二次拐的角∠B是130°,第三次拐的角是∠C,这时恰好和第一次拐弯之前的道路平行,则∠C的度数是 .
150°
04
课堂练习
【综合拓展类作业】
7.如图,直线AB,CD被直线EF所截,AB∥ CD,∠1=100°,试求∠3的度数.
解:因为AB∥ CD,
所以∠1=∠2=100°(两直线平行,同位角相等).
又因为∠2+∠3=180°,
所以∠3=180°∠2=180°100°=80°.
05
课堂小结
平行线的性质1:两条平行直线被第三条直线所截,同位角相等.
简单地说,两直线平行,同位角相等.
平行线的性质2:两条平行直线被第三条直线所截,内错角相等.
简单地说,两直线平行,内错角相等.
平行线的性质3:两条平行直线被第三条直线所截,同旁内角互补.
简单地说,两直线平行,同旁内角互补.
06
作业布置
【知识技能类作业】
1.如图,CD∥ AB,点O在AB上,OF平分∠AOD,OF⊥OE,∠D=130°,则∠BOE的度数为( )
A.65°
B.50°
C.30°
D.25°
A
06
作业布置
【知识技能类作业】
2.如图,直线a∥ b,∠A=38°,∠1=46°,则∠2的度数是( )
A.84°
B.96°
C.104°
D.106°
A
06
作业布置
【知识技能类作业】
3.如图,将含30°角的直角三角板与直尺按如图所示的方式放置.若∠1=80°,则∠2的度数为( )
A.80°
B.60°
C.40°
D.20°
C
06
作业布置
【综合拓展类作业】
4.如图,∠DFE=72°,∠2=36°,P是BC上一点且FP平分∠BFC.
(1)请判断FP与EC的位置关系,并说明理由.
(2)若∠1=2∠2,∠D=121°,求∠A的度数.
(1)解:FP∥ EC,理由如下,
∵∠DFE=72°,∴∠BFC=∠DFE=72°,
∵FP平分∠BFC,∴∠PFC=∠BFC= ×72°=36°,
又∵∠2=36°,∴∠PFC=∠2,∴FP∥ EC.
06
作业布置
(2)解:∵∠1=2∠2,∠2=36°,
∴∠1=2×36°=72°,
∵∠DFE=72°,
∴∠DFE=∠1,
∴DF∥ AB,
又∵∠D=121°,
∴∠A=180°∠D=180°121°=59°.
07
板书设计
性质1:
性质2:
性质3:
10.3 平行线的性质
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
