2024-2025学年北师大版九年级数学下册课件3.4课时1 圆周角定理及其推论1(共32张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册课件3.4课时1 圆周角定理及其推论1(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1020.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 08:52:55 | ||
图片预览









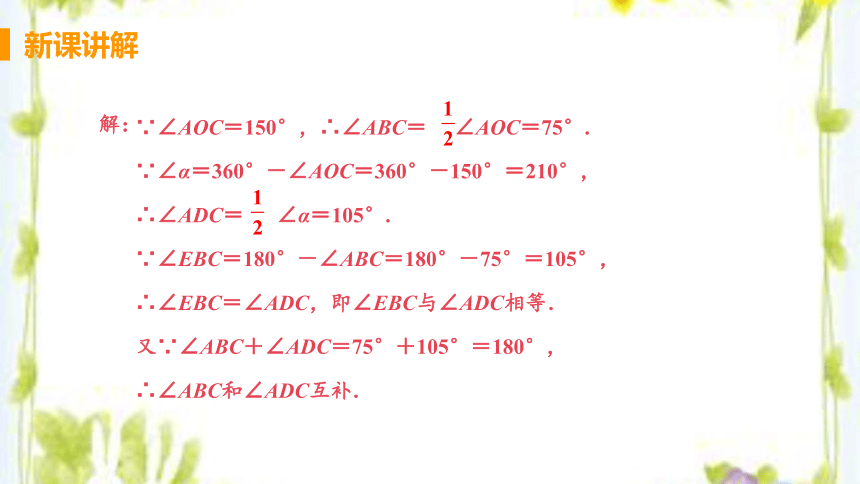
文档简介
(共32张PPT)
第三章 圆
3.4 圆周角和圆心角的关系
课时1 圆周角定理及其推论1
1.圆周角的定义
2.圆周角和圆心角的关系
3.圆周角和弧的关系. (重点、难点)
学习目标
新课导入
什么是圆心角?它具有哪些性质?
新课讲解
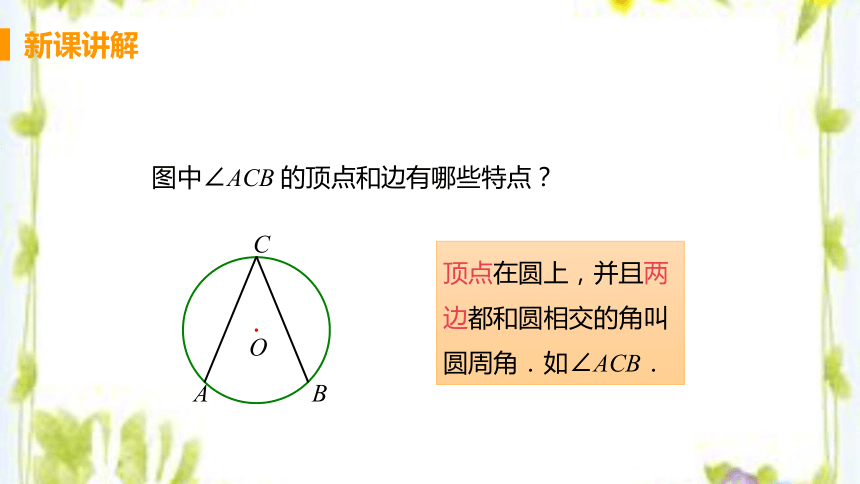
图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
顶点在圆上,并且两
边都和圆相交的角叫
圆周角.如∠ACB.
新课讲解
圆周角的特征:
①角的顶点在圆上;
②角的两边都与圆相交,这两个特征是判定圆周角
不可缺少的条件.
新课讲解
练一练
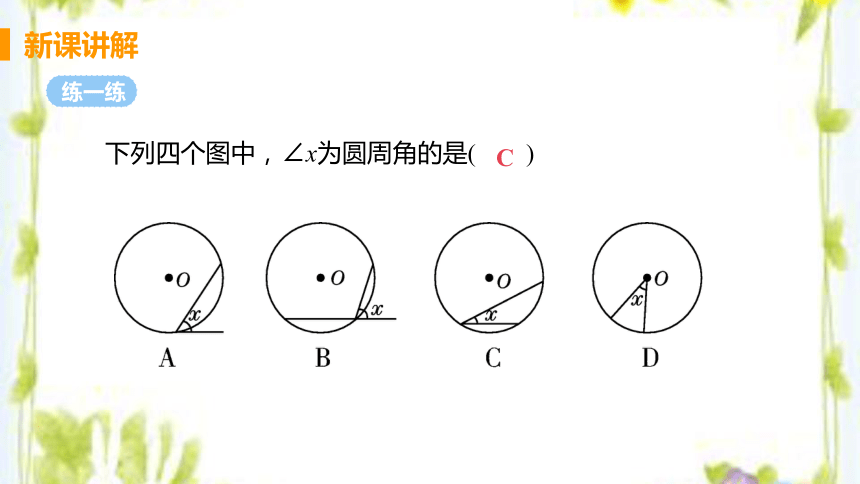
下列四个图中,∠x为圆周角的是( )
C
新课讲解
如图, ∠ AOB = 80°.
(1)请你画出几个 所对的圆周角,这几
个圆周角有什么关系?与同伴进行交流.
(2 )这些圆周角与圆心角∠ AOB的大小有什 么关系?你是
怎样发现的?与同伴进行交流.
在图中,改变∠ AOB的度数,你得到的结论还成立吗?
新课讲解
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
新课讲解
1. 圆周角定理的证明:
已知:如图, ∠ C是 所对的圆 周角, ∠ AOB是
所对的圆心角.
求证: ∠ C= ∠ AOB
分析:根据圆周角和圆心的位置关系,分三种情况讨论:
新课讲解
(1)圆心O在∠ C的一条边上,如图 (1);
(2)圆心O在∠ C的内部,如图 (2);
(3)圆心O在∠ C的外部,如图 (3).
在三种位置关系中,我们选择(1)给出证明,其他情况可以
转化为(1)的情况进行证明.
(1)圆心O在∠ C的一条边上,如图 (1).
∵ ∠ AOB是△AOC的外角,∴ ∠ AOB = ∠ A + ∠ C.
∵ OA = OC,∴ ∠ A = ∠ C.
∴ ∠ AOB = 2 ∠ C,
即 ∠ C = ∠ AOB.
请你完成图 (2)和图 (3)两种情况的证明.
证明:
新课讲解
例
如图,在⊙O中,∠AOC=150°,求∠ABC,∠ADC的度数,并判断∠ABC和∠ADC,∠EBC和∠ADC之间的度数关系.
解题的关键是分清同弧所对的圆心角和圆周角,如
所对的圆心角是∠AOC,所对的圆周角是∠ABC, 所对的圆心角是大于平角的∠α,所对的圆周
角是∠ADC.
分析:
新课讲解
∵∠AOC=150°,∴∠ABC= ∠AOC=75°.
∵∠α=360°-∠AOC=360°-150°=210°,
∴∠ADC= ∠α=105°.
∵∠EBC=180°-∠ABC=180°-75°=105°,
∴∠EBC=∠ADC,即∠EBC与∠ADC相等.
又∵∠ABC+∠ADC=75°+105°=180°,
∴∠ABC和∠ADC互补.
解:
新课讲解
在如图的射门游戏中,当球员在B , D,E处射门
时,所 形成的三个张角∠ ABC, ∠ ADC, ∠ AEC的
大小有什么关系?你能用圆周角定理证明你的结论吗?
新课讲解
练一练
如图,哪个角与∠BAC相等?你还能找到哪些相等的角?
解:∠BDC=∠BAC,如图,
相等的角还有∠ADB=∠ACB,
∠ACD=∠ABD,
∠CAD=∠CBD,
∠1=∠2,∠3=∠4.
课堂小结
(1)一个概念(圆周角);
(2)一个定理:一条弧所对的圆周角等于该弧所对的
圆心角的一半;
(3)一个推论:同圆内,同弧或等弧所对的圆周角相
等. 相等的圆周角所对的弧相等。
当堂小练
1.将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB=________.
25°
当堂小练
2.如图,在⊙O中,AB=BC,点D在⊙O上,∠CDB=25°,则∠AOB=( )
A.45°
B.50°
C.55°
D.60°
B
拓展与延伸
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为( )
A.2 B.4 C.4 D.8
C
A B C D
1.下列各圆中,∠A是圆周角的是( )
A
课后练习
2.(北师9下P79、人教9上P86)如图,当圆心O分别在圆周角∠ABC内部、外部时,求证:∠ABC=AOC.(选一个证明)
证明:当圆心O在圆周角∠ABC内部时,
由知识点2可得∠ABD=AOD,∠CBD=COD,
∴∠ABD+∠CBD=AOD+COD,∴∠ABC=AOC.
当圆心O在圆周角∠ABC外部时,
由知识点2可得∠ABD=AOD,∠CBD=COD,
∴∠CBD-∠ABD=COD-AOD,∴∠ABC=AOC.
3.如图,点A,B,C在圆O上,若∠ACB=36°,则∠AOB= .
72°
4.(人教9上P89)如图,在☉O中,,∠C=75°,则∠A= .
30°
小结:本题求圆心角的解题思路:目标角→对应弧→对应圆周角.
5.(北师9下P80改编)如图,点A,B,P为☉O上的点,若∠PBO=15°,且PA∥OB,则∠AOB= .
30°
小结:本题求圆周角的解题思路:目标角→对应弧→对应圆周角.
6.(人教9上P122)(2024枣庄)如图,在☉O中,弦AB,CD相交于点P,若∠A=30°,∠APD=70°,则∠B=
.
40°
小结:本题的关键是连半径,创造条件利用圆周角定理求解.
7.【例3】如图,在☉O中,∠C=15°,且,则∠E= .
40°
8.(人教9上P124改编)(2024安徽模拟)如图,点A,B,C在圆上,AD,BD分别平分∠BAC和∠ABC,延长AD交该圆于点E,连接BE.求证:BE=DE.
证明:由图可得∠EBC=∠EAC.
∵AD,BD分别平分∠BAC和∠ABC,
∴∠BAE=∠EAC,∠DBC=∠ABD,
∴∠EBC=∠BAE,∴∠EBC+∠DBC=∠BAE+∠ABD.
又∵∠EBC+∠DBC=∠EBD,∠BAE+∠ABD=∠BDE,
∴∠EBD=∠BDE,∴BE=DE.
小结:巧用圆周角定理转化角相等.
9.(北师9下P80、人教9上P88)如图,点A,B,C为☉O上的三个点,∠BOC=2∠AOB,∠BAC=40°,则∠ACB=
.
20°
A.30° B.50° C.60° D.70°
10.如图,在☉O中,两弦AB,CD相交于点E,且AB⊥CD,若∠A=30°,则∠B等于( )
C
11.(创新题)(2023鞍山)如图,AC,BC为☉O的两条弦,D,G分别为AC,BC的中点,☉O的半径为2.若∠C=45°,则DG的长为 .
★12. 0.55 如图,点A,B,C在圆上,△ABC的高AD,BE相交于点H,延长AD交该圆于点G,连接BG.求证:HD=GD.
证明:∵AD,BE是△ABC的高,
∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,
∴∠C=∠AHE,
∵∠AHE=∠BHG,∴∠BHG=∠C,
∵∠C=∠G,∴∠G=∠BHG,∴BH=BG,
又∵AD⊥BC,∴HD=GD.
请完成课本本节对应习题
布置作业
感谢大家欣赏
第三章 圆
3.4 圆周角和圆心角的关系
课时1 圆周角定理及其推论1
1.圆周角的定义
2.圆周角和圆心角的关系
3.圆周角和弧的关系. (重点、难点)
学习目标
新课导入
什么是圆心角?它具有哪些性质?
新课讲解
图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
顶点在圆上,并且两
边都和圆相交的角叫
圆周角.如∠ACB.
新课讲解
圆周角的特征:
①角的顶点在圆上;
②角的两边都与圆相交,这两个特征是判定圆周角
不可缺少的条件.
新课讲解
练一练
下列四个图中,∠x为圆周角的是( )
C
新课讲解
如图, ∠ AOB = 80°.
(1)请你画出几个 所对的圆周角,这几
个圆周角有什么关系?与同伴进行交流.
(2 )这些圆周角与圆心角∠ AOB的大小有什 么关系?你是
怎样发现的?与同伴进行交流.
在图中,改变∠ AOB的度数,你得到的结论还成立吗?
新课讲解
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
新课讲解
1. 圆周角定理的证明:
已知:如图, ∠ C是 所对的圆 周角, ∠ AOB是
所对的圆心角.
求证: ∠ C= ∠ AOB
分析:根据圆周角和圆心的位置关系,分三种情况讨论:
新课讲解
(1)圆心O在∠ C的一条边上,如图 (1);
(2)圆心O在∠ C的内部,如图 (2);
(3)圆心O在∠ C的外部,如图 (3).
在三种位置关系中,我们选择(1)给出证明,其他情况可以
转化为(1)的情况进行证明.
(1)圆心O在∠ C的一条边上,如图 (1).
∵ ∠ AOB是△AOC的外角,∴ ∠ AOB = ∠ A + ∠ C.
∵ OA = OC,∴ ∠ A = ∠ C.
∴ ∠ AOB = 2 ∠ C,
即 ∠ C = ∠ AOB.
请你完成图 (2)和图 (3)两种情况的证明.
证明:
新课讲解
例
如图,在⊙O中,∠AOC=150°,求∠ABC,∠ADC的度数,并判断∠ABC和∠ADC,∠EBC和∠ADC之间的度数关系.
解题的关键是分清同弧所对的圆心角和圆周角,如
所对的圆心角是∠AOC,所对的圆周角是∠ABC, 所对的圆心角是大于平角的∠α,所对的圆周
角是∠ADC.
分析:
新课讲解
∵∠AOC=150°,∴∠ABC= ∠AOC=75°.
∵∠α=360°-∠AOC=360°-150°=210°,
∴∠ADC= ∠α=105°.
∵∠EBC=180°-∠ABC=180°-75°=105°,
∴∠EBC=∠ADC,即∠EBC与∠ADC相等.
又∵∠ABC+∠ADC=75°+105°=180°,
∴∠ABC和∠ADC互补.
解:
新课讲解
在如图的射门游戏中,当球员在B , D,E处射门
时,所 形成的三个张角∠ ABC, ∠ ADC, ∠ AEC的
大小有什么关系?你能用圆周角定理证明你的结论吗?
新课讲解
练一练
如图,哪个角与∠BAC相等?你还能找到哪些相等的角?
解:∠BDC=∠BAC,如图,
相等的角还有∠ADB=∠ACB,
∠ACD=∠ABD,
∠CAD=∠CBD,
∠1=∠2,∠3=∠4.
课堂小结
(1)一个概念(圆周角);
(2)一个定理:一条弧所对的圆周角等于该弧所对的
圆心角的一半;
(3)一个推论:同圆内,同弧或等弧所对的圆周角相
等. 相等的圆周角所对的弧相等。
当堂小练
1.将量角器按如图所示的方式放置在三角形纸板上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB=________.
25°
当堂小练
2.如图,在⊙O中,AB=BC,点D在⊙O上,∠CDB=25°,则∠AOB=( )
A.45°
B.50°
C.55°
D.60°
B
拓展与延伸
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为( )
A.2 B.4 C.4 D.8
C
A B C D
1.下列各圆中,∠A是圆周角的是( )
A
课后练习
2.(北师9下P79、人教9上P86)如图,当圆心O分别在圆周角∠ABC内部、外部时,求证:∠ABC=AOC.(选一个证明)
证明:当圆心O在圆周角∠ABC内部时,
由知识点2可得∠ABD=AOD,∠CBD=COD,
∴∠ABD+∠CBD=AOD+COD,∴∠ABC=AOC.
当圆心O在圆周角∠ABC外部时,
由知识点2可得∠ABD=AOD,∠CBD=COD,
∴∠CBD-∠ABD=COD-AOD,∴∠ABC=AOC.
3.如图,点A,B,C在圆O上,若∠ACB=36°,则∠AOB= .
72°
4.(人教9上P89)如图,在☉O中,,∠C=75°,则∠A= .
30°
小结:本题求圆心角的解题思路:目标角→对应弧→对应圆周角.
5.(北师9下P80改编)如图,点A,B,P为☉O上的点,若∠PBO=15°,且PA∥OB,则∠AOB= .
30°
小结:本题求圆周角的解题思路:目标角→对应弧→对应圆周角.
6.(人教9上P122)(2024枣庄)如图,在☉O中,弦AB,CD相交于点P,若∠A=30°,∠APD=70°,则∠B=
.
40°
小结:本题的关键是连半径,创造条件利用圆周角定理求解.
7.【例3】如图,在☉O中,∠C=15°,且,则∠E= .
40°
8.(人教9上P124改编)(2024安徽模拟)如图,点A,B,C在圆上,AD,BD分别平分∠BAC和∠ABC,延长AD交该圆于点E,连接BE.求证:BE=DE.
证明:由图可得∠EBC=∠EAC.
∵AD,BD分别平分∠BAC和∠ABC,
∴∠BAE=∠EAC,∠DBC=∠ABD,
∴∠EBC=∠BAE,∴∠EBC+∠DBC=∠BAE+∠ABD.
又∵∠EBC+∠DBC=∠EBD,∠BAE+∠ABD=∠BDE,
∴∠EBD=∠BDE,∴BE=DE.
小结:巧用圆周角定理转化角相等.
9.(北师9下P80、人教9上P88)如图,点A,B,C为☉O上的三个点,∠BOC=2∠AOB,∠BAC=40°,则∠ACB=
.
20°
A.30° B.50° C.60° D.70°
10.如图,在☉O中,两弦AB,CD相交于点E,且AB⊥CD,若∠A=30°,则∠B等于( )
C
11.(创新题)(2023鞍山)如图,AC,BC为☉O的两条弦,D,G分别为AC,BC的中点,☉O的半径为2.若∠C=45°,则DG的长为 .
★12. 0.55 如图,点A,B,C在圆上,△ABC的高AD,BE相交于点H,延长AD交该圆于点G,连接BG.求证:HD=GD.
证明:∵AD,BE是△ABC的高,
∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,
∴∠C=∠AHE,
∵∠AHE=∠BHG,∴∠BHG=∠C,
∵∠C=∠G,∴∠G=∠BHG,∴BH=BG,
又∵AD⊥BC,∴HD=GD.
请完成课本本节对应习题
布置作业
感谢大家欣赏
