2025届中考数学预热模拟卷 【云南专用】(含答案)
文档属性
| 名称 | 2025届中考数学预热模拟卷 【云南专用】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-22 08:59:14 | ||
图片预览




文档简介
2025届中考数学预热模拟卷 【云南专用】
【满分100分 考试时间120分钟】
一、选择题(本大题共15小题,每小题2分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.通常把标准大气压下水结冰时的温度规定为,那么比水结冰时的温度低应记作( )
A. B. C. D.
2.据报道,至2月22日,在2025年春运40天里,全社会跨区域人员流动量约为9020000000人次,出行人数再创新高.将9020000000用科学记数法表示应为( )
A. B. C. D.
3.下列运算不正确的是( )
A. B. C. D.
4.点关于原点对称点的坐标为( )
A. B. C. D.
5.由5个相同的小正方体组成的几何体,如图所示,该几何体的主视图是( )
A. B. C. D.
6.甲、乙、丙、丁四种小麦的平均苗高都是,方差分别是,,,,则小麦长势最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.体育精神就是健康向上、不懈奋斗的精神,下列关于体育运动的图标中是轴对称图形的是( )
A. B. C. D.
8.若反比例函数的图象经过点,则k的值为( )
A.8 B. C. D.
9.如图,,,平分,则的度数等于( )
A. B. C. D.
10.按一定规律排列的多项式:,,,,,第n个多项式是( )
A. B.
C. D.
11.估算的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
12.《九章算术》是我国传统数学的重要著作之一,奠定了我国传统数学的基本框架.《九章算术》中记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”大意:有一形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,问它的高与宽各是多少?利用方程思想,设矩形门高为尺,则依题意所列方程为(1丈尺,1尺寸)( )
A. B.
C. D.
13.如图,在平面直角坐标系中,点A的坐标分别为,以原点O为位似中心,把缩小为原来的,则点A的对应点的坐标为( )
A.或 B.
C.或 D.
14.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12m B.13m C.16m D.17m
15.如图,从一块半径为的圆形铁皮上剪出一个圆心角是的扇形,则扇形中弧的长为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题2分,共8分.请把答案填在题中横线上)
16.因式分解:_______.
17.若关于x的一元二次方程有两个相等的实数根,则实数a的值为______.
18.一个多边形的内角和为,这个多边形的边数是________.
19.为了解社区岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图,若该社区中岁的居民约8000人,请根据图中信息估算其中岁的人群中最喜欢微信支付方式的人数为____________人.
三、解答题(本大题共8小题,共62分.解答应写出必要的文字说明,证明过程或演算步骤)
20.(7分)计算:.
21.(6分)如图,点B,C,D,E在同一直线上,,,.求证:.
22.(7分)口袋公园是城市微更新的一项重要举措,近年太原市充分利用城市的边角地、闲置地“见缝插绿”,让口袋公园成为附近居民休闲的好去处.2024年太原全市范围内(含古交)以新建“街角型和社区型”两种口袋公园为主,其中建设的街角型口袋公园的数量比社区型的数量多13个,一个街角型口袋公园的平均占地面积是一个社区型口袋公园的.已知2024年建设的街角型和社区型口袋公园占地总面积分别是12公顷和10.2公顷,分别求建设一个街角型和一个社区型口袋公园的平均占地面积.
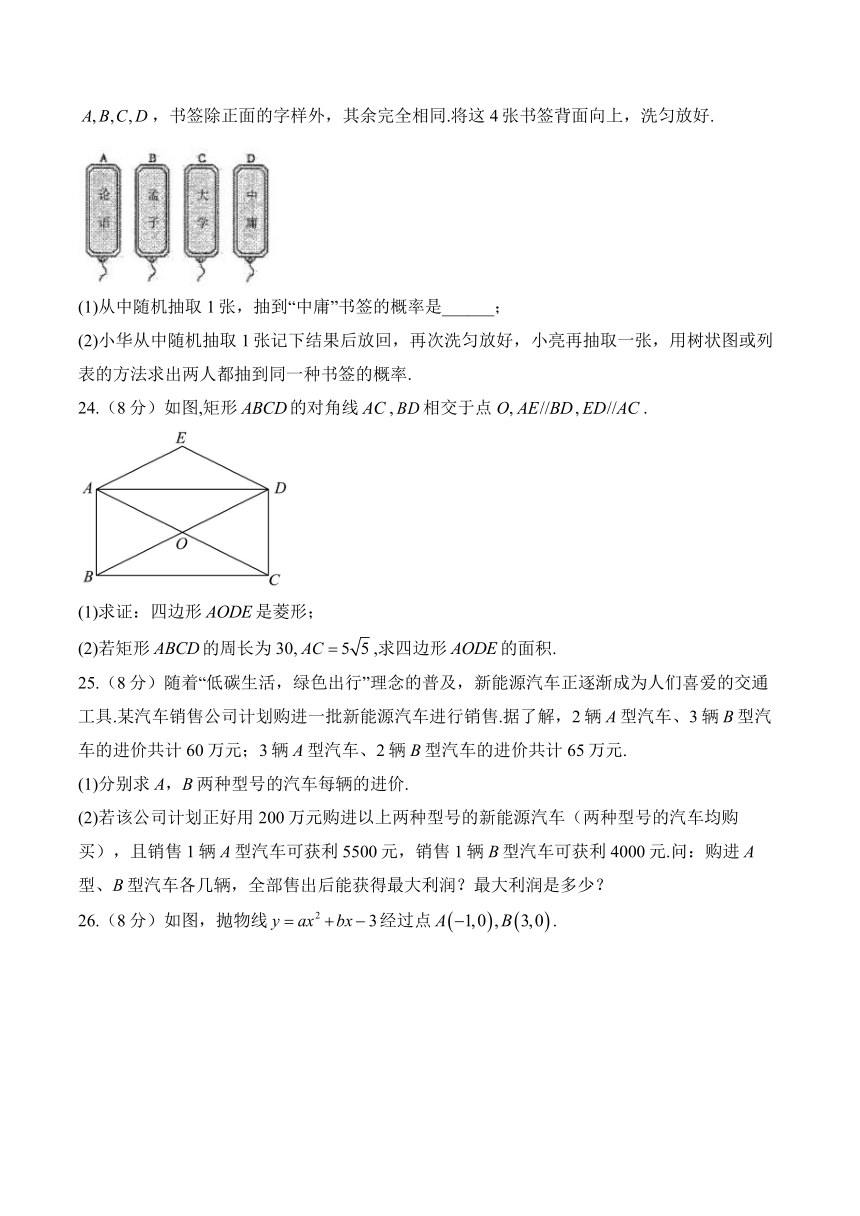
23.(6分)中国古代的“四书”是指《论语》、《孟子》、《大学》和《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分.下面是正面印有“四书”字样的书签,书签除正面的字样外,其余完全相同.将这4张书签背面向上,洗匀放好.
(1)从中随机抽取1张,抽到“中庸”书签的概率是______;
(2)小华从中随机抽取1张记下结果后放回,再次洗匀放好,小亮再抽取一张,用树状图或列表的方法求出两人都抽到同一种书签的概率.
24.(8分)如图,矩形的对角线,相交于点O,,.
(1)求证:四边形是菱形;
(2)若矩形的周长为30,,求四边形的面积.
25.(8分)随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车进行销售.据了解,2辆A型汽车、3辆B型汽车的进价共计60万元;3辆A型汽车、2辆B型汽车的进价共计65万元.
(1)分别求A,B两种型号的汽车每辆的进价.
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),且销售1辆A型汽车可获利5500元,销售1辆B型汽车可获利4000元.问:购进A型、B型汽车各几辆,全部售出后能获得最大利润?最大利润是多少?
26.(8分)如图,抛物线经过点.
(1)求抛物线的解析式;
(2)点在抛物线上,在直线下方的抛物线上是否存在点P,使得的面积最大?若存在,请直接写出面积的最大值和此时点P的坐标;若不存在,请说明理由.
27.(12分)如1图,是的直径,是的弦,点M是外一点,.
(1)求证:与相切.
(2)如2图,连接、,若,与交于点E.
①证明:;
②连接交于点F,连接,若,,求的长.
答案以及解析
1.答案:C
解析:标准大气压下水结冰时的温度规定为,
∴比水结冰时的温度低应记作,
故选:C.
2.答案:B
解析:将9020000000用科学记数法表示应为,
故选:B.
3.答案:B
解析:A.,故该选项正确;
B.,故该选项错误;
C.,故该选项正确;
D.,故该选项正确;
故选:B.
4.答案:D
解析:在平面直角坐标系中关于原点对称的点,其横坐标与纵坐标均互为相反数,
则关于原点对称的点为,
故选:D.
5.答案:B
解析:主视图有3列,每列小正方形数目分别为2,1,1,
∴该几何体的主视图是
故选:B.
6.答案:D
解析:,,,,
,
小麦长势最稳定的是丁,
故选:D.
7.答案:C
解析:选项A、B、D的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项C的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:C.
8.答案:D
解析:∵反比例函数的图象经过点,
∴,
解得,
故选:D.
9.答案:B
解析:∵,
∴,
∴,
∵平分,
∴,
∵,
∴.
故选B.
10.答案:A
解析:∵多项式的x项的次数依次为1,2,3,…,
∴第n个多项式的x项次数为n,
∵多项式的y项的系数依次为1,3,5,…,
∴第n个多项式的y项系数为,
∴第n个多项式为,
故选:A.
11.答案:B
解析:
,
∵,
∴,
∴,
∴,
故选:B.
12.答案:B
解析:设矩形门高为x尺,则矩形门宽为尺,
由题意得,,
故选:B.
13.答案:A
解析:∵以原点O为位似中心,把缩小为原来的,点A的坐标分别为,
∴点A的对应点的坐标为或,即或,
故选:A.
14.答案:D
解析:设旗杆高度为x,则,,,
在中,,即,
解得:,
即旗杆的高度为17米.
故选D.
15.答案:D
解析:连接,过O作交于点D,
∵,
∴,
∵,,
∴,,,
∴,
∴,
∵,,
∴是等边三角形,
∴,
∴,
故选D;
16.答案:/
解析:原式.
故答案为:.
17.答案:
解析:由得,
∵关于x的一元二次方程有两个相等的实数根,
∴,且,
解得.
故答案为.
18.答案:5
解析:设这个多边形的边数为n,
根据多边形内角和定理得,
,
解得.
故答案为:5.
19.答案:1600
解析:本次调查总人数为(人).
∴估算其中岁的人群中最喜欢微信支付方式的人数约为(人).
故答案为:1600.
20.答案:
解析:
.
21.答案:见解析
解析:证明:,
,即,
在和中,
,
,
.
22.答案:建设一个社区型口袋公园的平均占地面积为公顷,则建设街角型口袋公园的平均占地面积为公顷.
解析:设建设一个社区型口袋公园的平均占地面积为公顷,则建设街角型口袋公园的平均占地面积为公顷,则
,
解得:,
经检验:是原方程的根,且符合题意;
∴,
答:建设一个社区型口袋公园的平均占地面积为0.6公顷,则建设街角型口袋公园的平均占地面积为0.4公顷.
23.答案:(1)
(2)
解析:(1)解:由题意知,共有4种等可能的结果,其中抽到“中庸”书签的结果有1种,
∴从中随机抽取1张,抽到“中庸”书签的概率是.
故答案为:.
(2)解:列表如下:
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中两人抽到同一种书签”的结果有4种,
∴概率为.
24.答案:(1)见解析
(2)25
解析:(1)证明:,,
四边形是平行四边形,
矩形,
,
平行四边形是菱形.
(2)矩形,
,,,
矩形的周长为30,
,即,
在中,,
,
,
,
由(1)得,四边形是菱形,
.
四边形的面积为25.
25.答案:(1)每辆A型汽车的进价是15万元,每辆B型汽车的进价是10万元.
(2)购进2辆A型汽车、17辆B型汽车,全部售出后能获得最大利润,最大利润是79000元.
解析:设每辆A型汽车的进价是x万元,每辆B型汽车的进价是y万元,
根据题意,得,
解得,
因此,每辆A型汽车的进价是15万元,每辆B型汽车的进价是10万元;
(2)解析:设该公司购进m辆A型汽车,全部售出后获得的总利润为w元,则该公司购进辆B型汽车,
根据题意,得,即,
,
随m的增大而减小,
又均为正整数,
的最小值为2,
当时,w取得最大值,最大值为(元),
此时(辆).
因此,购进2辆A型汽车、17辆B型汽车,全部售出后能获得最大利润,最大利润是79000元.
26.答案:(1)
(2)面积的最大值是,此时点P的坐标为
解析:把点,代入,得
,
解得,
∴抛物线的解析式为;
(2)解析:∵点在抛物线上,
∴,
∴,
设点P的坐标为,
如图,过点P作于点M,过点E作于点N,则,,,,,
∴
,
∴当时,面积的最大值是,此时点P的坐标为.
27.答案:(1)见解析
(2)①见解析;②
解析:是的直径,
,
,
,
,即,
与相切;
(2)①证明:如图,连接,
,,,
,
,
又,
,即,
,
;
②连接,如图所示:
∵,,
∴,,
∴,,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
即①,
∵,,
∴,
∴,
即②,
∴,
∴,
∵,
∴,
∴,
即,
解得:.
【满分100分 考试时间120分钟】
一、选择题(本大题共15小题,每小题2分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.通常把标准大气压下水结冰时的温度规定为,那么比水结冰时的温度低应记作( )
A. B. C. D.
2.据报道,至2月22日,在2025年春运40天里,全社会跨区域人员流动量约为9020000000人次,出行人数再创新高.将9020000000用科学记数法表示应为( )
A. B. C. D.
3.下列运算不正确的是( )
A. B. C. D.
4.点关于原点对称点的坐标为( )
A. B. C. D.
5.由5个相同的小正方体组成的几何体,如图所示,该几何体的主视图是( )
A. B. C. D.
6.甲、乙、丙、丁四种小麦的平均苗高都是,方差分别是,,,,则小麦长势最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.体育精神就是健康向上、不懈奋斗的精神,下列关于体育运动的图标中是轴对称图形的是( )
A. B. C. D.
8.若反比例函数的图象经过点,则k的值为( )
A.8 B. C. D.
9.如图,,,平分,则的度数等于( )
A. B. C. D.
10.按一定规律排列的多项式:,,,,,第n个多项式是( )
A. B.
C. D.
11.估算的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
12.《九章算术》是我国传统数学的重要著作之一,奠定了我国传统数学的基本框架.《九章算术》中记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”大意:有一形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,问它的高与宽各是多少?利用方程思想,设矩形门高为尺,则依题意所列方程为(1丈尺,1尺寸)( )
A. B.
C. D.
13.如图,在平面直角坐标系中,点A的坐标分别为,以原点O为位似中心,把缩小为原来的,则点A的对应点的坐标为( )
A.或 B.
C.或 D.
14.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12m B.13m C.16m D.17m
15.如图,从一块半径为的圆形铁皮上剪出一个圆心角是的扇形,则扇形中弧的长为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题2分,共8分.请把答案填在题中横线上)
16.因式分解:_______.
17.若关于x的一元二次方程有两个相等的实数根,则实数a的值为______.
18.一个多边形的内角和为,这个多边形的边数是________.
19.为了解社区岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图,若该社区中岁的居民约8000人,请根据图中信息估算其中岁的人群中最喜欢微信支付方式的人数为____________人.
三、解答题(本大题共8小题,共62分.解答应写出必要的文字说明,证明过程或演算步骤)
20.(7分)计算:.
21.(6分)如图,点B,C,D,E在同一直线上,,,.求证:.
22.(7分)口袋公园是城市微更新的一项重要举措,近年太原市充分利用城市的边角地、闲置地“见缝插绿”,让口袋公园成为附近居民休闲的好去处.2024年太原全市范围内(含古交)以新建“街角型和社区型”两种口袋公园为主,其中建设的街角型口袋公园的数量比社区型的数量多13个,一个街角型口袋公园的平均占地面积是一个社区型口袋公园的.已知2024年建设的街角型和社区型口袋公园占地总面积分别是12公顷和10.2公顷,分别求建设一个街角型和一个社区型口袋公园的平均占地面积.
23.(6分)中国古代的“四书”是指《论语》、《孟子》、《大学》和《中庸》,它是儒家思想的核心著作,是中国传统文化的重要组成部分.下面是正面印有“四书”字样的书签,书签除正面的字样外,其余完全相同.将这4张书签背面向上,洗匀放好.
(1)从中随机抽取1张,抽到“中庸”书签的概率是______;
(2)小华从中随机抽取1张记下结果后放回,再次洗匀放好,小亮再抽取一张,用树状图或列表的方法求出两人都抽到同一种书签的概率.
24.(8分)如图,矩形的对角线,相交于点O,,.
(1)求证:四边形是菱形;
(2)若矩形的周长为30,,求四边形的面积.
25.(8分)随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车进行销售.据了解,2辆A型汽车、3辆B型汽车的进价共计60万元;3辆A型汽车、2辆B型汽车的进价共计65万元.
(1)分别求A,B两种型号的汽车每辆的进价.
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),且销售1辆A型汽车可获利5500元,销售1辆B型汽车可获利4000元.问:购进A型、B型汽车各几辆,全部售出后能获得最大利润?最大利润是多少?
26.(8分)如图,抛物线经过点.
(1)求抛物线的解析式;
(2)点在抛物线上,在直线下方的抛物线上是否存在点P,使得的面积最大?若存在,请直接写出面积的最大值和此时点P的坐标;若不存在,请说明理由.
27.(12分)如1图,是的直径,是的弦,点M是外一点,.
(1)求证:与相切.
(2)如2图,连接、,若,与交于点E.
①证明:;
②连接交于点F,连接,若,,求的长.
答案以及解析
1.答案:C
解析:标准大气压下水结冰时的温度规定为,
∴比水结冰时的温度低应记作,
故选:C.
2.答案:B
解析:将9020000000用科学记数法表示应为,
故选:B.
3.答案:B
解析:A.,故该选项正确;
B.,故该选项错误;
C.,故该选项正确;
D.,故该选项正确;
故选:B.
4.答案:D
解析:在平面直角坐标系中关于原点对称的点,其横坐标与纵坐标均互为相反数,
则关于原点对称的点为,
故选:D.
5.答案:B
解析:主视图有3列,每列小正方形数目分别为2,1,1,
∴该几何体的主视图是
故选:B.
6.答案:D
解析:,,,,
,
小麦长势最稳定的是丁,
故选:D.
7.答案:C
解析:选项A、B、D的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项C的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:C.
8.答案:D
解析:∵反比例函数的图象经过点,
∴,
解得,
故选:D.
9.答案:B
解析:∵,
∴,
∴,
∵平分,
∴,
∵,
∴.
故选B.
10.答案:A
解析:∵多项式的x项的次数依次为1,2,3,…,
∴第n个多项式的x项次数为n,
∵多项式的y项的系数依次为1,3,5,…,
∴第n个多项式的y项系数为,
∴第n个多项式为,
故选:A.
11.答案:B
解析:
,
∵,
∴,
∴,
∴,
故选:B.
12.答案:B
解析:设矩形门高为x尺,则矩形门宽为尺,
由题意得,,
故选:B.
13.答案:A
解析:∵以原点O为位似中心,把缩小为原来的,点A的坐标分别为,
∴点A的对应点的坐标为或,即或,
故选:A.
14.答案:D
解析:设旗杆高度为x,则,,,
在中,,即,
解得:,
即旗杆的高度为17米.
故选D.
15.答案:D
解析:连接,过O作交于点D,
∵,
∴,
∵,,
∴,,,
∴,
∴,
∵,,
∴是等边三角形,
∴,
∴,
故选D;
16.答案:/
解析:原式.
故答案为:.
17.答案:
解析:由得,
∵关于x的一元二次方程有两个相等的实数根,
∴,且,
解得.
故答案为.
18.答案:5
解析:设这个多边形的边数为n,
根据多边形内角和定理得,
,
解得.
故答案为:5.
19.答案:1600
解析:本次调查总人数为(人).
∴估算其中岁的人群中最喜欢微信支付方式的人数约为(人).
故答案为:1600.
20.答案:
解析:
.
21.答案:见解析
解析:证明:,
,即,
在和中,
,
,
.
22.答案:建设一个社区型口袋公园的平均占地面积为公顷,则建设街角型口袋公园的平均占地面积为公顷.
解析:设建设一个社区型口袋公园的平均占地面积为公顷,则建设街角型口袋公园的平均占地面积为公顷,则
,
解得:,
经检验:是原方程的根,且符合题意;
∴,
答:建设一个社区型口袋公园的平均占地面积为0.6公顷,则建设街角型口袋公园的平均占地面积为0.4公顷.
23.答案:(1)
(2)
解析:(1)解:由题意知,共有4种等可能的结果,其中抽到“中庸”书签的结果有1种,
∴从中随机抽取1张,抽到“中庸”书签的概率是.
故答案为:.
(2)解:列表如下:
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中两人抽到同一种书签”的结果有4种,
∴概率为.
24.答案:(1)见解析
(2)25
解析:(1)证明:,,
四边形是平行四边形,
矩形,
,
平行四边形是菱形.
(2)矩形,
,,,
矩形的周长为30,
,即,
在中,,
,
,
,
由(1)得,四边形是菱形,
.
四边形的面积为25.
25.答案:(1)每辆A型汽车的进价是15万元,每辆B型汽车的进价是10万元.
(2)购进2辆A型汽车、17辆B型汽车,全部售出后能获得最大利润,最大利润是79000元.
解析:设每辆A型汽车的进价是x万元,每辆B型汽车的进价是y万元,
根据题意,得,
解得,
因此,每辆A型汽车的进价是15万元,每辆B型汽车的进价是10万元;
(2)解析:设该公司购进m辆A型汽车,全部售出后获得的总利润为w元,则该公司购进辆B型汽车,
根据题意,得,即,
,
随m的增大而减小,
又均为正整数,
的最小值为2,
当时,w取得最大值,最大值为(元),
此时(辆).
因此,购进2辆A型汽车、17辆B型汽车,全部售出后能获得最大利润,最大利润是79000元.
26.答案:(1)
(2)面积的最大值是,此时点P的坐标为
解析:把点,代入,得
,
解得,
∴抛物线的解析式为;
(2)解析:∵点在抛物线上,
∴,
∴,
设点P的坐标为,
如图,过点P作于点M,过点E作于点N,则,,,,,
∴
,
∴当时,面积的最大值是,此时点P的坐标为.
27.答案:(1)见解析
(2)①见解析;②
解析:是的直径,
,
,
,
,即,
与相切;
(2)①证明:如图,连接,
,,,
,
,
又,
,即,
,
;
②连接,如图所示:
∵,,
∴,,
∴,,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
即①,
∵,,
∴,
∴,
即②,
∴,
∴,
∵,
∴,
∴,
即,
解得:.
同课章节目录
